Задали функцию на интервале от 0 до 30. Для этого воспользовались скриптом compile-func.py .
Параметры : -g 30,4.5,8+12,5,12.2+10,5.3,16.5+30,4.5,20.3+20,5.5,7
Мы получили файл .txt и изображение полученной функции :
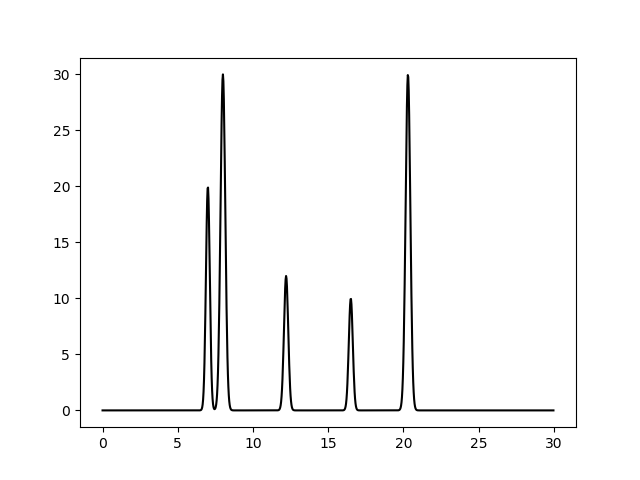
Полученная функция далее была разложена в ряд Фурье с помощью скрипта func2fourier.py. Получили набор из 498 гармоник, где для каждой гармоники рассчитана амплитуда и фаза. Полученные гармоники Фурье фильтровались при помощи скрипта fourier-filter.py, чтобы оставить некоторый ограниченный набор, из которого далее восстанавливалась функция скрпитом fourier2func.py.


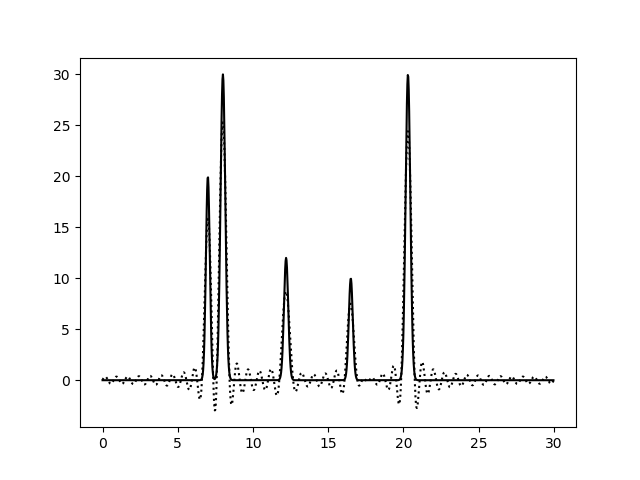

Начиная с n=30 можно сказать что восстановление хорошее, однако отличным его можно назвать при n=50. Внесем шум в набор гармоник 0-40 по амплитудам(F) и фазам(P). Подали func2fourier.py параметры F=30 и P=30. График функции, восстанавливался по гармоникам с 0 по 40.
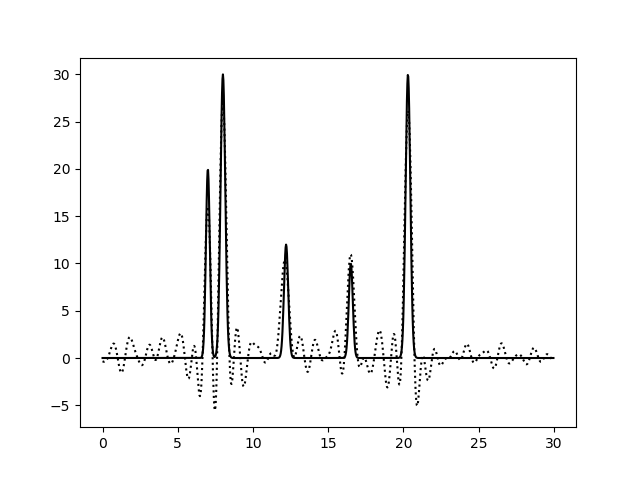
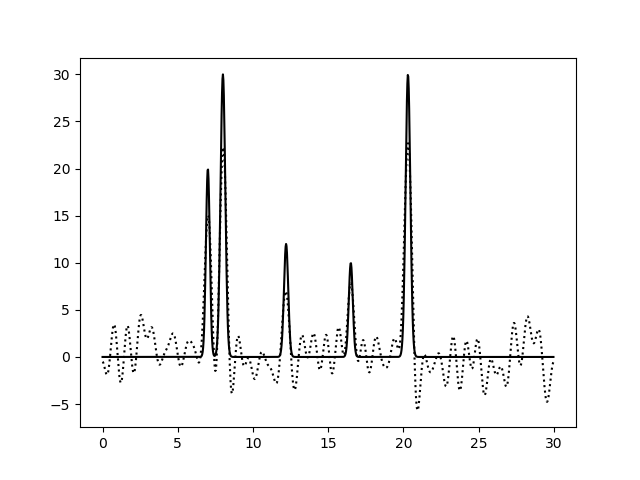
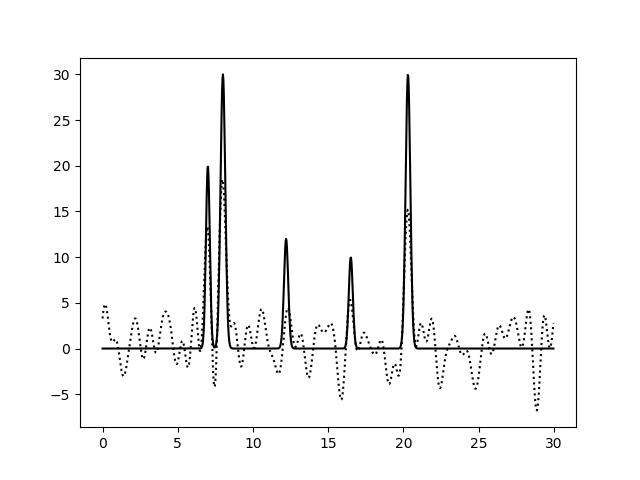
Как изменение амплитуд, так и изменения по фазам приводят усилению шума и к значительному ухудшению качества, однако этого недостаточно что бы помешать правильной интерпретации результатов. Однако комбинированное изменение амплитуды и частоты приводит к значительному ухудшению качества восстановления.
Неполный набор гармоник
Сначала убрала несколько первых гармоник и качество упало. Как оказалось, самые первые гармоники влияют значительно, меняя базовый уровень функции. Гармоники с меньшими периодами (несколько ангстрем) делают пики максимумов плохо различимыми.

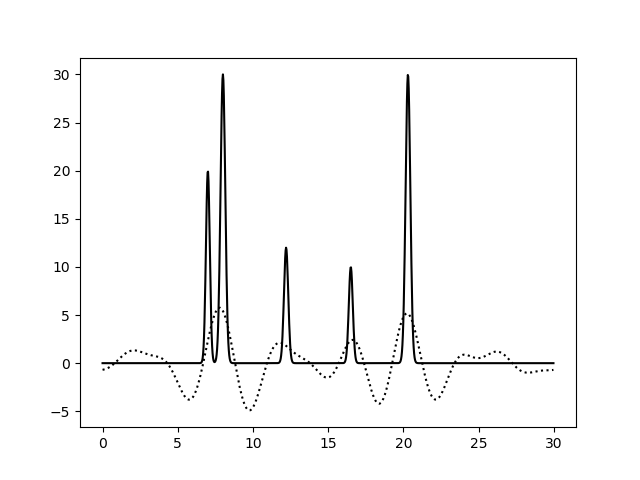
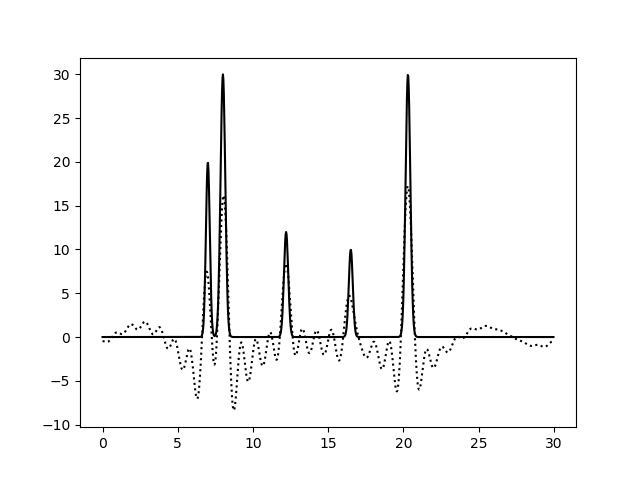

Если убирать гармоники из середины или из конца, качество меняется незначительно.
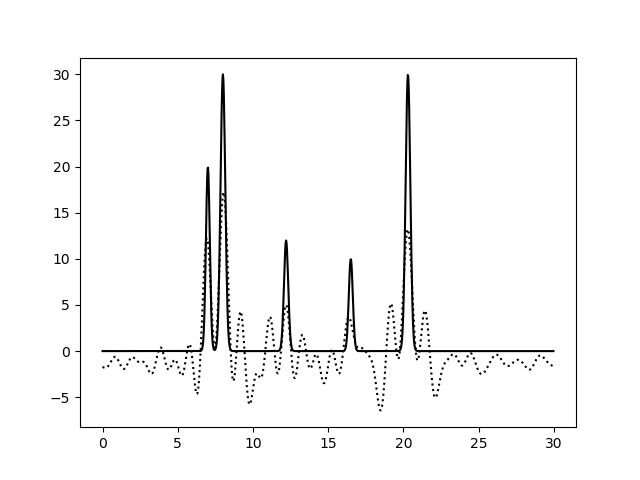

По ссылке можно посмотреть итоговую таблицу оценки качества гармоник. Выводы:
1) При использовании полного набора гармоник точность приближения постепенно увеличивается. 2) Ранние гармоники вносят больший вклад в качество структуры.