Модель для компьютерного эксперимента. На отрезке от 0 до 30 (Å) задается функция,
имеющая вид нескольких гауссовых кривых. Эти кривые, представляющие собой пики на графике,
соответствуюшие электронным плотностям атомов. Максимум электронной плотности в центре
атома приблизительно пропорционален числу электронов в атоме. Атомы в молекуле связаны
ковалентно и находятся на расстоянии 1-1.5 Å друг от друга.
В качестве модельной функции был использован вариант 7.
С помощью команды python compile-func.py
-g 10,2,5+10,2,7+30.0,2,12+30.0,2,16+30.0,2,22+30,2,24 был получен соответствующий
файл.
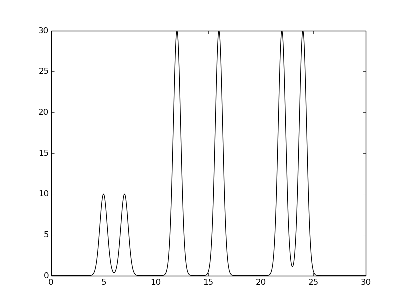
График заданной функции ЭП на отрезке [0, 30] для исследуемой функции.
С помощью команды python func2fourier.py -i func.txt
был получен файл с коэффициентами разложения функции в ряд Фурье.
Далее при помощи скриптов fourier-filter.py и
fourier2func.py были получены данные для полных наборов гармоник.
Ниже приведены графики заданной функции на отрезке [0, 30], а также графики апроксимирующих функций Фурье,
отмеченных пунктиром.
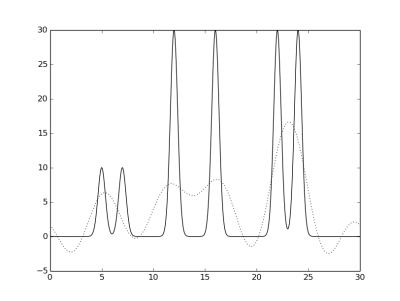
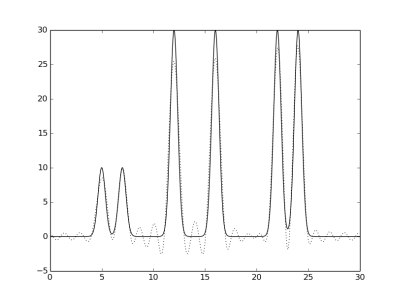

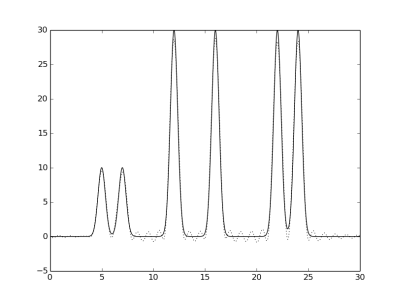
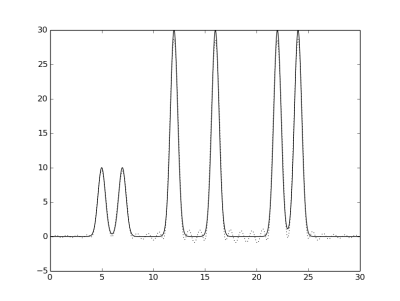
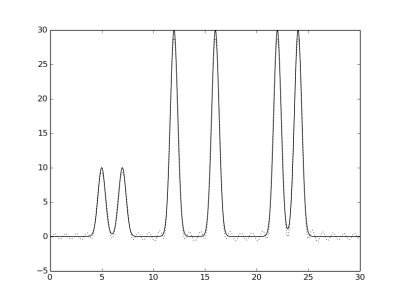
Гармоники 0-5, 0-20, 0-25, 0-27, 0-28, 0-29 и 0-30, соответственно.
Как можно заметить на изображении ниже, несмотря на небольшую волнистость на горизонтальных участках,
восстановление при 30 гармониках уже можно считать очень хорошим, так как
отчетливо различимы все минимумы и максимумы.
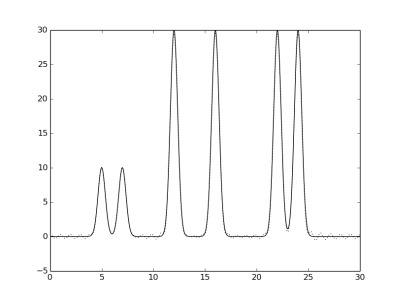
Гаромники 0-30
Восстановление ЭП по набору гармоник (обратное преобразование Фурье) проводилось скриптом
fourier2func.py.
С помощью команд были получены
изображения функций фурье с неполным набором гармоник:
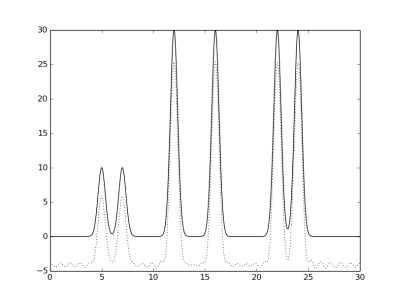
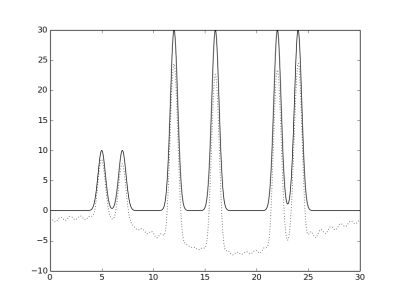
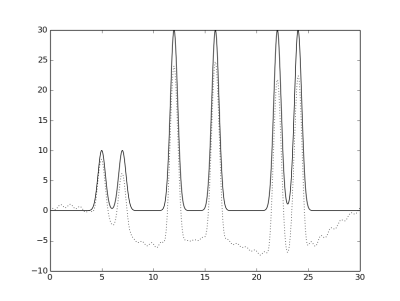
Гармоники 1-30, 2-30, и 3-30, соответственно.
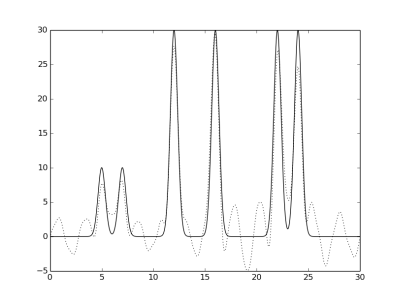

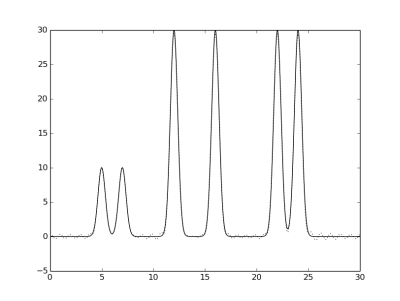
Гармоники 0-10 и 14-30, 0-13 и 17-30, и 0-30 и 40, соответственно.
Так как нулевая гаромника - константна, при отсутствии одной гармоники график сдвигается вниз.
При отсутствии трех гармоник из середины высокие пики все еще различимы, а низкие и пики, возникшие
из-за ошибок приближения различаются уже с трудом.
Если же добавить гармонику высокого номера (использовалась 40-я), никаких существенных улучшений
замечено не было, что и согласуется с нашими ожиданиями.
Ниже приведена таблица с информацией по проделанной работе:
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум амплитуды (% от величины F) | Шум фазы (% от величины Phase) | Качество восстановления |
| Полный набор гармоник | |||||
| 0-5 | 6 | 100 | 0 | 0 | Плохое |
| 0-10 | 3 | 100 | 0 | 0 | Плохое |
| 0-15 | 2 | 100 | 0 | 0 | Среднее |
| 0-20 | 1.5 | 100 | 0 | 0 | Среднее |
| 0-25 | 1.2 | 100 | 0 | 0 | Хоршее |
| 0-30 | 1 | 100 | 0 | 0 | Отличное |
| 0-30 | 1 | 100 | 20 | 0 | Хорошее |
| 0-30 | 1 | 100 | 0 | 20 | Среднее |
| 0-30 | 1 | 100 | 20 | 20 | Плохое |
| 0-30 | 1 | 100 | 15 | 15 | Отличное |
| 0-30 | 1 | 100 | 10 | 10 | Отличное |
| Неполный набор гармоник | |||||
| 1-30 | 1.03 | 97 | 0 | 0 | Отличное |
| 2-30 | 1.07 | 93 | 0 | 0 | Хорошее |
| 3-30 | 1.11 | 90 | 0 | 0 | Хорошее |
| 0-10 и 14-30 | 1.11 | 90 | 0 | 0 | Среднее |
| 0-13 и 17-30 | 1.11 | 90 | 0 | 0 | Среднее |
| 0-30 и 40 | 1 | 100 | 0 | 0 | Отличное |