Реконструкция электронной плотности по данным РСА: одномерная модель

Создание функции ЭП в одномерной элементарной ячейке

Для начала необходимо было создать модель 5-7 атомов.

С помощью скрипта compile-func.py построили одномерную функцию электронной плотности модели шести атомов:

compile-func.py -g 30,2,7+18,3,8.5+18,2,9.5+2,3.5,21+18,2,22+30,3,23.5 -o goodfunc1.txt

График электронной плотности показан на рисунке 1. Низкий четвертый пик изображает атом водорода.

Рис. 1. График одномерной электронной плотности. Координаты точек в файле

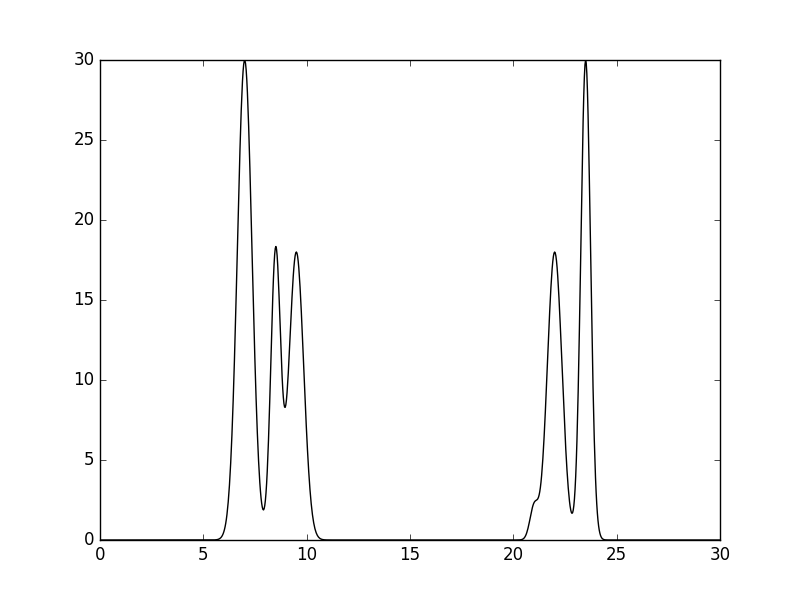
Расчет коэффициентов Фурье

Для полученной функции ЭП рассчитали коэффициенты Фурье для 500 гармоник с помощью скрипта func2fourier.py. Скрипт выдает файл с амплитудой и фазой для каждой гармоники.

Восстановление функции ЭП

Из файла с амплитудами и фазами восстанавливали функцию ЭП с помощью скрипта fourier2func.py. Это проделали несколько раз с разным количеством гармоник. На рисунке 2 изображен график восстановленой по всем 500 гармоникам ЭП. Восстановление идеальное, то есть исходная и восстановленная функция полностью совпали.

Рис. 2. ЭП, восстановленная по 500 наборам коэффициентов Фурье

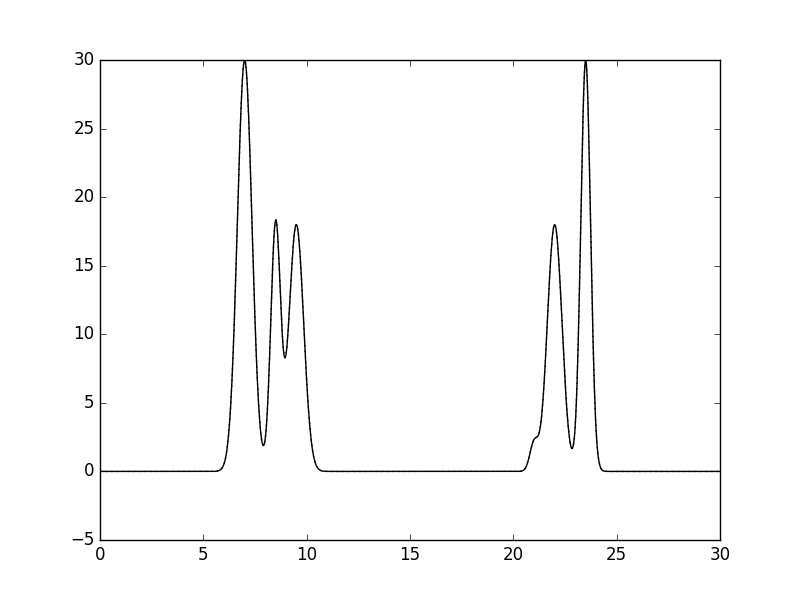
Критерии для качества восстановления ЭП следующие:
Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".

1. Полный набор гармоник

Необходимо найти минимальный набор гармоник, при котором восстановление отличное. Последовательно увеличивали количество гармоник для восстановления (см. рисунок 3). При гармониках 0-21 не разделяются второй и третий пики, остальные высокие пики хорошо видны. В следующем восстановлении 0-32 они четко разделяются. Однако низкий четвертый пик (водорода) не отличим от пиков шума в правой части графика. При числе гармоник, равном 36, пики всех шести атомов угадываются по восстановленной функции.

Рис. 3. Поиск числа гармоник, при котором набор гармоник полный (восстановления от плохого до отличного). Цифрами обозначены выбранные гармоники из списка 500 гармоник. Пунктиром обозначена восстановленная функция.

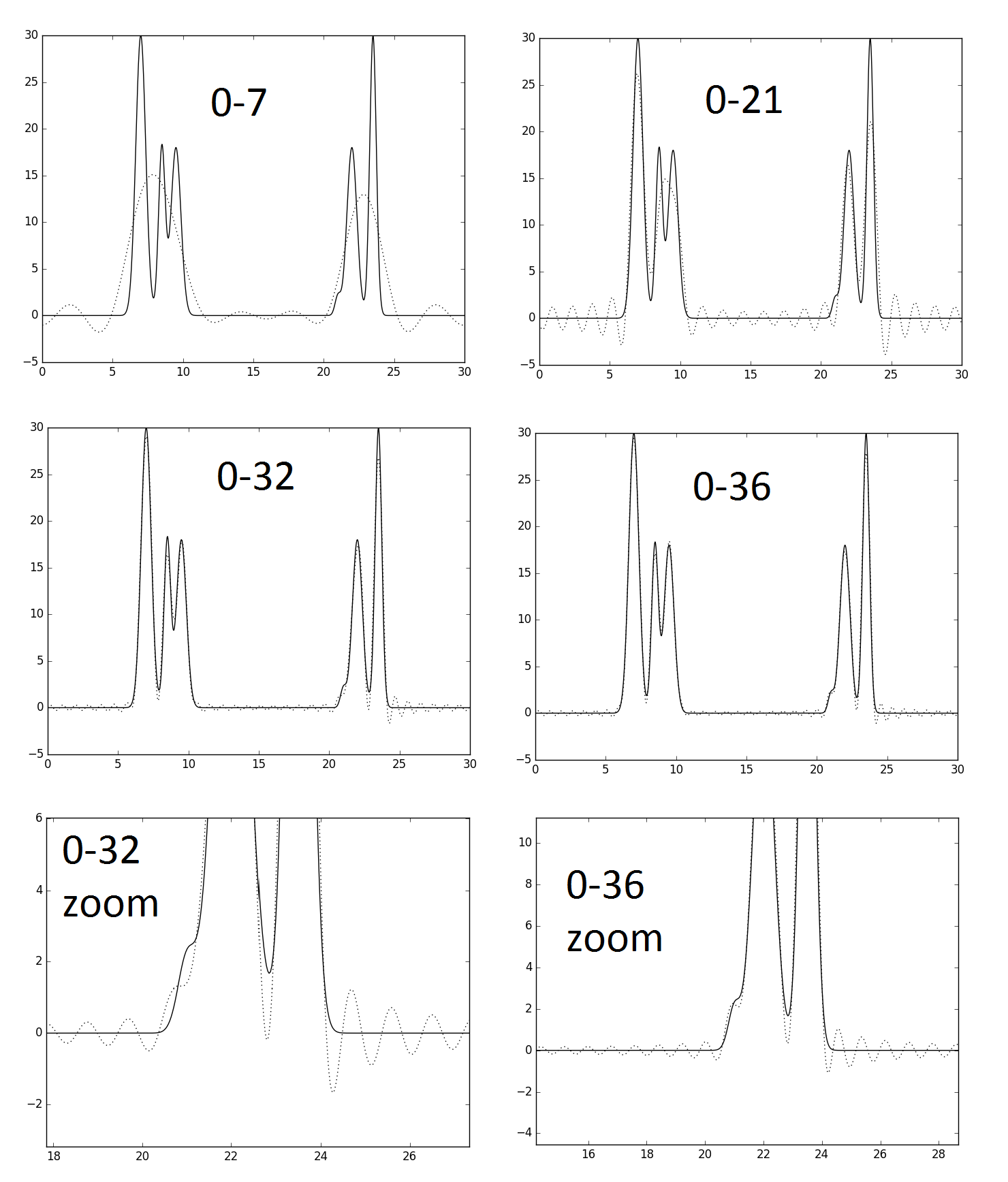
При восстановлении по полному набору гармоник (0-36) добавили шум к коэффициентам Фурье. Сначала добавляли шум к амплитудам и к фазам, затем к обоим коэффициентам (рис. 4). Можно сказать, что шум в фазах вносит большую погрешность, чем шум в амлитудах. При P=60 ни один пик атомов модели не отличим от шумовых пиков, а при F=60 видно три максимума.

Рис. 4. Восстановление по полному набору 0-36 с шумом амплитуд гармоник (F=30;60), фаз (P=30;60); амплитуд и фаз.

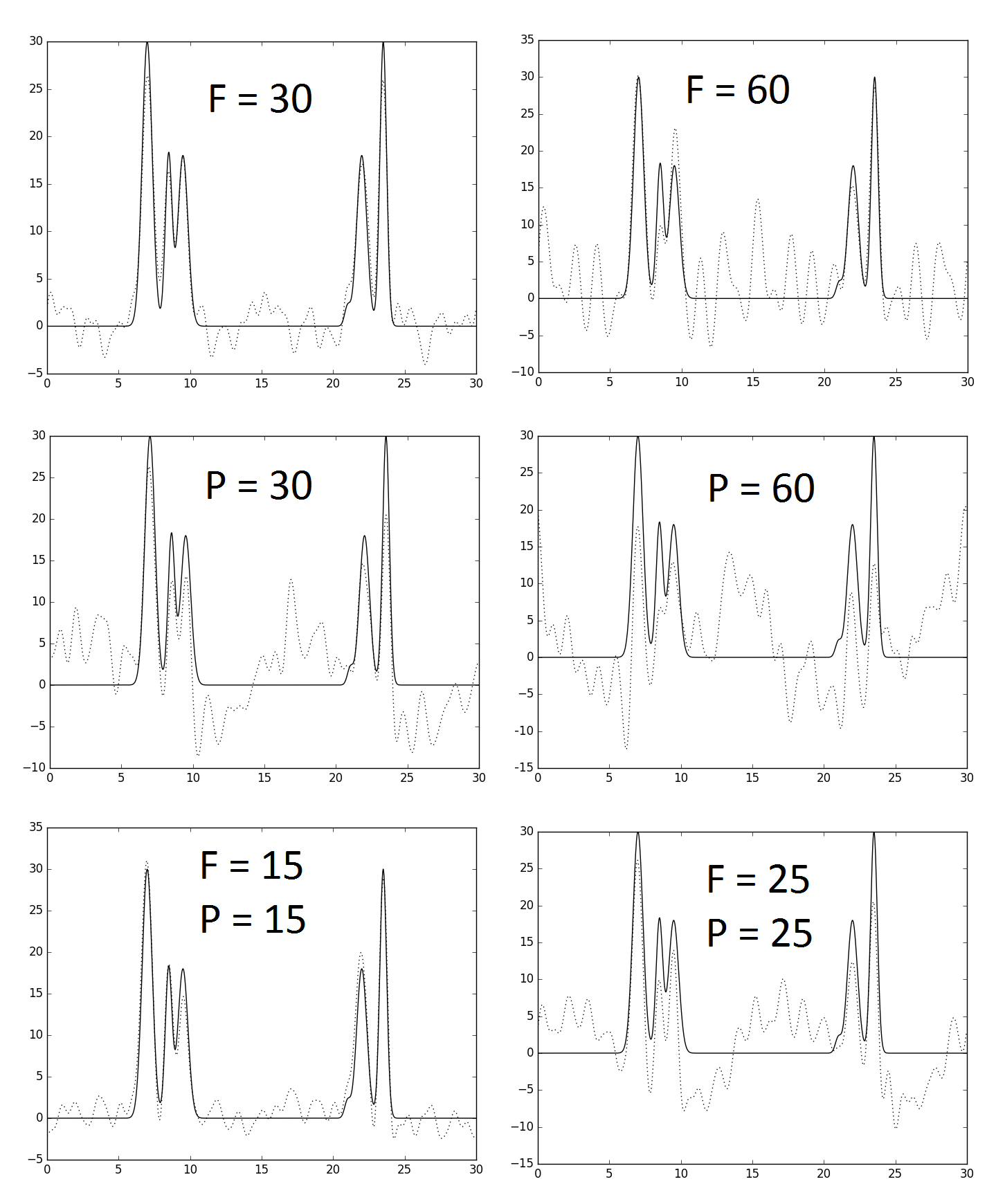
2. Неполный набор гармоник

Набор гармоник ряда Фурье окажется неполным, если убрать несколько гармоник из 0-36 (полного набора). При удалении первой гармоники график сдвинулся вниз на константу, ведь первая гармоника не имеет фазы, это не волновая функция (рис. 5). Восстановление оказалось отличным, как и в случае удаления первых двух гармоник.

Рис. 5. Восстановление по неполному набору гармоник: удаление первых гармоник.

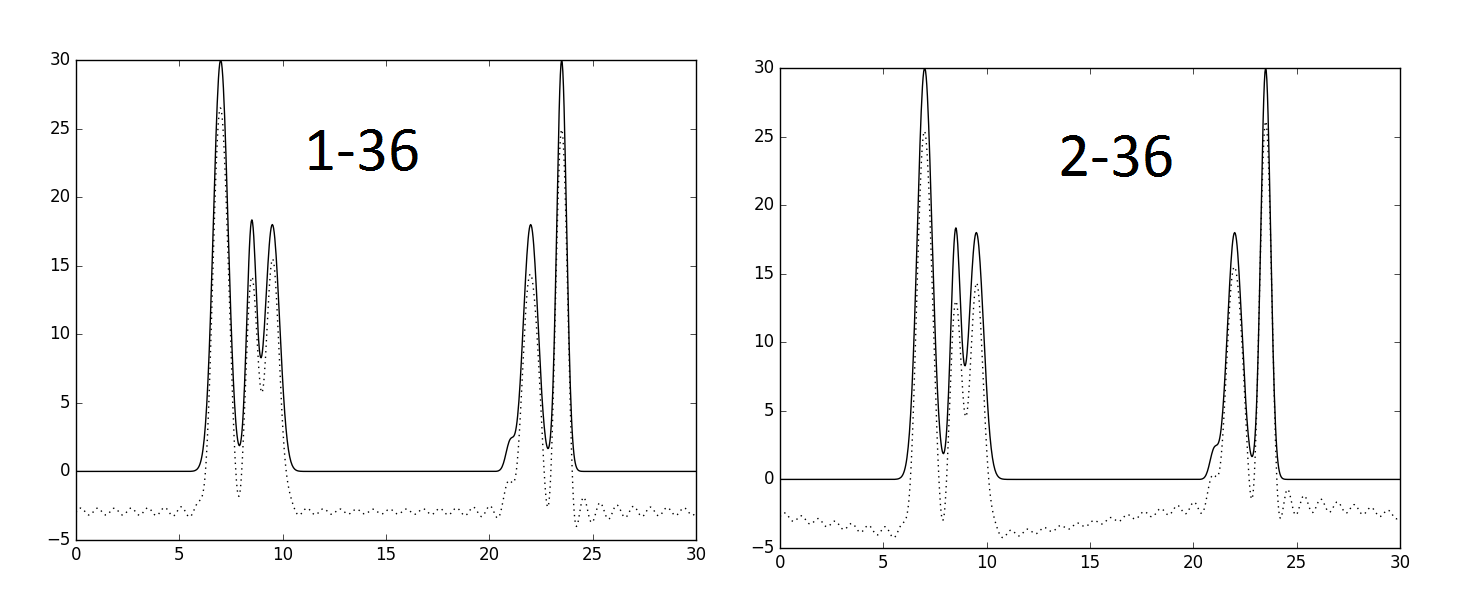
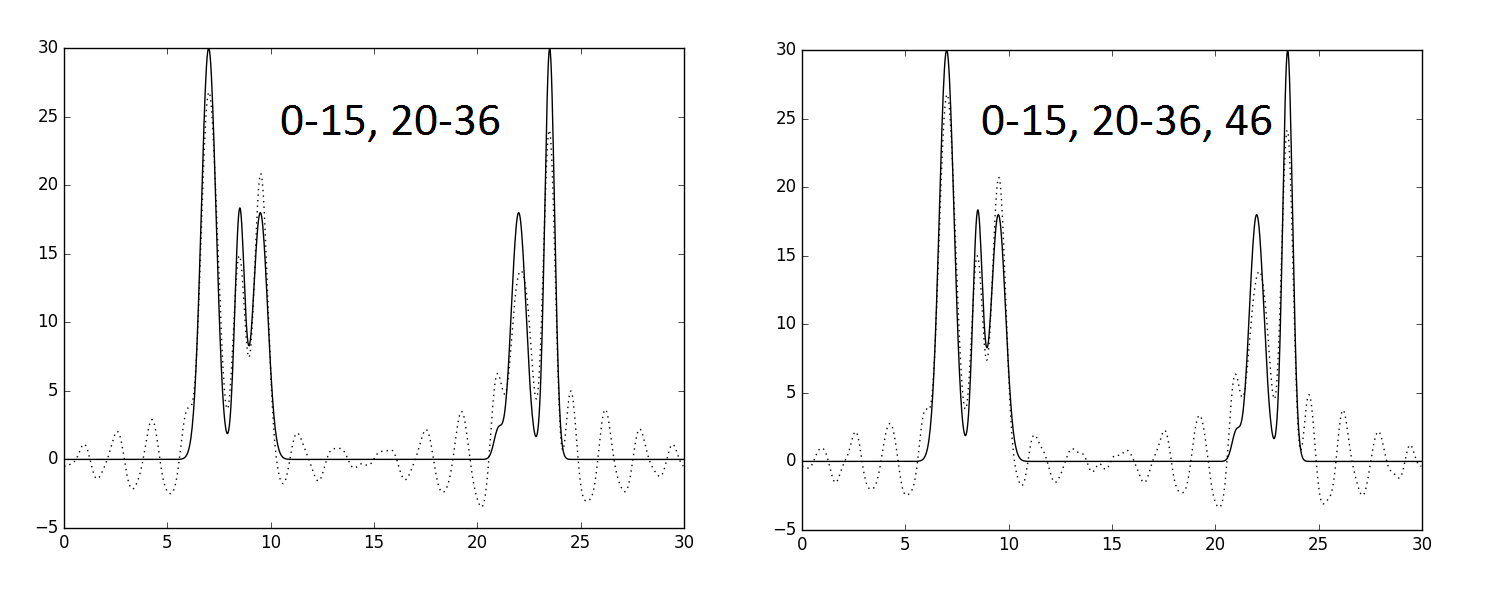
Но при удалении четырех гармоник из середины набора восстановление функции ухудшилось. Не все пики атомов удается отличить от шума. Если добавить к такому восстановлению еще одну гармонику под номером 46, то график фактически никак не изменится. Видимо, дело в том, что, чем больше номер гармоники в наборе, тем меньше ее период. То есть 46 гармоника выполняет роль "тонкой настройки" формы графика. Поэтому при отсутствии серединных гармоник, которые "грубо" задают форму графика, добавление 46 гармоники не улучшает восстановление.

Рис. 6. Восстановление по неполному набору гармоник: удаление 10% гармоник из середины набора; добавление 46 гармоники к полученному набору.

3. Разрешение набора гармоник

Если мы имеем все гармоники 0...n, то такой набор гармоник – полный. Его разрешение равно меньшему периоду из всех периодов гармоник, то есть периоду гармоники n. Он высчитывается как d=T/n, где T=30Å в нашем случае, а n-номер самой высокочастотной известной гармоники.

Если нам не известно какое-то количество гармоник из набора 0...n, то это неполный набор, и для него нет единого правила расчета разрешения. Можно выбрать самую высокочастотную гармонику из известных (назовем ее номер n*) и высчитать ее разрешение как d*=T/n*. Каждому такому разрешению набора соответствует полнота данных. Полнота – процент известных гармоник с разрешением большим или равным d* среди всех гармоник с разрешением большим или равным d*. Если полнота данных слишком мала, нужно выбрать другую гармонику n* с большим разрешением. Мы выберем порог полноты данных 90%.

Например, рассчитаем разрешение для неполного набора гармоник 0-15,20-36,46 (рис. 6, справа):
30/46 = 0.7 Å с полнотой 33/46*100% = 72%
30/36 = 0.8 Å с полнотой 32/36*100% = 89%

89% округлим до 90%, поскольку небольшое увеличение разрешения в этом случае не вызывает рост полноты. Разрешение такой структуры равно 0.8 Å при полноте данных 90%.

Результаты всех восстановлений функции ЭП занесены в таблицу 1.

Таблица 1. Восстановление функции ЭП по коэффициентам Фурье.

← Назад к семестру