Страница седьмого семестра

Задание функции

На отрезке [0,30] Å расположены две молекулы: 3 атома + 2 атома. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. Молекулы расположены на расстоянии 4-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.
Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py:

C:/Python27/python compile-func.py -g 34.3,2.9,3+30.2,3,4.2+24.2,3,5.5+13.8,3.2,10+4.3,3,11.2

В результате получаем выходной файл скрипта с парами (Х,У) и график функции: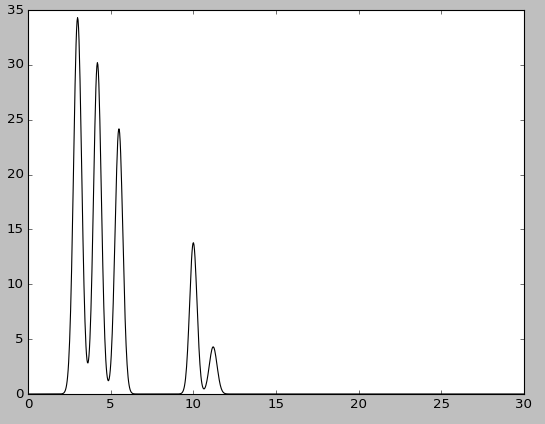

Рис. 1. График электронной плотности молекулы

Коэффициенты Фурье для полученной функции рассчитываются с помомщью скрипта func2fourier.py:

C:/Python27/python func2fourier.py -i func.txt -o coef_fourier.txt

В файле coef_fourier.txt содержатся информация об амплитудах и фазах всех гармоник из разложения функции в ряд Фурье с их порядковыми номерами.

Полные наборы гармоник

Сравнение восстановленной функции с исходной

При определении n0 тестировались несколько значений: 20, 25, 30, 35. Результат представлен ниже.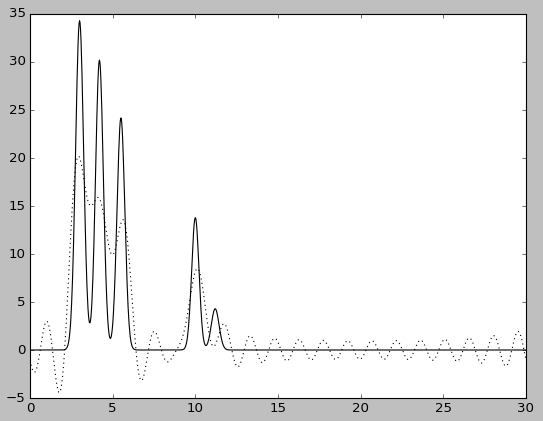


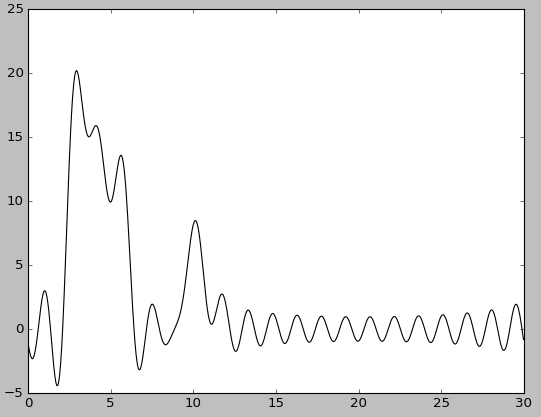n0=20	n0=20, без исходной функции

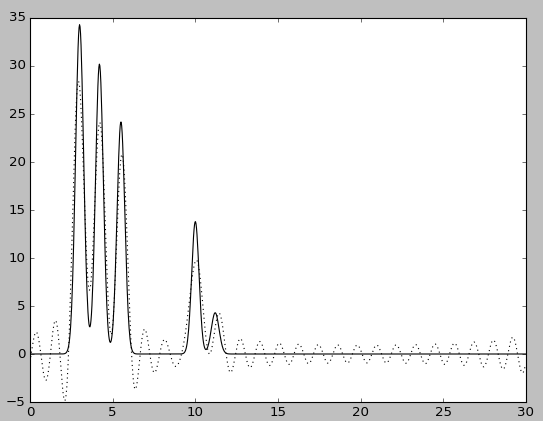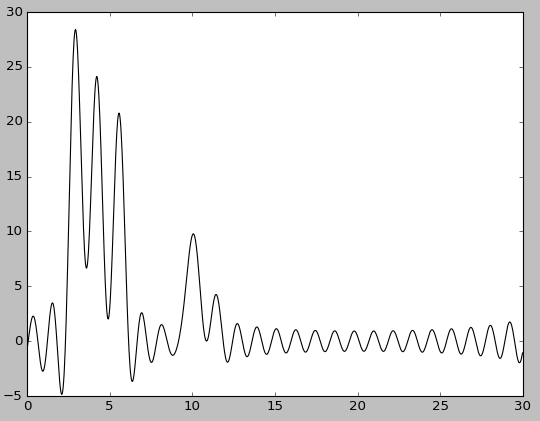n0=25	n0=25, без исходной функции

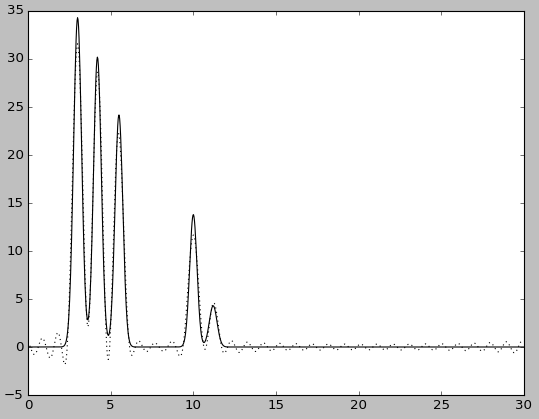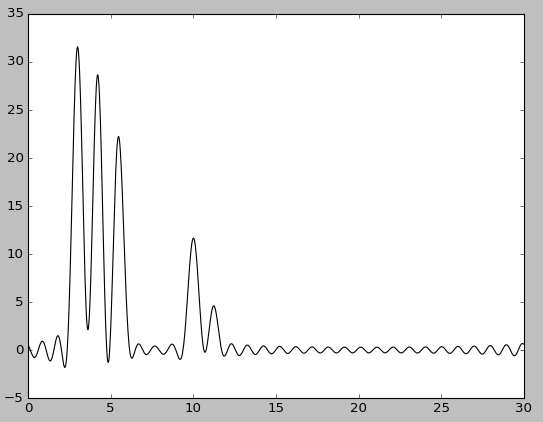n0=30	n0=30, без исходной функции

При полном наборе 30 гармоник восстановление отличное - по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов") , следовательно, n0 = 30.

При полном наборе 25 гармоник востановление хорошее - то есть можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы атомов не отличимы от шума.

При полном наборе 20 гармоник востановление среднее - положение каких-то атомов определить по восстановленной функции нельзя, других - можно

Добавление шума

На амплитуды и фазы гармоник из полного набора n0 был наложен шум разной величины с помощью скрипта func2fourier.py.

C:/Python27/python func2fourier.py -i func.txt -o coef_fourier_FPnoise_5.txt -P 5 -F 5

Результаты представлены ниже.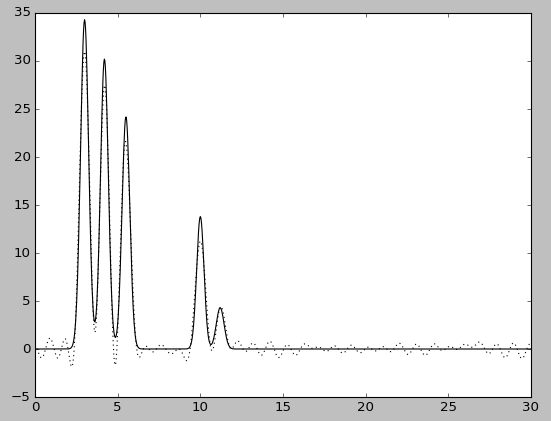


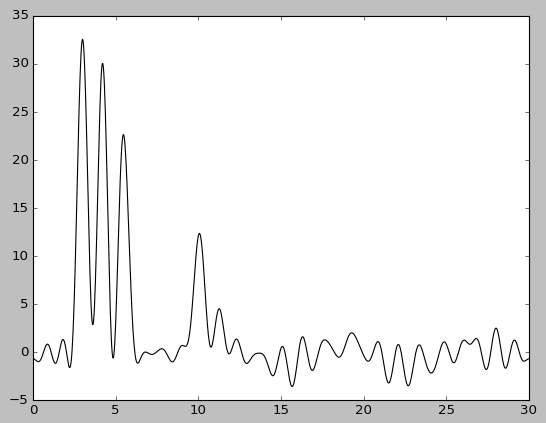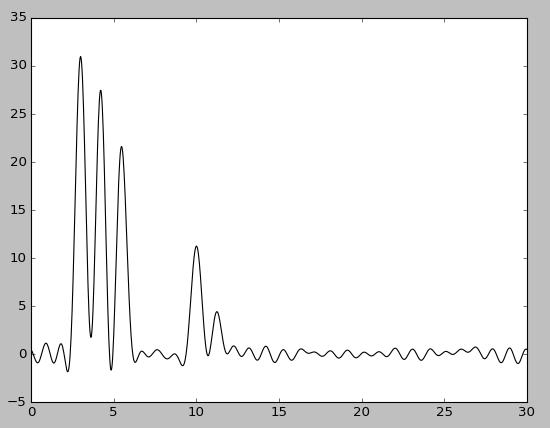
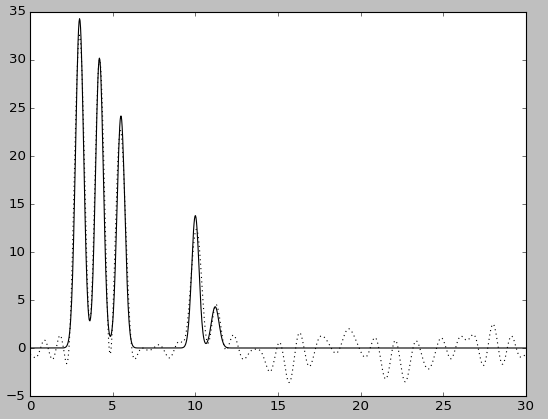
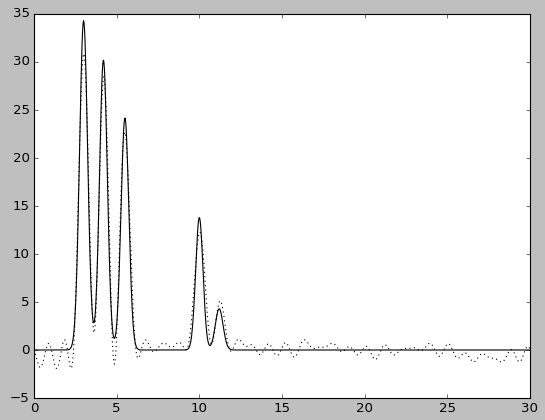
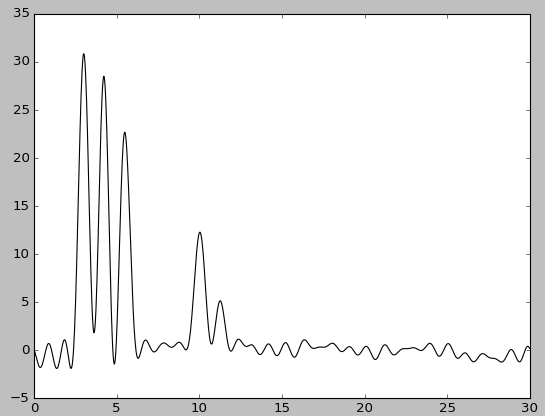
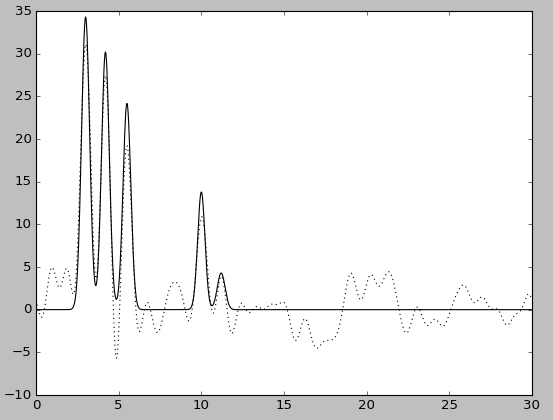
F=5	F=5, без исходной функции	F=20	F=20, без исходной функции

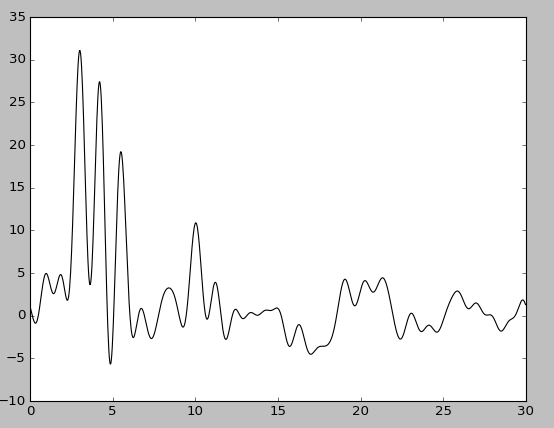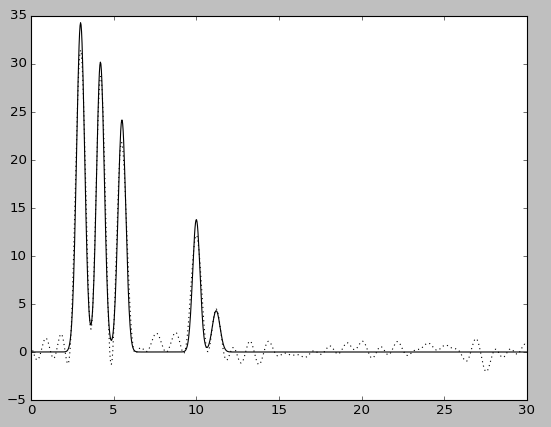
P=5	P=5, без исходной функции	P=20	P=20, без исходной функции

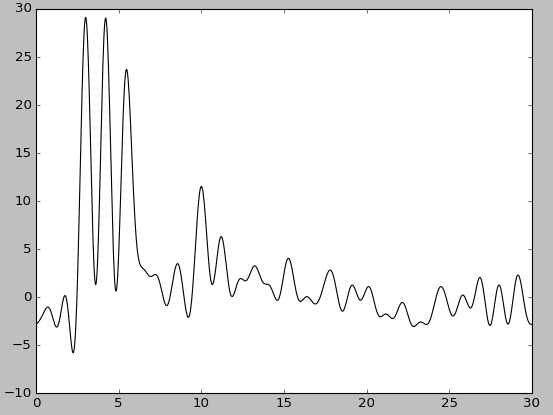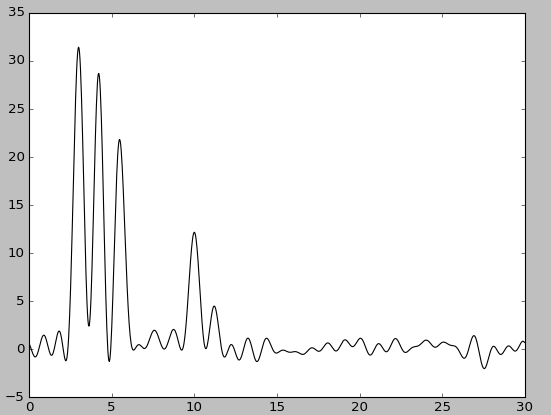
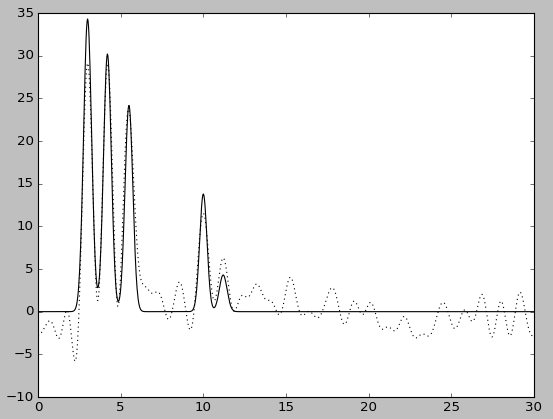
F = 5, P=5	F = 5, P=5, без исходной функции	F = 10, P=10	F = 10, P=10, без исходной функции

При этом качество восстановления снизилось: при добавлении 20% шума к амплитуде - до хорошего, при добавлениии шума такого же размера к фазе - до среднего. Попеременное добавление 5% шума к амплитуде или к фазе практически ничего не меняет, в то время как одновременное добавление 5% шума снижает качество восстановления до хорошего, а 10% - до среднего.

Неполные наборы гармоник

Удаление начальных гармоник

Для получения неполного набора гармоник были удалены первая или первые 2 гармоники.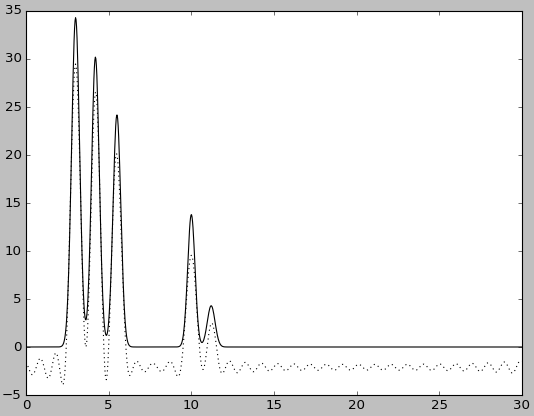


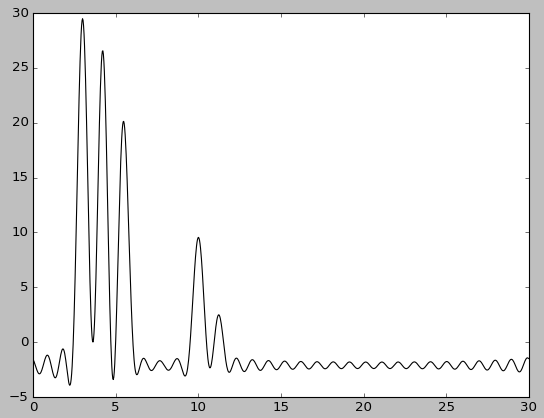Гармоники 1-30	Гармоники 1-30, без исходной функции

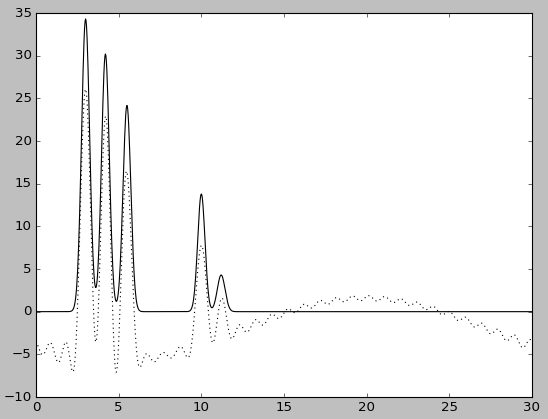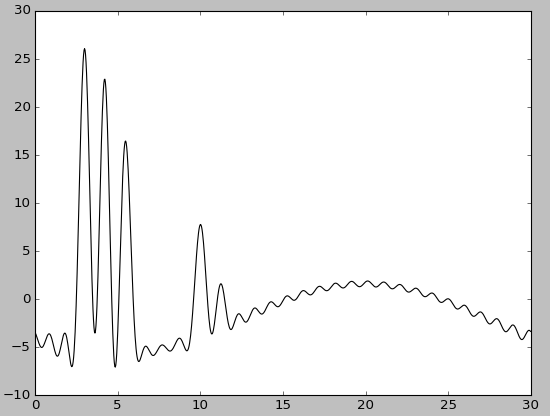Гармоники 2-30	Гармоники 2-30, без исходной функции

При удалении небольшого количества начальных гармоник качество восстановления не изменяется: несмотря на сильное смещение уровня графика (в случае удаления первой гармоники) или измение базовой линии (в случае удаления первых двух гармоник), положение максимумов определяется однозначно.

Удаление гармоник из середины набора

Были удалены 6.67% гармоник полного набора (2, 21-22). При этом качество восстановления резко упало до среднего.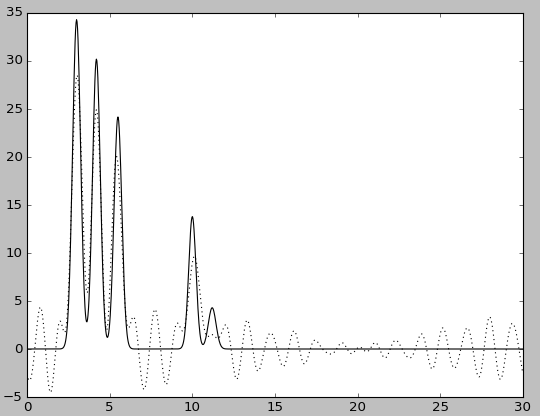


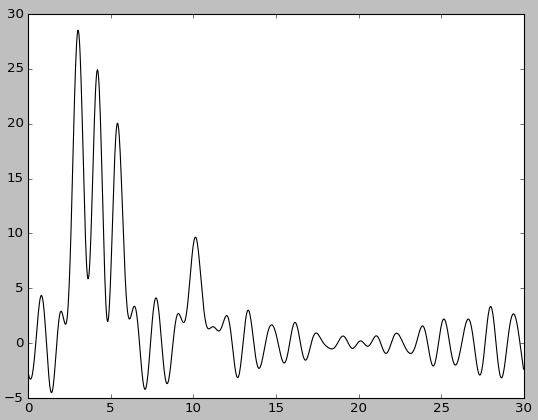Гармоники 1-20, 23-30	Гармоники 1-20, 23-30, без исходной функции

Добавление гармоники n0+10

К полному набору гармоник (30) добавили еще одну, 40. При том график принципиально не изменился, качество восстановления отличное.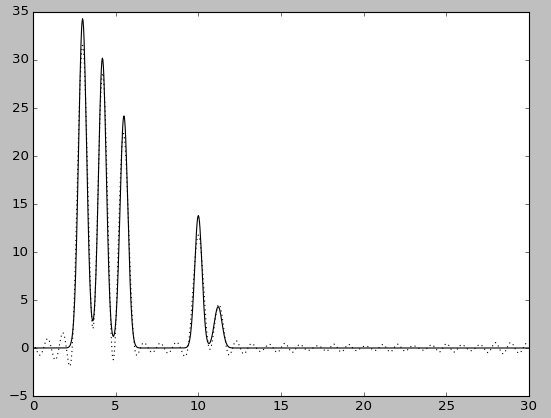


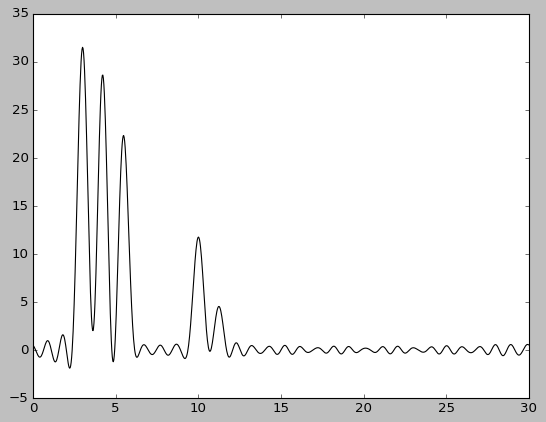Гармоники 1-30, 40	Гармоники 1-30, 40, без исходной функции

Определение разрешения и полноты данных

Разрешением полного набора гармоник называется период гармоники с номером n, т.е. с наибольшим номером. Зависимость длины волны от номера гармоники:

0 – гармоника есть константа, длины волны нет
1 – длина волны равна длине отрезка T ; в наших заданиях T = 30 Å
2 – — " — T/2 (15 Å в заданиях)
3 – — " — T/3 (10 Å в заданиях)
...............
n – — " — T/n (30/n Å в заданиях)

Таким образом, разрешение для n0 = 30 равно 30 Å / 30 = 1 Å. Для непоных наборов гармоник разумно также указывать полноту данных - процент гармоник с длиной волны БОЛЬШЕЙ d от максимально возможного, присутствующих в наборе.

Набор гармоник	Разрешение, Å	Полнота данных, %	Шум амплитуды (% от F)	Шум фазы (% от phi)	Качество восстановления
Полный набор гармоник
0-20	1.5	100	0	0	Среднее
0-25	1.2	100	0	0	Хорошее
0-30	1	100	0	0	Отличное
0-30	1	100	5	0	Отличное
0-30	1	100	0	5	Отличное
0-30	1	100	20	0	Хорошее
0-30	1	100	0	20	Среднее
0-30	1	100	5	5	Хорошее
0-30	1	100	10	10	Среднее
Неполный набор гармоник
1-30	1	96.8	0	0	Отличное
2-30	1	93.5	0	0	Отличное
0-20, 23-30	1	93.5	0	0	Среднее
0-30, 40	1	100	0	0	Отличное

Построение и визуализация электронной плотности