Множественное выравнивание последовательностей белков

Сравните выравнивания одних и тех же последовательностей разными программами

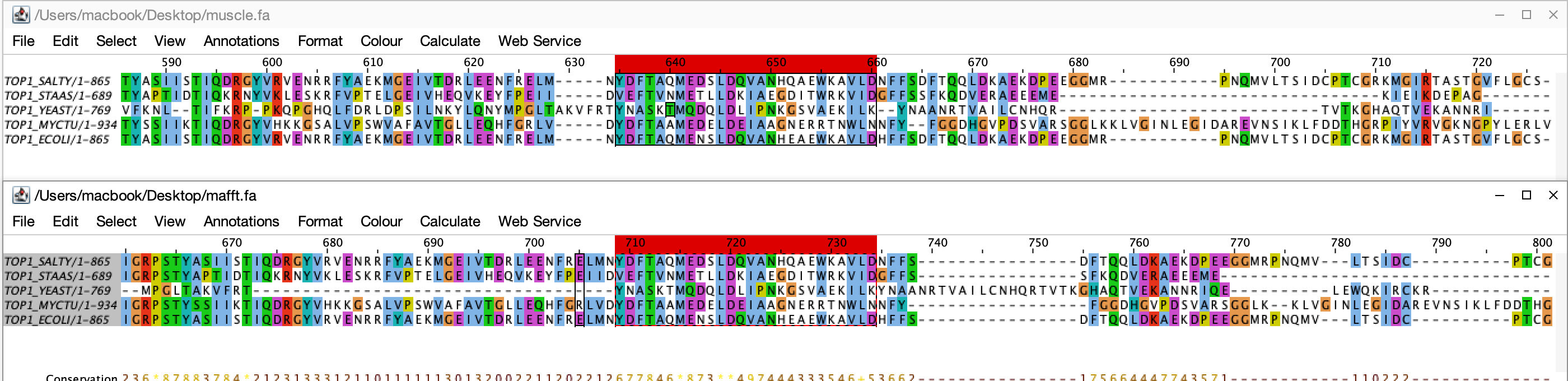
Я использовала белки семейства TOP1 - DNA topoisomerase 1, которые использовала в практикуме 9. Я выбрала 5 белков, 3 из которых имеют известную вторичную структуру в PDB (для задания 3). В Jalview я построила 2 выравнивания: Muscle и Mafft для 5 белков из семейства TOP1: TOP1_ECOLI, TOP1_STAAS, TOP1_YEAST, TOP1_MYCTU, TOP1_SALTY.

Ссылка на проект Jalview с двумя выравниваниями

Для сравнения выравниваний я использовала программу Егора, Яши, Артема и Матвея (просто потому, что ее проще скачать и по интерфейсу она приятнее. молодцы!!). В выходном файле получила только один совпадающий блок: 635-660 в выравнивании MUSCLE и 709-734 в выравнивании MAFFT. Последовательности большие, а вот совпадающих столбцов мало. Почему?
Последовательности длинные (min=689 АК), поэтому даже по судя по размеру количество выравниваний большое и вероятность отличий двух программ высока
Последовательности обладают разными длинами, причем есть сильно выбивающиеся из остальных: TOP1_STAAS - 689 АК, TOP1_YEST - 769 AK, TOP1_SALTY & TOP1_ECOLI - 865 AK,и TOP1_MYCTU - 934 AK. Такая разная длина говорит о том, что в выравниваниях будет большое количество гэпов

Я думаю, что у этих выравниваний совпадают гомологичные блоки белков, а вариативные - нет.

Построение выравнивания по совмещению структур и сравнение его с выравниванием MSA

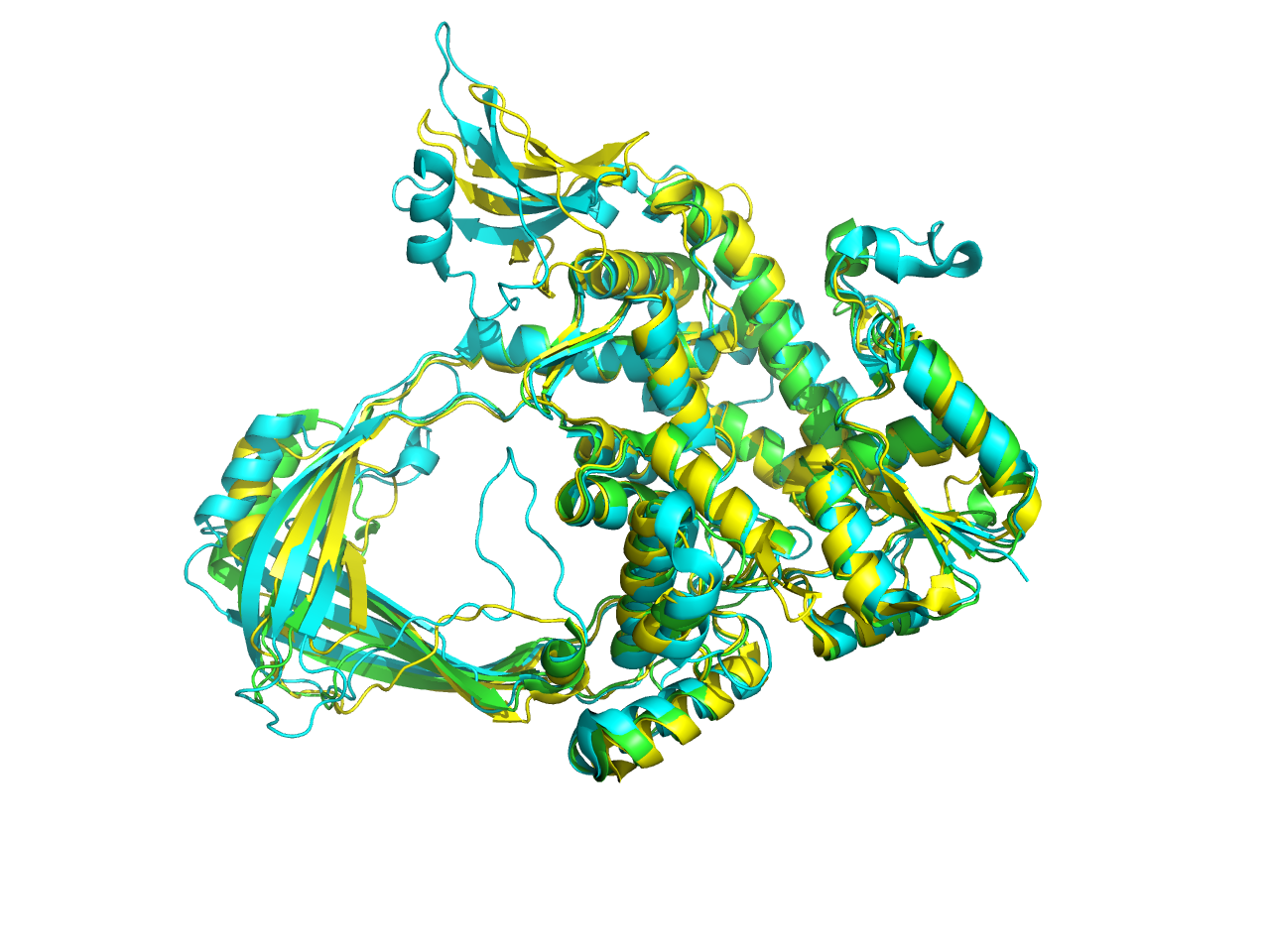
Я выбрала белки TOP1_THEMA, TOP1_MYCTO, TOP1_ECOLI. Загрузила их структуры в PyMOL и применила 'alignment'. Белки очень хорошо выровнены, что показано на Рис. 2. Вторичная структура у них одинаковая, кроме петель (понятно, почему они по-разному выглядят) и концевых участков (и с С-, и с N- конца), где отсутствуют АК у одного из белков.

Проверим это выравнивание в JalView, например с помощью Muscle.

Тут ссылка на выравнивание. По нему видно, что выравнивание Muscle соответствует выравниванию в PyMOL, потому что мы видим крупные совпадающие блоки в начале и середине последовательностей, а в конце хорошо выровнены 2 последовательности (так как 3-я короче и не участвует на N-конце в выравнивании).

Описание работы программы Muscle

Muscle - MUltiple Sequence Comparison by Log-Expectation (Множественное выравнивание последовательностей с помощью логарифмического ожидания). При этом Muscle может использоваться для выравнивания белков и нуклеиновых кислот. Впервые была опубликована Робертом С. Эдгаром в 2004 году в журналах BMC Bioinformatics и Nucleic Acids Research.

Описание алгоритма

Этап 1, Прогрессивный этап. Цель первого этапа — произвести множественное выравнивание, делая упор на скорость, а не на точность.
1. Создание матрицы расстояний, элементами которой являются расстояние k-меров ждя каждой пары последовательностей.
2. На основе матрицы создается бинарное дерево
3. Построение прогрессивного выравнивания в соответствии с порядком ветвления дерева с помощью алгоритма Нидлмана-Вунша: на каждом внутреннем узле строится парное выравнивание двух дочерних профилей, создавая новый профиль, который и назначается этому узлу. То есть происходит многократное выравнивание всех последовательностей.

Этап 2, Улучшенный прогрессивный этап. Повторная оценка дерева с помощью расстояния Кимуры, которое является более точным, чем приблизительная мера расстояний k-меров, но требует выравнивания.
1. Создание матрицы расстояний, элементами которой являются расстояния Кимуры (1983) для каждой пары последовательности
2. На основе матрицы создается бинарное дерево
3. Построение прогрессивного выравнивания (аналогично предыдущему, с помощью алгоритма Нидлмана-Вунша), создается множественное выравнивание. Порядок ветвления поддеревьев в двух этапах разное.

Этап 3, Уточнение.
1. Выбор ребра из дерева этапа 2 (ребро выбирается в порядке приближения к корню)
2. Вычисление профиля множественного выравнивания каждого поддерева, которые получились путем удаления ребра из дерева.
3. Новое множественное выравнивание строится путем выравнивания двух профилей.
4. Если оценка SP (sum of pair) улучшается, то выравнивание сохраняется, а если нет, то сбрасывается.
Шаги 1-4 повторяются, пока не будет достигнута сходимость или заданный пользователем предел.

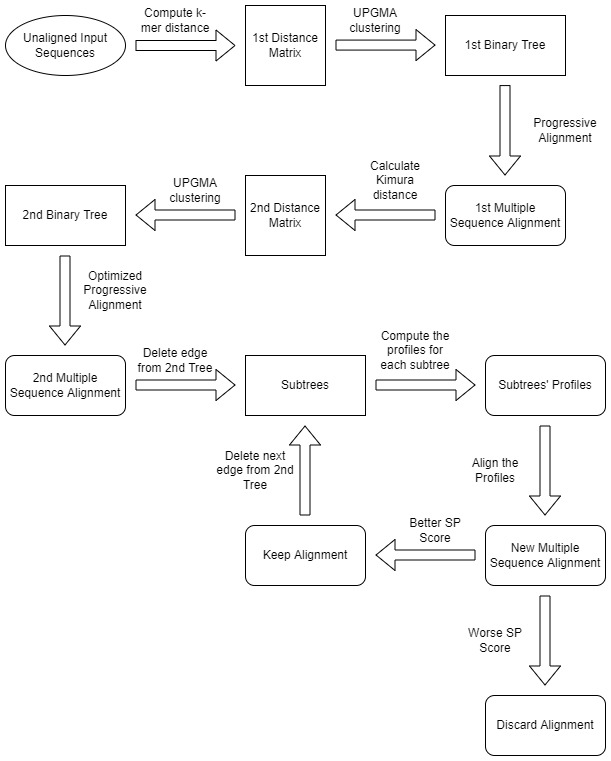
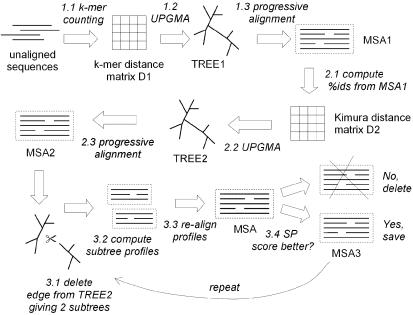
Рис. 3. Схемы работы алгоритма Muscle, представленные в работах С.Эдгара^[1] и более новая версия.

Литература

[1] Edgar RC (2004). "MUSCLE: a multiple sequence alignment method with reduced time and space complexity". BMC Bioinformatics. 5 (1): 113. doi:10.1186/1471-2105-5-113. PMC 517706. PMID 15318951
[2] Edgar RC (2004). "MUSCLE: multiple sequence alignment with high accuracy and high throughput". Nucleic Acids Research. doi:10.1093/nar/gkh340. PMC 390337. PMID 15034147