export PATH=$PATH:/home/preps/grishin/open3dtools/bin
Для начала необходимо построить пространственное выравнивание активных конформаций исследуемых веществ. Будем считать активной конформацией (то есть конформацией, в которой вещество-ингибитор взаимодействует с белком-мишенью) наиболее энергетически выгодную конформацию. Сгенерируем эти конформации, используя программу obconformer из пакета OpenBabel: obconformer 100 100 compounds.sdf > compounds_best_conformer.sdf
Cделаем выравнивание полученных конформеров с помощью программы Open3DALIGN. Запуск программы:
open3dalign.sh
import type=SDF file=compounds_best_conformer.sdf
align object_list=1
save file=aligned.sdf
Т.к. программа Open3DALIGN сохраняет SDF файл c выравненными веществами в кодировке нашей локали,она, например, юникод, PyMOL такие файлы может отказаться читать. Перекодировать из юникода в ascii:
iconv -c -f utf-8 -t ascii aligned.sdf > aligned_ascii.sdf
Удалить ненужную информацию из заголовков и добавить $$$$ в конец каждой записи:
sed -e 's/.*HEADER.*\([0-9][0-9]\).*/\1/' -e 's/\(.*M END.*\)/\1\n$$$$/' aligned_ascii.sdf > temp
sed -n '/^[0-9a-zA-Z \$\.-]*$/ p' temp > aligned_ok.sdf
rm temp
Загрузите файл со структурами:
import type=sdf file=aligned_ok.sdf
Загрузите файл с данными об активности исследуемых соединений (activity.txt):
import type=dependent file=activity.txt
Задание решетки вокруг исследуемых соединений:
box
Oставим часть наших соединений в качестве тестового набора, и не будем использовать их для построения модели, а также исключим (пока что) соединения с неизвестной активностью:
set object_list=60-85 attribute=TEST
set object_list=86-88 attribute=EXCLUDED
Рассчитаем значения энергии ван-дер-Ваальсовых взаимодействий в узлах решетки:
calc_field type=VDW force_field=MMFF94 probe_type=CR
В некоторых узлах решетки псевдо-атом зонда (probe) находится слишком близко к атомам исследуемых соeдинений и дает слишком большую по модулю энергию. Установим ограничения на значения энергии:
cutoff type=max level=5.0 field_list=1
cutoff type=min level=-5.0 field_list=1
Слишком маленькие значения энергии приравняем к 0:
zero type=all level=0.05
Исключим из анализа ячейки, в которых вариабельность в энергии взаимодействия с зондом для разных соединений мала:
sdcut level=0.1
nlevel
remove_x_vars type=nlevel
Построим регрессионную модель:
pls
Полученные коэффициенты корреляции для разного количества компонент, выделенных PLS:
Exp. Cum. exp. Exp. Cum. exp.
PC var. X % var. X % var. Y % var. Y % SDEC r2
--------------------------------------------------------------------------
0 0.0000 0.0000 0.0000 0.0000 0.9494 0.0000
1 15.9480 15.9480 32.8386 32.8386 0.7780 0.3284
2 5.1333 21.0813 36.3625 69.2011 0.5269 0.6920
3 4.6235 25.7048 15.6991 84.9002 0.3689 0.8490
4 3.8908 29.5956 7.5246 92.4248 0.2613 0.9242
5 4.0108 33.6064 2.8661 95.2909 0.2060 0.9529
Elapsed time: 0.2967 seconds.
r2 (r^2) для большинства компонент >0 и близок к 1. Поэтому полученную модель можно считать хорошей.Кросс-валидация:
PC SDEP q2 -------------------------- 0 0.9658 -0.0348 1 0.9164 0.0683 2 0.9733 -0.0509 3 0.9667 -0.0368 4 0.9880 -0.0829 5 0.9497 -0.0006 Elapsed time: 1.5029 seconds. END COMMAND #00.0014 - CV tool succeeded.q2 (оно же r^2) не очень хорошее (<0 или близка к нему).
cv type=loo runs=20
Предсказание активности для тестовой выборки:
predict
PC r2(pred) SDEP -------------------------- 0 0.0000 1.0362 1 0.2655 0.8881 2 0.3296 0.8484 3 0.2353 0.9061 4 0.2754 0.8821 5 0.2536 0.8953 Elapsed time: 0.0208 seconds. END COMMAND #00.0015 - PREDICT tool succeeded.r^2 чуть лучше среднего.
open3dalign.sh import type=SDF file=compounds.sdf align object_list=1 save file=aligned_c.sdf iconv -c -f utf-8 -t ascii aligned_c.sdf > aligned_c_ascii.sdf sed -e 's/.*HEADER.*\([0-9][0-9]\).*/\1/' -e 's/\(.*M END.*\)/\1\n$$$$/' aligned_ascii.sdf > temp sed -n '/^[0-9a-zA-Z \$\.-]*$/ p' temp > aligned_c_ok.sdf rm temp open3dqsar.sh import type=sdf file=aligned_c_ok.sdf import type=dependent file=activity.txt box set object_list=60-85 attribute=TEST set object_list=86-88 attribute=EXCLUDED calc_field type=VDW force_field=MMFF94 probe_type=CR cutoff type=max level=5.0 field_list=1 cutoff type=min level=-5.0 field_list=1 zero type=all level=0.05 sdcut level=0.1 nlevel remove_x_vars type=nlevel pls cv type=loo runs=20 predict
Exp. Cum. exp. Exp. Cum. exp.
PC var. X % var. X % var. Y % var. Y % SDEC r2
--------------------------------------------------------------------------
0 0.0000 0.0000 0.0000 0.0000 1.7139 0.0000
1 15.0134 15.0134 30.0279 30.0279 1.4337 0.3003
2 9.8880 24.9014 16.2796 46.3075 1.2559 0.4631
3 7.1471 32.0485 9.1218 55.4294 1.1442 0.5543
4 7.3622 39.4107 4.7591 60.1884 1.0814 0.6019
5 4.8158 44.2265 6.2423 66.4308 0.9930 0.6643
Elapsed time: 0.1641 seconds.
Значения r^2 здесь ниже.
PC SDEP q2 -------------------------- 0 1.7420 -0.0331 1 1.6679 0.0530 2 1.6959 0.0209 3 1.7622 -0.0572 4 1.8490 -0.1638 5 1.9588 -0.3062 Elapsed time: 0.6023 seconds.q^2 немного лучше.
PC r2(pred) SDEP -------------------------- 0 0.0000 1.0253 1 -0.2270 1.1357 2 -0.0213 1.0361 3 0.0973 0.9742 4 0.1156 0.9642 5 0.0336 1.0079 Elapsed time: 0.0067 seconds.
Сначала переделаем модель с использованием всех имеющихся данных, а вещества с неизвестной активностью обозначим как тестовую выборку:
set object_list=60-85 attribute=TRAINING
set object_list=86-88 attribute=TEST
Построим модель и предскажем активность трех веществ:
pls
predict
Exp. Cum. exp. Exp. Cum. exp.
PC var. X % var. X % var. Y % var. Y % SDEC r2
--------------------------------------------------------------------------
0 0.0000 0.0000 0.0000 0.0000 0.9749 0.0000
1 12.7904 12.7904 44.7278 44.7278 0.7248 0.4473
2 14.5198 27.3102 14.4362 59.1641 0.6230 0.5916
3 6.9345 34.2447 11.1895 70.3536 0.5308 0.7035
4 8.4896 42.7343 5.3685 75.7220 0.4804 0.7572
5 4.7666 47.5009 5.6248 81.3468 0.4211 0.8135
Elapsed time: 0.2160 seconds.
PC SDEP q2 -------------------------- 0 0.9865 -0.0240 1 0.8233 0.2868 2 0.7521 0.4049 3 0.7084 0.4720 4 0.6963 0.4899 5 0.7061 0.4754 Elapsed time: 0.8117 seconds.
PC r2(pred) SDEP -------------------------- 0 0.0000 6.6604 1 0.0315 6.5546 2 -0.0072 6.6842 3 0.0301 6.5593 4 -0.0429 6.8018 5 -0.0891 6.9507 Elapsed time: 0.0066 seconds.
External predictions for dependent variable 1 (activity)
--------------------------------------------------------------------------------------------------------------------------------------
N ID Name Actual 1 2 3 4 5 Opt PC n
--------------------------------------------------------------------------------------------------------------------------------------
86 86 01 0.0000 7.1119 7.5466 7.4119 7.6262 7.7234 1
87 87 44 0.0000 6.9428 7.1202 7.0946 7.3278 7.5477 1
88 88 72 0.0000 5.5073 5.2436 5.1697 5.4378 5.4696 3
export type=coefficients pc=5 format=insight file=coefs
Загрузим в PyMOL файл со структурами, а также получившийся в результате экспорта файл coefs_fld-01_y-01.grd. В этом файле находится информация о коэффициентах модели в каждой точки решетки. Такого рода данные можно визуализовать в PyMOL с помощью команды isosurface, которая рисует поверхность, построенную из всех точек, в которых коэффициенты равны заданному значению:
isosurface positive, coefs_fld-01_y-01, 0.00001
для отображения области, соответствующей коэффициентам 0.00001, и
isosurface negative, coefs_fld-01_y-01, -0.00001
соответственно, для -0.00001.
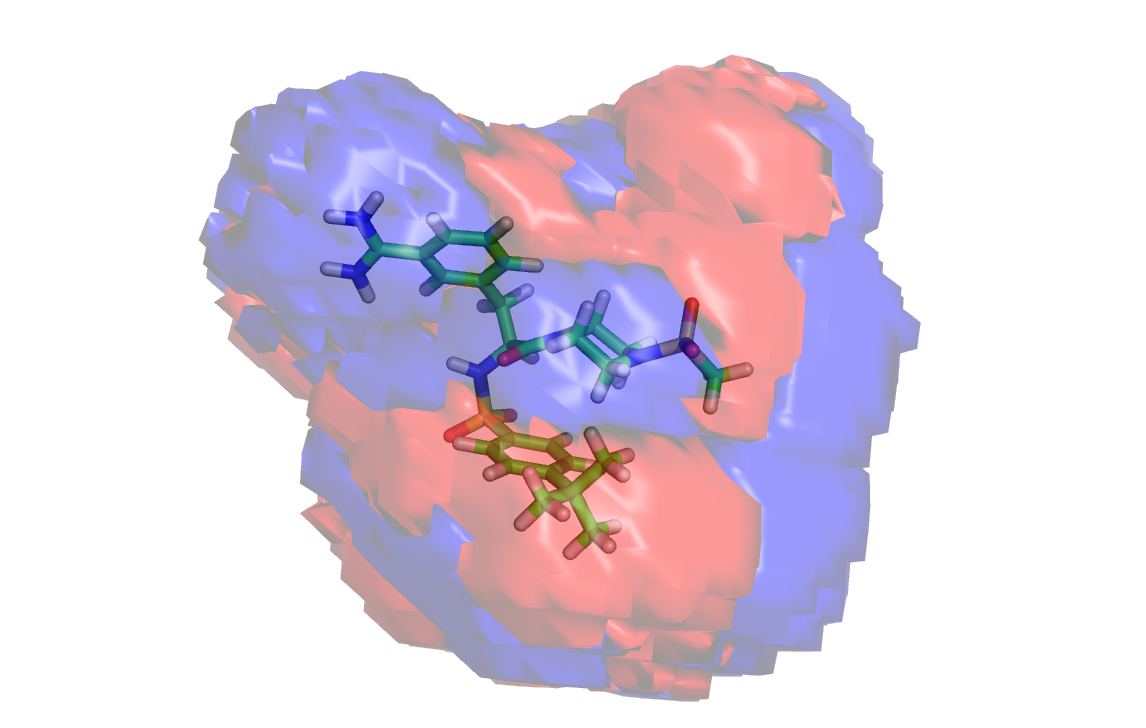
Красным отмечено положительное влияние, синий - отрицательное. Взаимодействие с группами ингибиторов, содержащими серу с остальной молекулой положительно влияют на значение активности, остальные взаимодействия - отрицательно.