Восстановление электронной плотности (ЭП)

Восстановление ЭП

На отрезке [0,30] Å расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 Å друг от друга. Молекулы расположены на расстоянии 3-5 Å (водородная связь или гидрофобное взаимодействие между ними). Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.

Функция была задана с помощью скрипта compile-func.py. На выходе получаем результат работы скрипта с набором пар Х,Y и график электронной плотности (ЭП) молекулы (Рис.1).

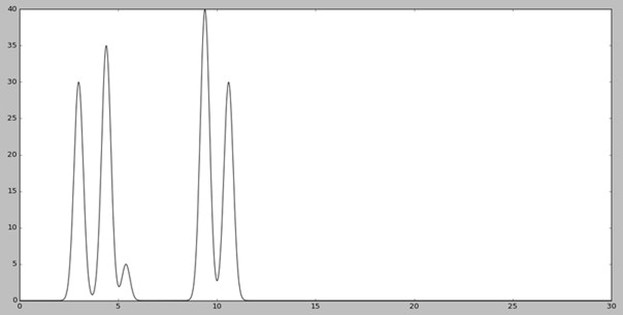
Рис. 1.График функции электронной плотности (ЭП) модели

Для расчета коэффициентов Фурье был использован скрипт func2fourier.py. На входе он получал файл func.txt, полученный скриптом compile-func.py, а на выходе давал файл fourier1.txt (ссылка на файл) с порядковыми номерами амплитуд, а также их фазами и амплитудами, моделирующие экспериментальные данные.

Полный набор гармоник

Восстановление функции ЭП по полному набору гармоник (всего 498 гармоник) выполняется скриптом fourier2func.py. График этой функции (Рис.2) полностью идентичен графику исходной функции (Рис.1).

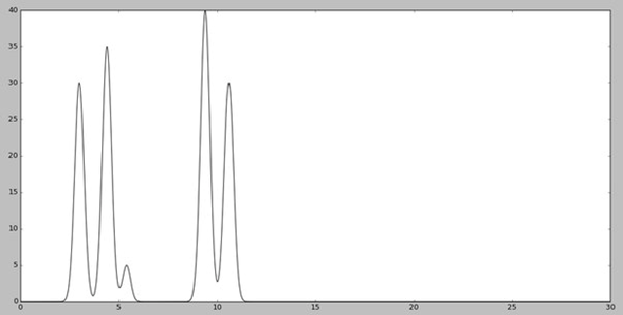
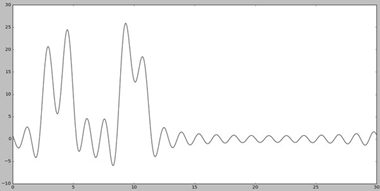
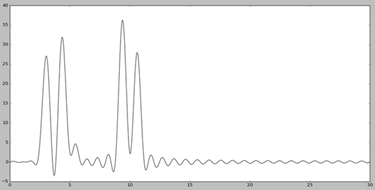
Рис. 2.График функции ЭП, восстановленной по полному набору гармоник

Далее использовался скрипт fourier-filter.py, с помощью которого находится n₀ (число гармоник, при котором восстановление будет отличным). Тестировались значения 20, 25 и 30


n₀ = 20 (без исходной функции)	n₀ = 20

n₀ = 25 (без исходной функции)	n₀ = 25

n₀ = 30 (без исходной функции)	n₀ = 30

Рис. 3.Графики функций, восстановленных по разным n₀ (сплошная) и их наложение на исходную функцию (пунктир)

!На всех следующих рисунках сплошная линия и пунктирная обозначают то же, что на Рис.3!

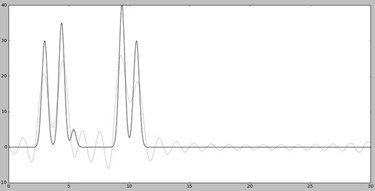
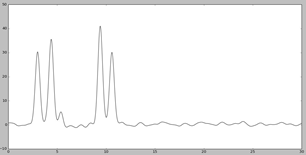
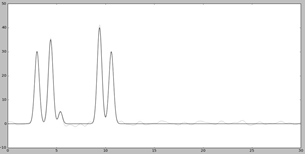
Анализируя представленные графики, можно сказать, что отличным будет качество при n₀ = 30. Можно четко отделить положение максимума всех гауссовых слагаемых функции («атомов»).

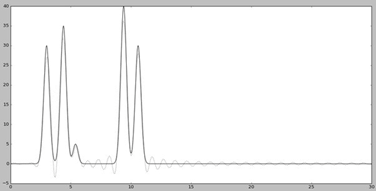
При n₀ =25 восстановление получилось хуже. Несмотря на то, что угадать положение максимумов, зная число слагаемых («атомов») можно, некоторые максимумы не отличаются от шума. Качество можно назвать хорошим.

При n₀ = 20 получили еще более худшее восстановление. Его можно оценивать как среднее, потому что положение каких-то атомов определить по восстановленной функции можно, а каких-то – нельзя.

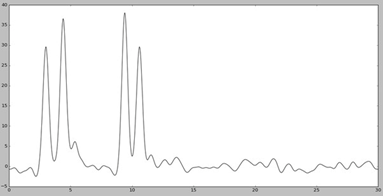
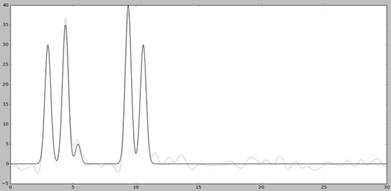
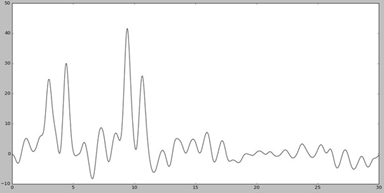
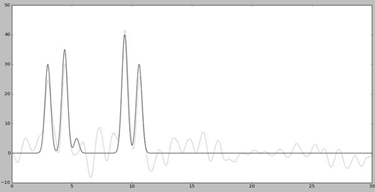
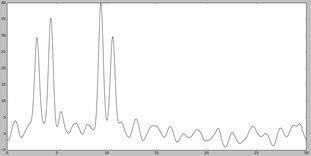
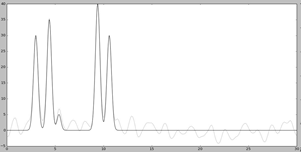
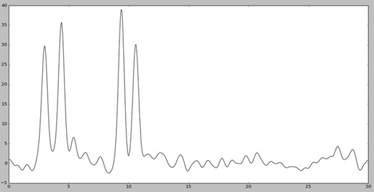
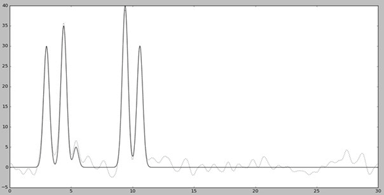
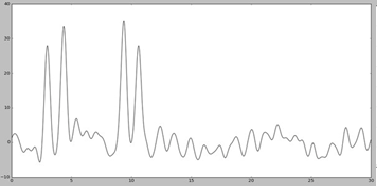
Далее для работы добавляем шум к амплитудам (параметр -F) и к фазам (параметр -Р) с помощью скрипта fourier2func.py. Графики функций с наложенным шумом представлены на Рис. 4


P=10 (без исходной функции)	P=10

P=20 (без исходной функции)	P=20

F=10 (без исходной функции)	F=10

F=20 (без исходной функции)	F=20

P=10,F=10 (без исходной функции)	P=10,F=10

P=20,F=20 (без исходной функции)	P=20,F=20

Рис. 4.Графики функций, восстановленных по n₀ = 30 с наложением шума

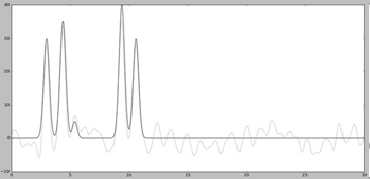Добавление шума снижает качество восстановления.

Неполный набор гармоник

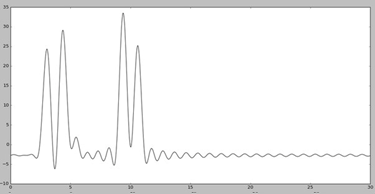
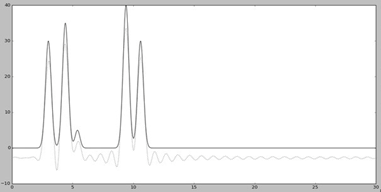
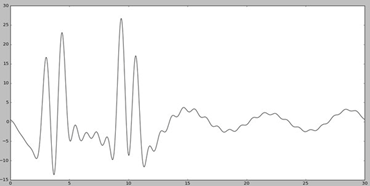
Для получения неполного набора гармоник удалили первую гармонику (Рис. 5) и первые пять гармоник (Рис. 6)

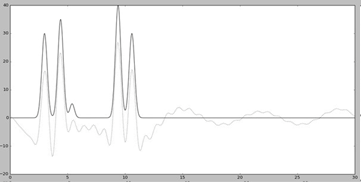Рис. 5.Графики функций, восстановленных по неполному набору гармоник без первой гармоники

Рис. 6.Графики функций, восстановленных по неполному набору гармоник без первых пяти гармоник

Анализируя Рис. 5 и Рис. 6 можно сказать, что при удалении небольшого числа гармоник качество восстановление остается прежним. Максимумы также четко различимы. Сдвиг графика на Рис. 5 образуется из-за того, что первая гармоника является константой.

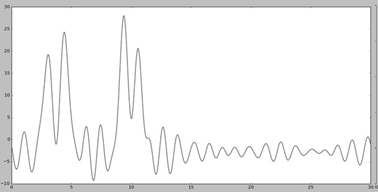
А вот удаление из середины набора (Рис. 7) привело к ухудшению восстановления.

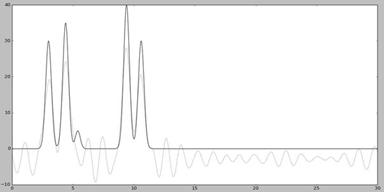Рис. 7.Графики функций, восстановленных по неполному набору гармоник
(удаление из середины набора)

При добавлении гармоники (Рис. 8) качество восстановления остается отличным.

Рис. 8.Добавление гармоники n₀ + 15

По полученным в процессе восстановления результатам была сформирована Таблица 1.

Таблица 2

Восстановление функции по коэффициентам ряда Фурье

Набор гармоник	Разрешение(Å)	Полнота данных(%)	Шум амплитуды (% от величины F)	Шум фазы (% от величины phi)	Качество восстановления (отличное, хорошее, среднее, плохое)
Полный набор гармоник
0–20	1,5	100	0	0	Среднее
0–25	1,2	100	0	0	Хорошее
0–30	1	100	0	0	Отличное
0–30	1	100	0	10	Отличное
0–30	1	100	0	20	Хорошее
0–30	1	100	10	0	Отличное
0–30	1	100	20	0	Среднее
0–30	1	100	10	10	Хорошее
0–30	1	100	20	20	Среднее
Полный набор гармоник
1–30	1	97	0	0	Отличное
5–30	1	98	0	0	Отличное
0–17,22-30	1	92	0	0	Хорошее
0–30	1	100	0	0	Отличное

Разрешением полного набора гармоник называется период гармоники с номером n (с наибольшим номером).

Период гармоники – это расстояние между соседними максимумами синусоиды (называют еще ее длиной волны, хотя физической волны нет).

Зависимость длины волны гармоники от номера:

0 – гармоника является константой
1 – длина волны равна длина отрезка Т (в нашем случае Т=30Å).