Разложение функции ЭП в ряд Фурье

Функция электронной плотности

Модель функции электронной плотности (ЭП) была создана как комбинация пяти гауссовых функций на отрезке [0; 30]. Эти пики соответствуют атомам (модель двух молекул, трехатомной и двухатомной). Расстояния между соседними пиками примерно соответствуют межатомным расстояниям внутри молекул (1.2 ангстрема) и расстоянию между молекулами в водородной связи (4 ангстрема). Таблица функции ЭП, файл func.txt, получен с помощью скрипта compile-func.py.

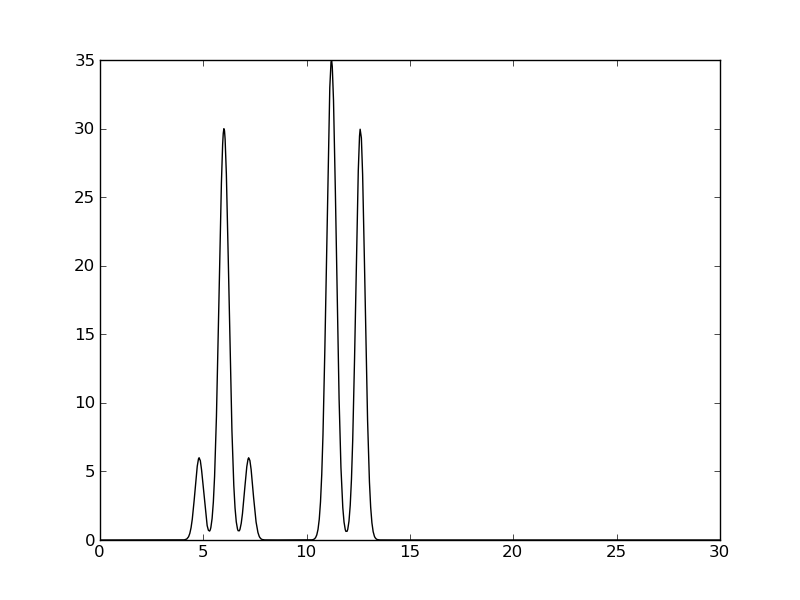
    python compile-func.py -g 6,3.5,4.8+30,3,6.0+6,3.5,7.2+35,3,11.2+30,3.2,12.6 -o func.txt

Рис. 1. Одномерная функция ЭП для трехатомной и двухатомной молекул

Прямое и обратное преобразование Фурье

Функция ЭП была разложена в ряд Фурье программой func2fourier.py, результат ее работы, файл fourier.txt, содержит 499 гармоник, где каждая гармоника описана амплитудой и фазой (только нулевая гармоника не имеет фазы по определению, использовано значение ноль для унификации):

    python func2fourier.py -i func.txt -o fourier.txt

Фунция ЭП может быть восстановлена по произвольному набору гармоник с помощью обратного преобразования Фурье. Программа fourier-filter.py позволяет выбрать набор необходимых гармоник, а программа fourier2func.py восстанавливает функцию и выводит график исходной и восстановленной функции, например:

    python fourier-filter.py -i fourier.txt -r 0-10 -o fourier-0-10.txt
    python fourier2func.py -f func.txt -i fourier-0-10.txt -o func-0-10.txt

Выбор минимального набора первых гармоник

Экспериментальные данные гармоник функции ЭП могут быть неполны и подвержены шуму. Поэтому важно знать, как эти искажения входных данных влияют на качество восстановления функции ЭП. Для оценки качества использовались следующие критерии:

Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов").
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума.
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно.
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".

Найдем минимальное число первых гармоник, которые необходимы для отличного восстановления функции, см. Рис 2.

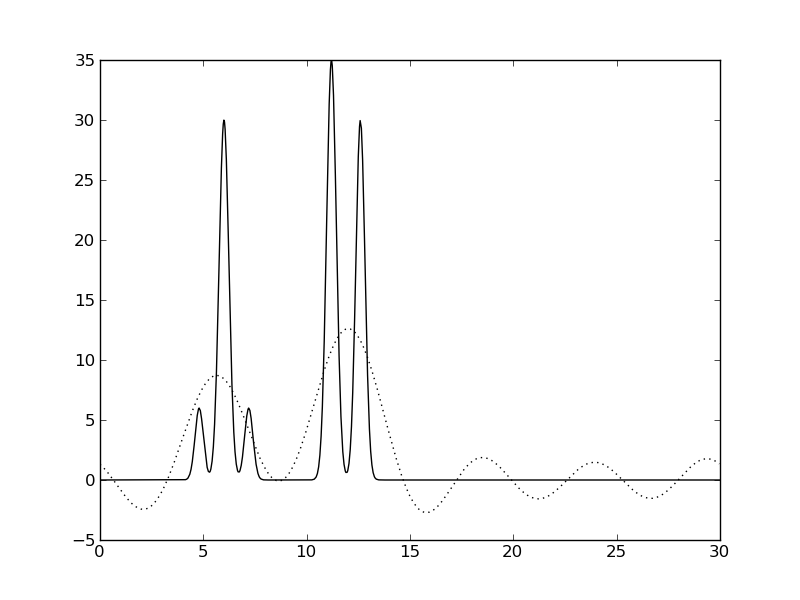
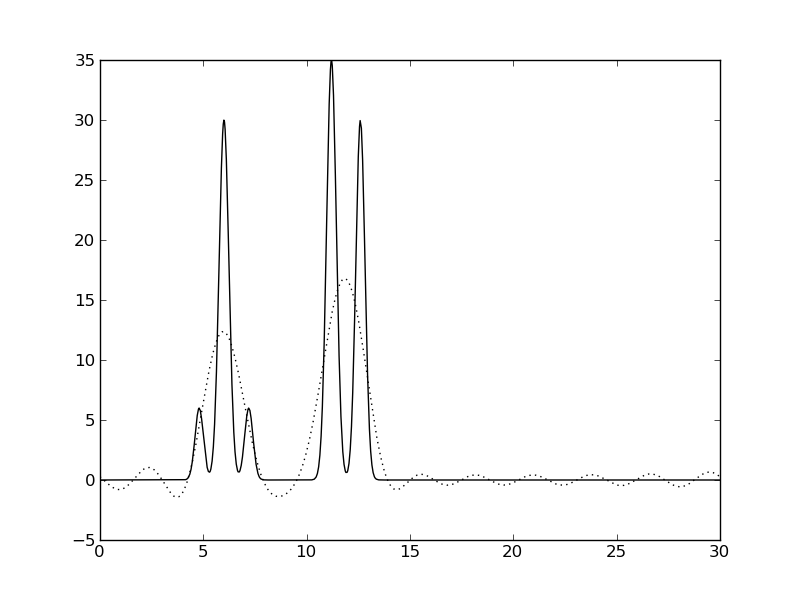
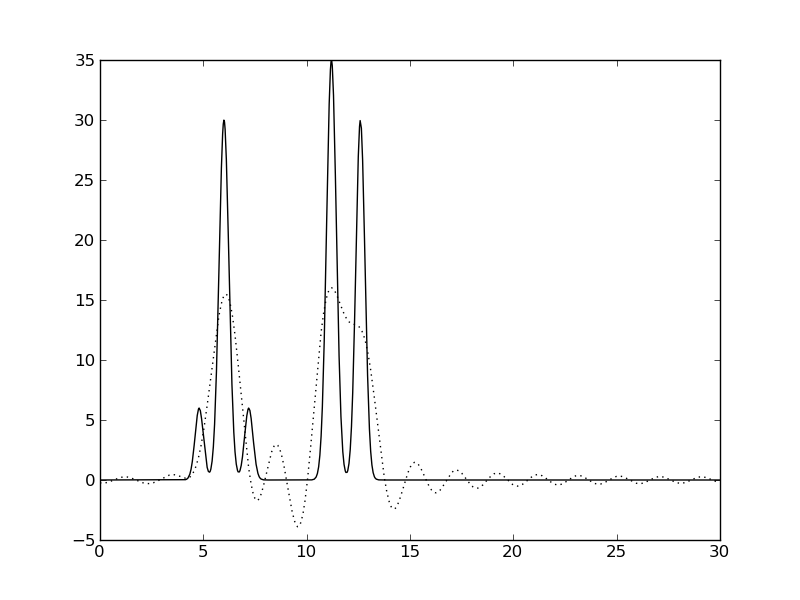
Гармоники 0-5	Гармоники 0-10	Гармоники 0-15

Гармоники 0-20	Гармоники 0-25	Гармоники 0-30

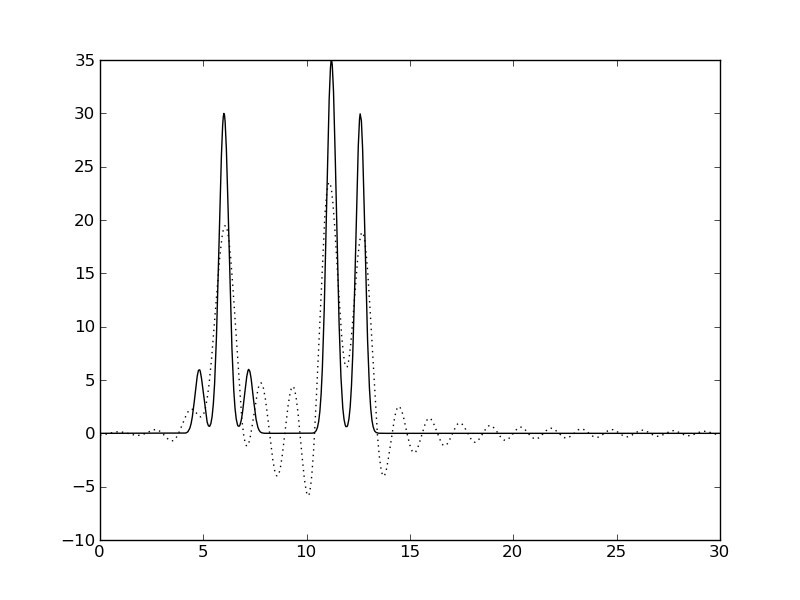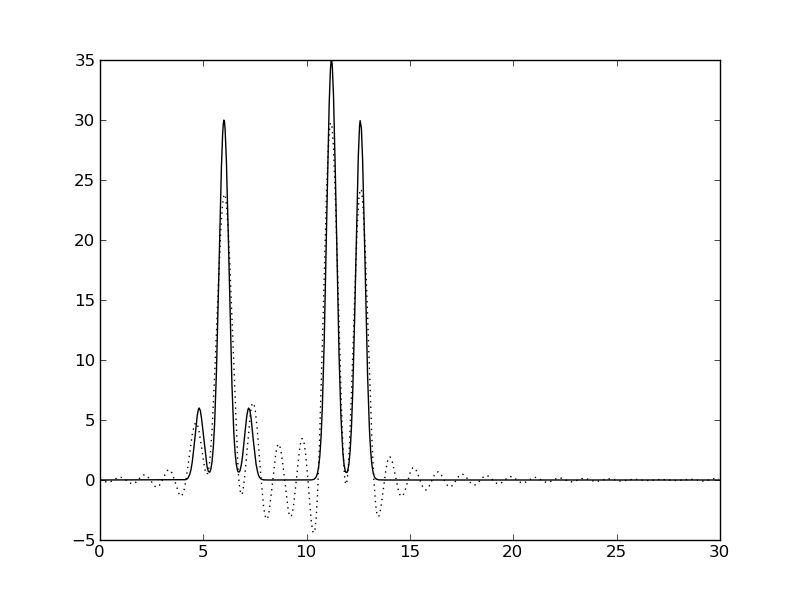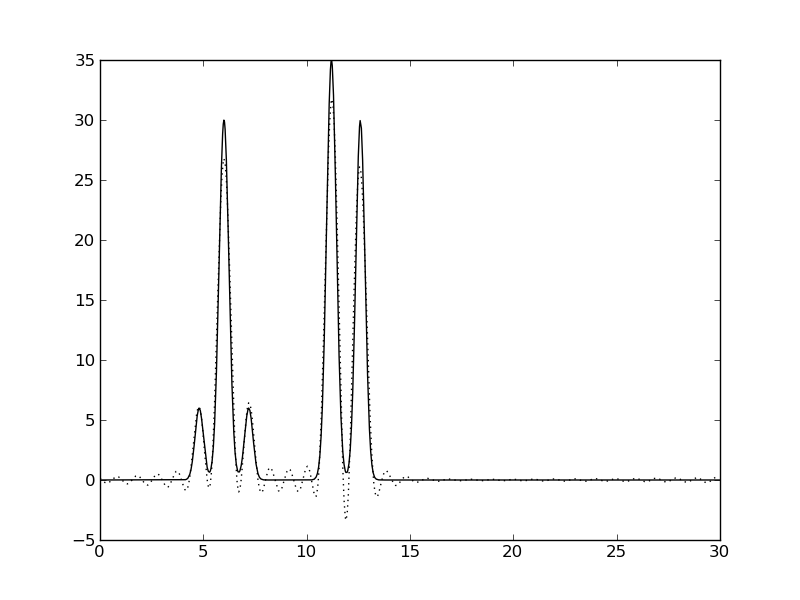Рис. 2. Восстановление функции ЭП по набору первых гармоник. Сплошная линия - исходная функция, пунктир - приближение.

Видно, что отличное качество восстановления было достигнуто только на наборе гармоник 0-30, что соответствует разрешению 1 ангстрем (примерно соответствует минимальному расстоянию между пиками функции ЭП). Это значение, n0=30, было использовано ниже для остальных экспериментов.

Влияние шума амплитуд и фаз

Программа func2fourier.py позволяет смоделировать шум для значений амплитуд (M%) и фаз (N%):

    python func2fourier.py -F M% -P N% -i func.txt -o fourier-M-N.txt

Ниже приведены результаты восстановления зашумленных гармоник с уровнями шума 0%, 10%, и 50%.

Амплитуды 0%, Фазы 0%	Амплитуды 0%, Фазы 10%	Амплитуды 0%, Фазы 50%

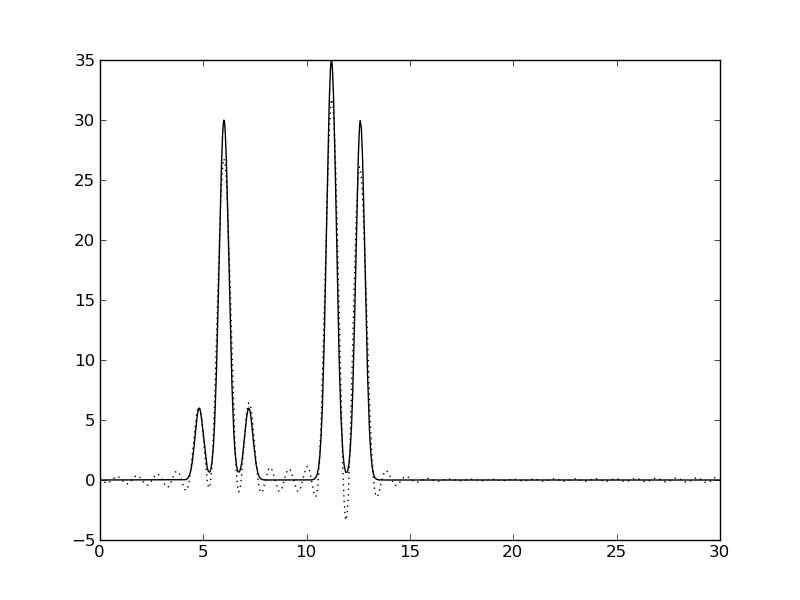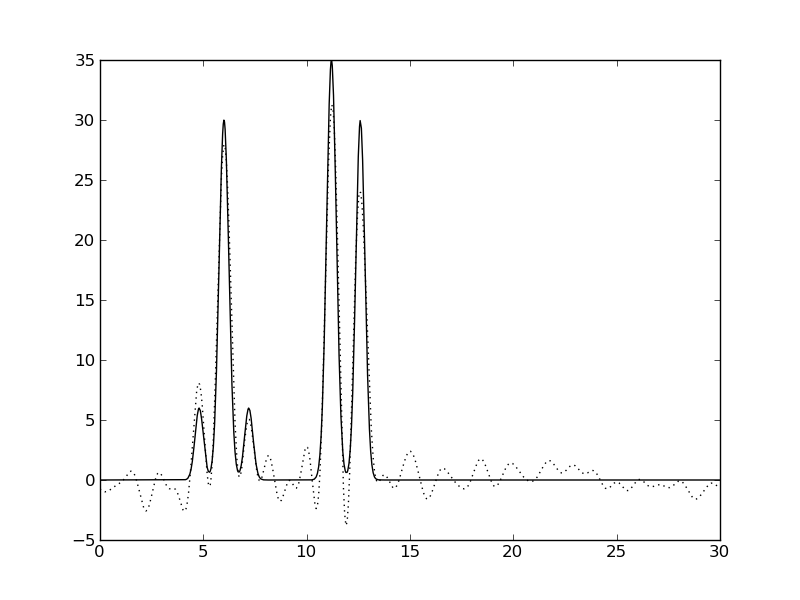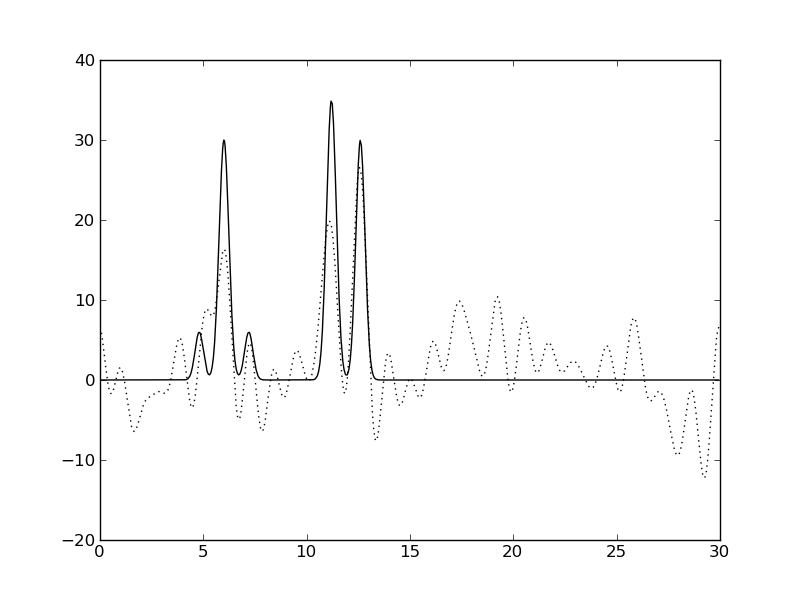Амплитуды 10%, Фазы 0%	Амплитуды 10%, Фазы 10%	Амплитуды 10%, Фазы 50%

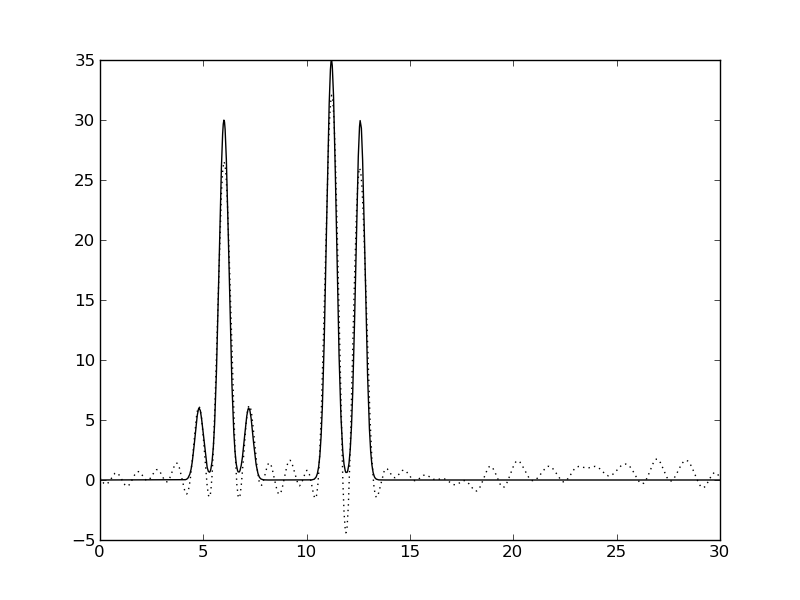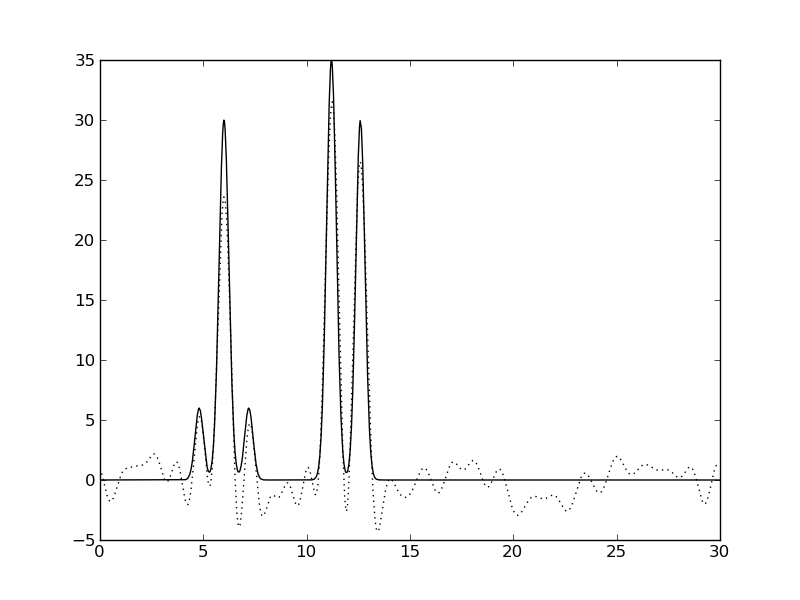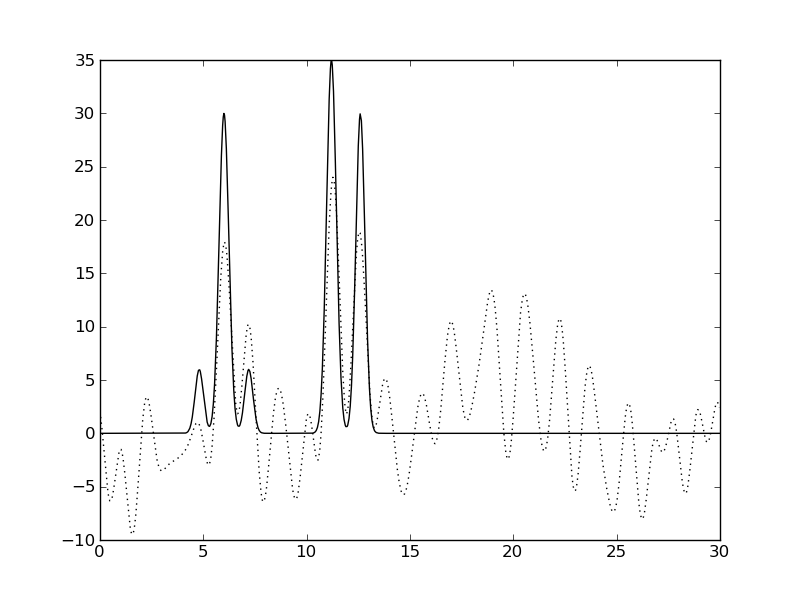Амплитуды 50%, Фазы 0%	Амплитуды 50%, Фазы 10%	Амплитуды 50%, Фазы 50%

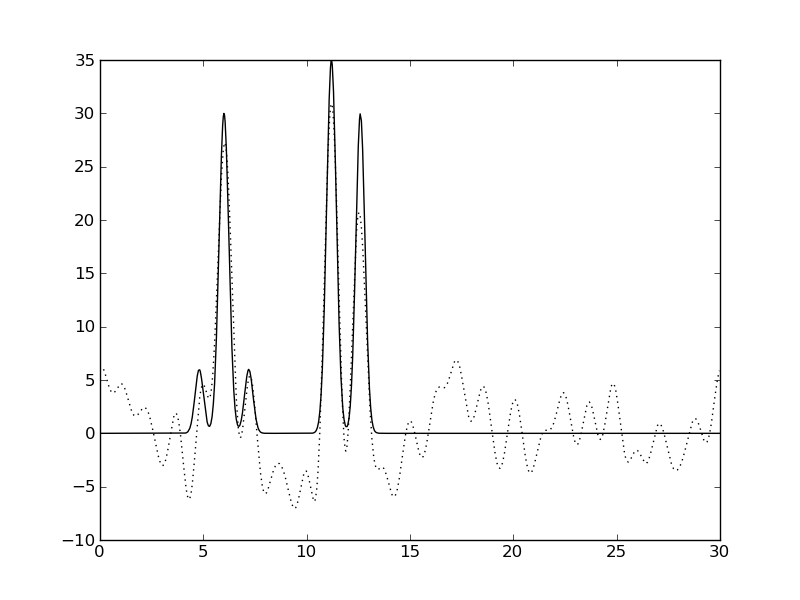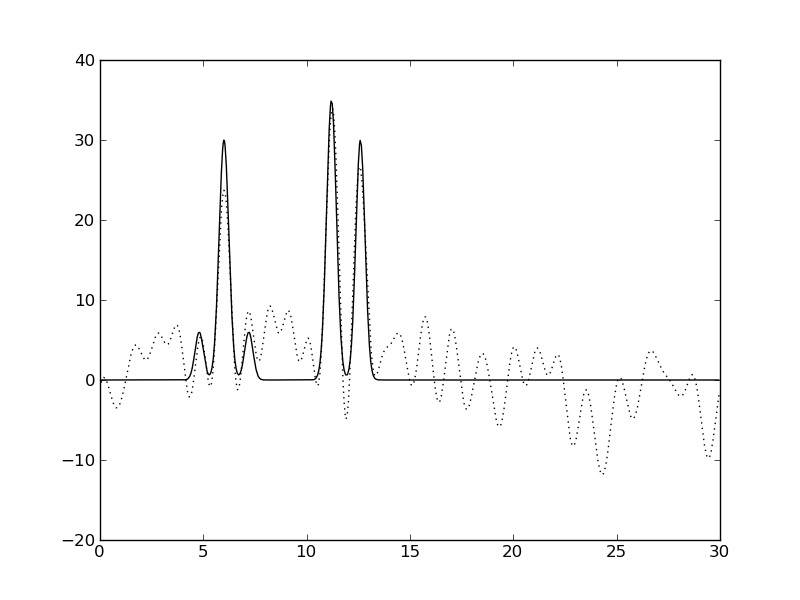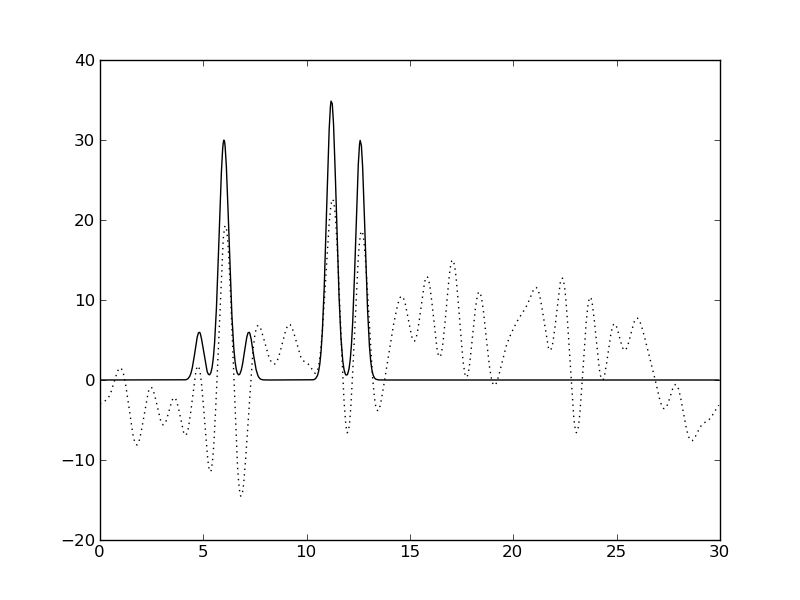Рис. 3. Влияние шума на качество восстановления функции ЭП.

Видно, что шум значений фаз сильнее ухудшает качество восстановления, чем шум амплитуд.

Восстановление по неполному набору гармоник

Для определения значимости отдельных гармоник разной частоты были также взяты несколько неполных наборов: наборы без первых одной-двух гармоник, без трех гармоник средних частот. Также тестировался расширенный набор, в котором кроме 0-30 еще добавлена гармоника 40. См. результаты на графиках Рисунка 4.

Гармоники 1-30	Гармоники 2-30

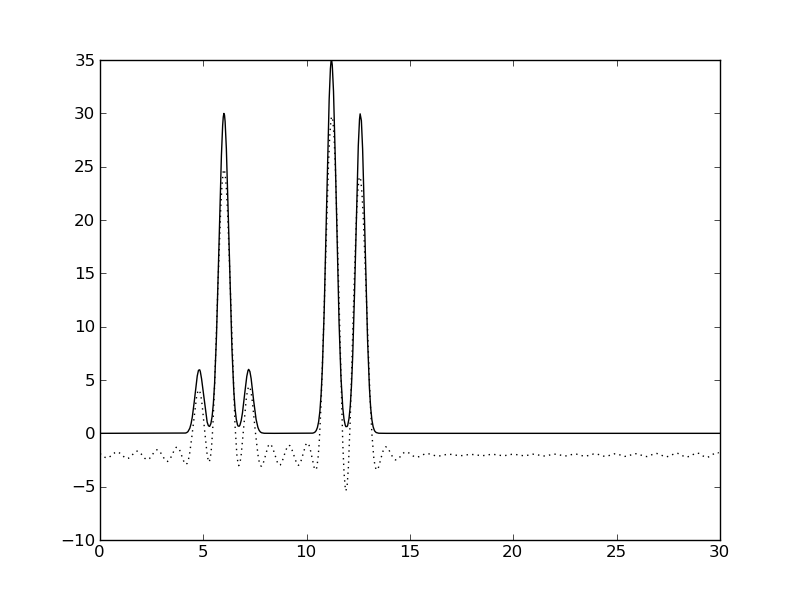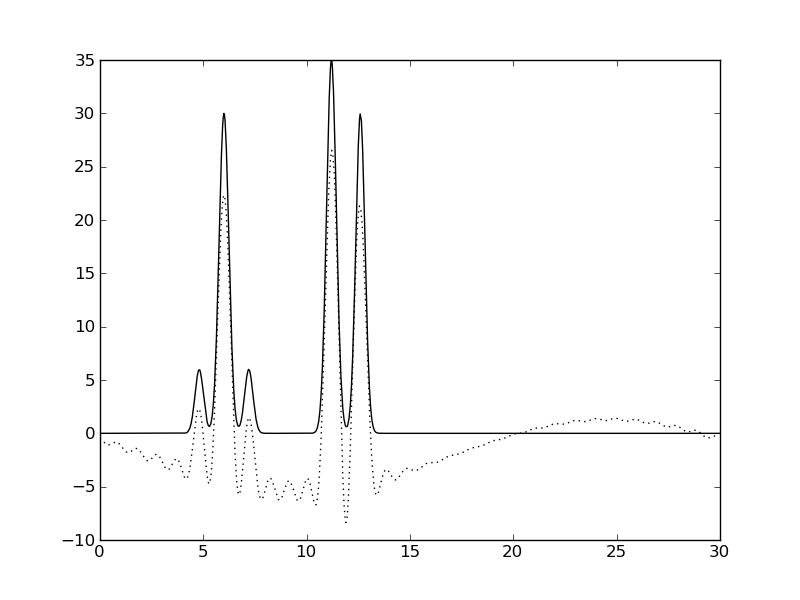Гармоники 0-11,13,15,17-30	Гармоники 0-30,40

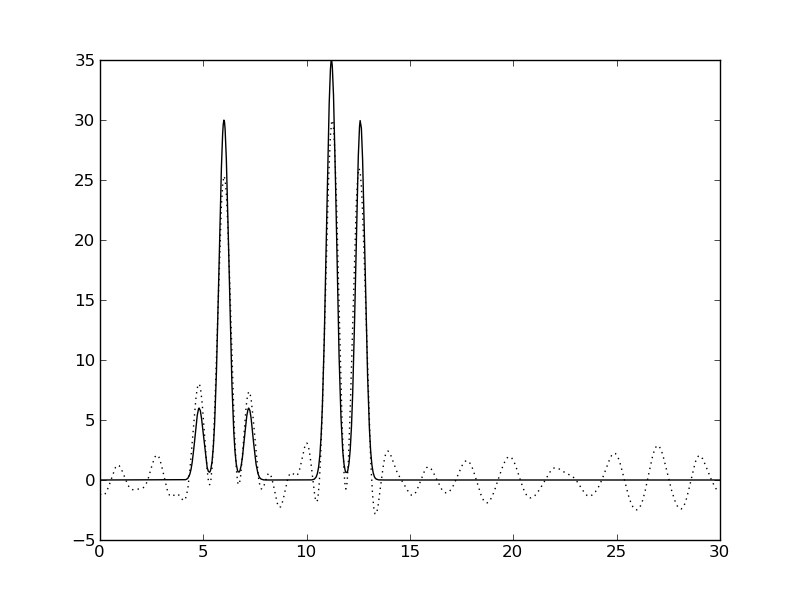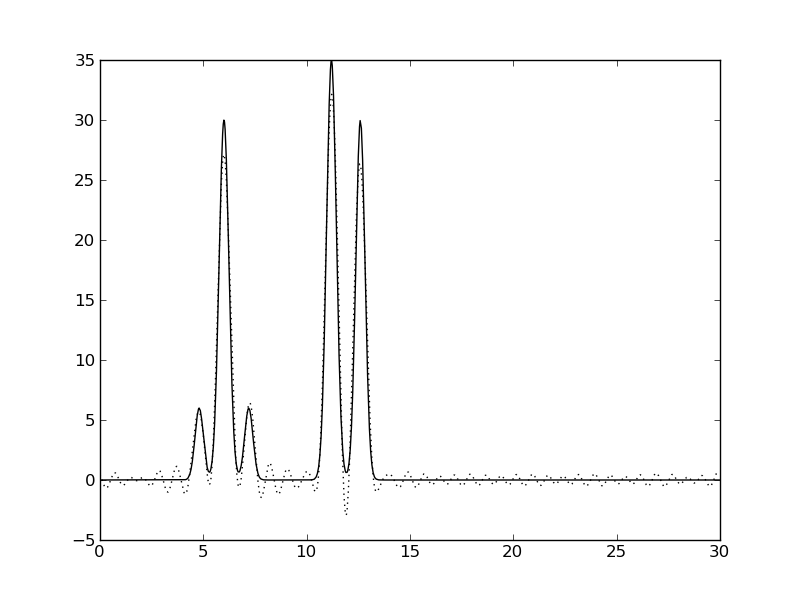Рис. 4. Восстановление по неполным наборам гармоник, добавление гармоники 40

Результаты сравнения восстановленной и исходной функций ЭП

Параметры всех вышеописанных экспериментов и оценка качества восстановления функции ЭП приведены в Таблице 1:

Таблица 1. Качество восстановления функции ЭП по неполным и зашумленным наборам гармоник.

Набор гармоник	Разрешение (Å)	Полнота данных (%)	Шум амплитуды (%F)	Шум фазы (%phi)	Качество восстановления	Комментарии
Полные наборы гармоник
0-5	6	100	0	0	плохое
0-10	3	100	0	0	плохое
0-15	2	100	0	0	плохое
0-20	1.7	100	0	0	среднее
0-25	1.2	100	0	0	хорошее
0-30	1	100	0	0	отличное	значение 30 было выбрано как n0
0-30	1	100	10	0	отличное
0-30	1	100	50	0	среднее
0-30	1	100	0	10	хорошее
0-30	1	100	0	50	плохое
0-30	1	100	50	10	среднее
0-30	1	100	10	50	плохое
0-30	1	100	10	10	хорошее
0-30	1	100	50	50	плохое
Неполные наборы гармоник
1-30	1	96.7	0	0	отличное	функция смещена по-вертикали
2-30	1	93.5	0	0	хорошее	функция смещена и искажена синусоидой
0-11,13,15,17-30	1	90.3	0	0	хорошее	функция зашумлена, но пики ЭП различимы
0-30,40	1	100	0	0	отличное	нет видимых преимуществ перед набором 0-30