Задание функции. Рассчет амплитуд и фаз сигналов, моделирующих экспериментальные данные.
В данном практикуме нужно было исследовать качество восстановления функции электронной плотности (ЭП) в зависимости от того, какие и сколько измеренных гармоник ряда Фурье используется для её восстановления.

Функция ЭП для двух молекул из двух и трех атомов была построена при помощи скрипта compile-func.py следующей командой:

python compile-func.py -g 32,3,7.6+12,3,9.1+16,3,3.2+2,3.5,7+34,3,8

Соответственно, максимумы гауссовых функций в точках 6, 1, 2, 7 и 8 и высотой 32, 12, 16, 2 и 34. В качестве результата скрипт выдал файл - func.txt. График функции ЭП изображён на Рисунке 1 ниже.


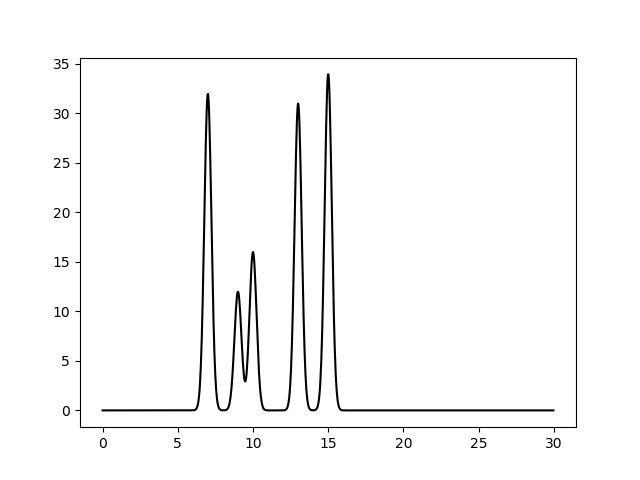
Рисунок 1.График функции ЭП на интервале [0,30] для системы из двух молекул, состоящих из 2 и 3 атомов.

Полученная функция была разложена в ряд Фурье с использованием скрипта func2fourier.py и команды:

python func2fourier.py -i func.txt.

В итоге, был получен файл func_ft.txt, содержащий 499 гармоник, которые в сумме дают исходную функцию. В файле func_ft.txt первый столбец соответствует номеру гармоники, второй - амплитуда (P), третий - фазе (phi).

Восстановление функции ЭП по модельным ("экспериментальным") данным.
Cкриптом fourier-filter.py отбиралось необходимое число гармоник (первые 10, 20, 30 и 40), по которым с помощью скрипта fourier2func.py восстанавливалась функция: (в случае для 10)

python fourier-filter.py -i func_ft.txt -r 0-10 -o func_ft_0_10.txt
python fourier2func.py -f func.txt -i func_ft_0_10.txt -o 0_10_func.txt


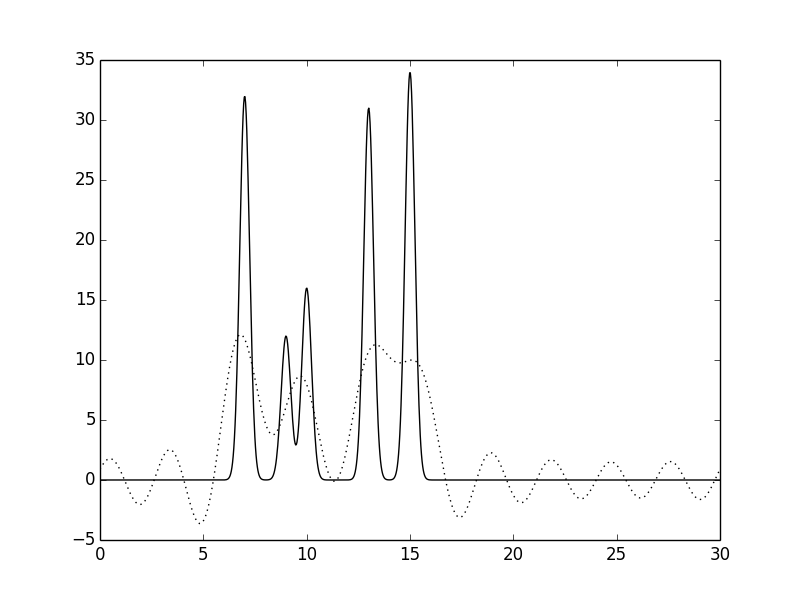
Рисунок 2.Функции электронной плотности, восстановленные по первым 10 гармоникам.


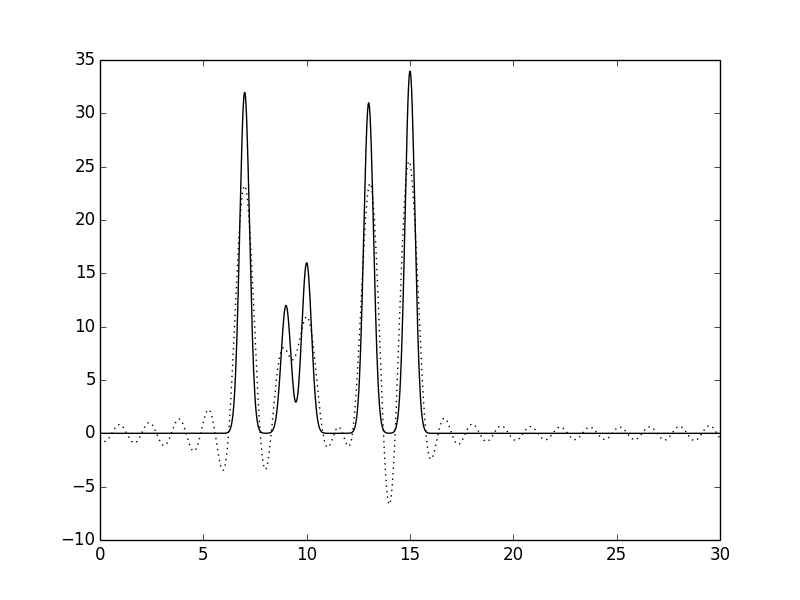
Рисунок 3.Функции электронной плотности, восстановленные по первым 20 гармоникам.


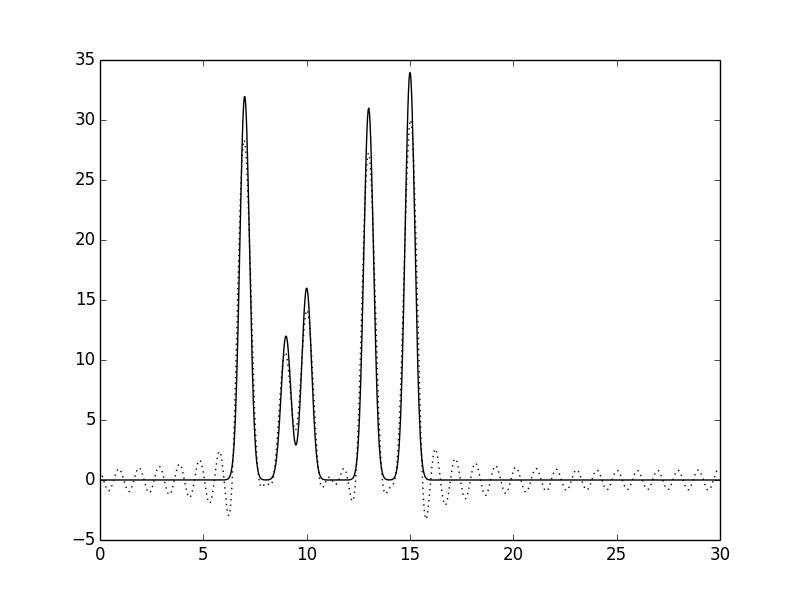
Рисунок 4.Функции электронной плотности, восстановленные по первым 30 гармоникам.


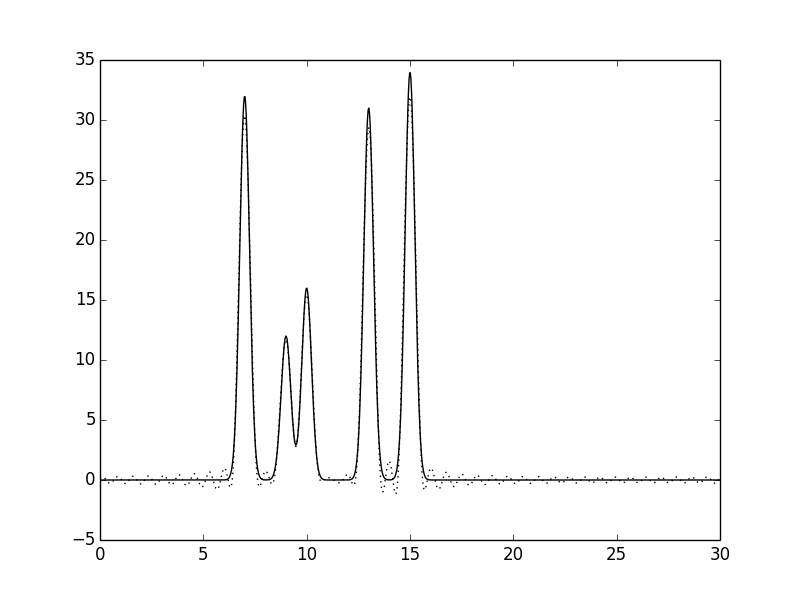
Рисунок 5.Функции электронной плотности, восстановленные по первым 40 гармоникам.


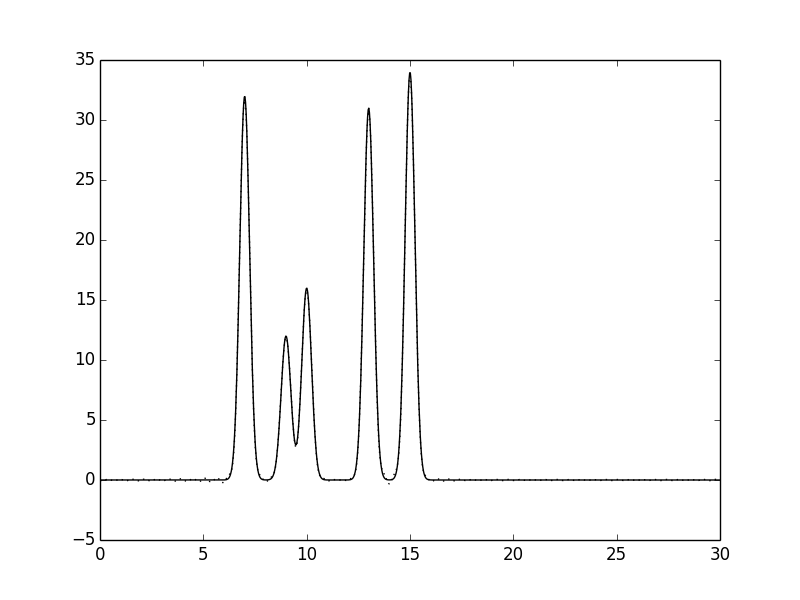
Рисунок 6.Функции электронной плотности, восстановленные по первым 50 гармоникам.

По рисункам видно, что по 30 гармоникам уже можно точно определить положения атомов в молекулах. Поэтому для дальнейших расчетов использовался набор из 0-30 гармоник.

Далее в расчет коэффициентом фурье был добавлен шум к амплитудам или фазам (параметры –F и –P скрипта func2fourier.py) при n=30: (Например, для F=20% и P=20%)

python func2fourier.py -F 20 -P 20 -i func_ft.txt -o ft_noise20-20.txt
python fourier-filter.py -r 0-30 -i ft_noise20-20.txt -o ft_noise20-20_n0.txt
python fourier2func.py -i ft_noise20-20_n0.txt -o two_func_noise20-20_n0.txt


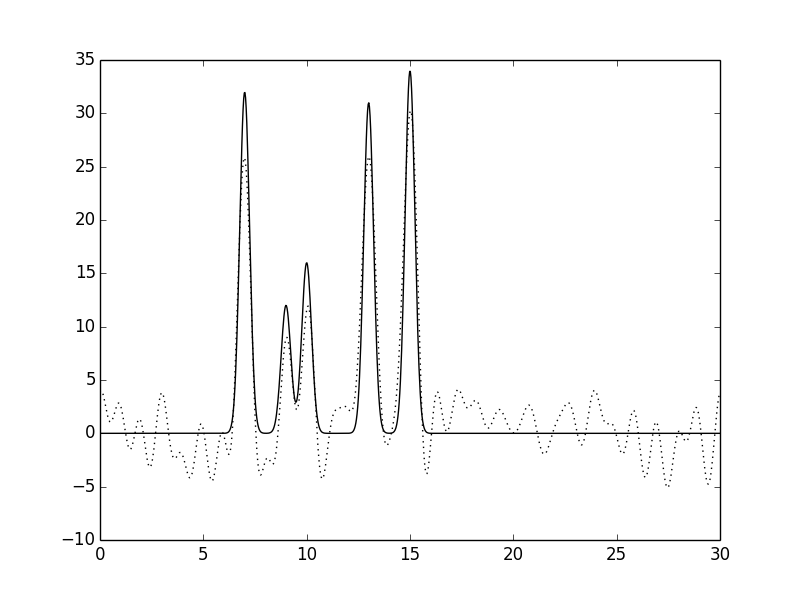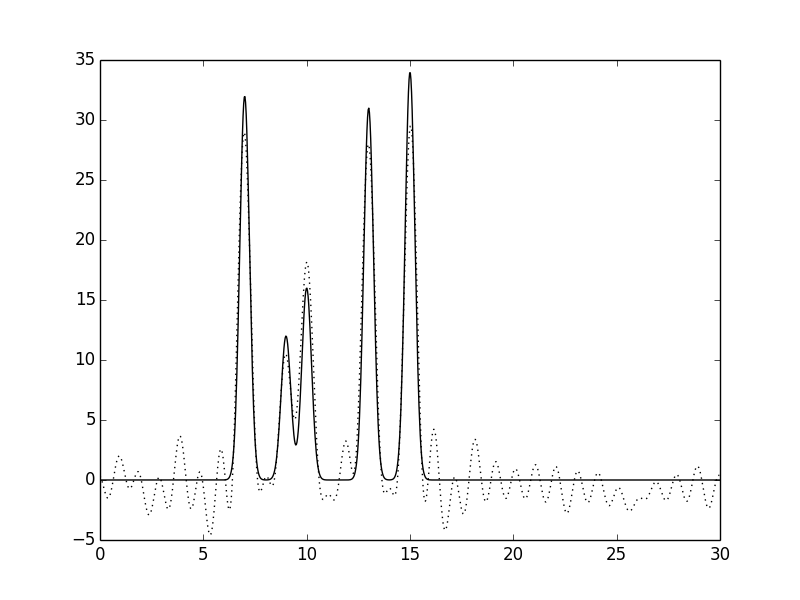
Рисунок 7.Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 20% шума к фазам (слева) или к амплитудам (справа).



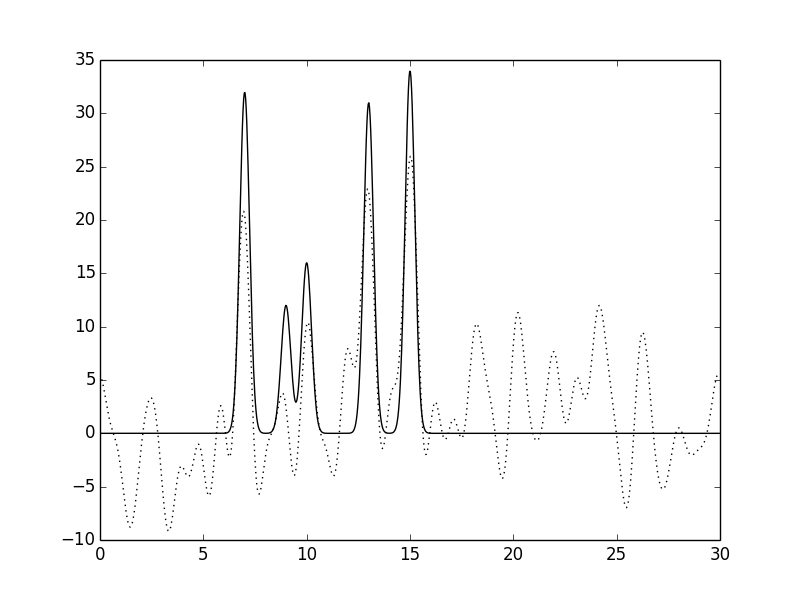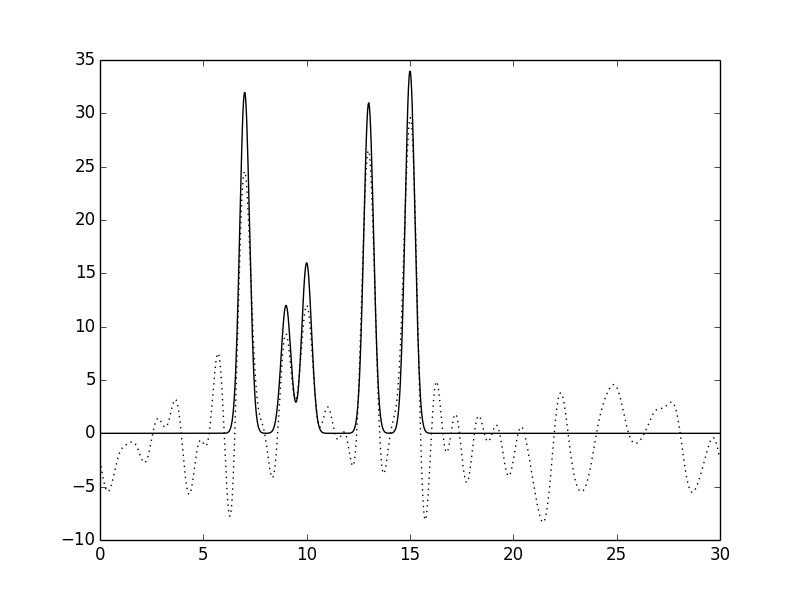
Рисунок 8.Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 40% шума к фазам (слева) или к амплитудам (справа).



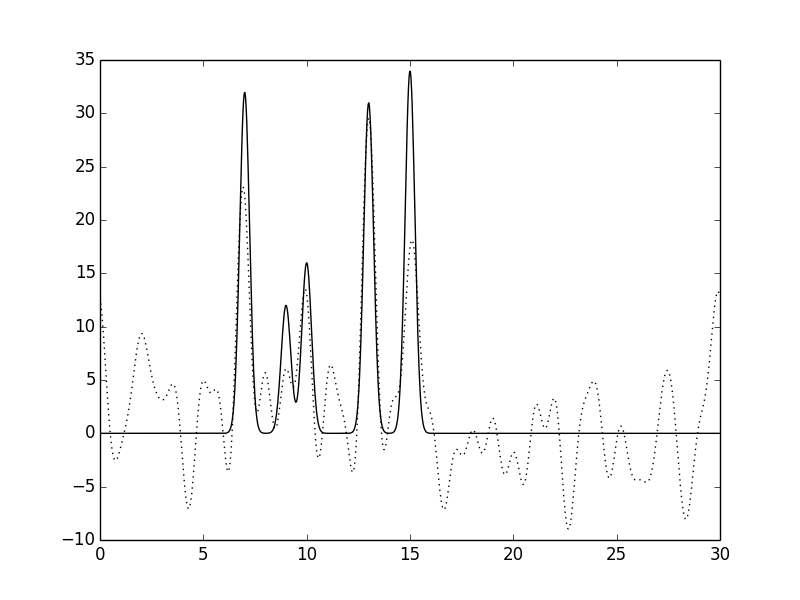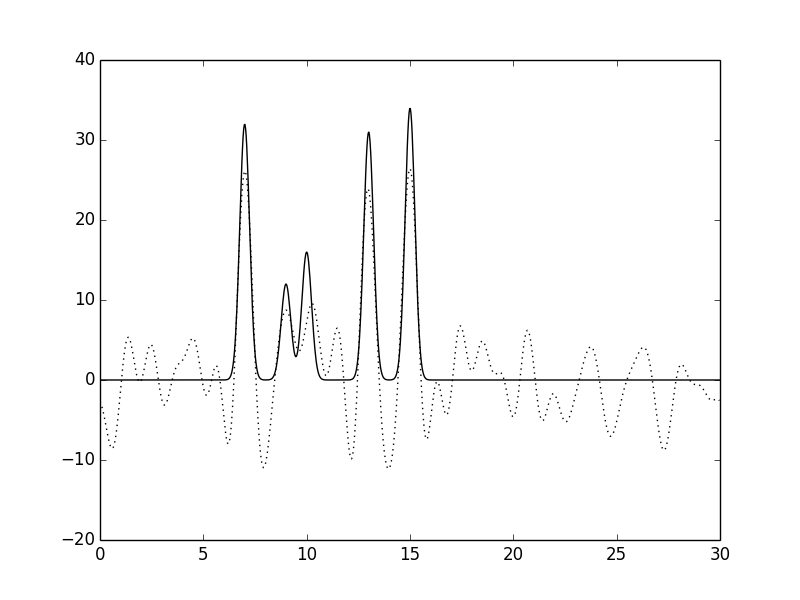
Рисунок 9.Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 60% шума к фазам (слева) или к амплитудам (справа).



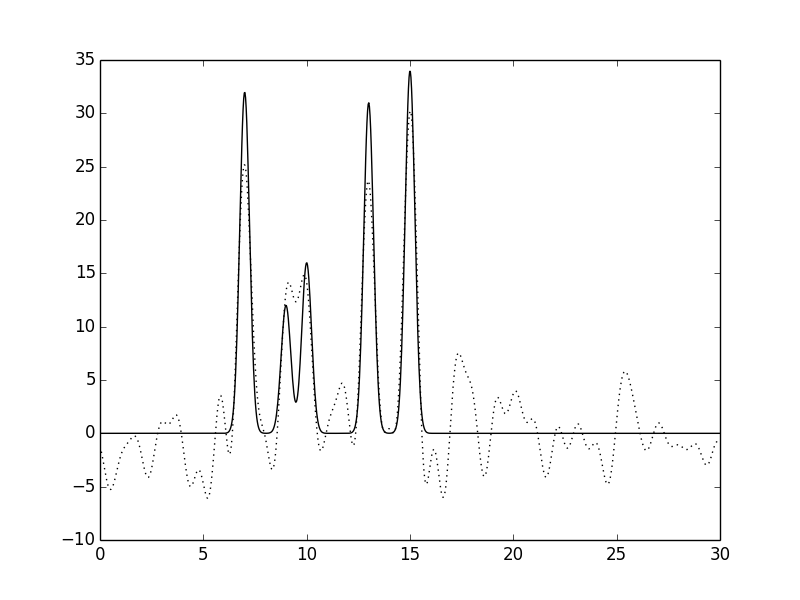
Рисунок 10.Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 20% шума к фазам и к амплитудам.



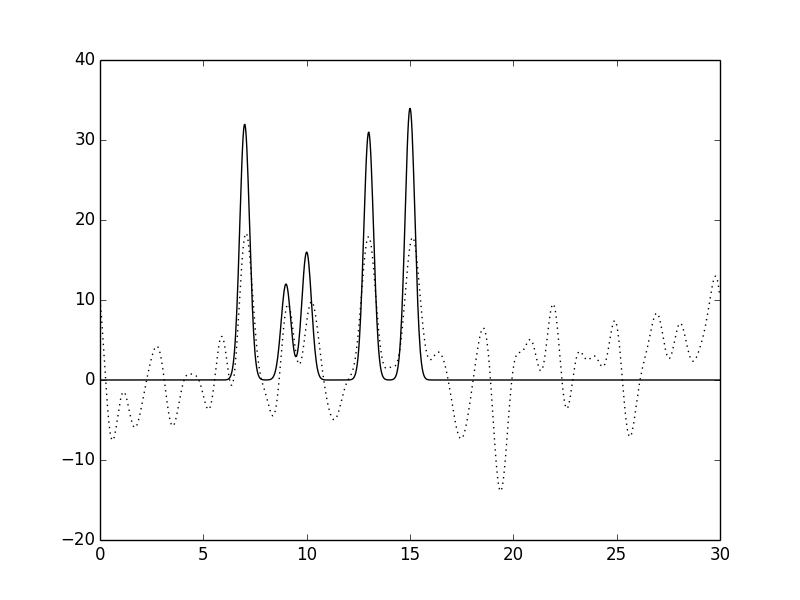
Рисунок 11.Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 40% шума к фазам и к амплитудам.



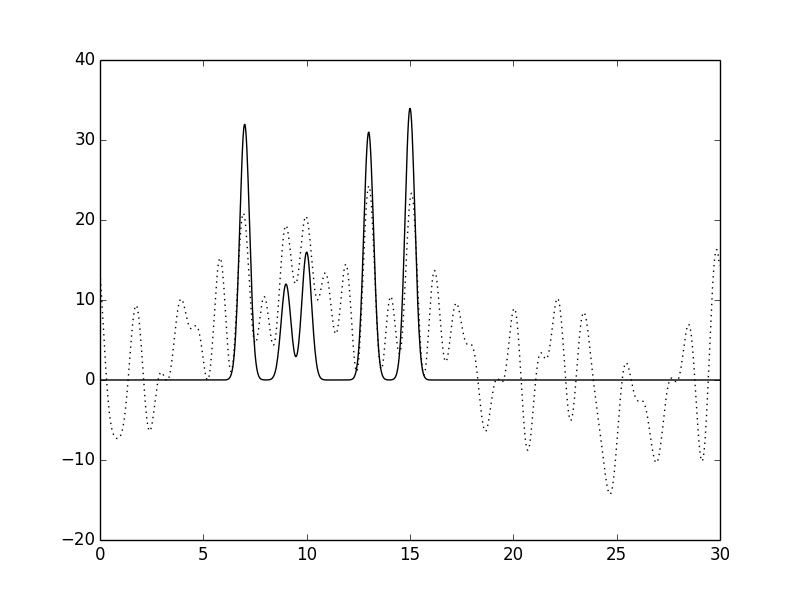
Рисунок 12.Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 60% шума к фазам и к амплитудам.



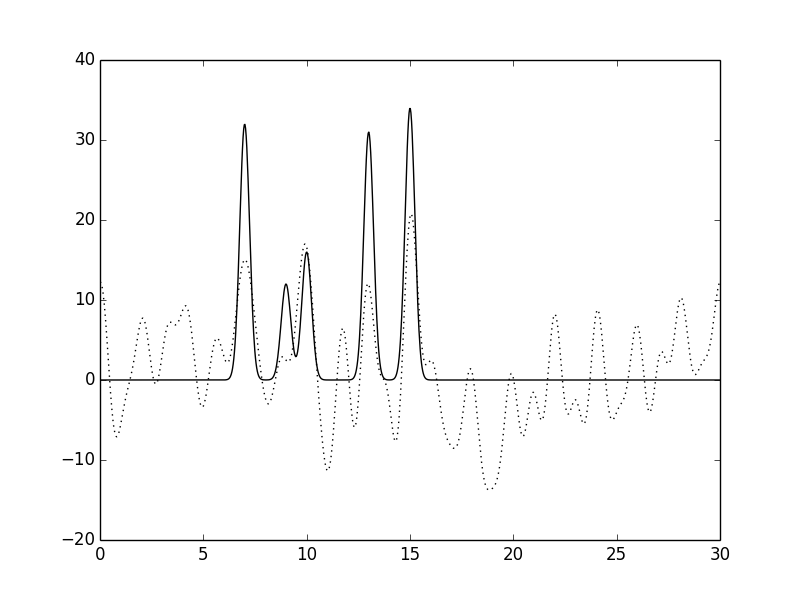
Рисунок 13.Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 20% шума к амплитудам и 60% к фазам.



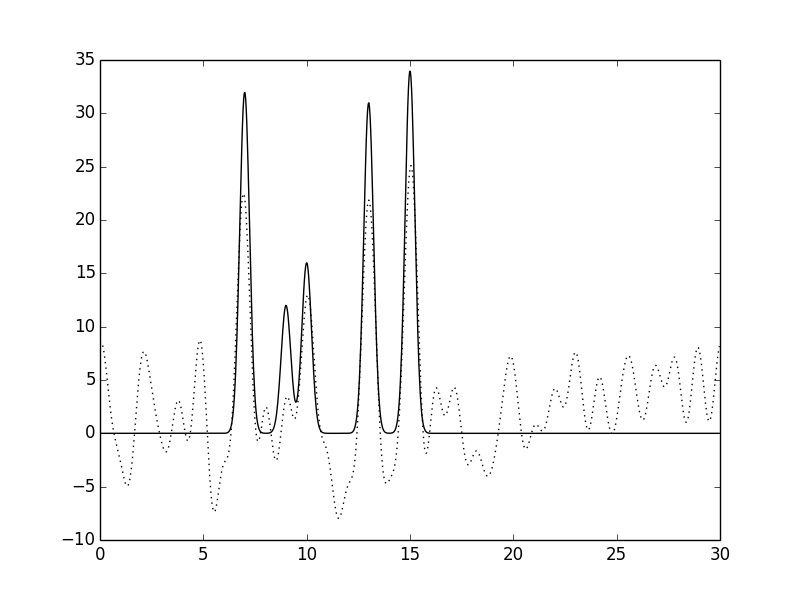
Рисунок 14.Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 60% шума к амплитудам и 20% к фазам.


Особенно по 13 и 14 рисункам видно, что увеличение степени шума по амплитудам не приводит к существенным изменениям вида функции электронной плотности.

Для реального эксперимента не всегда удается измерить все амплитуды и фазы ряда Фурье. Рассмотрим восстановление функции ЭП по неполным наборам гармоник.

Для получения неполного набора гармоник было удалено несколько начальных гармоник:

python fourier-filter.py -r *-35 -i func.txt -o ft_*-35.txt
python fourier2func.py -i ft_*-35.txt -o two_func_*-35.txt


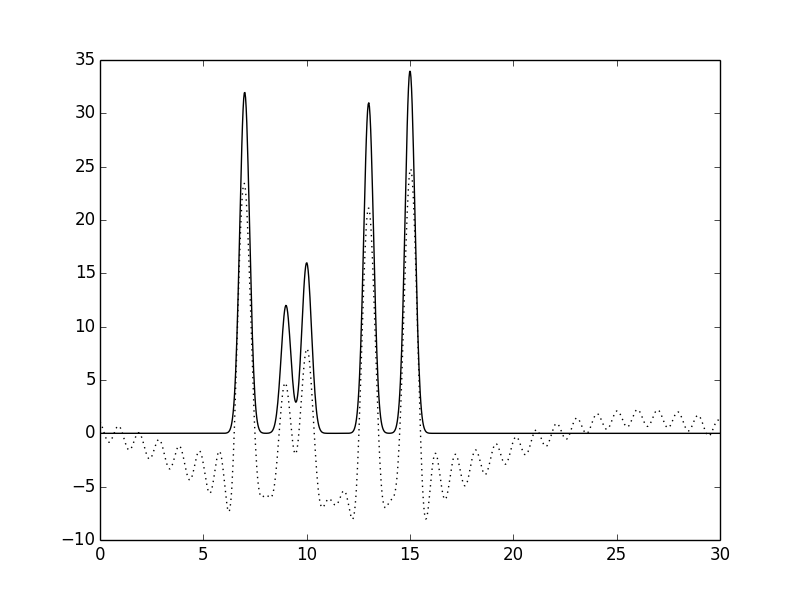
Рисунок 15.Функция электронной плотности, восстановленная по наборам гармоник 2-30.



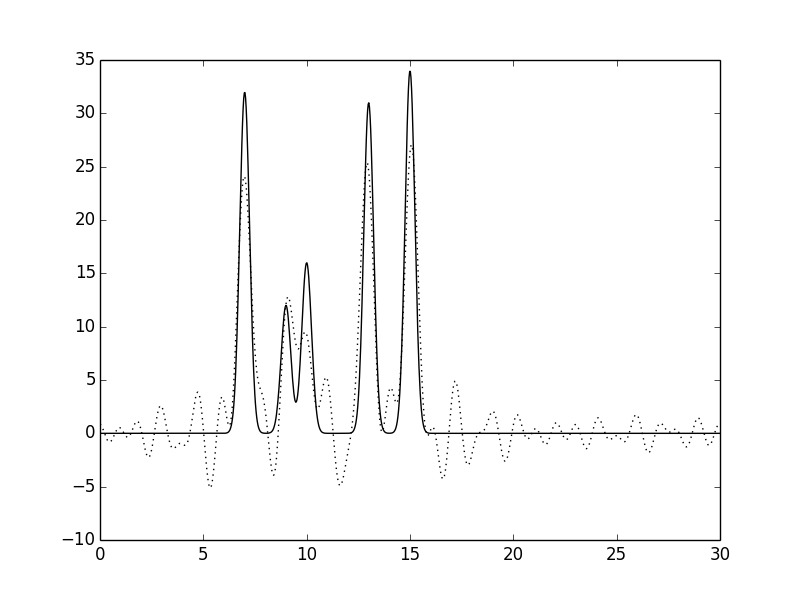
Рисунок 16.Функция электронной плотности, восстановленная по наборам гармоник 0-17, 21-30.



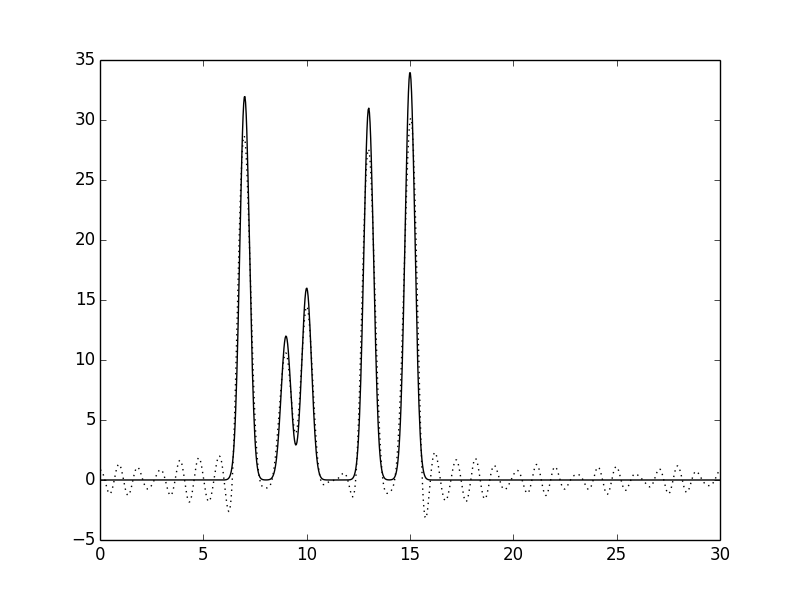
Рисунок 17.Функция электронной плотности, восстановленная по наборам гармоник 0-30, 40.