Сравнение множественных выравниваний

Задание 1

Я написала скрипт для сравнения двух множественных выравниваний. Инструкция вызывается командой python msa.py -h.

Задание 2

Я решила выравнивать домен 10 кДа шаперонина PF00166, с которым я работала в предыдущих практикумах. Я открыла выравнивание seed в Jalview, удалила из него гэпы и выровняла там же тремя программами: Clustal Omega, Mafft и Muscle (проект Jalview). Результаты сравнения трех выравниванием с проверенным людьми выравниванием seed представлены в Таблице 1. Наиболее близким к референсному оказалось выравнивание Clustal Omega c процентом совпадающих колонок немногим более 50. Также можно заметить, что для трех пар выравниваний границы идентичных блоков примерно совпадают, что позволяет нам судить о достоверности выравнивания в этих блоках.

Таблица 1. Результаты сравнения выравниваний с выравниванием Seed
Выравнивание 1 Длина выравнивания 1 Выравнивание 2 Длина выравнивания 2 Количество идентичных колонок Процент идентичных колонок от длины выравнивания 1 Процент идентичных колонок от длины выравнивания 2 Координаты идентичных блоков* Координаты одиночных идентичных колонок**
Seed 121 Clustal Omega 115 62 51.2% 53.9%
  • 1,13=1,13
  • 21,31=21,31
  • 45,54=42,51
  • 74,83=69,78
  • 91,94=87,90
  • 109,121=103,115
 15,15
Seed 121 Mafft 120 56 46.3% 46.7%
  • 1,11=1,11
  • 24,30=24,30
  • 45,52=42,52
  • 74,83=72,81
  • 90,94=88,92
  • 108,121=107,120
 32,32
Seed 121 Muscle 114 49 40.5% 43.0%
  • 1,11=1,11
  • 22,31=22,31
  • 45,53=42,50
  • 90,92=85,87
  • 95,96=90,91
  • 109,121=102,114
 17,17
*До знака "равно" координаты начала и конца блока в выравнивании 1, после — в выравнивании 2.
**Координата в выравнивании 1, координата в выравнивании 2.

Далее я сравнила выравнивания Clustal Omega, Mafft и Muscle между собой. Результаты можно видеть в Таблице 2. Наиболее схожи между собой выравнивания, полученные программами Clustal Omega и Mafft (59.1% и 56.7% идентичных колонок от длин выравниваний Clustal Omega и Mafft соответственно).

Таблица 2. Результаты попарного сравнения выравниваний
Выравнивание 1 Длина выравнивания 1 Выравнивание 2 Длина выравнивания 2 Количество идентичных колонок Процент идентичных колонок от длины выравнивания 1 Процент идентичных колонок от длины выравнивания 2 Координаты идентичных блоков* Координаты одиночных идентичных колонок
Clustal Omega 115 Mafft 120 68 59.1% 56.7%
  • 1,11=1,11
  • 24,30=24,30
  • 42,49=45,52
  • 65,83=68,86
  • 87,96=89,98
  • 103,115=108,120
 —
Clustal Omega 115 Muscle 114 54 47.0% 46.4%
  • 1,11=1,11
  • 22,35=22,35
  • 38,50=38,50
  • 87,88=86,87
  • 102,115=101,114
 —
Mafft 120 Muscle 114 43 35.8% 37.7%
  • 1,12=1,12
  • 24,30=24,30
  • 45,52=42,49
  • 88,90=85,87
  • 108,120=102,114
 —
*До знака "равно" координаты начала и конца блока в выравнивании 1, после — в выравнивании 2.

Задание 3

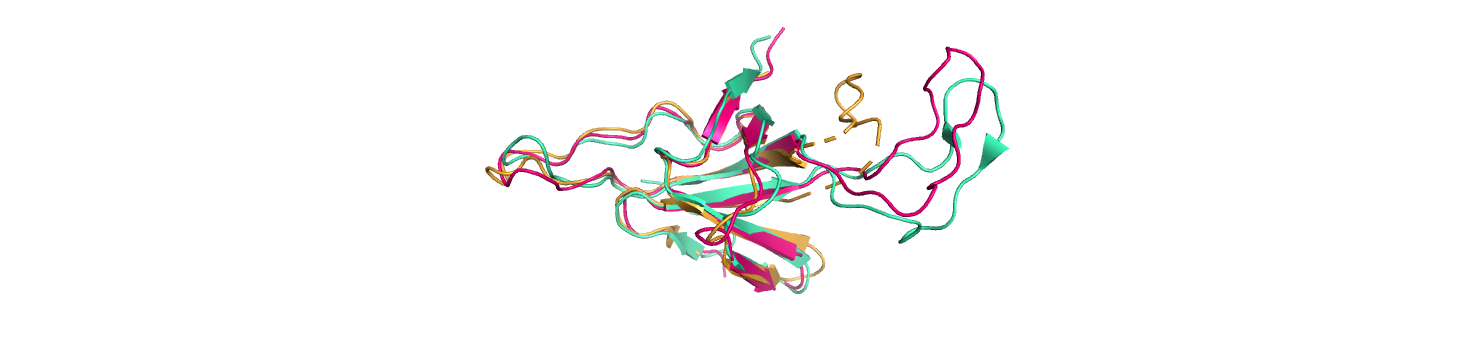
Я выбрала следующие структуры, содержащие исследуемый мной домен: 1AON (цепь O, E. coli), 4PJ1 (цепь O, Homo sapiens) и 1HX5 (цепь A, Mycobacterium tuberculosis). Я создала структурное выравнивание (Рис. 1) в PyMol, взяв структуру 1AON за референсную. Затем экспортировала выравнивание последовательностей, полученное из выравнивания структур, и визуализировала его в Jalview вместе с выравниванием тех же последовательностей программой Clustal Omega (проект). Результаты сравнения этих выравниваний с помощью моей программы отражены в Таблице 3. Выравнивания отличаются примерно на столько же, на сколько различаются множественные выравнивания последовательностей, полученные с помощью разных программ. При этом видно, что выравнивание структур имеет значительно большую длину и, следовательно, подразумевает больше событий образования инделей.

structures
Рисунок 1. Выравнивание структур. Розовая цепь — 1AON, циановая — 4PJ1, оранжевая — 1HX5.
Таблица 3. Результаты сравнения выравнивания структур с выравниванием последовательностей
Выравнивание 1 Длина выравнивания 1 Выравнивание 2 Длина выравнивания 2 Количество идентичных колонок Процент идентичных колонок от длины выравнивания 1 Процент идентичных колонок от длины выравнивания 2 Координаты идентичных блоков* Координаты одиночных идентичных колонок**
Structure 155 Clustal Omega 116 68 43.9% 58.6%
  • 13,22=11,20
  • 65,77=42,54
  • 92,104=63,75
  • 112,117=80,85
  • 122,133=88,99
  • 139,150=105,116
  • 82,57
  • 87,61
*До знака "равно" координаты начала и конца блока в выравнивании 1, после — в выравнивании 2.
**Координата в выравнивании 1, координата в выравнивании 2.

Задание 4

Clustal Omega — опубликованная в 2011 году программа множественного выравнивания белковых последовательностей. Она относится к быстрым, обладает высокой точностью и позволяет создавать выравнивания более 10 тыс. последовательностей. Она осуществляет построение направляющего дерева не в результате попарного выравнивания всех последовательностей (сложность алгоритма N*N, где N — число последовательностей), а на основе подсчета расстояний каждой последовательности до референсных (их количество пропорционально logN, сложность алгоритма N*logN). Затем последовательности выравниваются по профилям Скрытых марковских моделей (HMM). У этой программы есть функции добаления новых последовательностей к выравниванию и использования существующих профилей НММ (например, указываются в записях Pfam) для выравнивания гомологичных последовательностей.

Источник: Sievers F, Wilm A, Dineen D, Gibson TJ, Karplus K, Li W, Lopez R, McWilliam H, Remmert M, Söding J, Thompson JD, Higgins DG. Fast, scalable generation of high-quality protein multiple sequence alignments using Clustal Omega. Mol Syst Biol. 2011 Oct 11;7:539.