Восстановление электронной плотности с помощью ряда Фурье


Работа проводилась на модели из двух гипотетеических молекул. Модель была создана с помощью скрипта compile-func, который моделирует функцию электронную плотность в зависимости от заданных параметров. В данном случае модель описывалась следующими параметрами:

    
 
  1. Электронная плотность для каждого атома задается Гауссовой функцией с параметрами высоты (число электронов), ширины (радиус атома) и точки максимума (координата атома).
    2.  
 
  2. Общая шкала 30 Å.
    3. 
 
  3. Расстояние между молекулами около 5 Å (примерно соотвествует длине водородной связи).
    4. 
 
  4. Одна молекула трехатомная, вторая - двухатомная.
    5. 


Модель была создана следующей командой:

 compile_func.py -g 20,5,4+40,3,5+20,5,6+10,4.2,10+30,4.7,10.7 

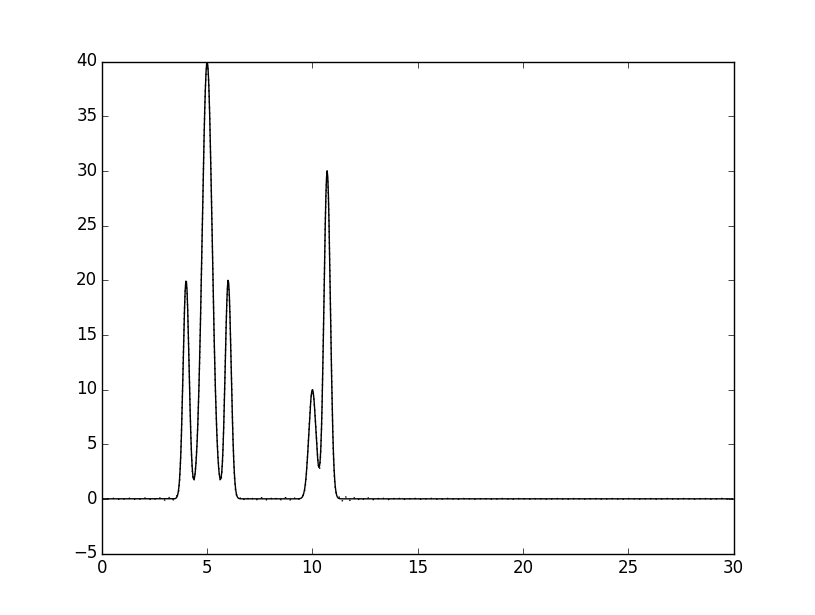
Был получен файл со значениями и графическое изображение ЭП модели:




 

 
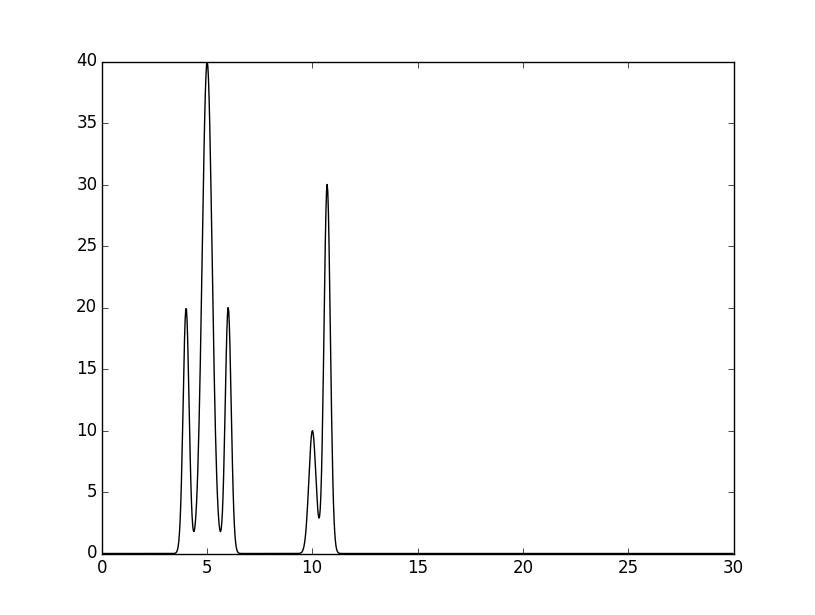Рисунок 1.Модель электронной плотности для двух молекул.




Затем с помощью скрипта func2fourier функция была разложена в ряд Фурье. Было получено 500 гармоник (0-499), их коэффициенты (фазы и амплитуды) записаны в файл.


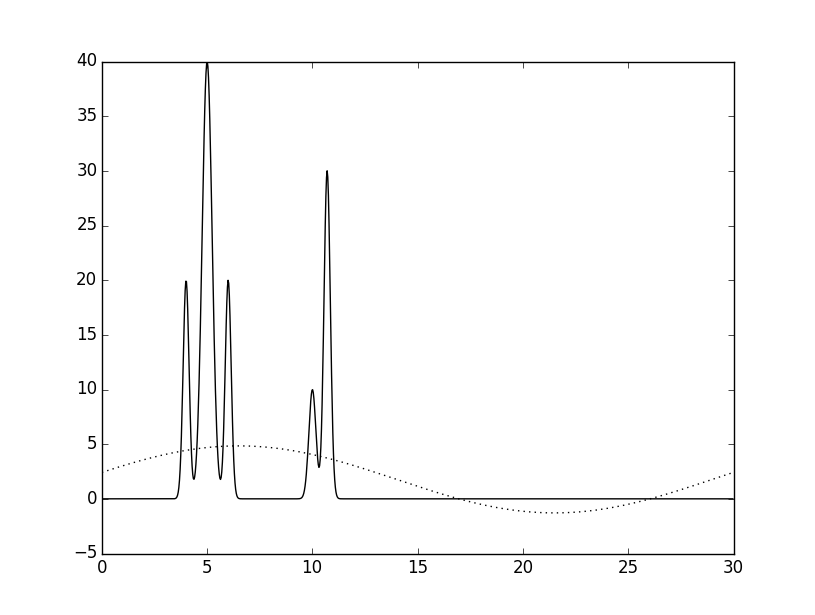
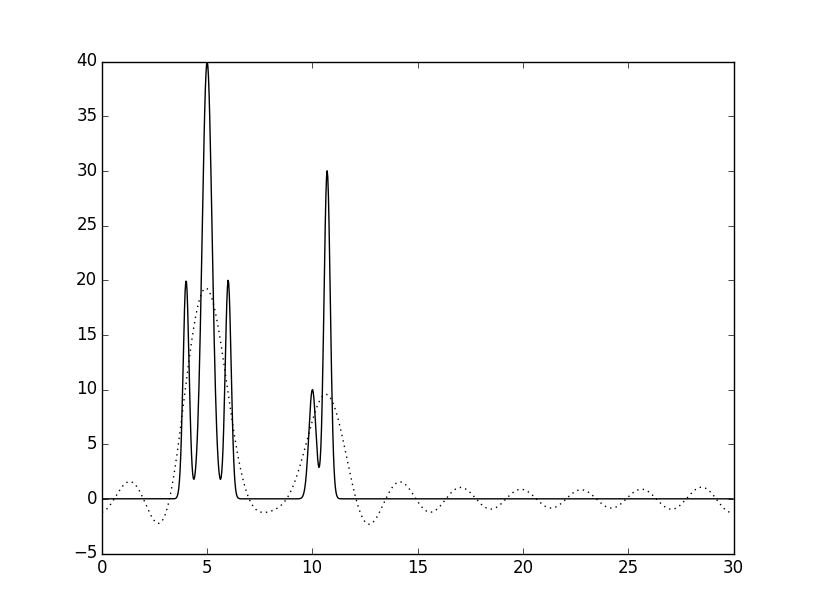
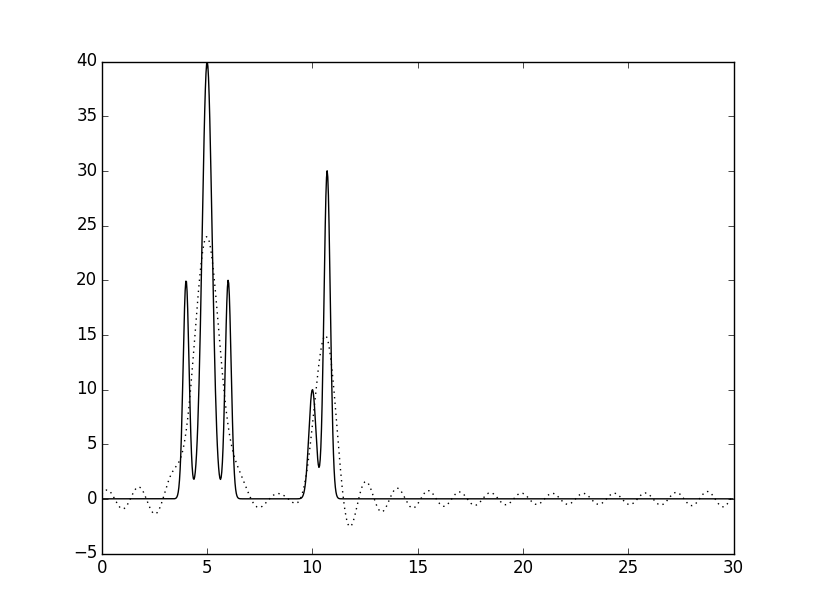
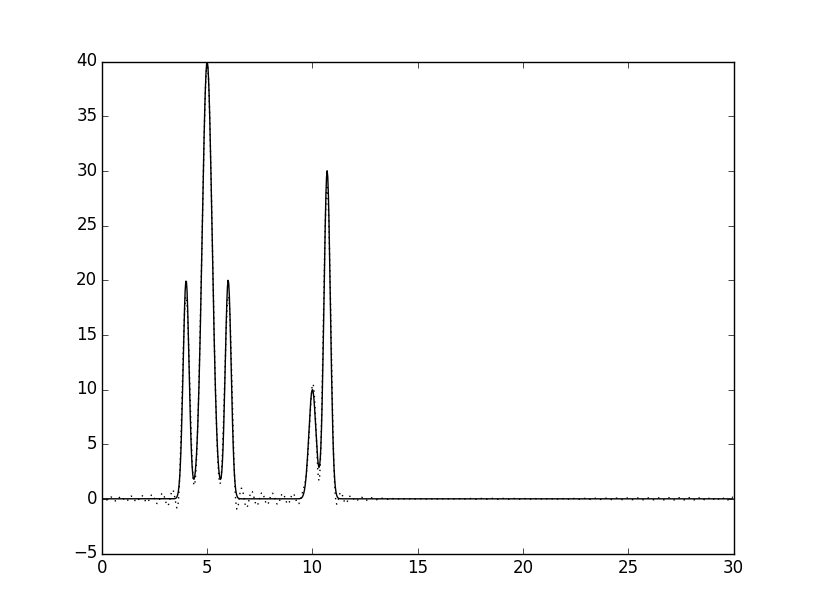
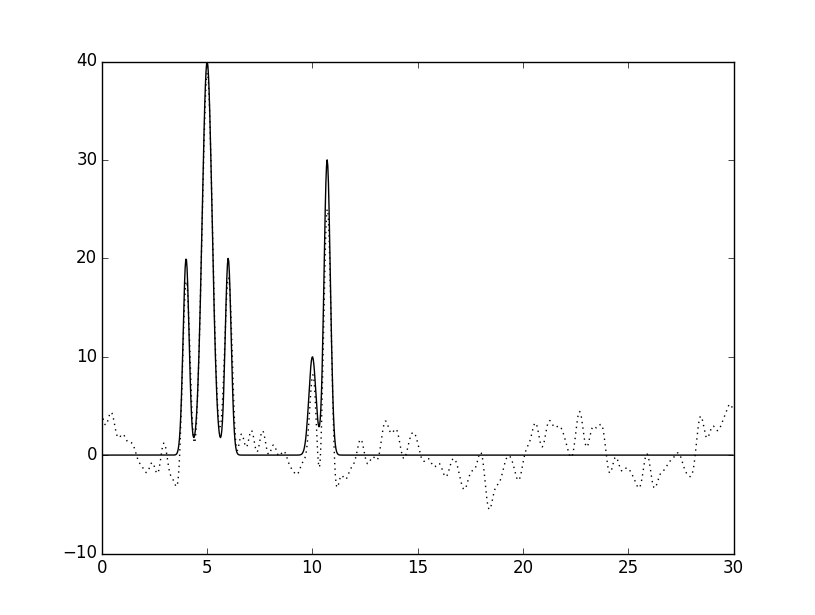
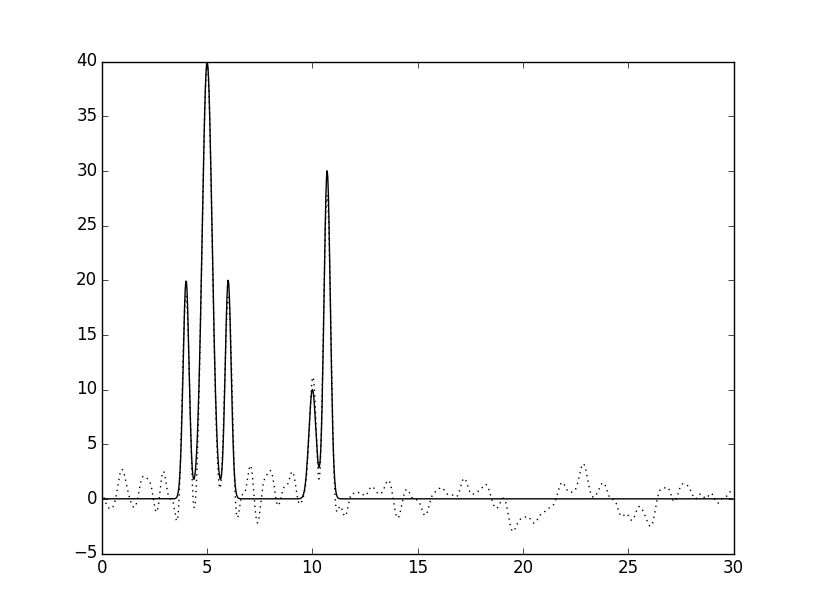
По частичным суммам ряда с помощью скрипта fourier2func восстанавливалась исходная функция распределения ЭП. Были взяты разные частичные суммы (разное число грамоник). Их наложение на исходную функцию показано на рисунке 2. 



 

  
  
  
 

 

  
1

  
10

  
20

 

 

  
  
  
 

 

  
40

  
60

  
80

 




Рисунок 2. Наложения восстановленных функций (пунктир) на исходную (сплошная линия), полученные скриптом fourier2func. Указаны количества гармоник от начала разложения использованные при восстановлении.


Видно, что с возрастанием числа использованных первых гармоник разложения точность восстановления увеличичвается и в конце концов графики почти полностью совпадают. 



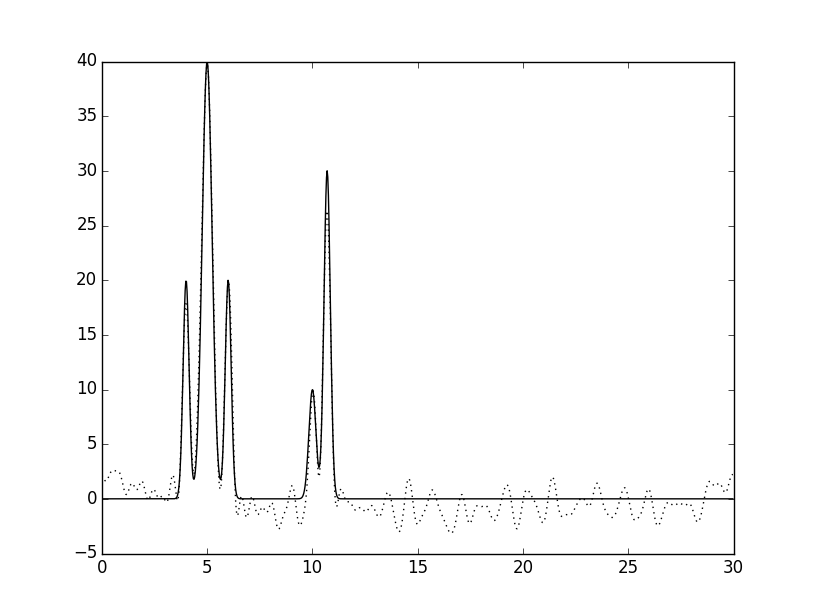
Скрипт func2fourier также позволяет добавлять шум в амплитуды (F) и фазы (P). На рисунке 3 показано восстановлениепо 60 гармоникам с разными парамтерами шума, видно, что он сильно мешает различать исходные молекулы.


 

  
  
  
 

 

  
P=20

  
F=20

  
F=10 P=10

 




Рисунок 3.Восстановление с добавлением шума.


Затем для восстановления использовались не первые n гармоник, а только некоторые из них (неполный набор), результат показан на рисунке 4.





 

  
  
  
 

 

  
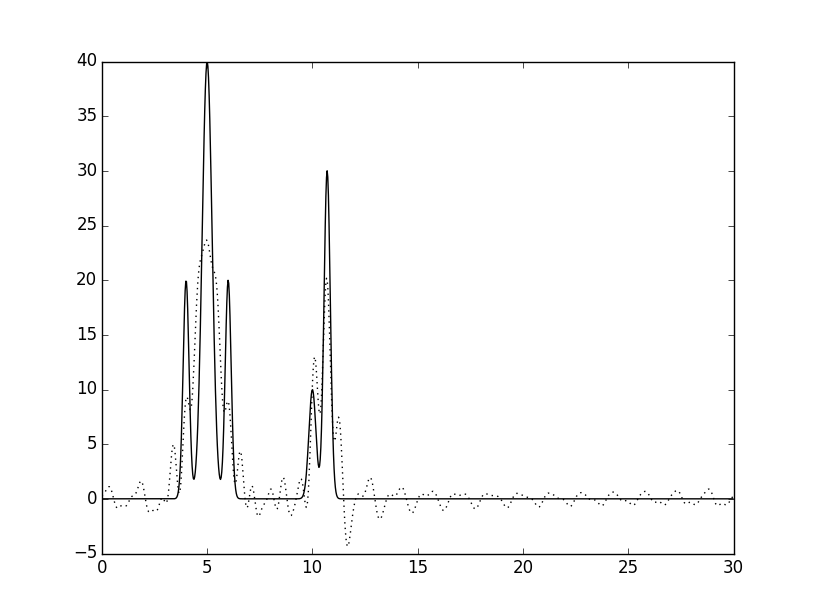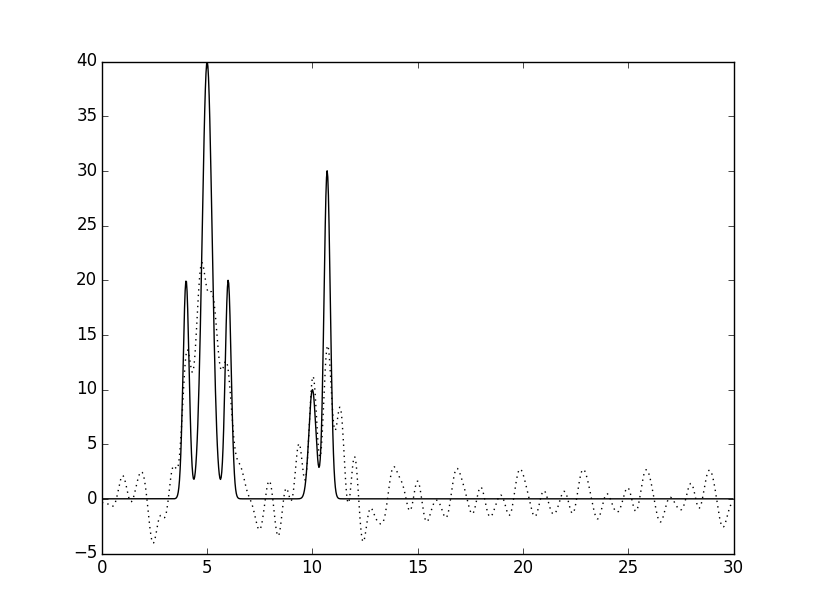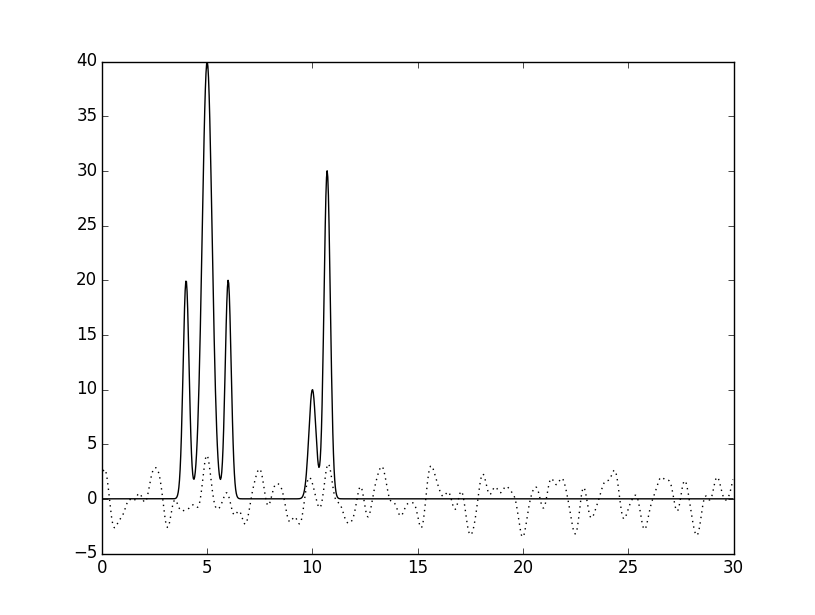0-20, 40-60

  
0-10, 20, 30, 40-50

  
11,25,37,42,57

 




Рисунок 4. Восстановлене по неполному набору гармоник.


Видно, что восстановление потеряло в качестве, как и ожидалось. Пики сместились, изменилась их высота, появились пики, которые можно принять за сиганл от атомов, а в последнем случае восстановленная функция целиком неотличима от шума.

Полученные результаты просуммированы в таблице.





 Набор гармоник
 Разрешение ( Å)
 Полнота данных (%)
 Шум амплитуды (%)
 Шум фазы (%)
 Качество восстановления
 Комментарии




 
Полный набор гармоник





 0-1
 30
 100
 0
 0
 Плохое
 




 0-10
 3
 100
 0
 0
 Среднее
 




 0-20
 1,5
 100
 0
 0
 Хорошоее
 




 0-40
 0,75
 100
 0
 0
 Отличное
 




 0-60
 0,37
 100
 0
 0
 Отличное
 




 0-60
 0,37
 100
 20
 0
 Отличное
 




 0-60
 0,37
 100
 0
 20
 Отличное
 




 0-60
 0,37
 100
 10
 10
 Отличное
 




 
Неполный набор гармоник





 0-20, 40-60
 0,37
 67
 0
 0
 Хорошее
 




 0-10, 20, 30, 40-50
 0,6
 37
 0
 0
 Среднее
 




 11, 25, 37, 42, 57
 0,7
 8
 0
 0
 Плохое
 






Из таблицы видно, что чем больше использовано гармоник при восстановлении функции ЭП, тем лучше качество восстановления. При хорошем восставновлении шум не мешает различить сигнал от атомов. 
Полный набор гармоник лучше восстанавливает функцию, чем неполный.

Видно также, что типичные значения разрешения для рентгеноструктурного анализа не соотвествуют лучшему качеству восстановления. 
 

  

   

    Главная страница
    Первый семестр
    Второй семестр
    Третий семестр
    Обо мне
    Ссылки
   

  



 

 © Марк Меерсон, 2015

Последнее обновление 27.10.2015