Занятие 6.
Изучение работы методов контроля температуры в GROMACS.
Суть задания состоит в изучении реализации контроля температуры в молекулярной динамике на примере GROMACS. Объект исследования это одна молекула этана.
-
Начнем с того, что подготовим файл координат и файл топологии. С прошлого занятия возьмем gro файл с 38 молекулами этана. Создадим индекс файл, в котором будет группа из одной молекулы этана:
make_ndx -f box_38.gro -o 1.ndx
После запуска команды появится приглашение к вводу. Сначала ознакомимся с программой - нажав "h" + enter. Выберем остаток номер 1. Нажмем enter и увидим, что появилась новая группа.
Теперь создадим gro файл с одной молекулой и зададим ячейку . При запуске ediconf выберем номер соответствующей группы из одной молекулы.editconf -f box_38.gro -o et1.gro -n 1.ndx #зададим ячейку и расположим молекулу по центру ячейку editconf -f et1.gro -o et.gro -d 2 -c
Необходимо исправить файл топологии et.top из прошлого задания. Нужно в разделе [ molecules ] изменим количество молекул этана (исправим 38 на 1). -
Даны 5 файлов с разными параметрами контроля температуры:
be.mdp - метод Берендсена для контроля температуры.
vr.mdp - метод "Velocity rescale" для контроля температуры.
nh.mdp - метод Нуза-Хувера для контроля температуры.
an.mdp - метод Андерсена для контроля температуры.
sd.mdp - метод стохастической молекулярной динамики.
- Сначала построим входные файлы для молекулярно-динамического движка mdrun с помощью grompp:
grompp -f ${i}.mdp -c et.gro -p et1.top -o et_${i}.tpr # где i: be,vr,nh,an,sd список mdp файлов - Для каждого из полученных 5 tpr файлов запускаем mdrun:
mdrun -deffnm et_${i} -v -nt 1 -
Теперь можно перейти к анализу результатов. Для визуального анализа проведем для каждой из 5 систем конвертацию в pdb:
trjconv -f et_${i}.trr -s et_${i}.tpr -o et_${i}.pdbНаблюдения:
Метод Берендсена Сначала молекулы слегка колеблются и вращаются, а потом амплитуда колебаний уменьшается и молекулы начинают быстро вращаться. (Посмотреть ролик.)
Метод Андерсена Наблюдаются колебания только по длинам связей и углам, вращения нет, поэтому скорее всего эта модель хорошо отражает систему, в которой этан прочно связан (в кристалле). (Посмотреть ролик.)
Метод Нуза-Хувера Происходят различные вращения, причем в различных конформациях, а также небольшие колебания по связям, поэтому метод похож на реальное поведение молекулы.(Посмотреть ролик.)
Метод стохастической молекулярной динамики описывает случайное перемещение молекулы в пространстве, плохо видно вращение и колебание связей молекулы. (Посмотреть ролик.)
Метод "Velocity rescale" Данный метод похож на метод Нуза-Хувера, но уменьшено вращение и увеличена амплитуда. (Посмотреть ролик.) - Сравним потенциальную энергию связи и кинетическую энергию для каждой из 5 систем:
g_energy -f et_${i}.edr -o et_${i}_en.xvg
Построим графики изменения энергий. Воспользуемся Gnuplot:
set datafile commentschars "#@&" plot "./et_be_en.xvg" using 1:2, "./et_be_en.xvg" using 1:3 .... plot "./et_sd_en.xvg" using 1:2, "./et_sd_en.xvg" using 1:3
Полученные в результате графики для разных методов представлены ниже:
метод Берендсена: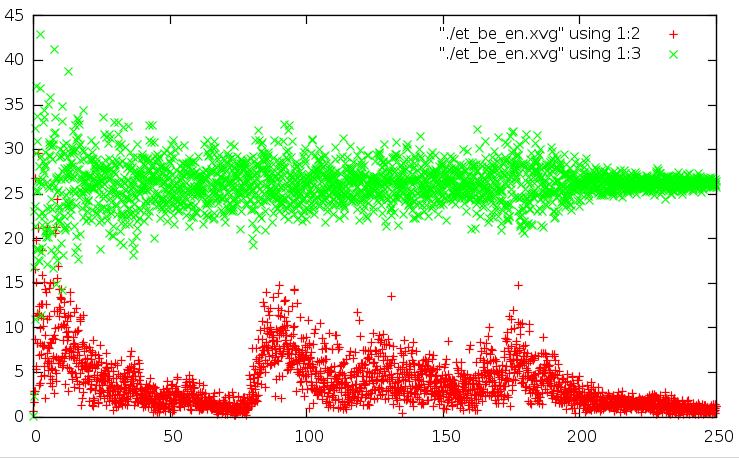
метод "Velocity rescale":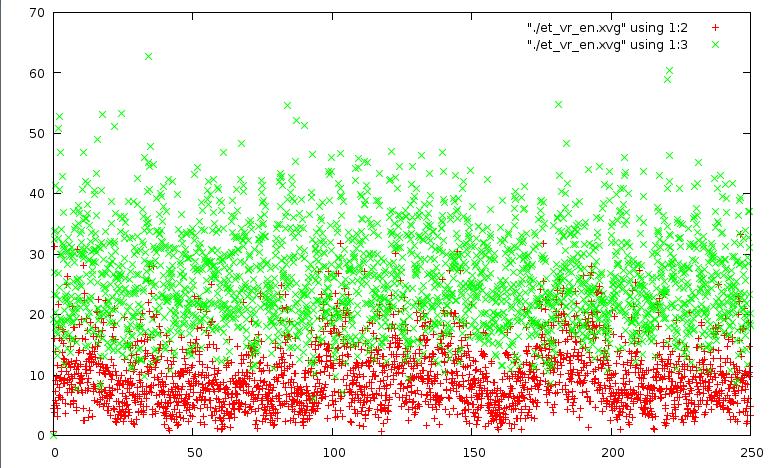
метод Нуза-Хувера: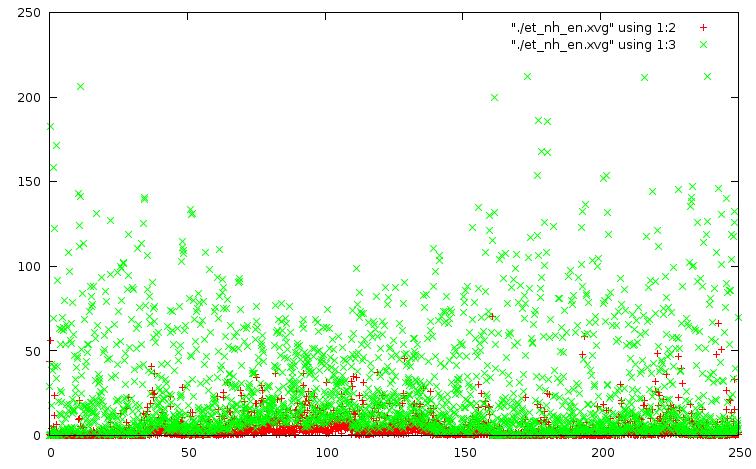
метод Андерсена: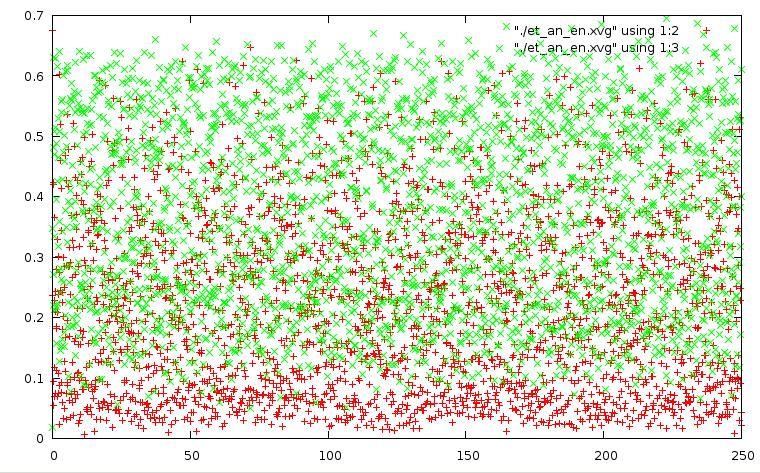
метод стохастической молекулярной динамики: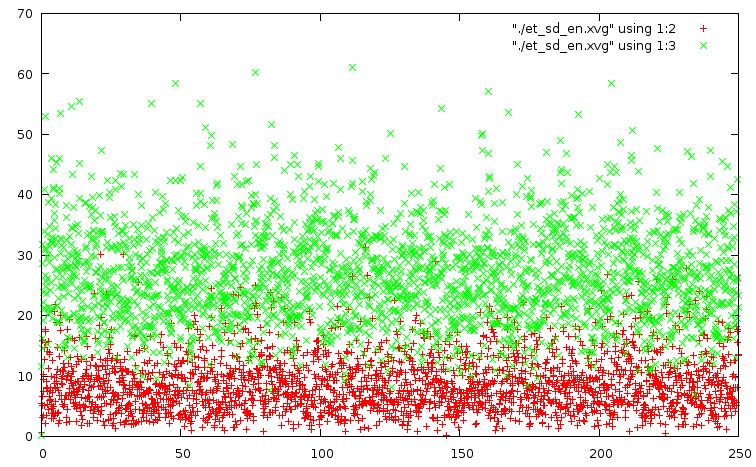
-
Рассмотрим распределение длины связи C-C за время моделирования. Сначала создадим индекс файл b.ndx с одной связью:
[ b ] 1 2
Запустим утилиту по анализу связей g_bond:g_bond -f et_${i}.trr -s et_${i}.tpr -o bond_${i}.xvg -n b.ndxПостроим графики распределения длин связей, используя boxes в Gnuplot:
plot "./bond_be.xvg" with boxes .... plot "./bond_sd.xvg" with boxes
Полученные в результате графики для разных методов представлены ниже:
метод Берендсена: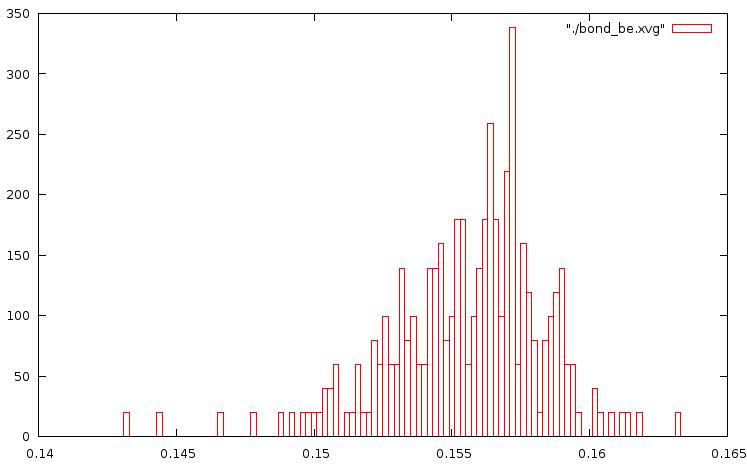
метод "Velocity rescale":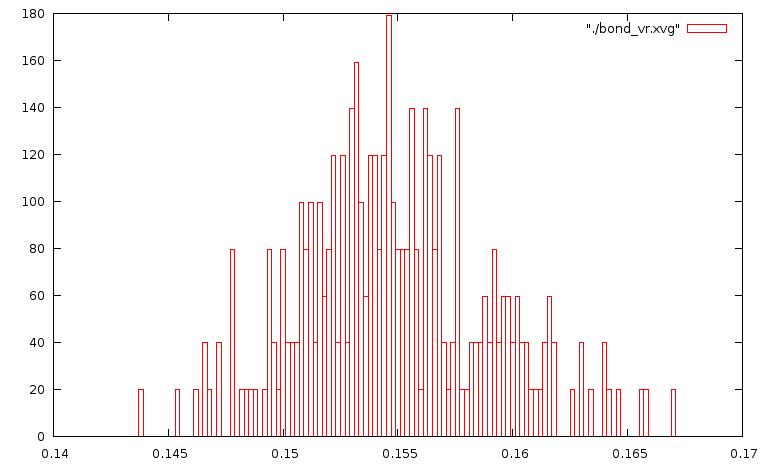
метод Нуза-Хувера: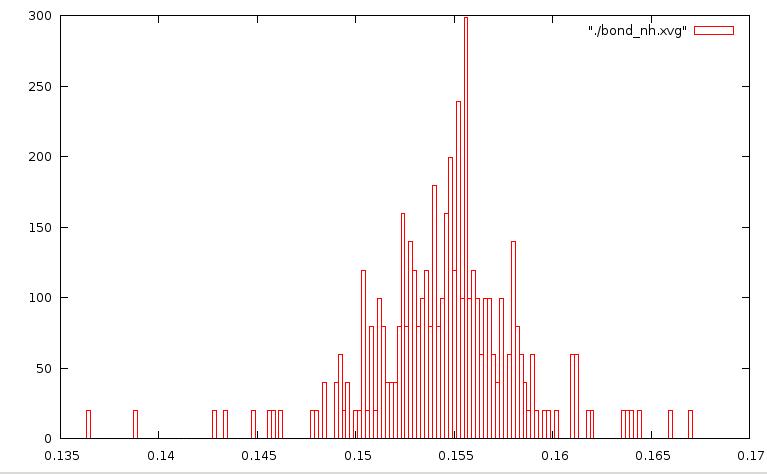
метод Андерсена: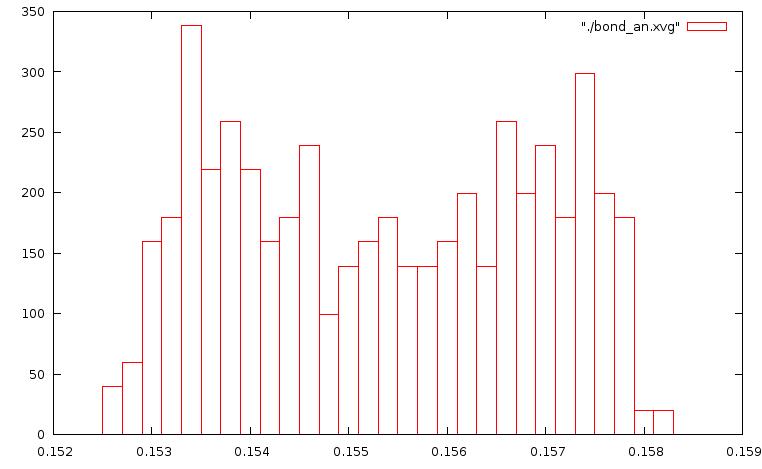
метод стохастической молекулярной динамики: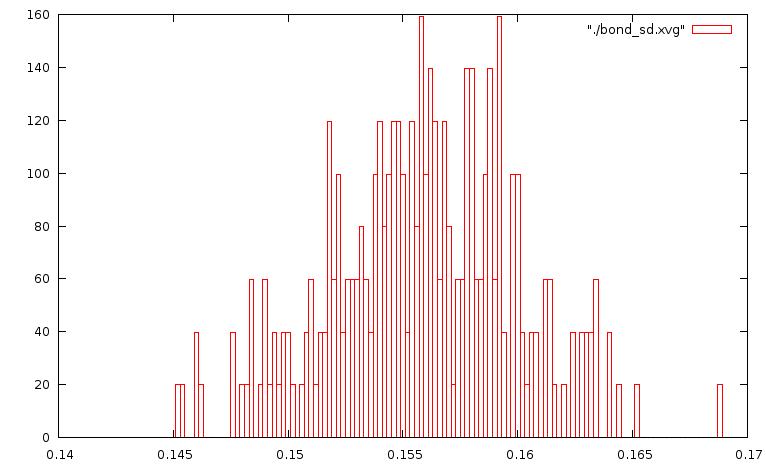
-
Сравним полученные наблюдения с распределением Максвелла-Больцмана:
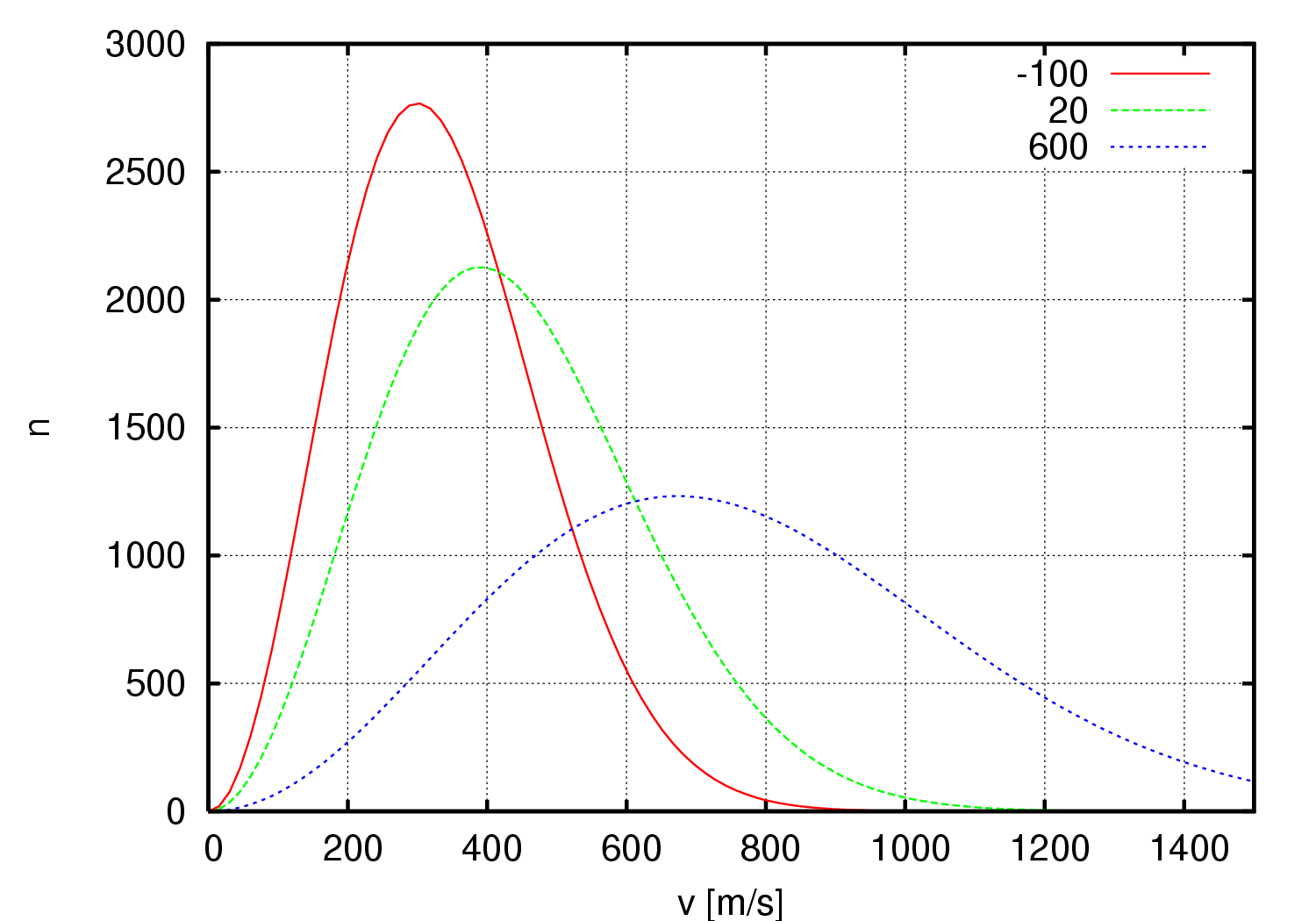
Данное распределение похоже на графики методов Нуза-Хувера, "Velocity rescale" и стохастической молекулярной динамики. Исходя не только из распределения и роликов данных сиситем, можно сказать, что наиболее реалистичны методы Нуза-Хувера и "Velocity rescale".
<<Обратно на шестой семестр
<<Обратно на главную страницу©Лелекова Мария,2011