Алгоритмы реконструкции деревьев. Укоренение и бутстреп.
Укоренение в среднюю точку
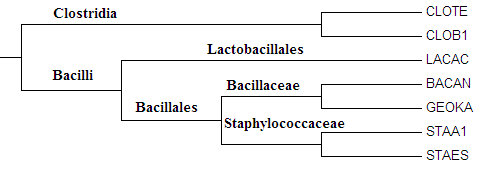
Изображение 1 Правильное дерево.
А теперь укореним в среднюю точку деревьево, построенное с помощью метода Neighbour joining tree using blosum62. Для того, чтобы укоренить это дерево в среднюю точку, использовалась программа retree пакета Phylip. Укоринением в среднюю точку, мы принимаем гипотезу о молекулярных часах, для построения графа с различной длиной ветвей. На Изображении 2 показано дерево укорененое retree.
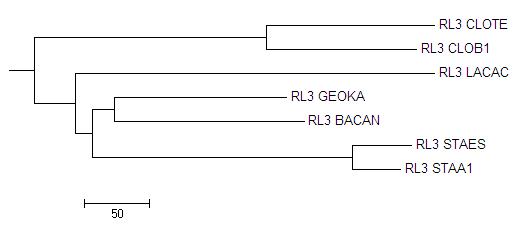
Изображение 2 Дерево построенное алгоритмом Neighbour joining tree using blosum62 и переукорененное в среднюю точку программой retree.
Как видно, дерево было переукоренено правильно.
Укоренение с использованием внешней группы
Метод максимальной экономии "Maximum parsimony" предполагает работу с выравниванием последовательностей и не учитывает длину ветвей. А значит дерево построенное таким методом, нельзя укоренить в среднюю точку. Для решения такой задачи следует использовать укоренение с помощью внешней группы. Мы используем теже последовательности что и раньше, но + прибавляем к ним белок того же семейства из кишечной палочки (Escherichia coli, ECOLI), как внешнюю группу. Строим выравнивание програмой muscle. Выравнивение даем на вход программе MEGA и используем метод максимальной экономии. На Изображении 3 и Изображении 4 представлены результаты работы.
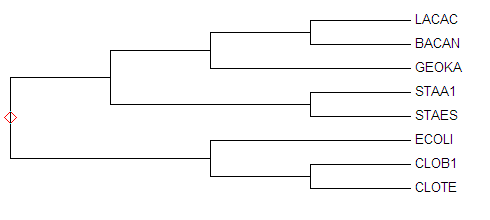
Изображение 3 Филогенетическое дерево построеное с помощью метода максимальной экономии(Maximum parsimony) и укорененое спмощью внешней группы ECOLI.(укоренение обозначено красным ромбом)
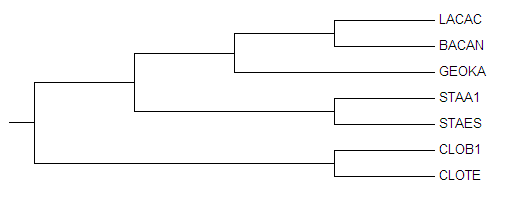
Изображение 2 Филогенетическое дерево построеное методом максимальной экономии(Maximum parsimony) без внешней групой ECOLI, но имеющее укореннение согласно предыдущему.
Нетрудно заметить, что дерево получилось правильным
Бутстрэп
В этом блоке был проведён бутстреп-анализ (количество реплик взято равным 100) при построении филогенетического дерева методом "Maximum parsimony".
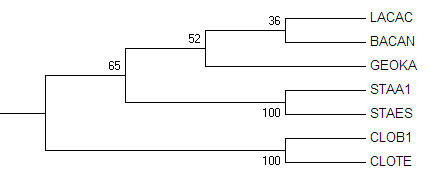
Изображение 3 Филогенетическое дерево построеное методом максимальной экономии(Maximum parsimony) являющееся исходным("Original tree").
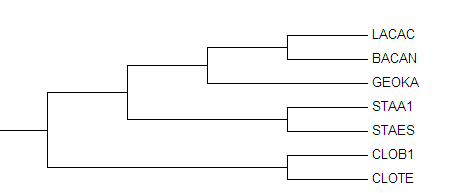
Изображение 4 Филогенетическое дерево построеное методом максимальной экономии(Maximum parsimony) оптимальное с точки зрения алгоритма бутстреп("Bootstrap consensus tree").
Как видно оба дерева поностью совпадают с исходным и построены правильно.