Восстановление электронной плотности
Задание функции.
На отрезке [0,30] (Å) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 Å друг от друга. Молекулы расположены на расстоянии 3-5 Å (водородная связь или гидрофобное взаимодействие между ними). Всего 5-7 атомов (2+3 или 2+3+2; возможны другие варианты). Электронные плотности (ЭП) атомов описываются гауссовой кривой. Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py:
python compile-func.py -g 10,3,2+40,3,4.7+17,3,5+24,2,9.9+33,3,12.1
В результате получаем выходной файл скрипта с парами (Х,У) и график функции:
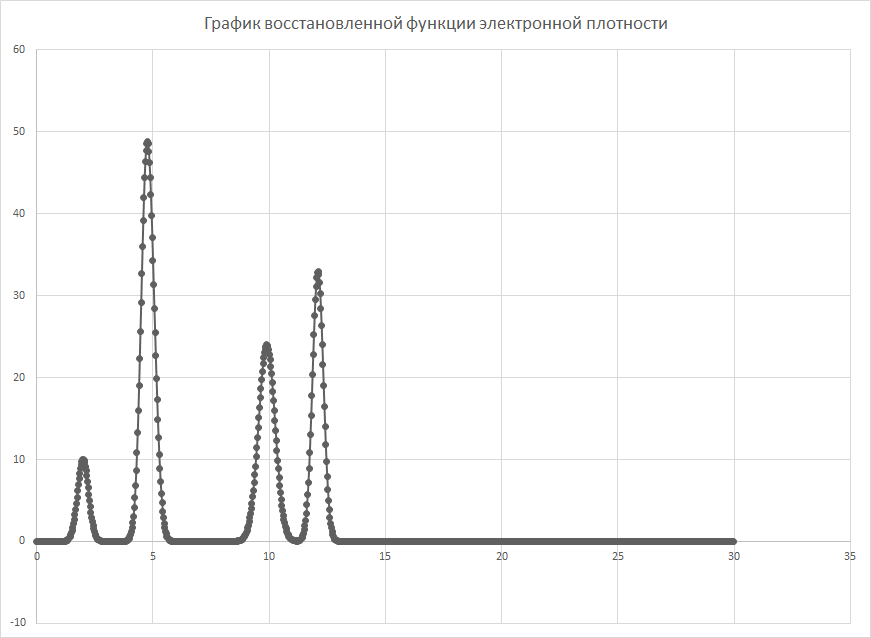
Рисунок 1График восстановленной функции электронной плотности
Количество гармоник для составления этой функции было взято равным 499. И как мы видим, получается отличное восстановление функции электорной плотности, т.е. по графику восстановленной функции можно определить положение максимумов всех гауссовых слагаемых.
Вос с помощью уже знакомого скрипта fourier2func.py и fourier-filter.py, который производит отбор гармоник, был произведен поиск минимального числа гармоник
Полный набор гармоник
С помощью уже скрипта fourier2func.py и fourier-filter.py, который производит отбор гармоник, был произведен поиск минимального числа гармоник, при котором наблюдается хорошее восстановление функции:
while read line;
python fourier-filter.py -r 0-${line} -i func_ft.txt -o func_ft_0-${line}.txt;
python fourier2func.py -f func.txt -i func_ft_0-${line}.txt -o two_func_0-${line}.txt -s True;
do mv 13.pdf ./${line}_s.pdf; done < list.txt
#файл list.txt содержит число гармоник
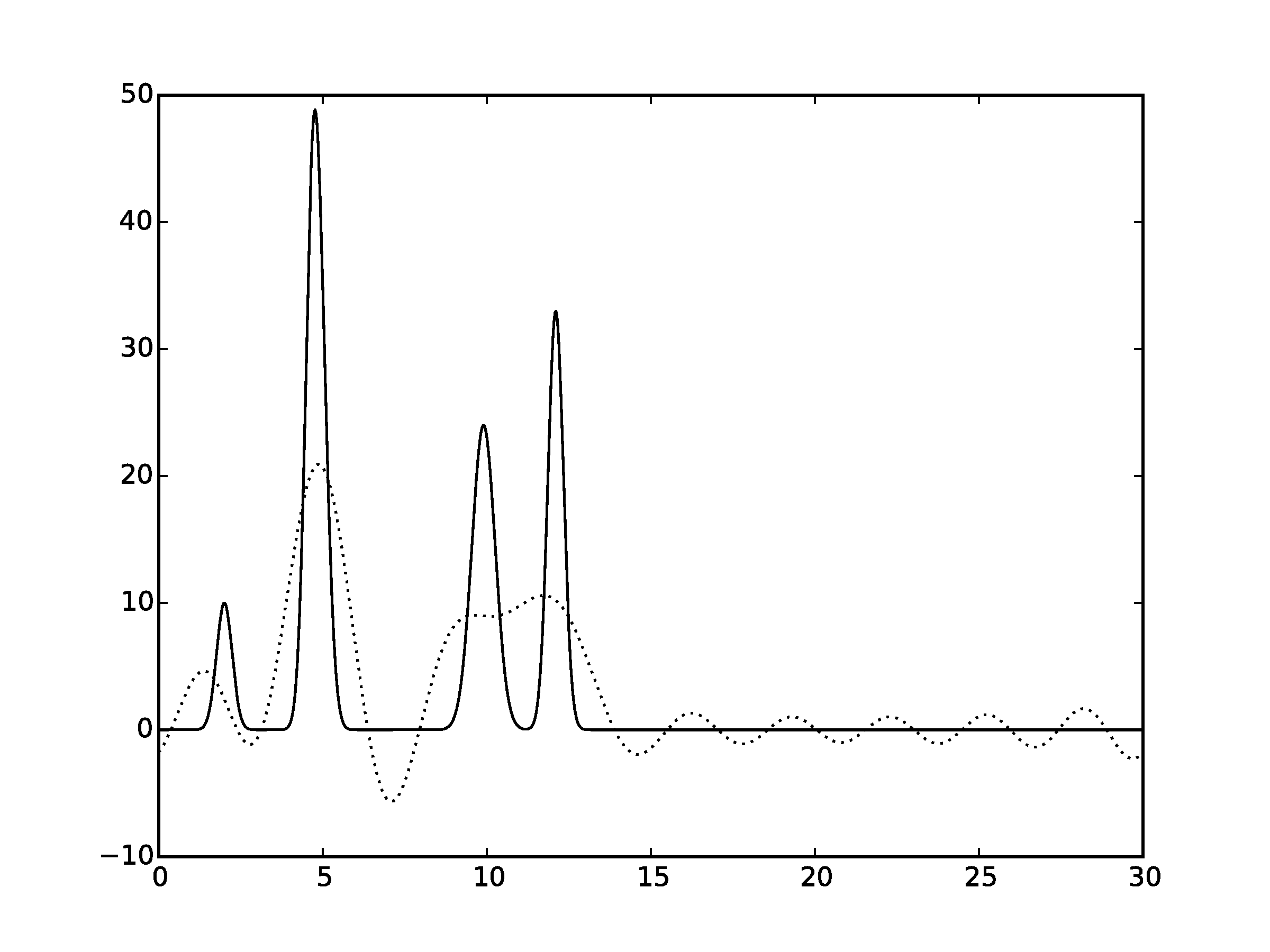
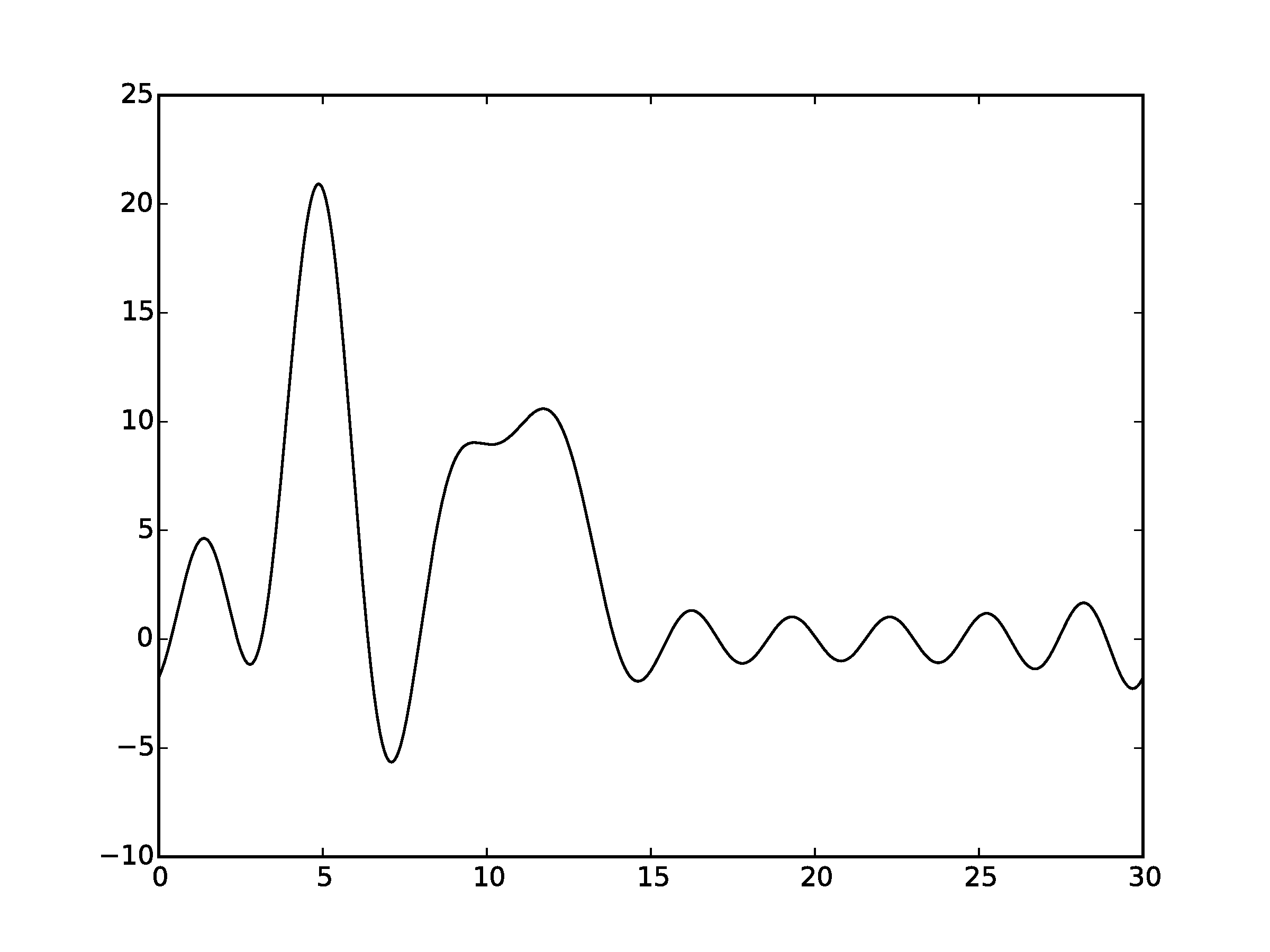
Рисунок 2.1Графики восстановленных функций, представленные пунктирной линией, для 10 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
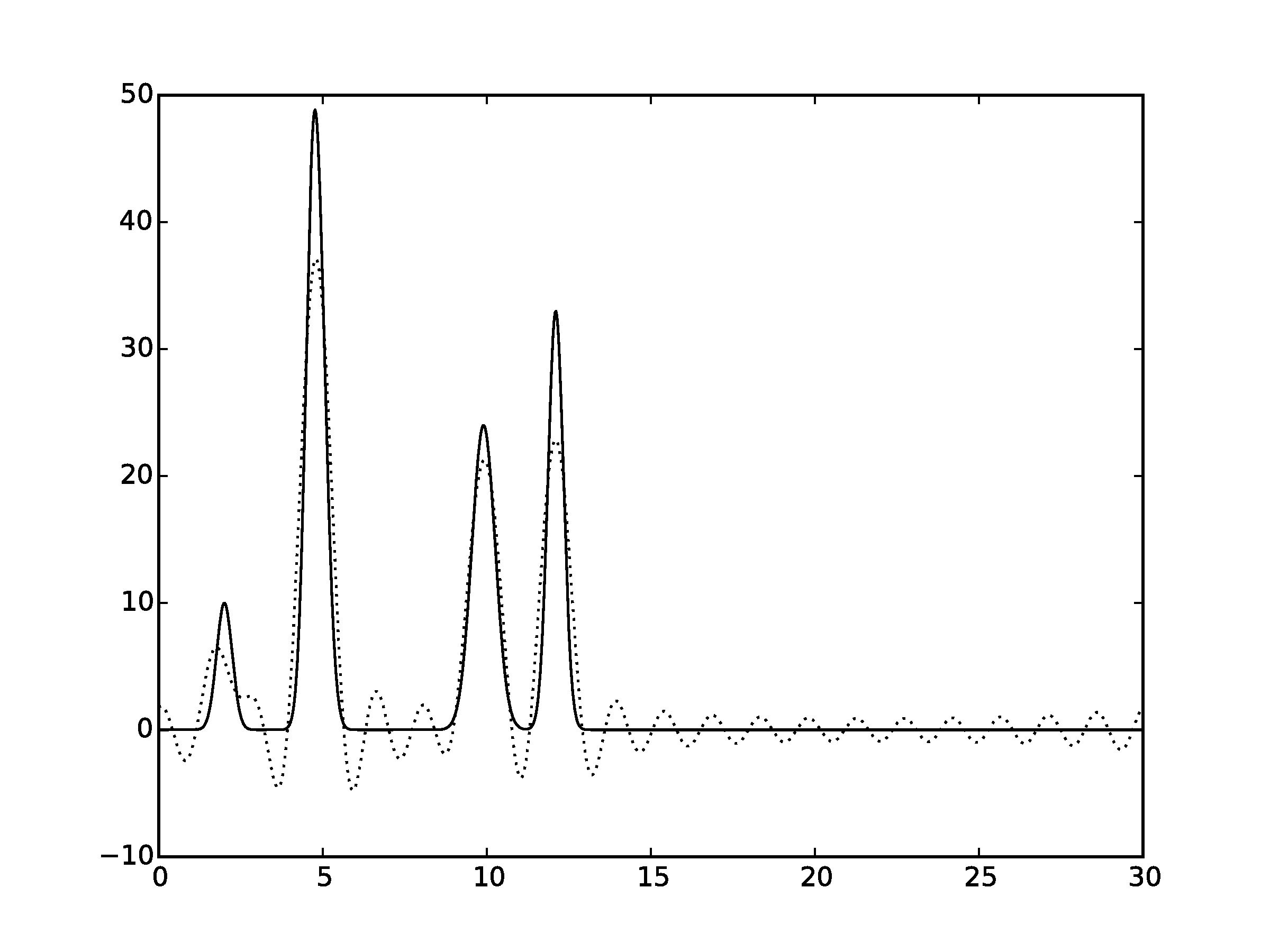
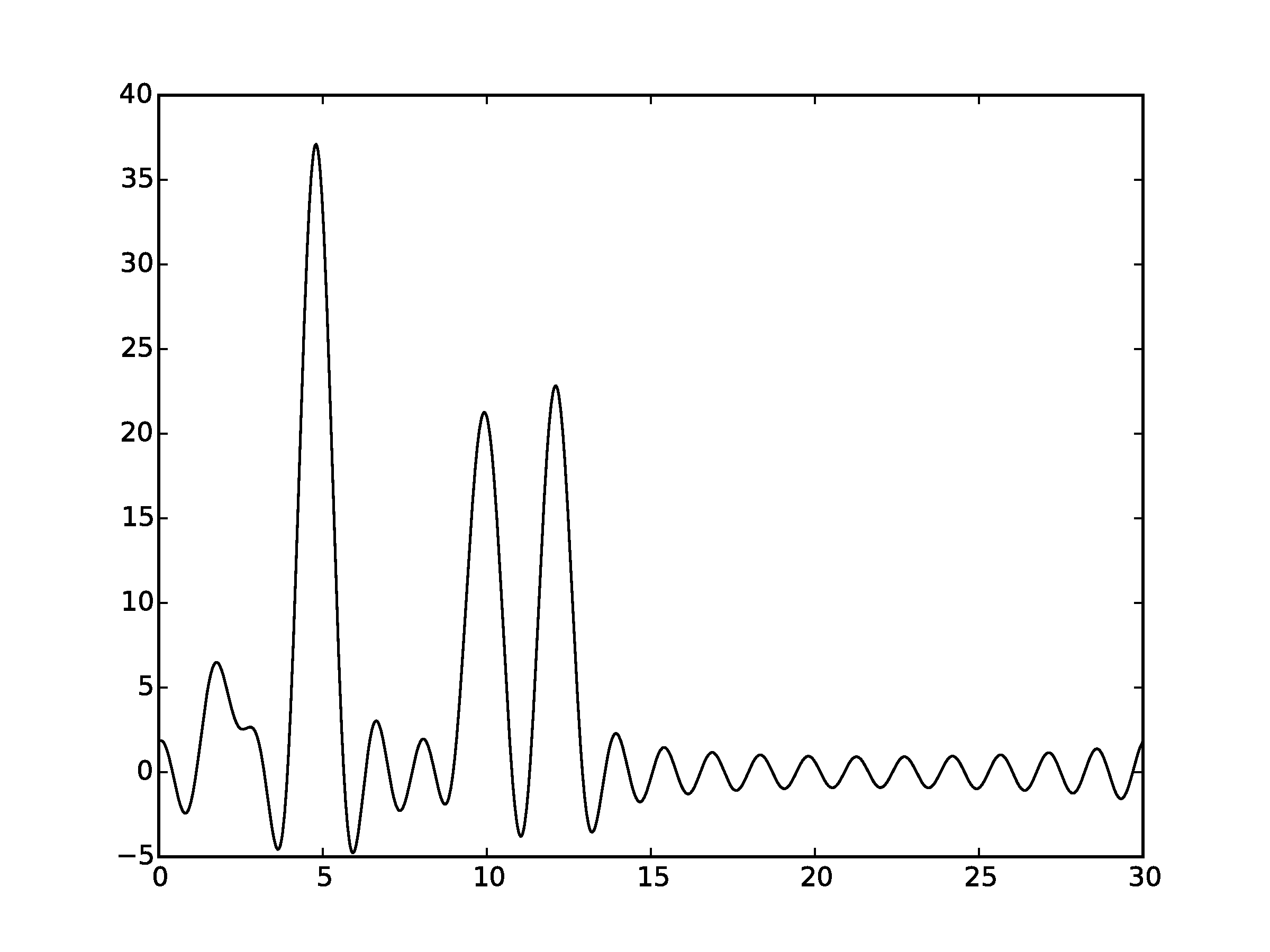
Рисунок 2.2Графики восстановленных функций, представленные пунктирной линией, для 20 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)

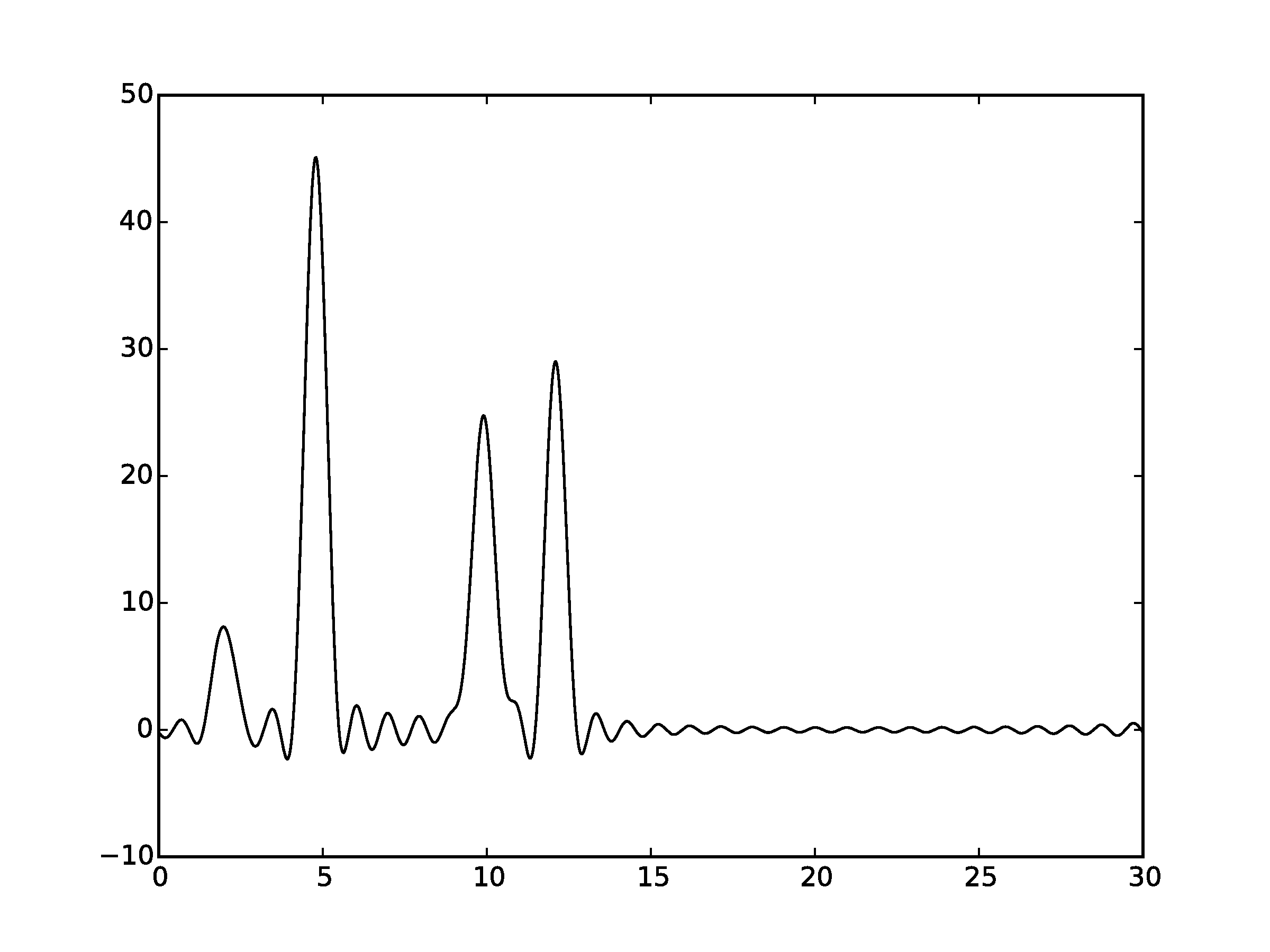
Рисунок 2.3Графики восстановленных функций, представленные пунктирной линией, для 30 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
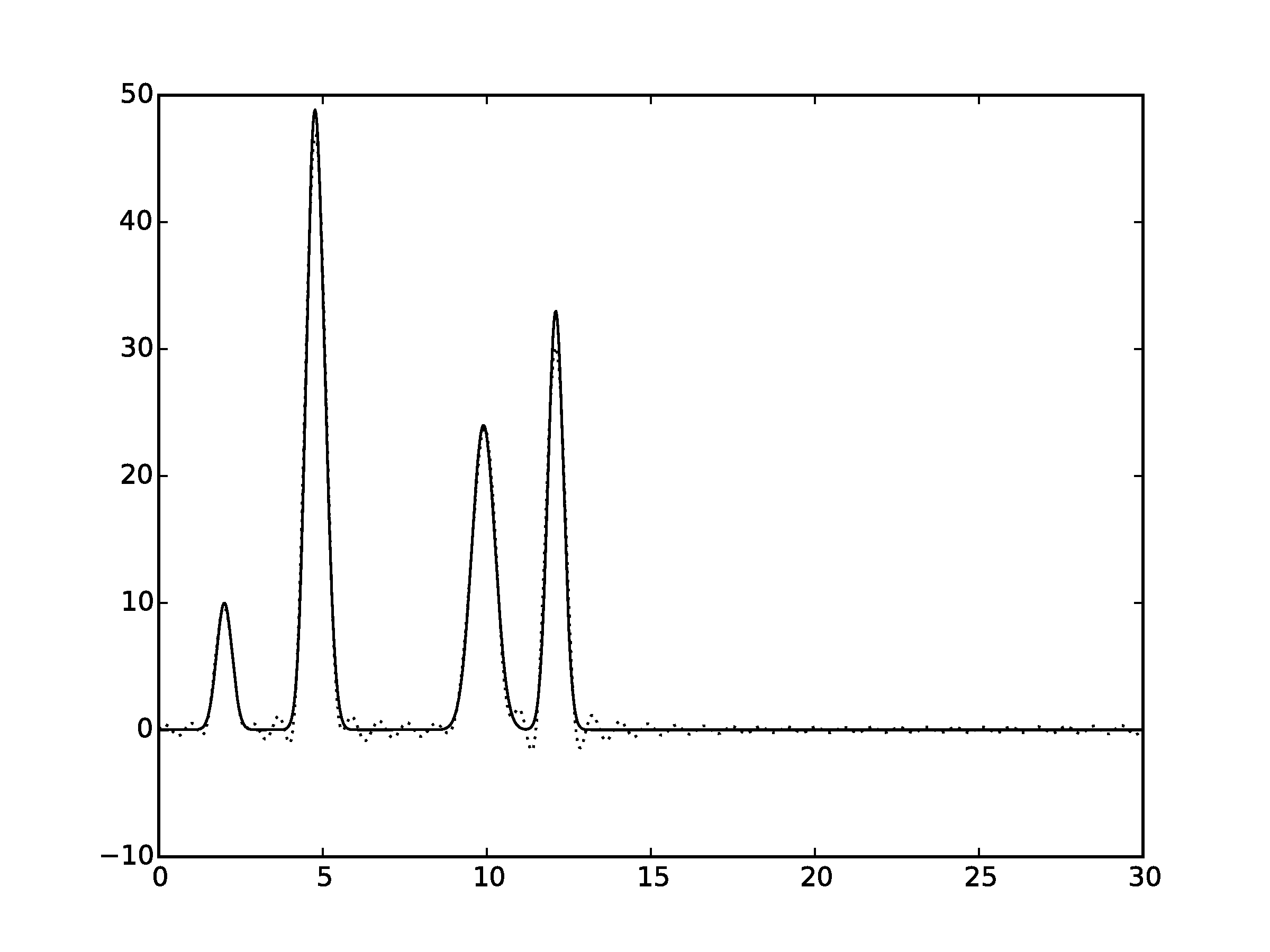
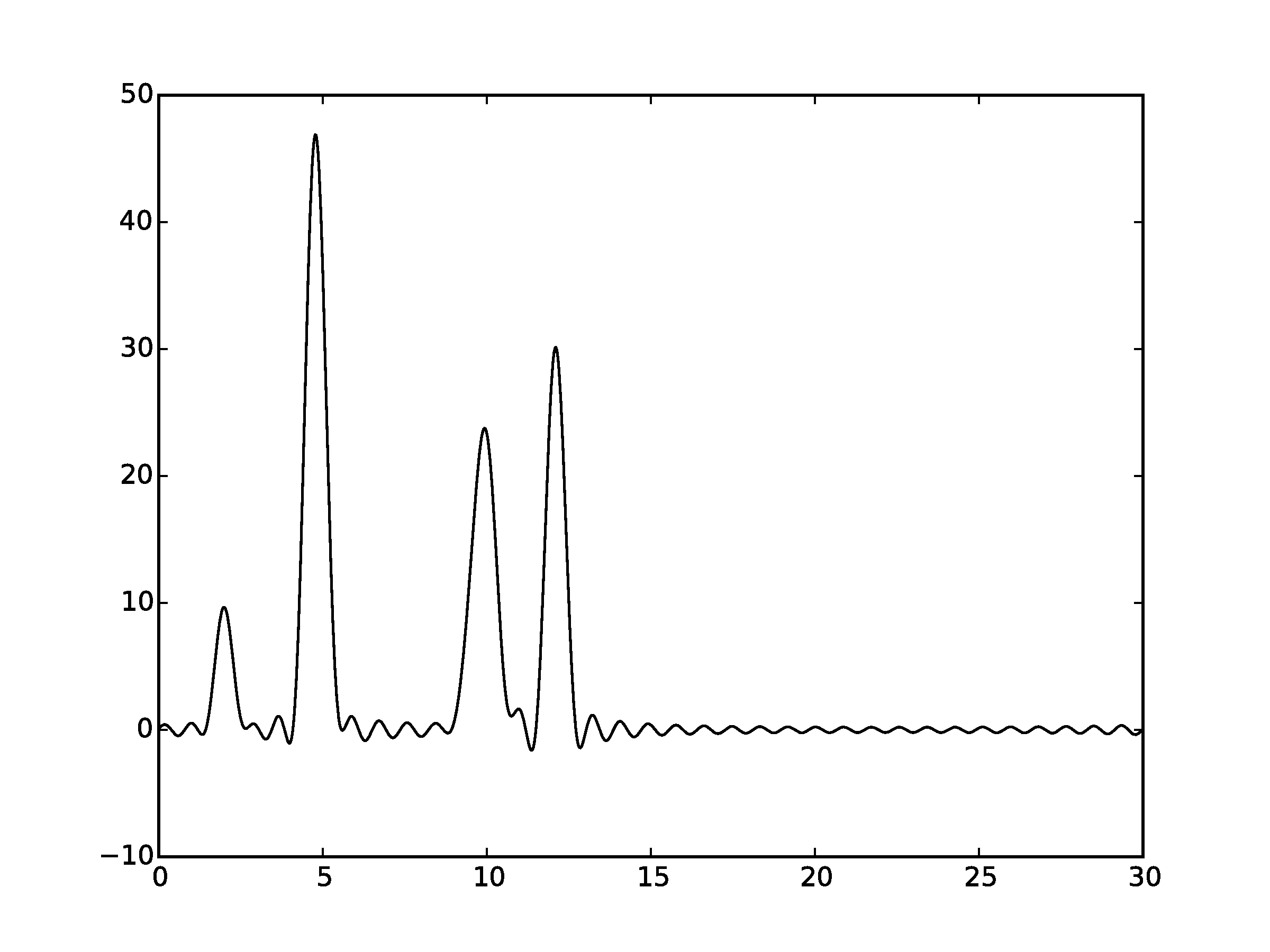
Рисунок 2.4Графики восстановленных функций, представленные пунктирной линией, для 35 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
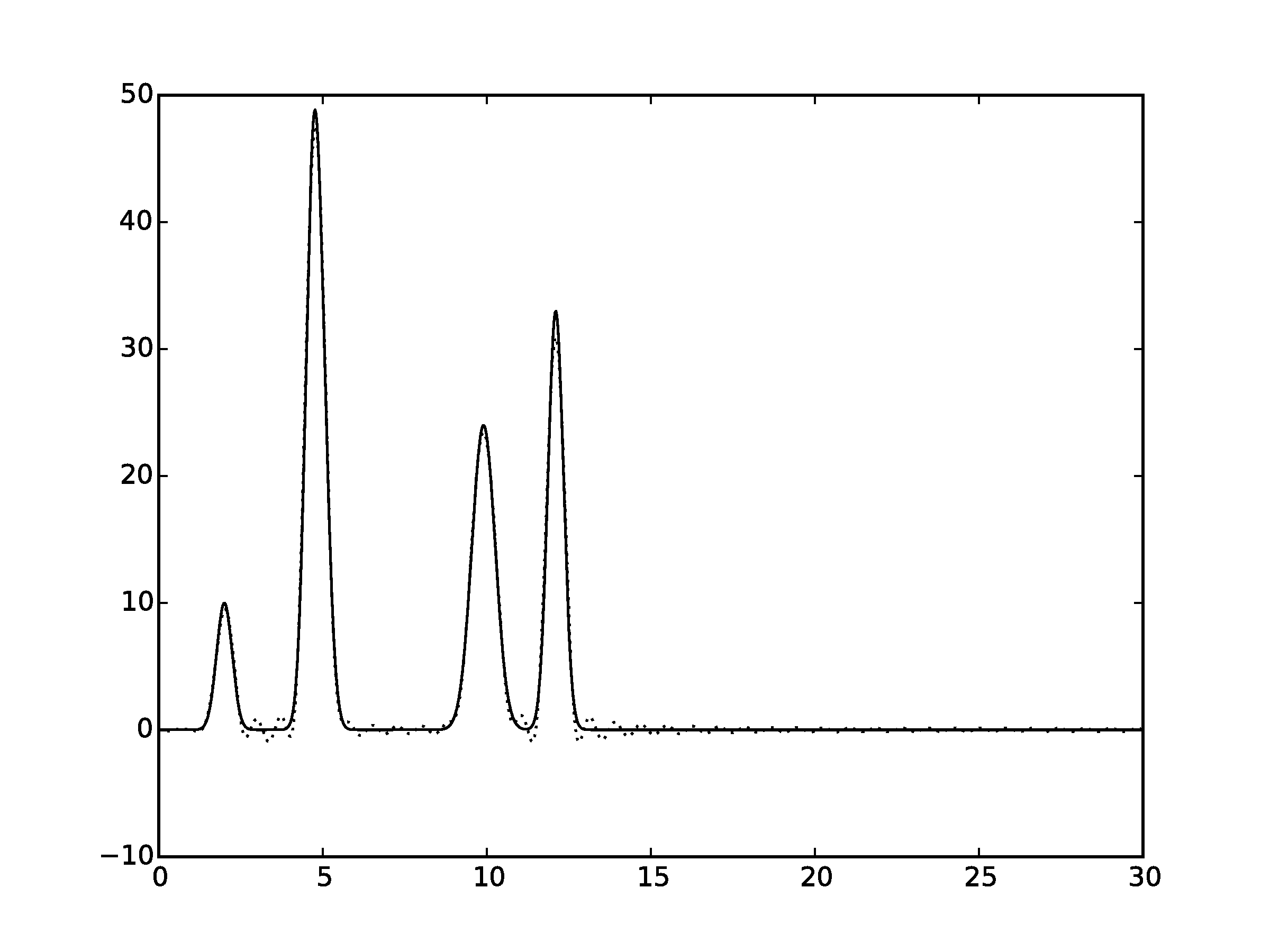

Рисунок 2.5Графики восстановленных функций, представленные пунктирной линией, для 37 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
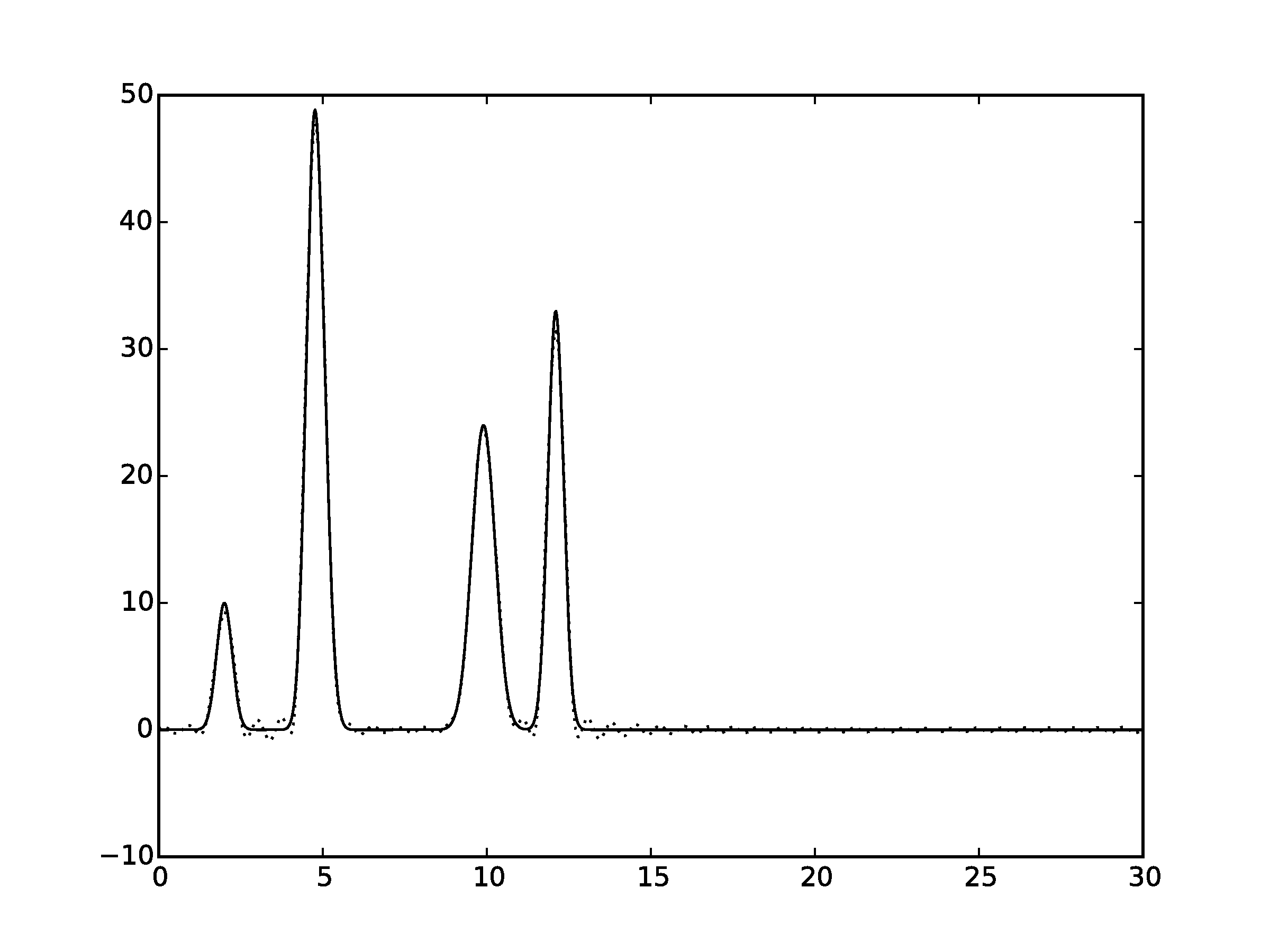
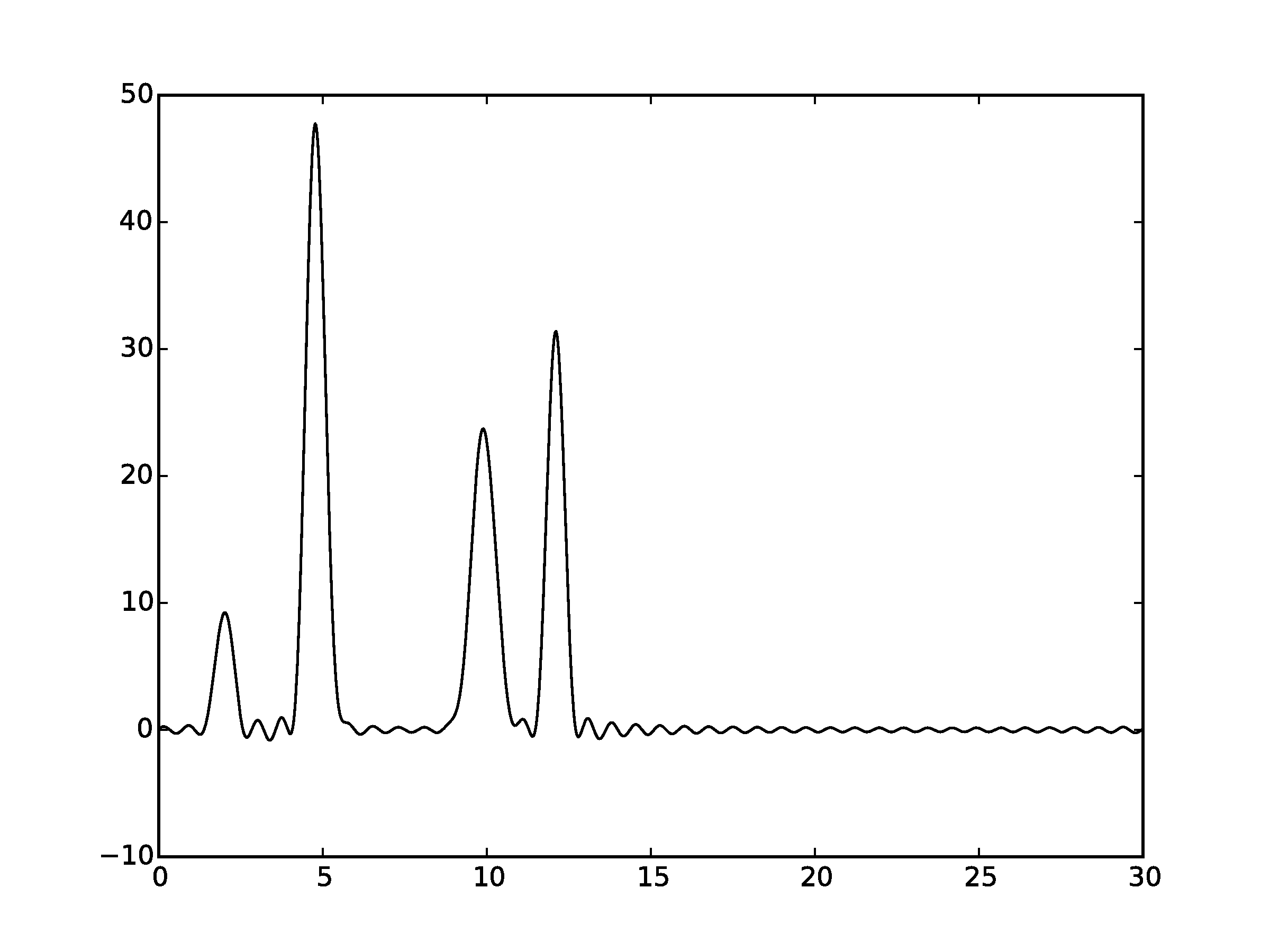
Рисунок 2.6Графики восстановленных функций, представленные пунктирной линией, для 40 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
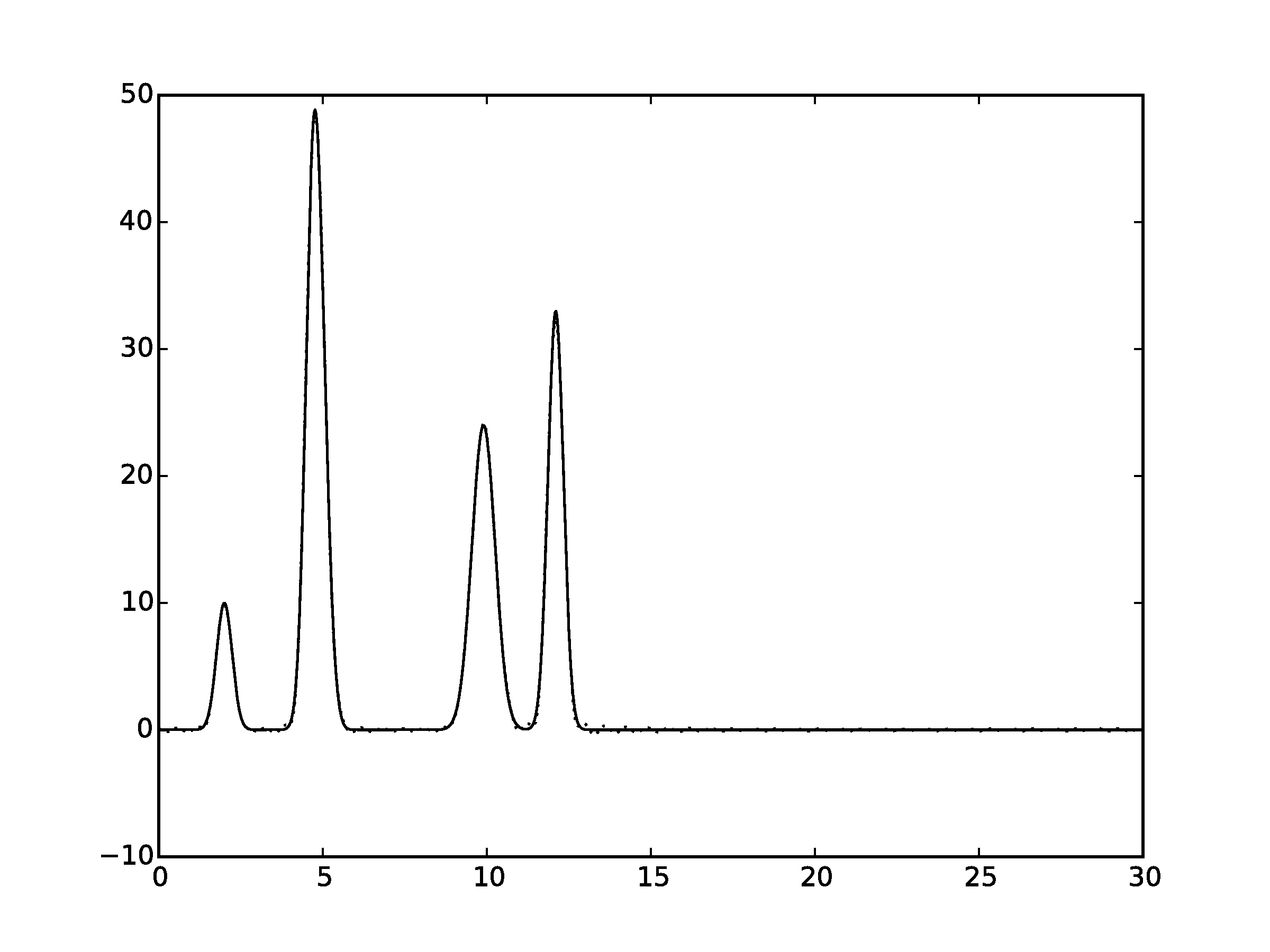
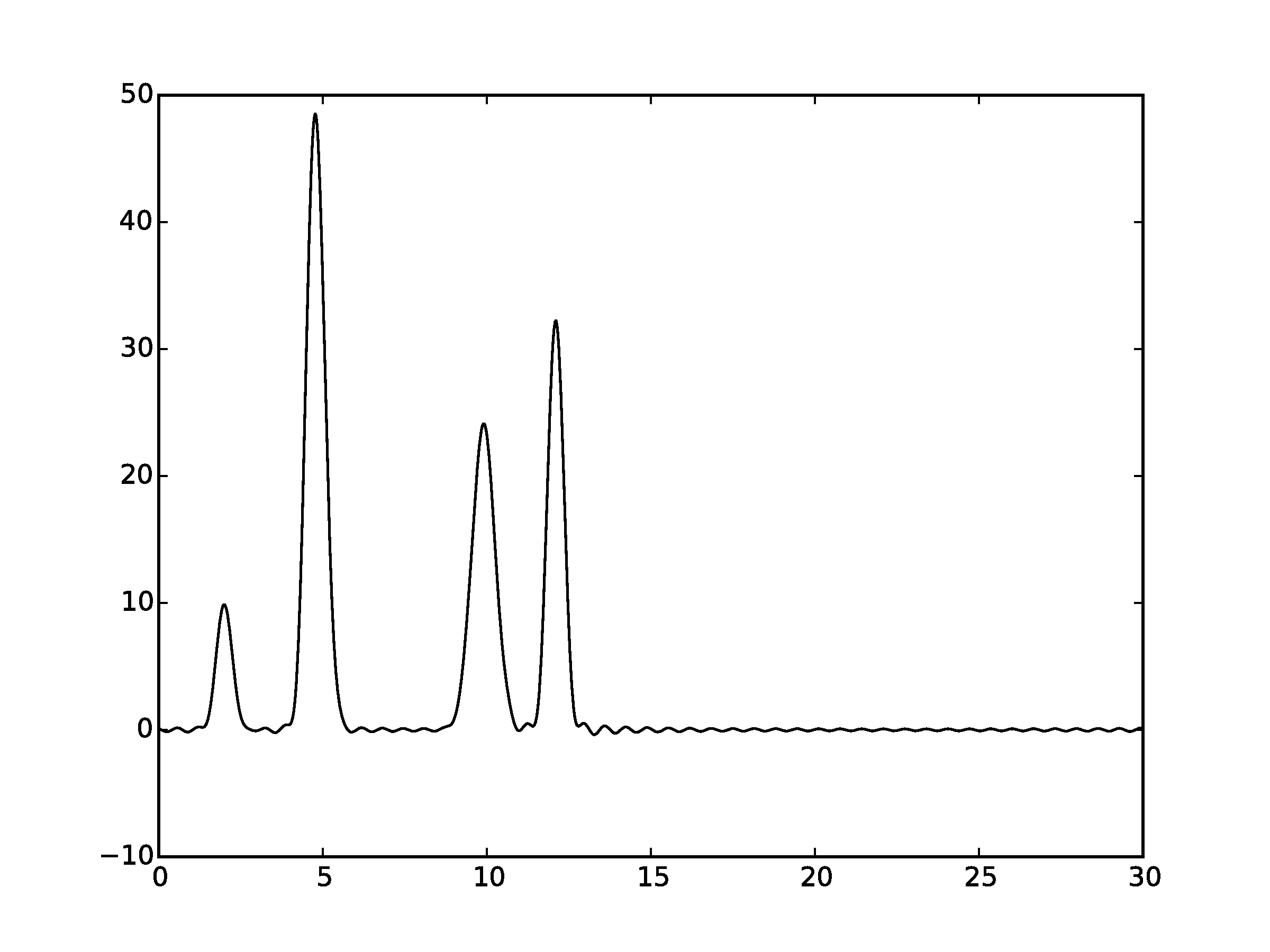
Рисунок 2.7Графики восстановленных функций, представленные пунктирной линией, для 45 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
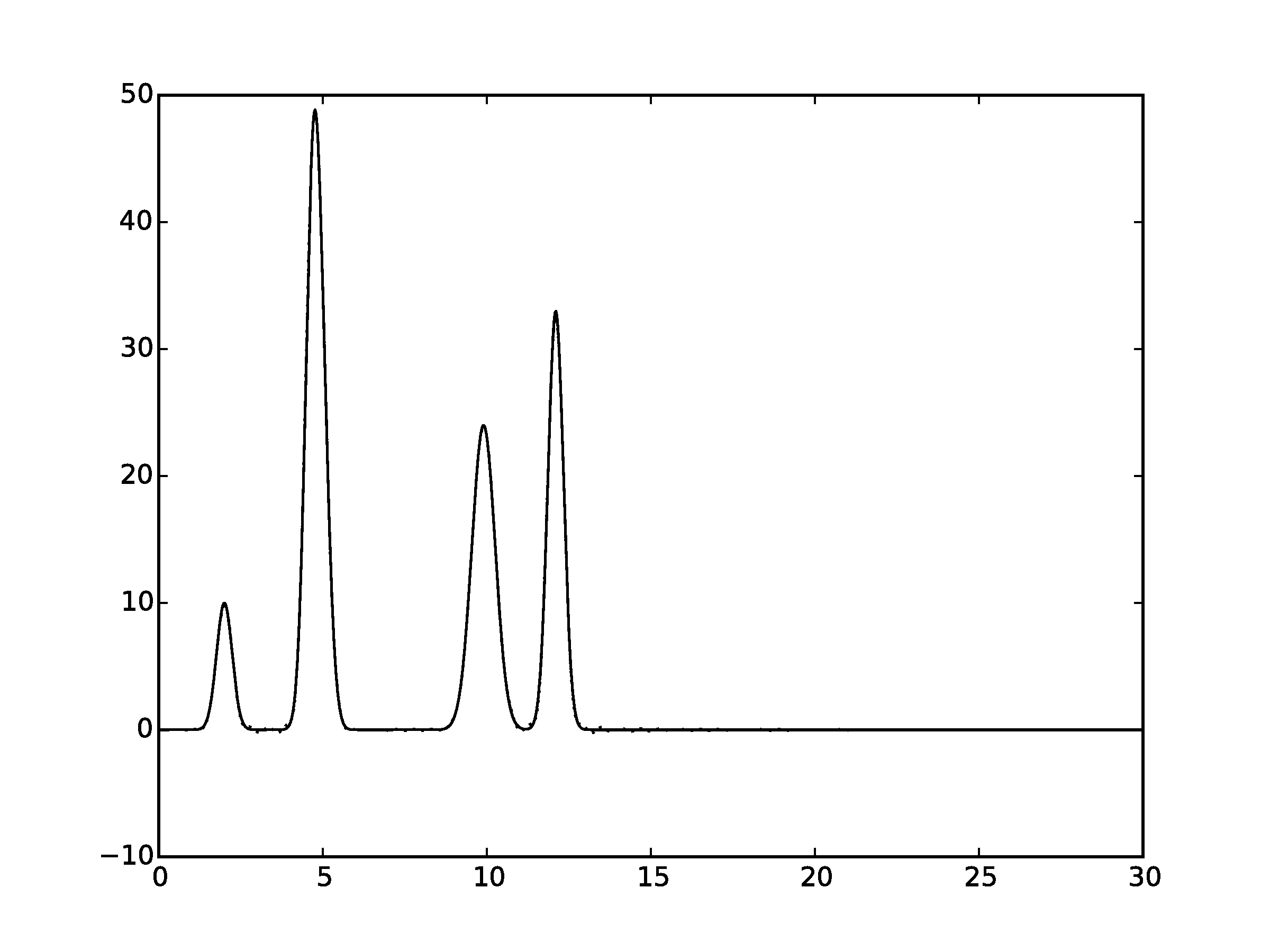
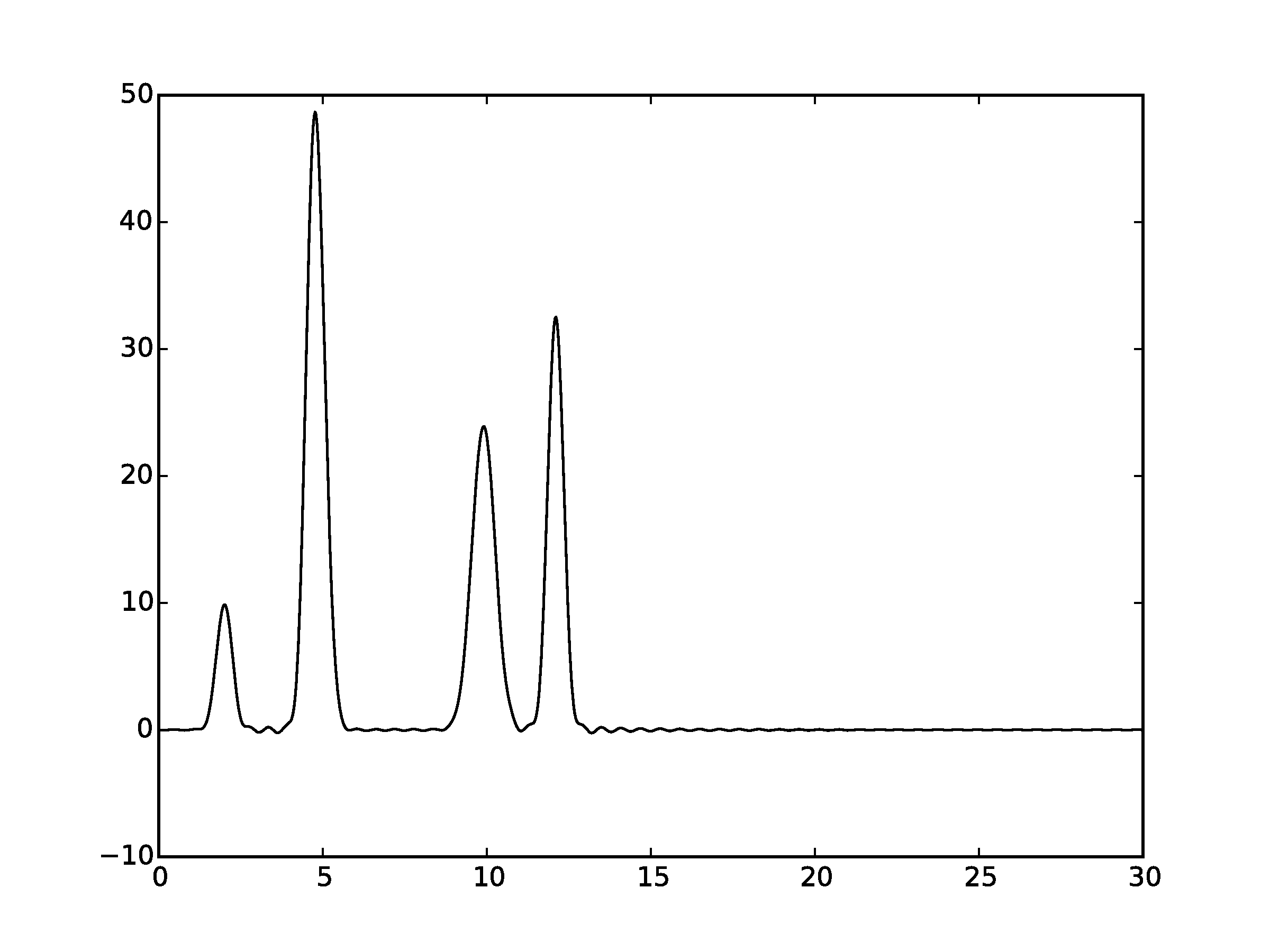
Рисунок 2.8Графики восстановленных функций, представленные пунктирной линией, для 49 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
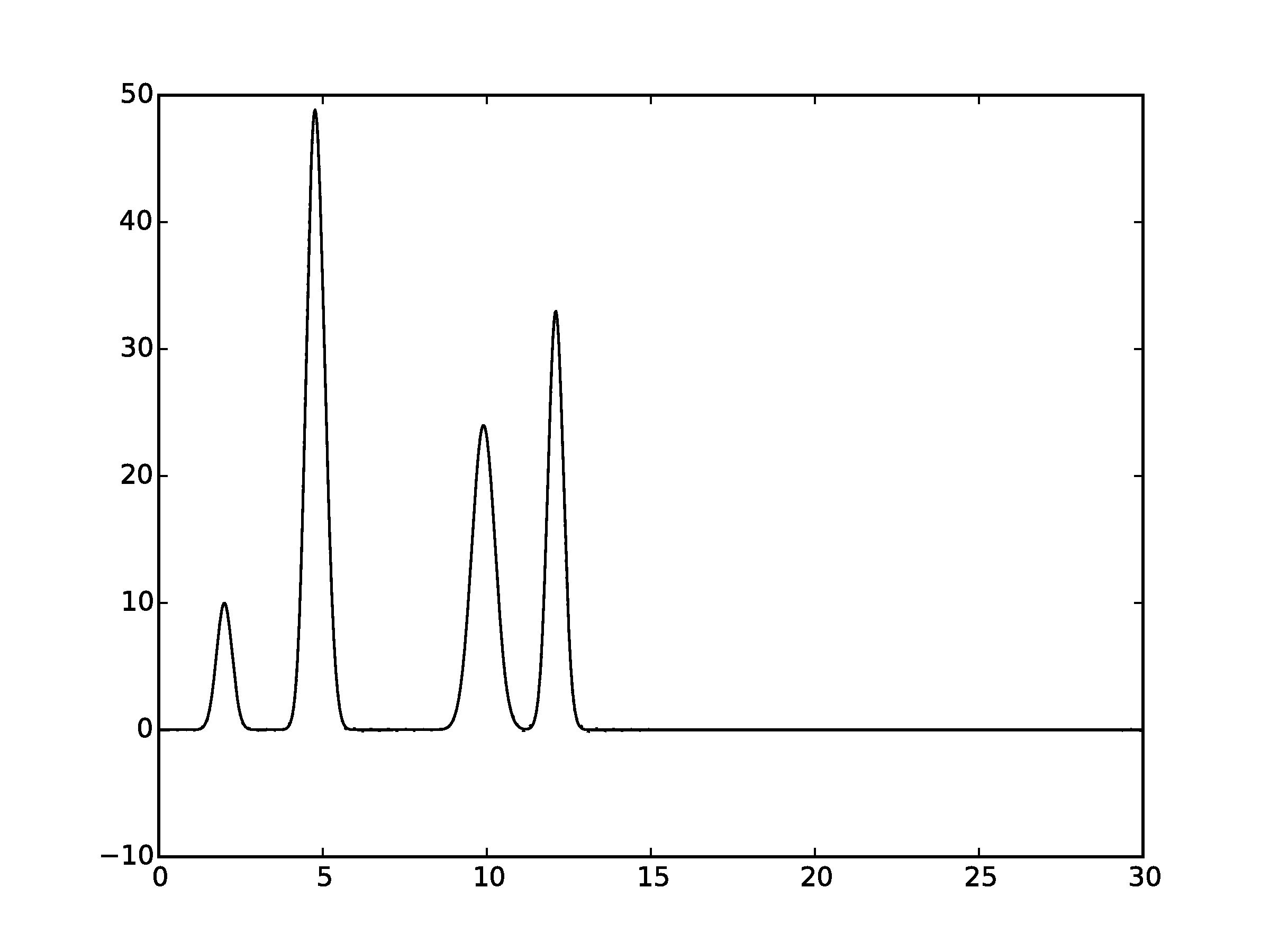
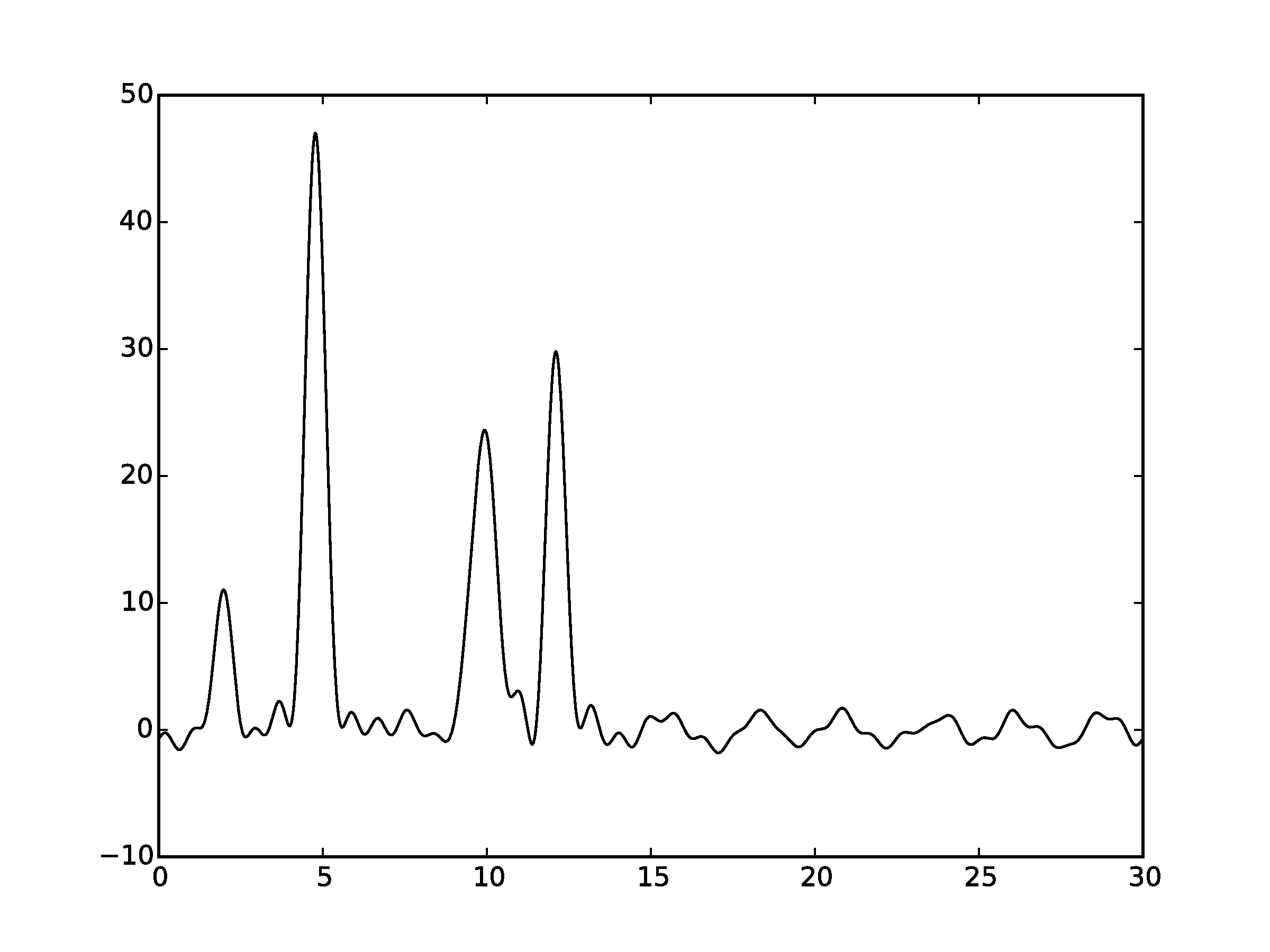
Рисунок 2.9Графики восстановленных функций, представленные пунктирной линией, для 50 гармоник. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
Договоримся оценивать востановленную функцию относительно исходной следующим образом:
Восстановление для n = 20 можно оценить как «среднее»: положение лишь некоторых атомов можно определить по восстановленной функции. Для n = 30 по восстановленной функции можно угадать положение всех максимумов, зная число слагаемых, однако на восстановленной функции максимумы некоторых «атомов» плохо отличимы от шума («хорошее восстановление»).
Затем при восстановлении по полному набору гармоник 0,..., 35 к амплитудам и фазам был добавлен шум (10% к амплитуде; 10% к фазе; по 10% к амплитуде и фазе):
python func2fourier.py -F 10 -i func.txt -o ft_noise10-0.txt; do
python fourier-filter.py -r 0-35 -i ft_noise10-0.txt -o ft_noise10-0_n0.txt; do
python fourier2func.py -i ft_noise10-0_n0.txt -o two_func_noise10-0_n0.txt;
do mv 13.pdf ./nose10.pdf
python func2fourier.py -P 10 -i func.txt -o ft_noise10-0.txt; do
python fourier-filter.py -r 0-35 -i ft_noise10-0.txt -o ft_noise10-0_n0.txt; do
python fourier2func.py -i ft_noise0-10_n0.txt -o two_func_noise10-0_n0.txt;
do mv 13.pdf ./nose10.pdf
python func2fourier.py -F 10 -P 10 -i func.txt -o ft_noise10-0.txt; do
python fourier-filter.py -r 0-35 -i ft_noise10-10.txt -o ft_noise10-10_n0.txt; do
python fourier2func.py -i ft_noise10-10_n0.txt -o two_func_noise10-10_n0.txt;
do mv 13.pdf ./nose10_10.pdf
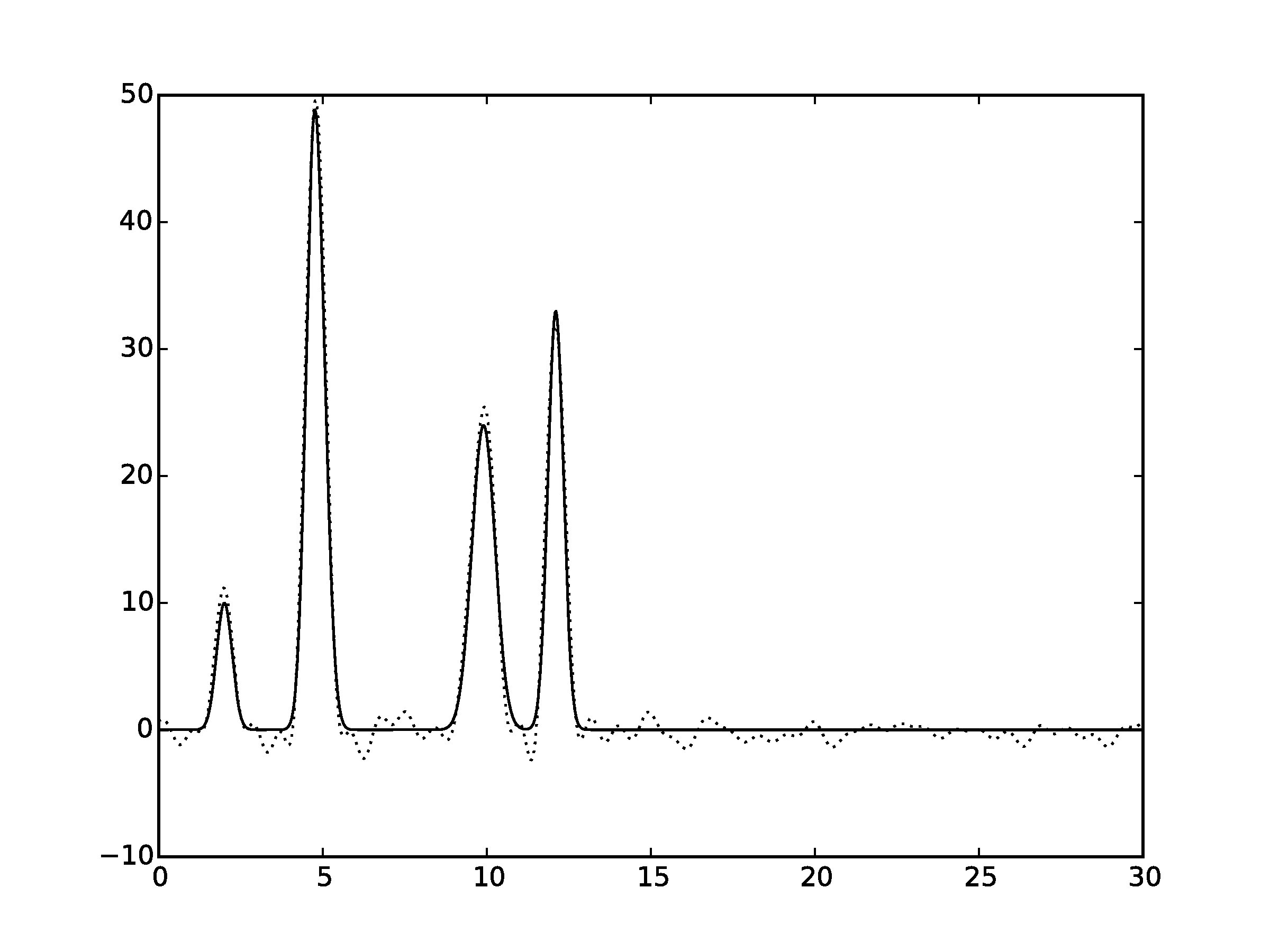
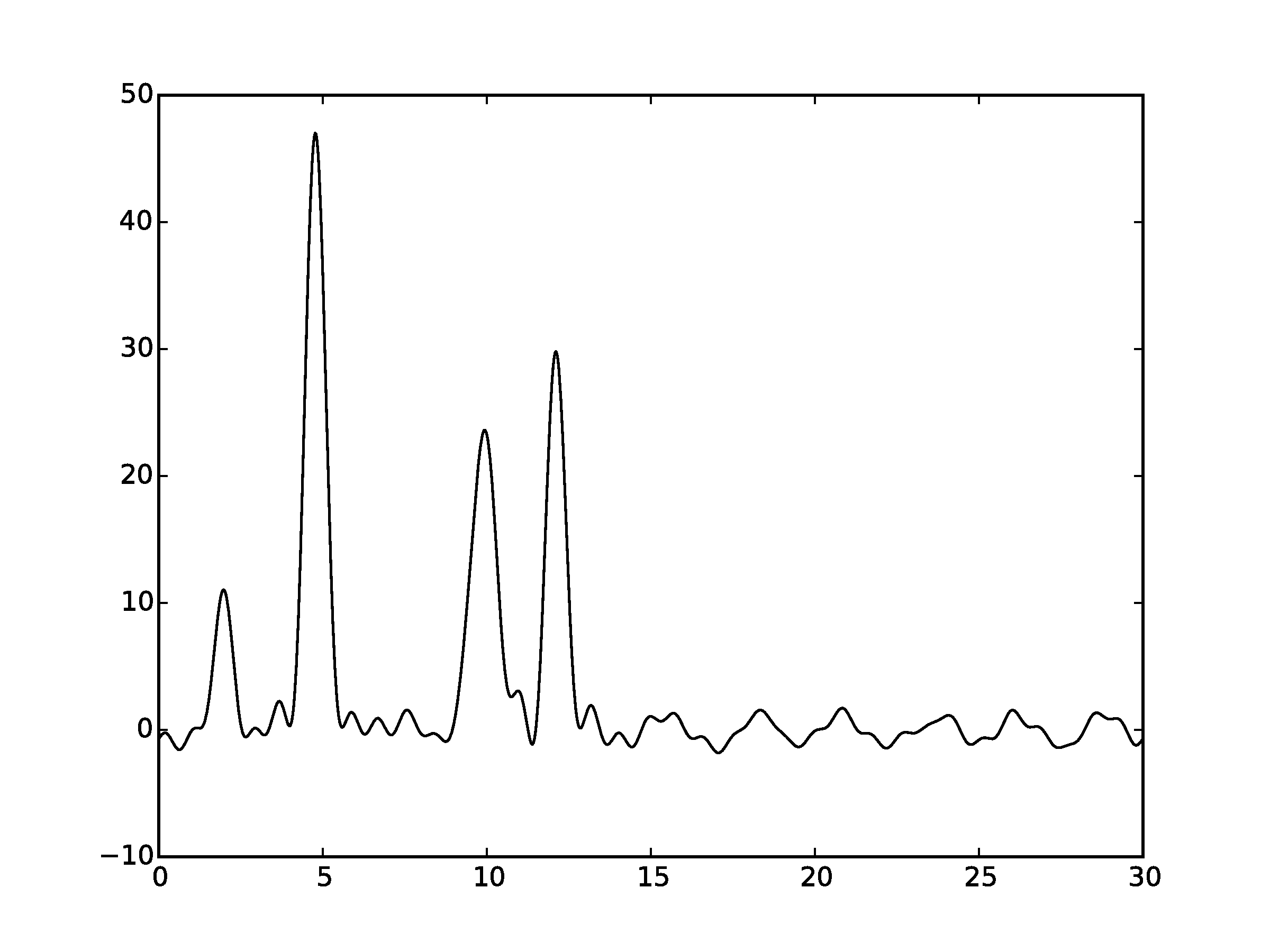
Рисунок 3.1Графики восстановленных функций, представленные пунктирной линией, для 35 гармоник с добавлением шума 10% к амплитуде. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
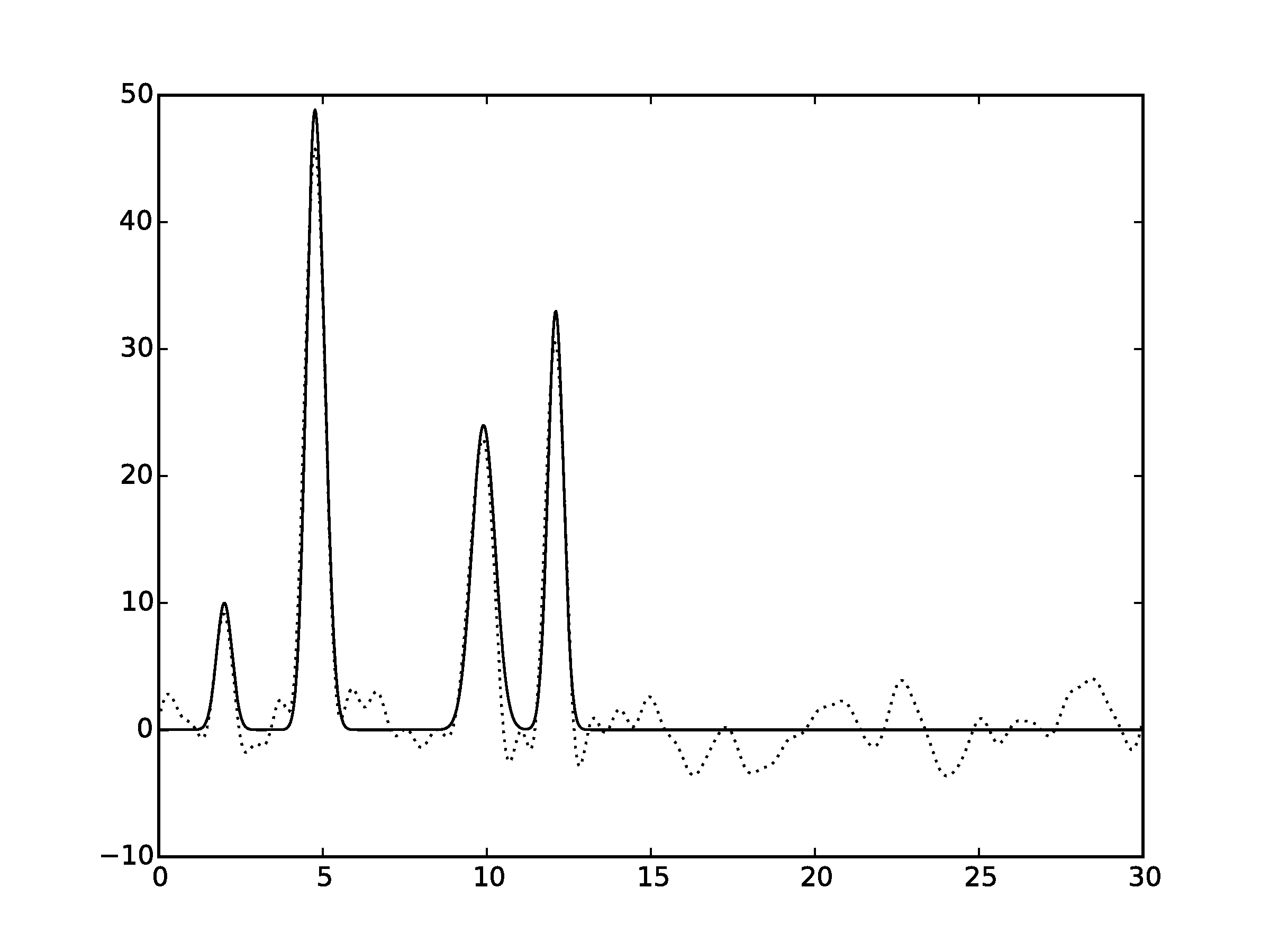
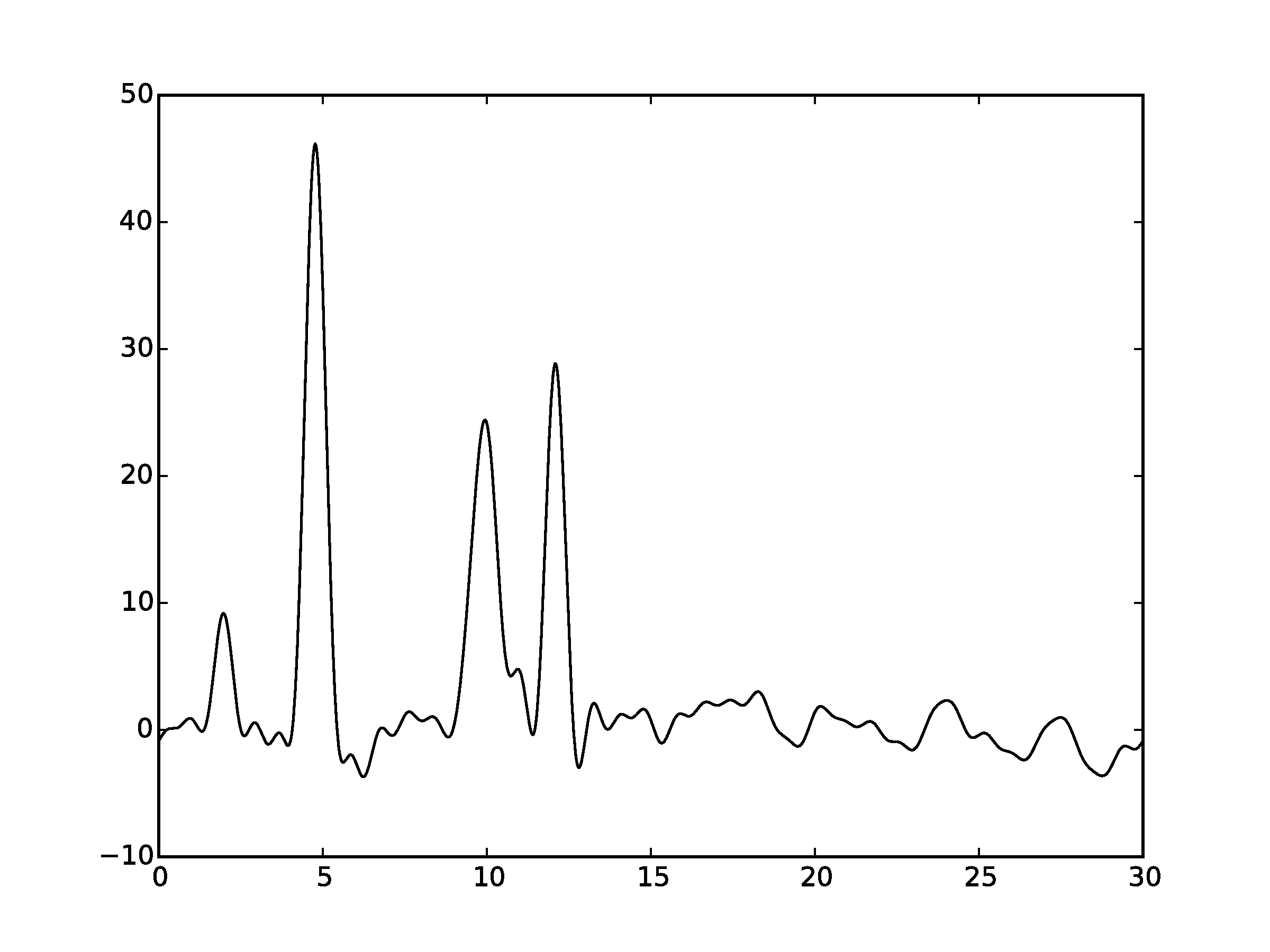
Рисунок 3.2Графики восстановленных функций, представленные пунктирной линией, для 35 гармоник с добавлением шума 10% к фазу. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
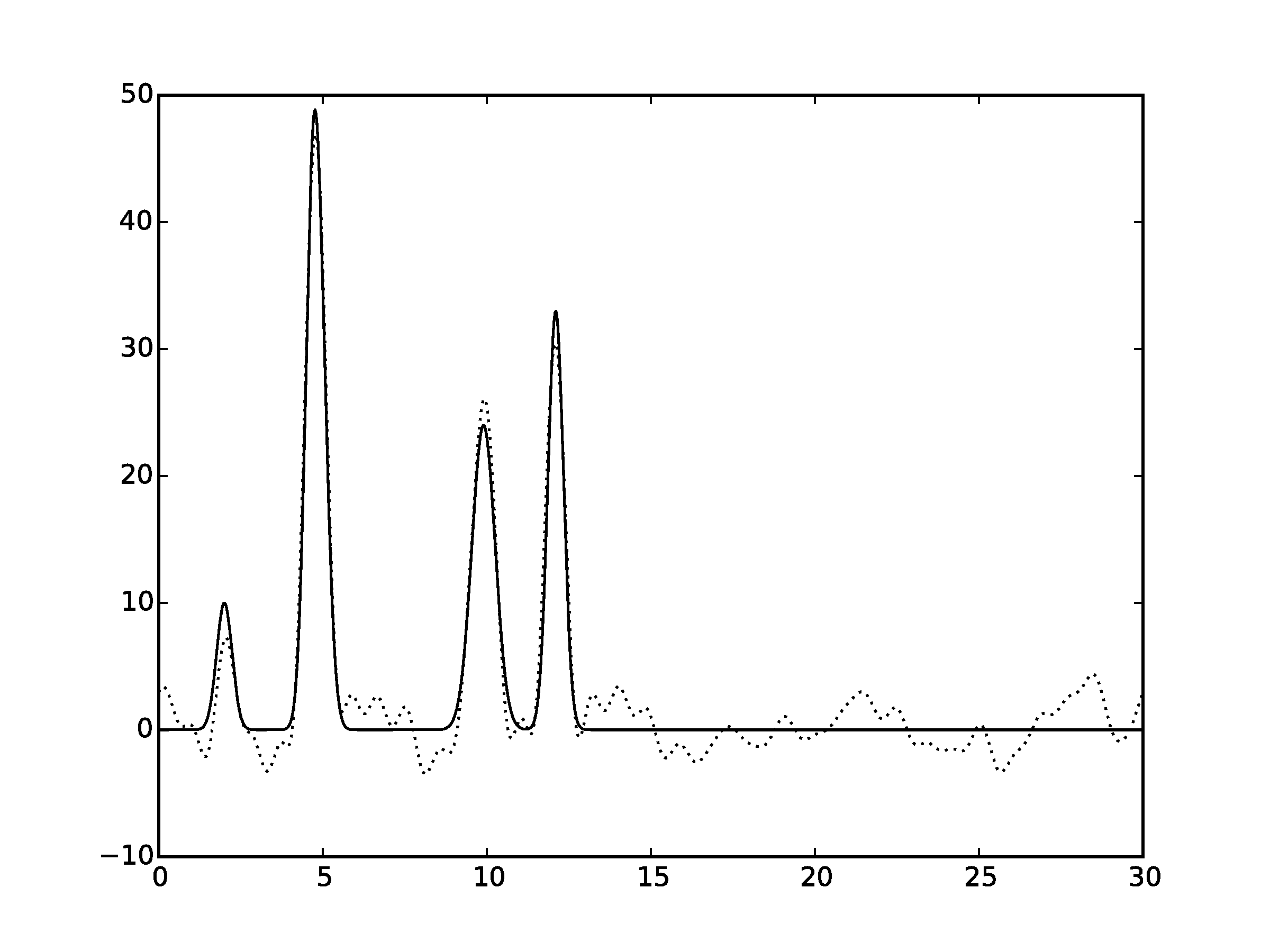
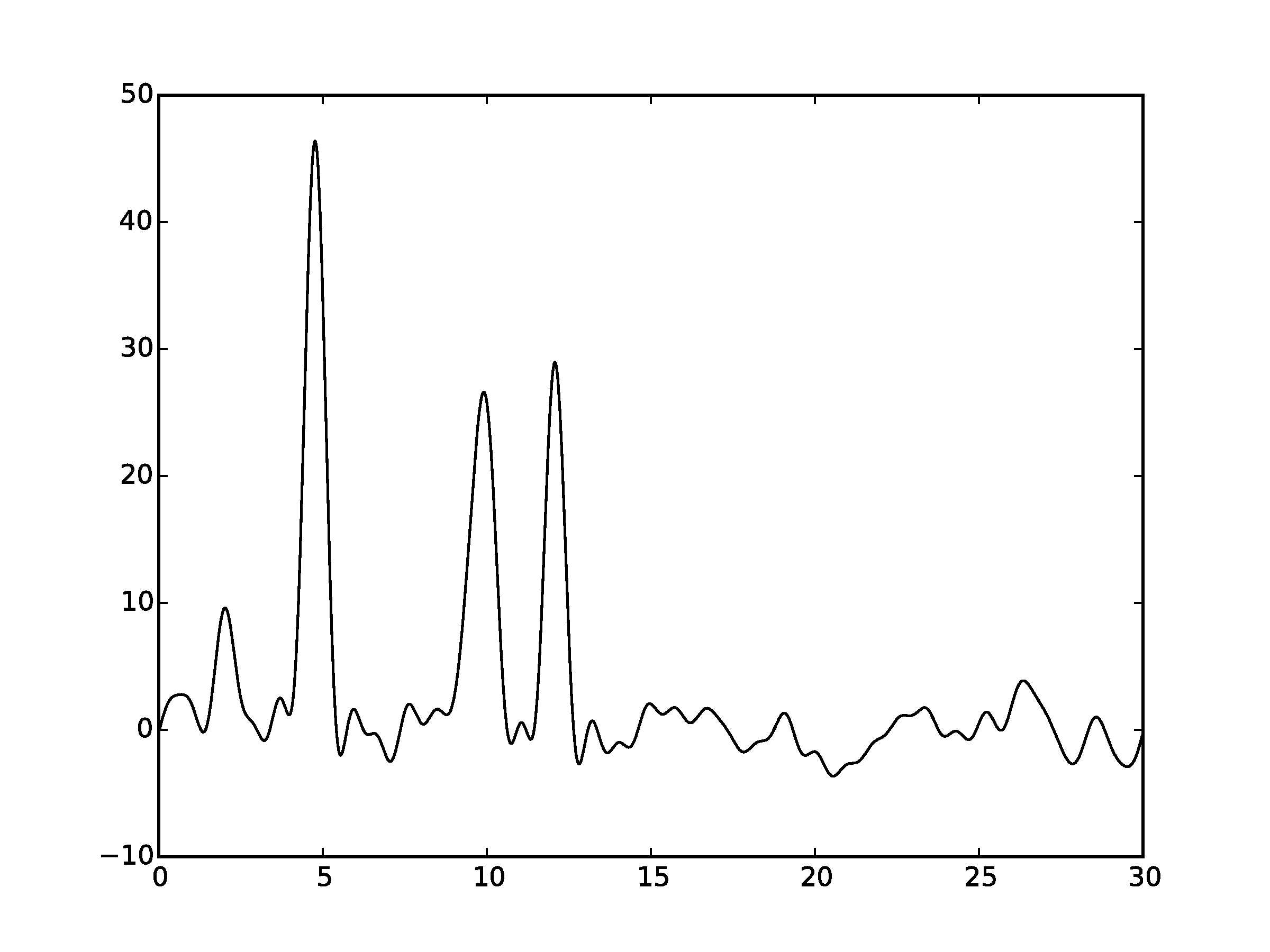
Рисунок 3.3Графики восстановленных функций, представленные пунктирной линией, для 35 гармоник с добавлением шума 10% и к амплитуде, и к фазе. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
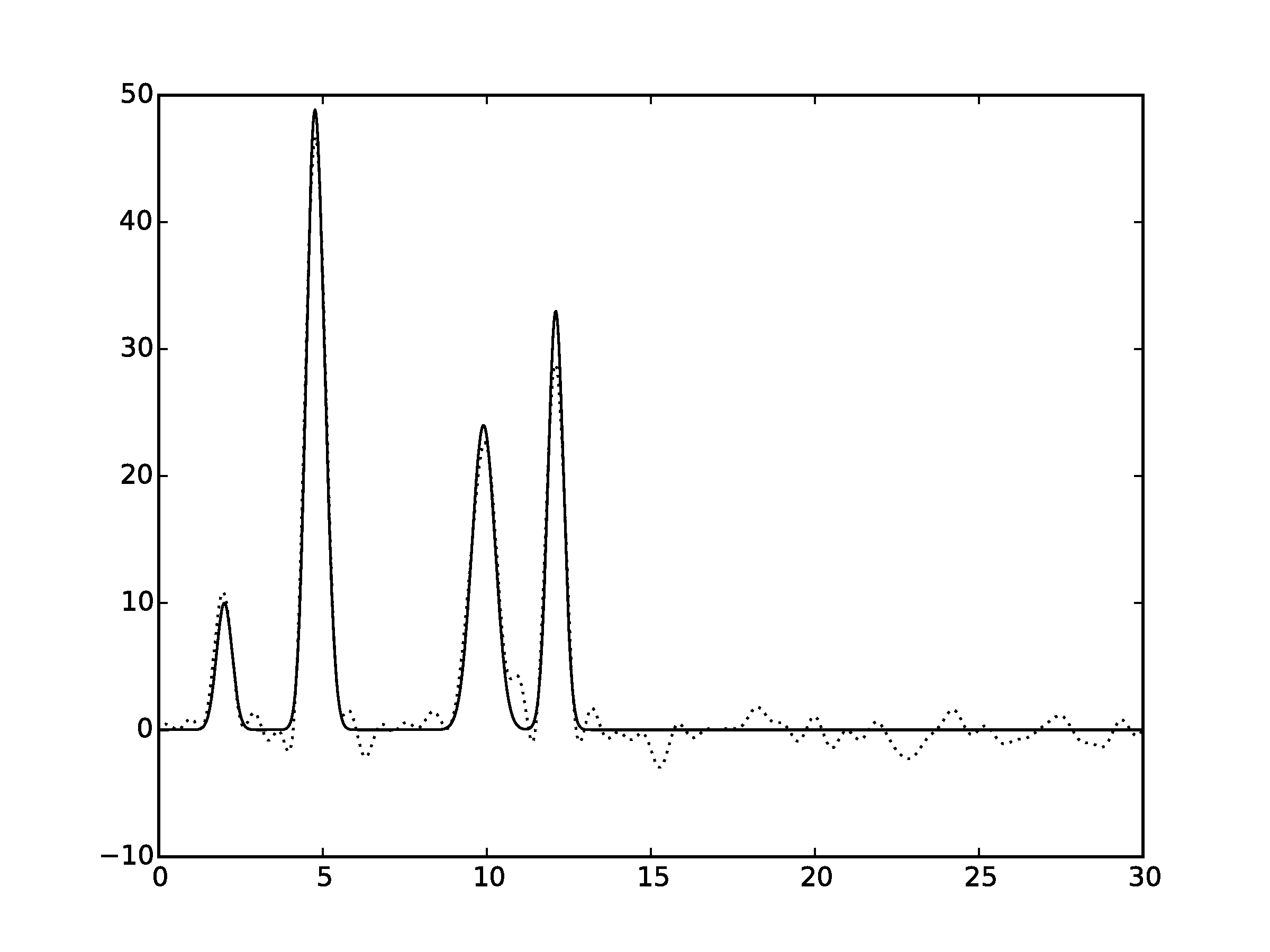
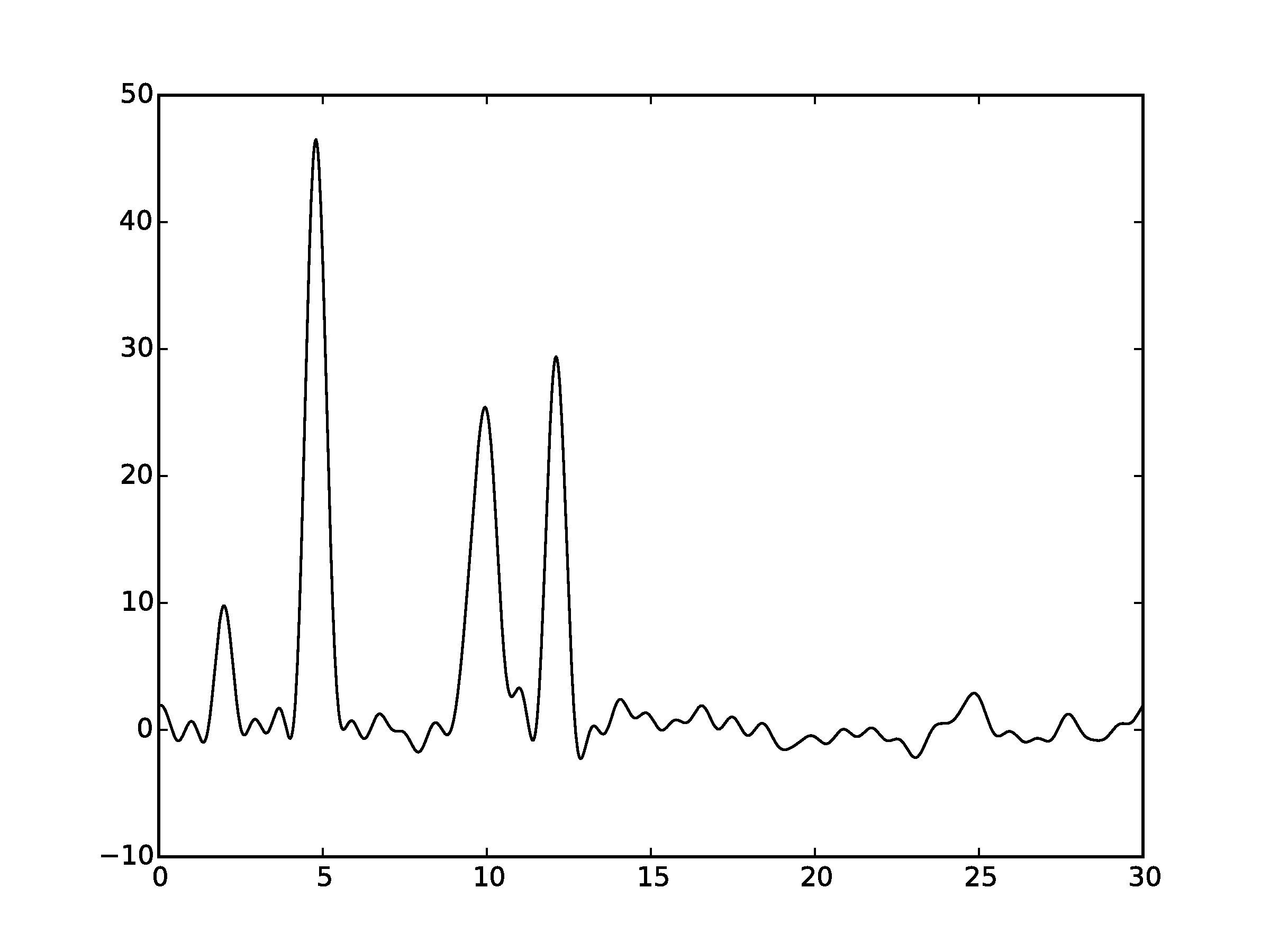
Рисунок 3.4Графики восстановленных функций, представленные пунктирной линией, для 35 гармоник с добавлением шума 7% и к амплитуде, и к фазе. Исходная функция – представлена в виде сплошной линии. (С права график без исходной функции)
Шум снижает качество востановления. Стоит отметить, что шум в фазах вносит больше вклада в изменения, чем шум в амплитудах. Как видно, при выбранных значениях шума (как для амплитуды, так и для фазы) становится невозможным восстановление всех положений максимумов гауссовых функций. Для более низких значений шума (по 7% к амплитуде и фазе) положения максимумов угадываются («хорошее восстановление»).
Неполные наборы гармоник
Для получения неполного набора гармоник были применены следующие команды
#удаление первых двух гармоник
python fourier-filter.py -r 2-35 -i func_ft.txt -o ft_2-35.txt
python fourier2func.py -i ft_2-35.txt -o two_func_2-35.txt
do mv 13.pdf ./garm_2.pdf
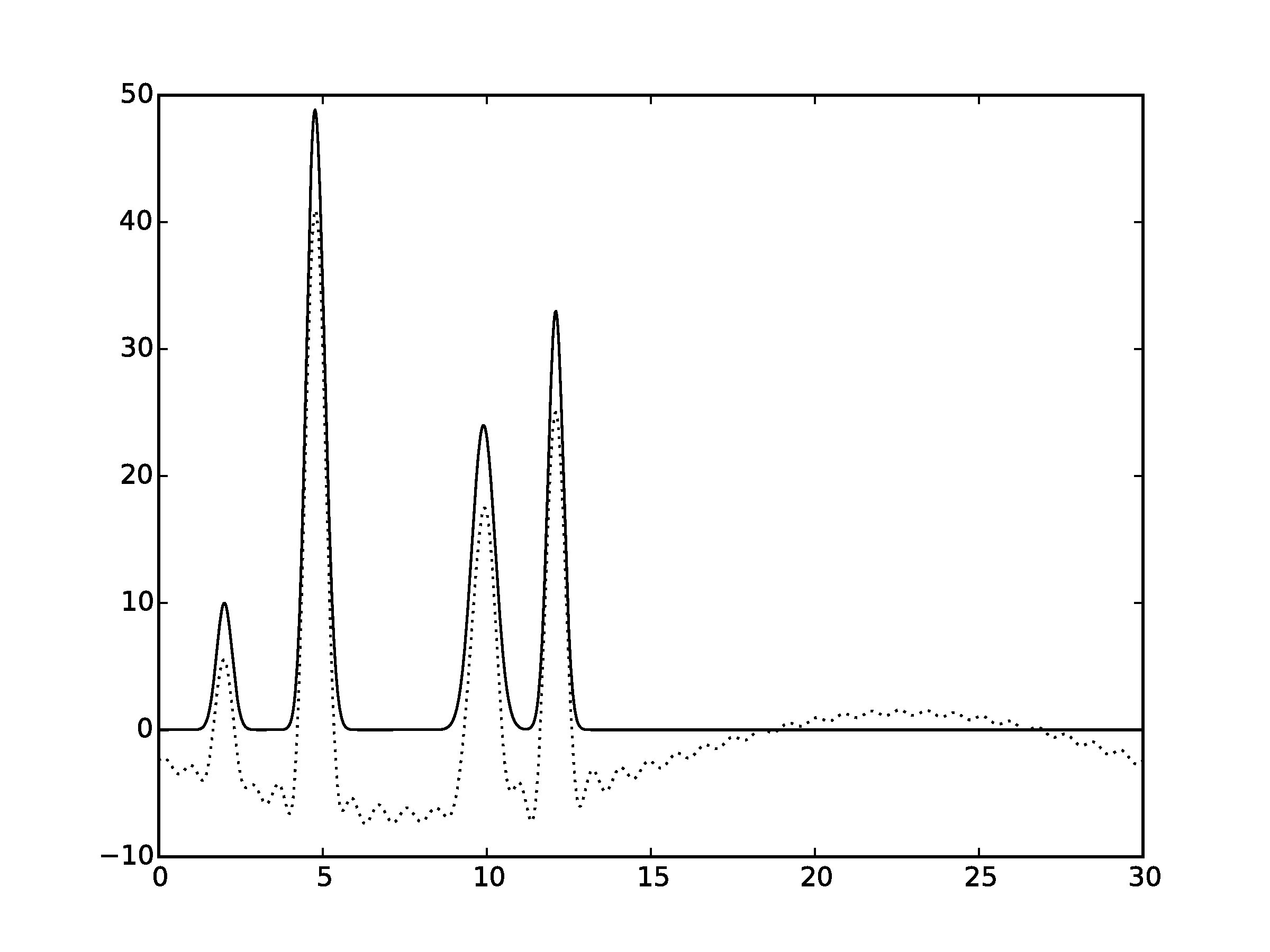
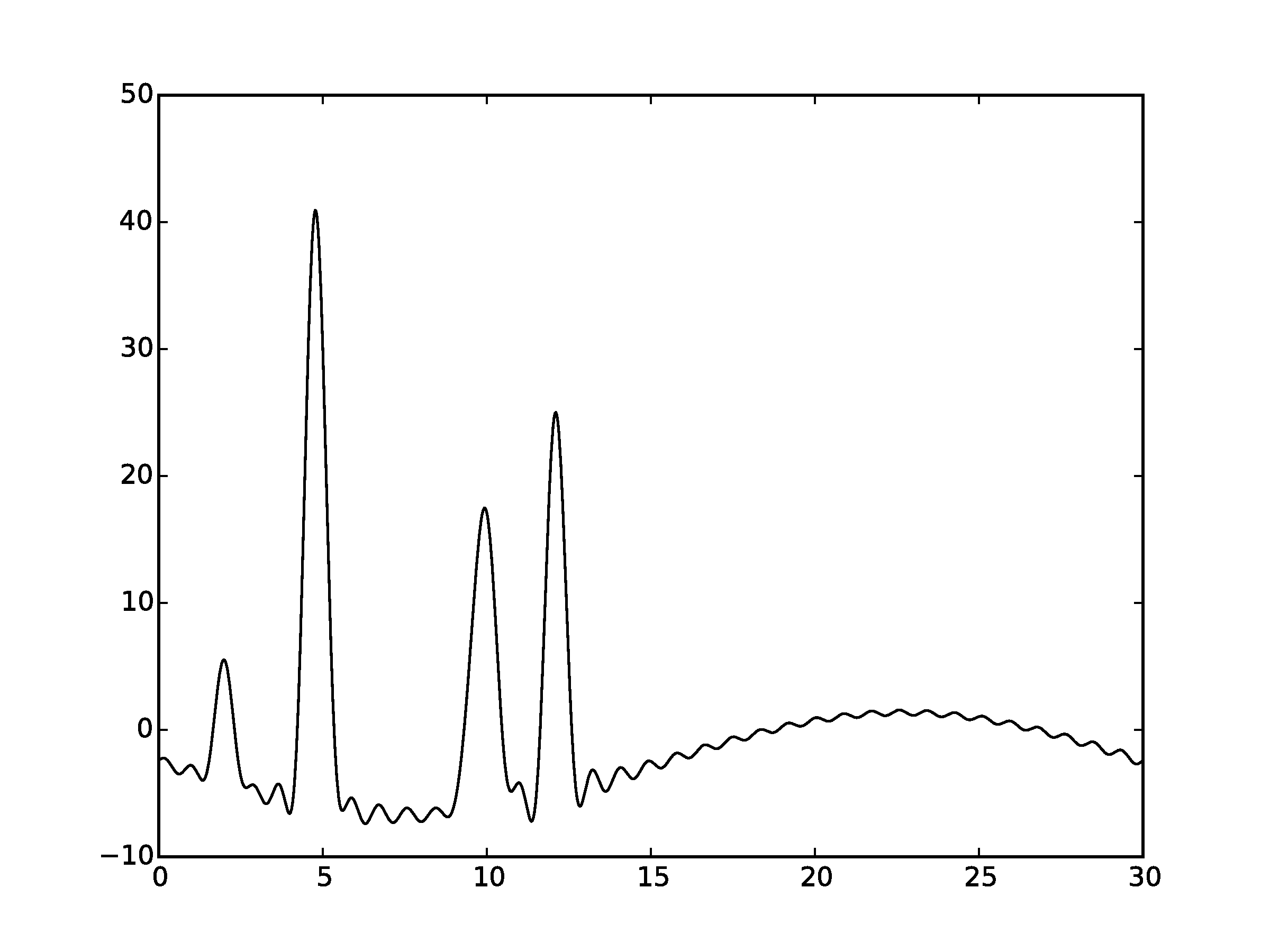
Рисунок 4.1Графики восстановленных функций с неполным набором гармоник 2-35 (пунктирная линия) и исходной функци (сплошная линия). (С права график без исходной функции)
Для получения неполного набора гармоник без ~11% гармоник в его середине были удалены гармоники с номерами 11 - 14, гармоники с номерами 10 - 15).
python fourier-filter.py -r 0-10,15-35 -i func_ft.txt -o ft_0-10_15-35.txt;
python fourier2func.py -i ft_0-10_15-35.txt -o two_func_0-10_15-35.txt;
mv 13.pdf ./garm_14.pdf
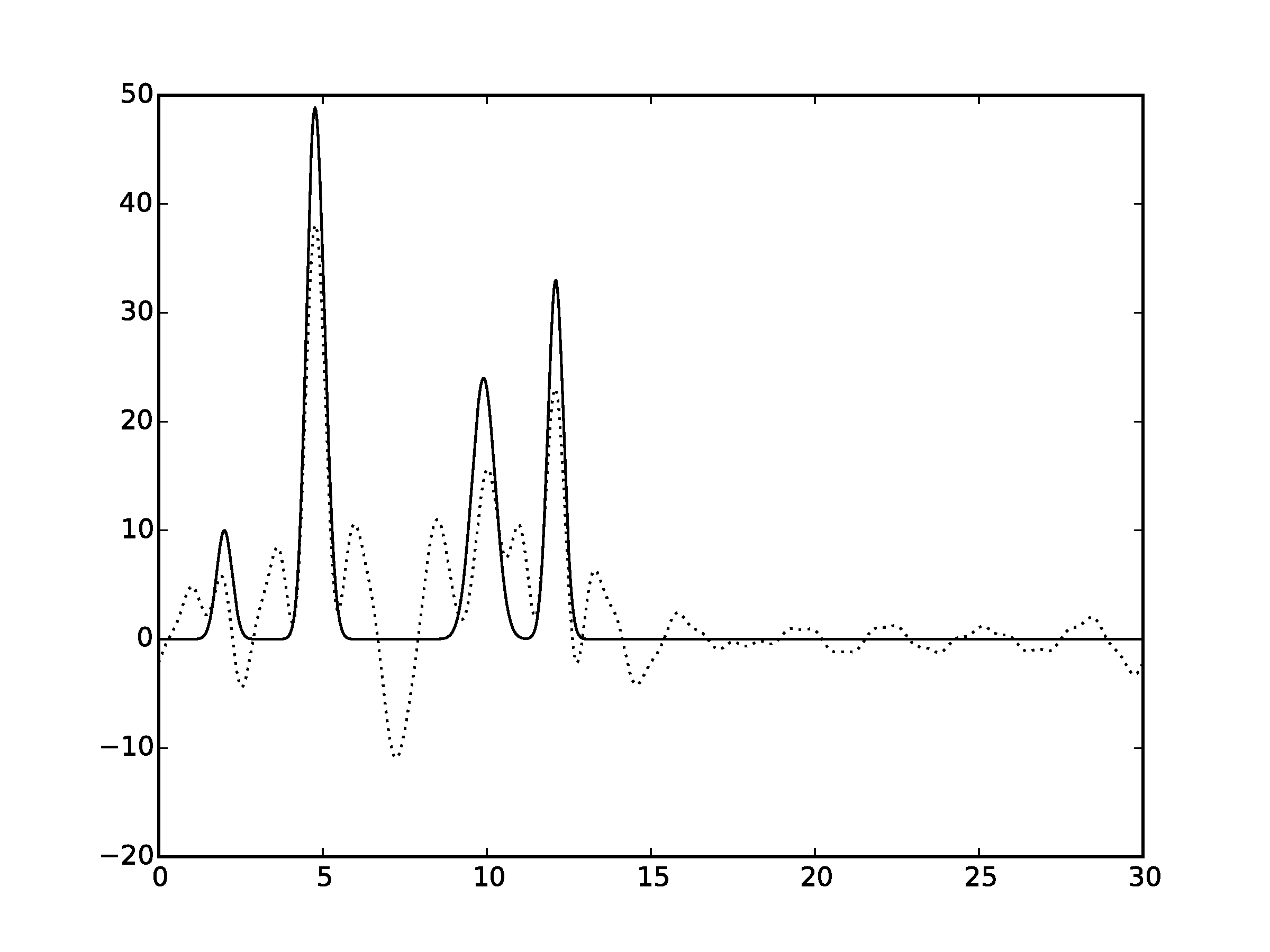
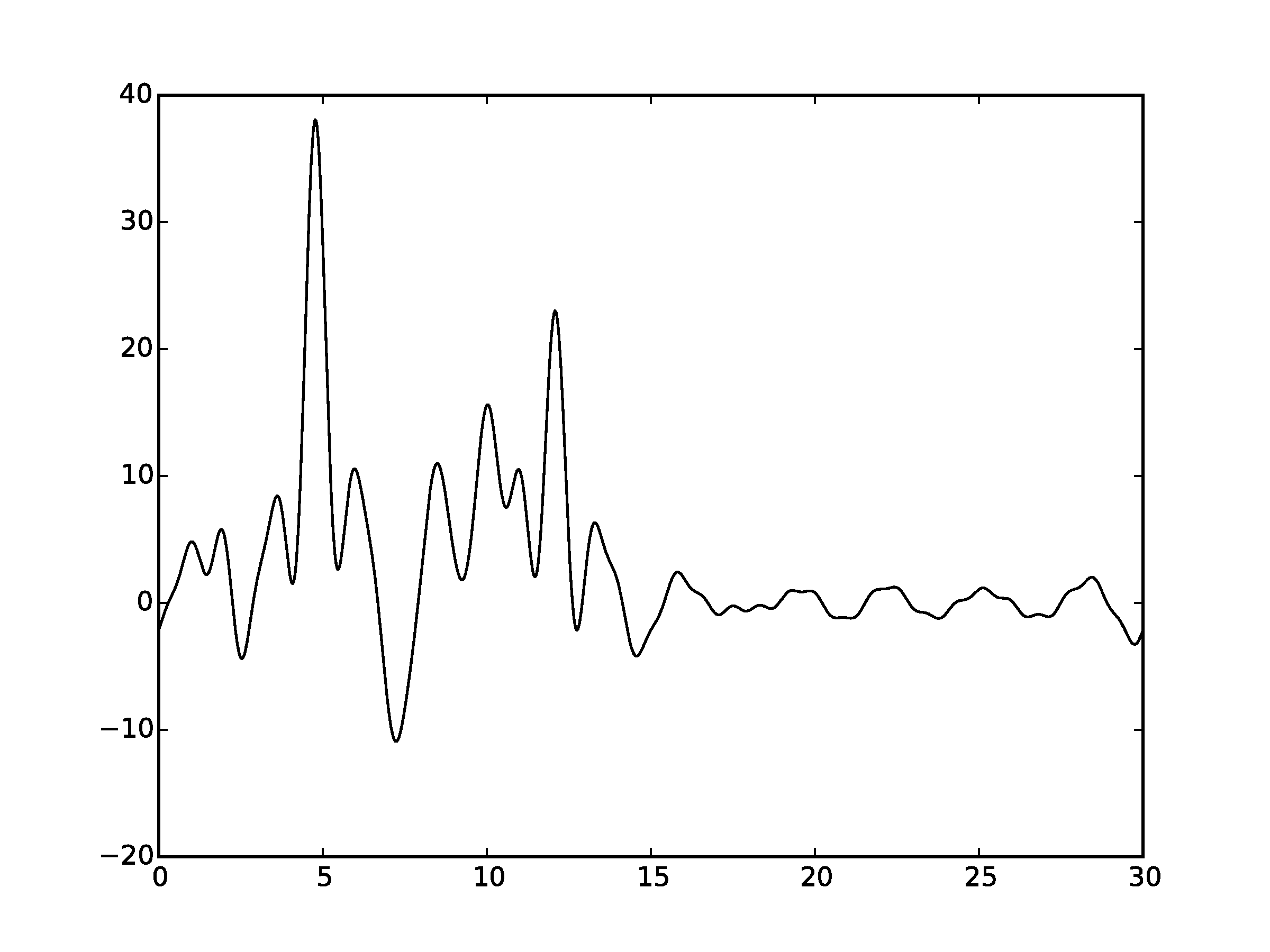
Рисунок 4.2Графики восстановленных функций с неполным набором гармоник 0-10 и 15-35 (пунктирная линия) и исходной функци (сплошная линия). (С права график без исходной функции)
К набору гармоник 0, 1, ..., 35 была добавлена гармоника 55:
python fourier-filter.py -r 0-35,55 -i func_ft.txt -o ft_0-35_55.txt;
python fourier2func.py -i ft_0-35_55.txt -o two_func_0-35_55.txt; mv 13.pdf ./gram55.pdf
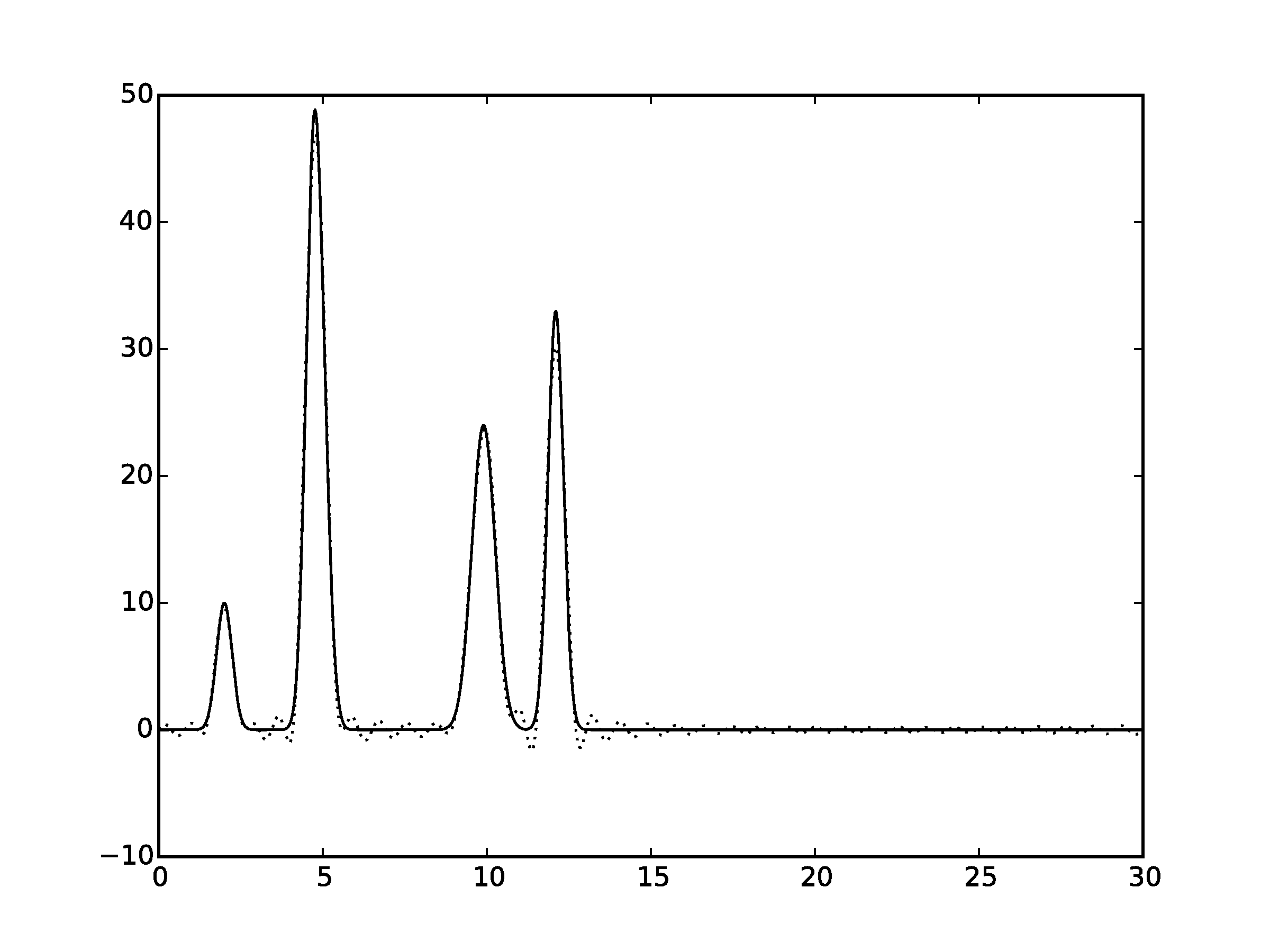
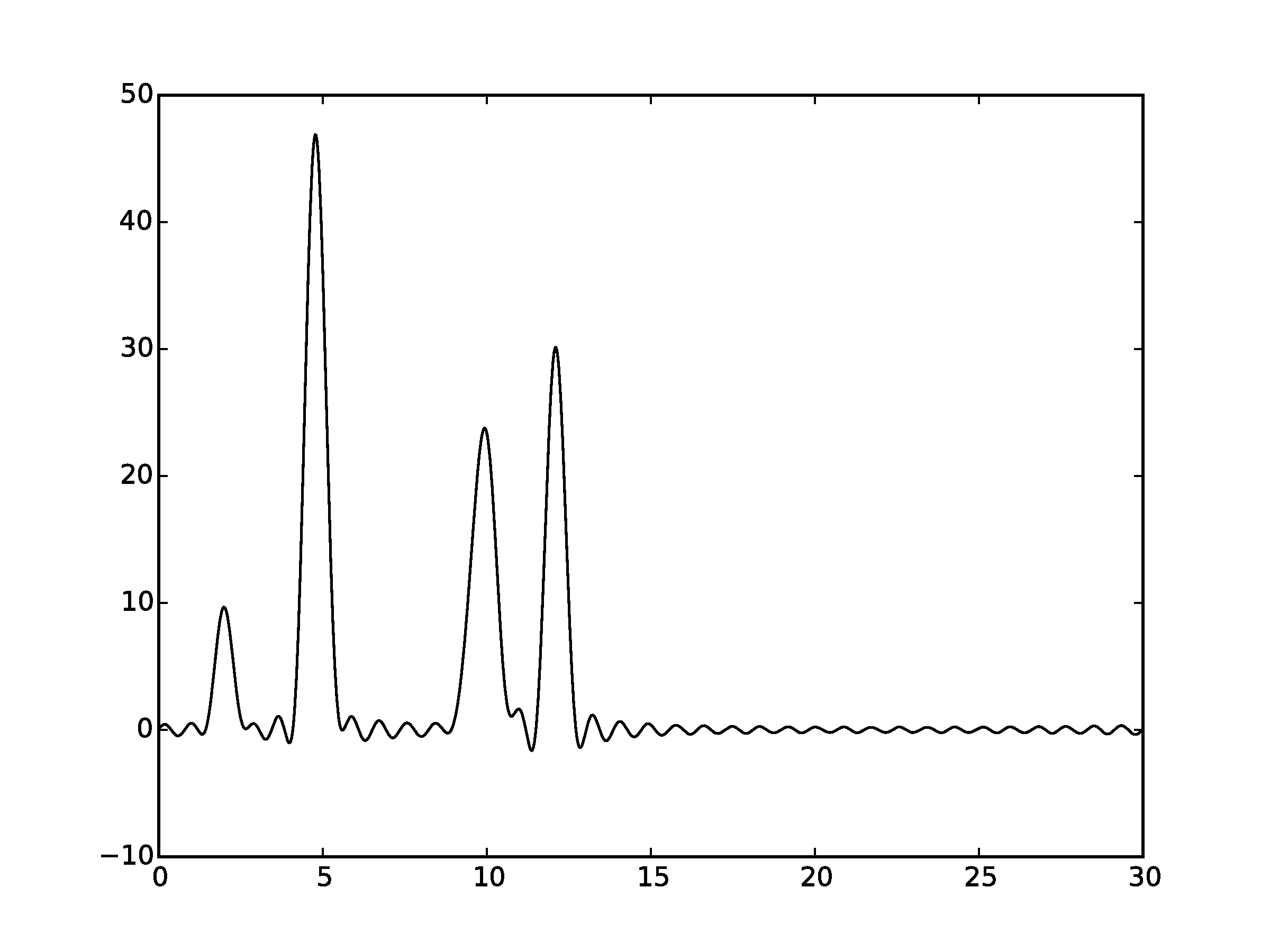
Рисунок 4.2Графики восстановленных функций с неполным набором гармоник 0-35и 55 (пунктирная линия) и исходной функци (сплошная линия). (С права график без исходной функции)
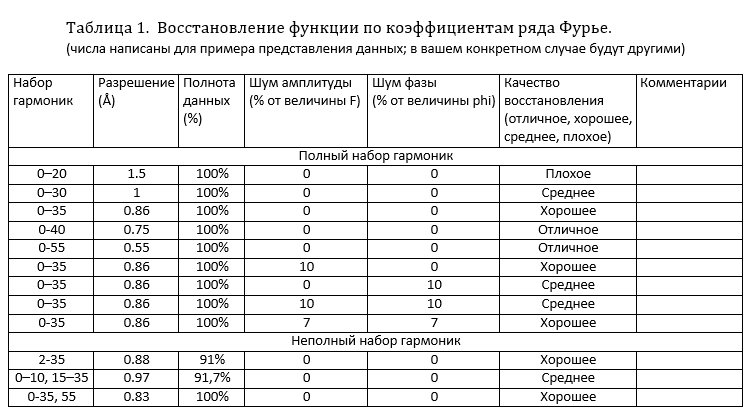
Определение разрешения набора гармоник
Разрешение для полного набора гармоник 0, 1, ..., 40 равно 30 Å / 41 ≈ 0,75 Å (в данном компьютерном эксперименте). Полнота данных вычисляется как процент гармоник в наборе, период которых не меньше разрешения, от числа гармоник в полном наборе для этого разрешения. Для полного набора полнота данных равна 100%. Для неполного набора гармоник разумно всегда указывать, помимо разрешения, полноту данных. Следует понимать, что для неполного набора данных нет строгого определения разрешения и поэтому могут возникать неоднозначные ситуации. Например, если применить определение разрешения для полного набора гармоник к набору 0, ..., 40, 50, то разрешение составит ∼0.6 , а полнота данных – 80%. Но в данной ситуации наиболее целесобразным представляется принять разрешение в ∼0.75 Å. Поэтому имеет смысл вводить порог по полноте данных (напимер, в 90%), при котором "выбивающиеся" отсеиваются и делается перерасчет разрешения и полноты данных.