| Главная |
| Семестры |
| О себе |
| Ссылки |
1. Задание функции
Для выполнения задания рассмотрим две гипотетические взаимодействующие одномерные молекулы на отрезке 0-30 Ангстрем, электронные плотности которых описываются комбинацией гауссовых кривых с пиками в районе ядер атомов (рис. 1А):
python compile-func.py -g 14,3,2.5+15,3,3.5+13,3,5+2,3,8.5+17,3,9.5+2,3,11
python func2fourier.py -i func.txt -o fourier_funcs/full_500.txt
Можно подобрать координаты центров атомов так, чтобы в нашей системе было четыре разных случая:
1. Два атома, обладающие высоким максимумом электронной плотности, лежат на близком расстоянии.
2. Два атома, обладающие высоким максимумом электронной плотности, находятся далеко друг от друга.
3. Два атома, один из которых обладает низким максимумом электронной плотности, лежат на близком расстоянии.
4. Два атома, один из которых обладает низким максимумом электронной плотности, находятся далеко друг от друга.
Электронная плотность является интегрируемой функцией, следовательно, ее можно разложить в ряд Фурье. Это используется в рентгеноструктурном анализе для получения непрерывного приближения электронной плотности. Ряд Фурье обладает достаточно быстрой сходимостью, и первых пятисот его членов с большим запасом хватает для получения картины электронной плотности, неотличимой от исходной (рис. 1В). Если посмотреть на полученный файл с коэффициентами Фурье, то можно заметить, что амплитуды всех гармоник после сороковой меньше 0.1, а амплитуды всех гормоник после семидесятой меньше 0.001.
| А. Исходная функция электронной плотности | В. Функция электронной плотности, восстановленная с помощью 500 первых членов ряда Фурье |
 |
 |
Рисунок 1
2. Минимальный набор первых гармоник, необходимый для восстановления электронной плотности
Введем критерии качества приближения электронной плотности:
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех
гауссовых слагаемых функции ("атомов")
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя
на восстановленной функции максимумы от атомов не отличимы от шума
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать
примерный размер "молекулы"
Будем рассматривать две молекулы в системе по отдельности, а качество разрешения всей системы можно определить как
худшее из двух.
Постепенным увеличением количества гармоник, включаемых в аппроксимацию, можно получить все более хорошие разрешения (рис. 2).
| A. Гармоники 0-1 | B. Гармоники 0-5 | C. Гармоники 0-10 |
 |
 |
 |
| D. Гармоники 0-15 | E. Гармоники 0-20 | F. Гармоники 0-25 |
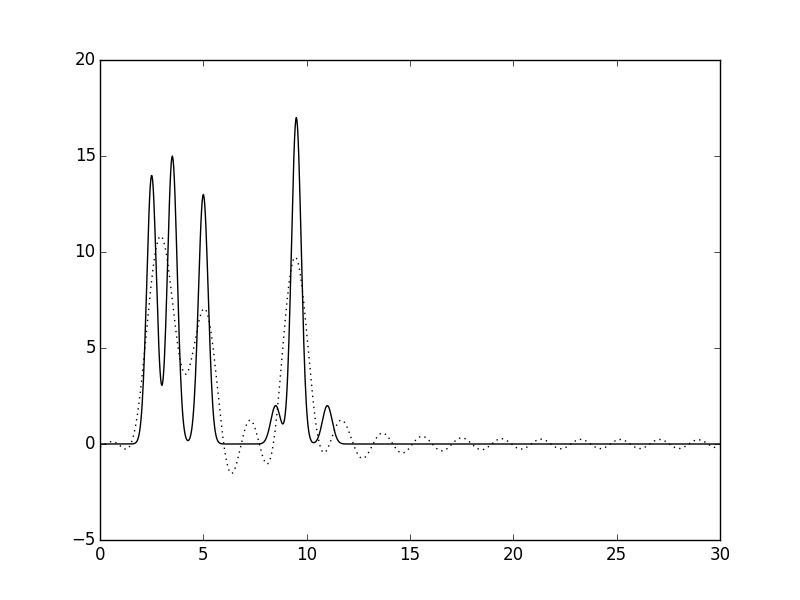 |
 |
 |
| G. Гармоники 0-30 | H. Гармоники 0-35 | I. Гармоники 0-40 |
 |
 |
 |
Рисунок 2. Постепенное увеличение числа гармоник в аппроксимации функции электронной плотности. Сплошной линией показана "настоящая" функция, а пунктиром -- ее аппроксимация.
Две молекулы на расстоянии 3.5 Ангстрем становятся различимыми уже при рассмотрении четырех-пяти гармоник.
Далее необходимо еще десять гармоник, чтобы в первой молекуле можно было различить атом с длинной связью. При рассмотрении
примерно двадцати первых гармоник, становится различим сигнал от бокового атома с длинной связью во второй молекуле: амплитуда
его сигнала становится выше средней амплитуды шума в 2 раза. При количестве гармоник, равном 25, становится различимым атом с
короткой связью в первой молекуле, но нужно еще пять гармоник, чтобы различить атом с такой же по длине связью во второй молекуле.
При дальнейшем увеличении количества гармоник до сорока, полученная из частичной суммы Фурье функция практически сливается
с заданной электронной плотностью.
Исходя из полученных данных, можно сказать, что атомы с длинными связями, но с маленьким максимумом электронной плотности, становятся
различимы раньше атомов с большим максимумом, но с малой длиной связи. Однако это может быть не справедливо для полных наборов данных.
3. Синтез Фурье из данных, содержащих шум
Далее, в фазы и амплитуды коэффициентов Фурье был внесен нормально распределенный шум. Результаты можно видеть на рисунке 3.
| F\φ | 0% | 10% | 20% | 40% |
| 0% |  |
 |
 |
 |
| 10% | 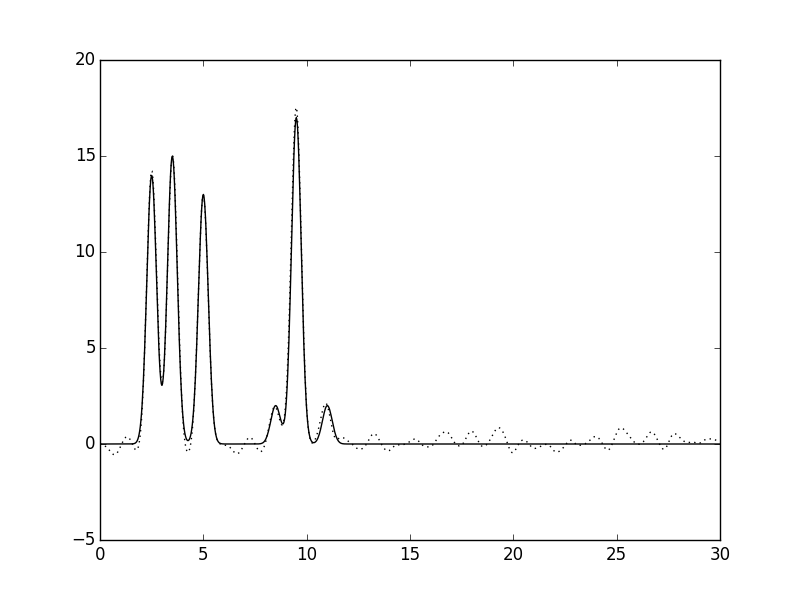 |
 |
 |
 |
| 20% |  |
 |
 |
 |
| 40% |  |
 |
 |
 |
Рисунок 3. Формы приближений в зависимости от уровня шума в данных. Слева направо увеличивается шум в фазе, а сверху вниз -- в амплитуде.
Можно заметить, что добавление даже небольшого шума в фазу сильно искажает картину, а вто время, как даже при уровне шума в амплитуде в 20% все еще различимы даже малые атомы. Также следует отметить, что, даже при высоких уровнях шума, атомы с большими пиками электронной плотности достаточно хорошо различимы.
4. Неполные данные
На практике, при расшифровке рентгеноструктурных данных, всегда работают с неполными наборами гармоник. На рисунке 4 показаны эффекты удаления разных наборов гармоник.
| A. Гармоники 1-40 | B. Гармоники 2-40 | |
| Удаление начальных гармоник |  |
 |
| С. Гармоники 5-40 | D. Гармоники 10-40 | |
 |
 |
|
| E. Гармоники 0-10+15-40 | F. Гармоники 0-20+25-40 | |
| Удаление гармоник среднего разрешения |  |
 |
| G. Гармоники 0-20+35-40 | ||
| Добавление гармоник высокого разрешения к набору гармоник низкого разрешения |  |
Рисунок 4. Формы приближений при неполных наборах гармоник.
Можно заметить, что, при удалении гармоник 0-5, все атомы различимы, что весьма хорошо для РСА, так как именно первые гармоники, соответствующие слабым векторам рассеяния, учесть не удается. При удалении средних гармоник, возникает большое количество высокочастотного шума, и малые атомы становится сложно от него отличить. При добавлении высокочастотных гармоник к набору с низким разрешением ничего принципиально не изменяется, так как высокочастотные гармоники имеют низкую амплитуду и не могут принципиально улучшить картину. Также заметим, что во всех случаях крупные атомы различимы.
В заключение, можно сказать, что Преобразование Фурье дает быстро сходящееся приближение к данным, которое, к тому же,
при удалении некоторых членов суммы, не дает совершенно другой картины, то есть оно устойчиво к потере данных.
Внесение шума в данные сильнее сказывается на результате в случае внесения шума в фазу, нежели в амплитуду. По этой
причине решение фазовой проблемы очень важно для рентгеноструктурного анализа.
Малые атомы (например, атомы водорода) легко детектировать, если иметь полный набор гармоник. При внесении шума и при
удалении некоторого количества данных, их сигналы теряются. По этой причине очень редко удается определить на структуре
атомы водорода.
Сравнительный анализ качества разрешения во всех случаях приведен в таблице 1.