Главная страница > Второй семестр > Филогенетические деревья

Филогенетические деревья, реконструированные разными способами

Реконструкция филогенетических деревьев проводилась по данным эталонного выравнивания сахароизомеризующих доменов (SIS, код доступа PF01380), взятого из базы данных Pfam (рис. 1). Были рассмотрены фрагменты пяти последовательностей глюкозамин — фруктоза-6-фосфатаминотрансферазы [изомеризующей], соответствующие данному домену:

GFA1_SCHPO 377-509 (Schizosaccharomyces pombe)

GLMS_HAEIN 288-421 (Haemophilus influenzae)

GLMS_ECOLI 288-421 (Escherichia coli)

GFA1_CANAL 391-523 (Candida albicans)

GLMS_BACSU 285-417 (Bacillus subtilis)

Приведенные выше белки являются ортологами, так как выполняют одинаковую функцию. Это позволяет рассматривать деревья, реконструированные для фрагментов последовательностей, как филогенетические деревья организмов, которым эти последовательности принадлежат (см. ниже).

Рис. 1. Эталонное выравнивание фрагментов последовательностей GFA1_SCHPO, GLMS_HAEIN, GLMS_ECOLI, GFA1_CANAL и GLMS_BACSU, соответствующих сахароизомеризующему домену.

Построение дерева по алгоритму UPGMA

Построение дерева проводилось по данным матрицы попарных совпадений последовательностей эталонного выравнивания. На основании этой матрицы была создана матрица эволюционных расстояний, элементы которой D_{i, j} вычислялись по формуле:
D_{i, j} = 1 - P_{i, j},
где P_{i, j} — элемент матрицы попарных совпадений (см. книгу UPGMA.xls, лист distances).
При построении дерева использовался алгоритм UPGMA. Каждая итерация алгоритма включает следующие шаги:

Выбор наименьшего элемента матрицы эволюционных расстояний (D_{x, y}).

Объединение соответствующих кластеров (X и Y).

Вычисление высоты нового кластера ρ_XY и длин созданных ребер L_x и L_y по формулам:
ρ_XY = 0.5 D_{x, y} ,
L_x = ρ_XY - ρ_X ,
L_x = ρ_XY - ρ_Y ,
где ρ_X — высота кластера X, ρ_Y — высота кластера Y.

Создание новой матрицы эволюционных расстояний, в которой эволюционное расстояние D_{xy, z} от нового кластера XY до любого другого кластера Z вычисляется как среднее арифметическое расстояний D_{x, z} и D_{y, z}.

Описанный выше алгоритм реализован с помощью электронной таблицы Excel (см. книгу UPGMA.xls, лист UPGMA). Правильная скобочная структура полученного дерева:

((GFA1_SCHPO:0.1250,GFA1_CANAL:0.1250):0.1763,((GLMS_HAEIN:0.1150,GLMS_ECOLI:0.1150):0.1788,GLMS_BACSU:0.2938):0.0075);
Дерево было визуализировано с помощью программ drawtree и drawgram. Программа drawtree построила неукорененное дерево (рис. 2А), а программа drawgram — укорененное (рис. 2Б). Наиболее информативным является укорененное дерево, так как правильная скобочная формула, полученная с помощью алгоритма UPGMA, содержит информацию о корне (при построении неукорененного дерева эта информация теряется).
По результатам построения дерева можно реконструировать сценарий эволюции. От гипотетической предковой последовательности сахароизомеризующего домена произошли предковые последовательности дрожжевых и бактериальных доменов. От предковой последовательности бактериальных доменов произошла предковая последовательность сахароизомеризующих доменов Haemophilus influenzae и Escherichia coli и последовательность сахароизомеризующего домена Bacillus subtilis. В свою очередь предковая последовательность дрожжевых доменов дала начало последовательностям сахароизомеризующих доменов Schizosaccharomyces pombe и Candida albicans, а предковая последовательность доменов Haemophilus influenzae и Escherichia coli — последовательностям Haemophilus influenzae и Escherichia coli.
Так как все сахароизомеризующие домены входят в состав ортологичных последовательностей белков, реконструированные деревья можно рассматривать как филогенетические деревья соответствующих организмов (в противном случае эволюционное расстояние между паралогичными последовательностями двух близких организмов А и Б может превышать расстояние между ортологичными последовательностями организма А и более отдаленного от него организма В). Полученные результаты в целом согласуются с систематическим положением организмов. Алгоритм UPGMA позволил правильно разделить их на прокариот и эукариот. В составе прокариот были правильно выделены типы Firmicutes (Bacillus subtilis) и Proteobacteria (Haemophilus influenzae и Escherichia coli). Однако, в отличие от топологии дерева, длины ветвей вызывают сомнения. Если гипотеза молекулярных часов справедлива, и скорость накопления мутаций в различных систематических группах совпадает, то расстояние от точки расхождения организмов (узла дерева) до листьев дерева должно приблизительно соответствовать рангу таксона, на уровне которого эти организмы расходятся. Но, по данным NCBI Taxonomy, Schizosaccharomyces pombe и Candida albicans расходятся на уровне класса (принадледат к типу Ascomycota), а Haemophilus influenzae и Escherichia coli — на уровне порядка (принадлежат к классу Gammaproteobacteria). Тем не менее высоты соответствующих кластеров примерно равны (0.1250 и 0.1150). Кроме того, по результатам реконструкции филогенетического дерева, Bacillus subtilis (тип Firmicutes) отдален от представителей типа Proteobacteria приблизительно настолько, насколько и от эукариотических организмов (0.5876 и 0.6026), что также вызывает сомнения.
Расхождения с устоявшимися представлениями о систематике живых организмов можно объяснить двумя причинами:

малым объемом выборки (134 позиции выравнивания единственного домена);
несовершенством метода UPGMA (например, не учитываются различия в скорости накопления мутаций в последовательностях различных организмов).

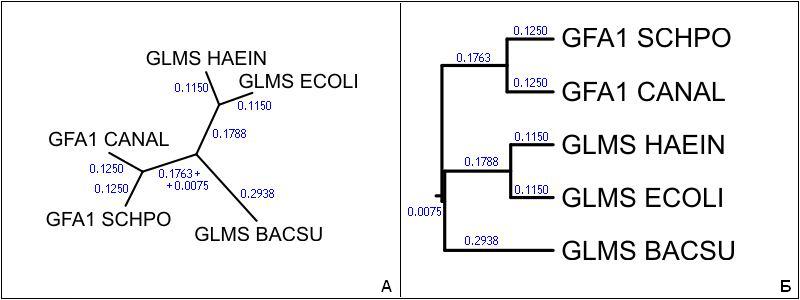
Рис. 2 (А, Б). Визуализация деревьев, построенных по алгоритму UPGMA для фрагментов последовательостей GFA1_SCHPO, GLMS_HAEIN, GLMS_ECOLI, GFA1_CANAL и GLMS_BACSU, соответствующих сахароизомеризующему домену. Синими цифрами показаны длины ветвей. А. Неукорененное дерево, полученное с помощью программы drawtree. Б. Укорененное дерево, полученное с помощью программы drawgram.

Построение дерева по методу ближайших соседей

Построение дерева по методу ближайших соседей (neighbor-joining) было проведено с помощью программы ClustalW. В качестве исходных данных использовались аминокислотные последовательности сахароизомеризующих доменов. Правильная скобочная структура полученного дерева приведена ниже:

((GFA1_SCHPO:0.12155,GFA1_CANAL:0.12657):0.20207,(GLMS_HAEIN:0.12604,GLMS_ECOLI:0.09784):0.14652,GLMS_BACSU:0.28665);
На рис. 3 (А, Б) представлены два варианта визуализации дерева. Неукорененное дерево, полученное с помощью программы drawtree, представлено на рис. 3А. Укорененное дерево, полученное с помощью программы drawgram, представлено на рис. 3Б. Так как правильная скобочная структура, реконструированная по методу ближайших соседей, не содержит информации о корне, наиболее верным является неукорененное дерево. Положение корня в укорененном дереве выбрано случайным образом и не несет осмысленной информации.
Топология деревьев, реконструированных различными методами, совпадает. Следовательно, совпадают и сценарии эволюции. Устойчивость результата подтверждает корректность применения обоих методов.
Как показывает дерево, реконструированное по методу ближайших соседей, скорость накопления мутаций в различных систематических группах различна. Например, последовательность сахароизомеризующего домена Haemophilus influenzae удалена от точки расхождения с последовательностью Escherichia coli на 0.1260, а последовательность Escherichia coli — на 0.0978 (расположение корня дерева между двумя близкородственными организмами представляется маловероятным). Таким образом, в данном случае гипотеза молекулярных часов применима с существенными ограничениями, и дерево, реконструированное по методу ближайших соседей, является более надежным.
Неукорененное дерево (см. рис. 3А) следует рассматривать как множество возможных укоренений. Наиболее вероятным является укоренение на отрезке между про- и эукариотическими организмами (как соответствующее устоявшимся представлениям об эволюции и систематике живых организмов). В этом случае можно оценить скорость накопления мутаций в последовательностях сахароизомеризующих доменов различных организмов. Расстояния от точки расхождения дрожжевых организмов до листьев Schizosaccharomyces pombe и Candida albicans приблизительно равны (0.1266 и 0.1220). Близкие скорости возникновения мутаций в последовательностях этих организмов могут быть обусловлены сходством занимаемых экологических ниш. Расстояния от точки расхождения Firmicutes и Proteobacteria до листьев Haemophilus influenzae, Escherichia coli и Bacillus subtilis соответственно равны 0.2725, 0.2443 и 0.2867. Следовательно, последовательность домена Escherichia coli эволюционирут медленнее последовательностей доменов двух других прокариотических организмов. Такие различия могут быть обусловлены ошибками, возникающими в результате малого объема выборки. Возможно также, что среда обитания Escherichia coli и других представителей порядка Enterobacteriales является более стабильной, чем среды обитания Haemophilus influenzae (порядок Pasteurellales) и Bacillus subtilis (порядок Bacillales), или системы репарации повреждений ДНК у Enterobacteriales развиты лучше.

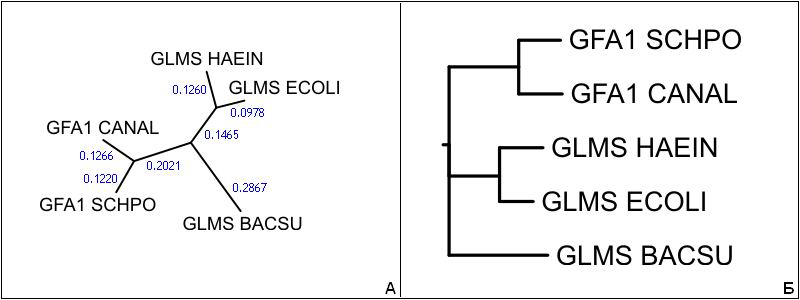
Рис. 3 (А, Б). Визуализация деревьев, построенных по методу ближайших соседей для фрагментов последовательостей GFA1_SCHPO, GLMS_HAEIN, GLMS_ECOLI, GFA1_CANAL и GLMS_BACSU, соответствующих сахароизомеризующему домену. Синими цифрами показаны длины ветвей. А. Неукорененное дерево, полученное с помощью программы drawtree. Б. Укорененное дерево, полученное с помощью программы drawgram.