1. Задание функции

В данном задании было необходимо проанализировать качество восстановления одномерной функции ЭП в зависимости от полноты набора измеренных гармоник и величины экспериментального шума. 
Для начала была смоделирована функция электронной плотности в одномерной элементарной ячейке на отрезке [0,30]. Модель представляла собой две молекулы, расположенные на расстоянии около 5 Å друг от друга. Первая молекула состояла из двух атомов, вторая - из трех. 
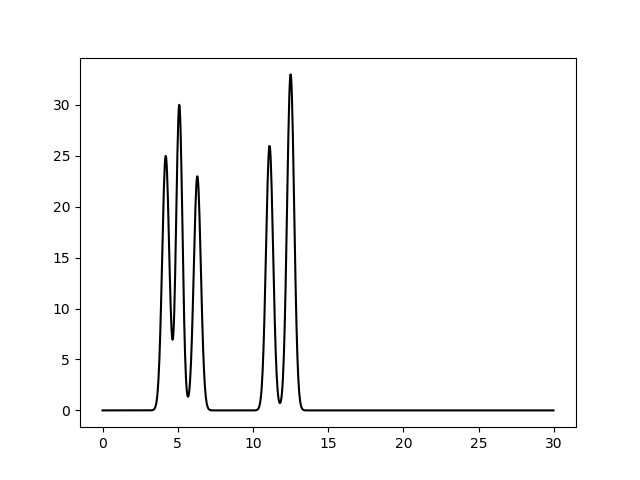
Функция была получена с помощью скрипта compile-func.py (этот скрипт использует дополнительный модуль fourier) с параметрами 30,3.4,5.1+25,3,4.2+23,3,6.3+26,3,11.1+33,3,12.5(сумма пяти гауссовских функций с максимумами в точках 5.1, 4.2, 6.3, 11.1, 12.5 и с величиной пиков 30, 25, 23, 26, 33). График полученной функции представлен на рисунке 1.

Рис. 1. Функция ЭП для одномерной модели.

2. Полные наборы гармоник

На следующем этапе было необходимо разложить полученную функцию в ряд Фурье. Операция производилась с помощью скрипта func2fourier.py. На выходе был получен файл func.txt, содержащий номер гармоники. амплитуду и фазу. Всего в файле 499 гармоник. Далее было найдено минимальное число гармоник, по которым можно достаточно точно восстановить исходную функцию ЭП. Для восстановления функции электронной плотности по набору гармоник был использован скрипт fourier2func.py, а для отбора необходимых гармоник из полного набора - скрипт fourier-filter.py. 
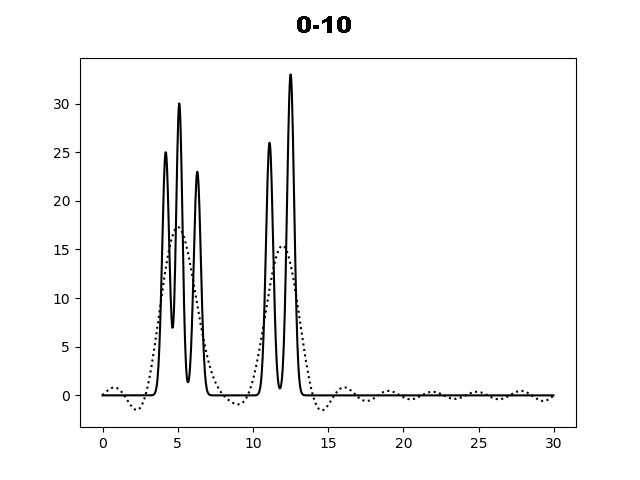
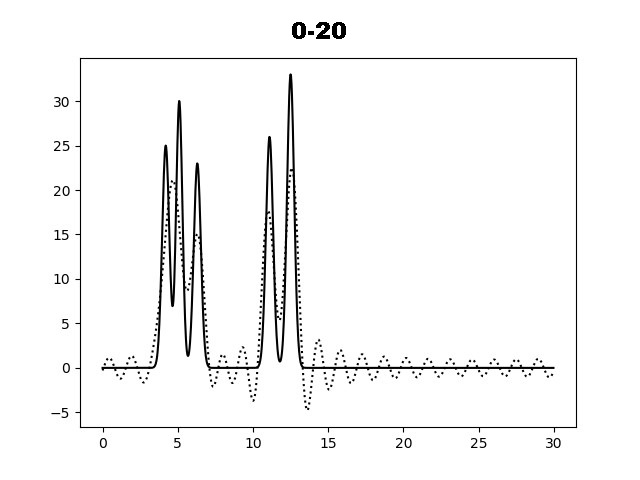
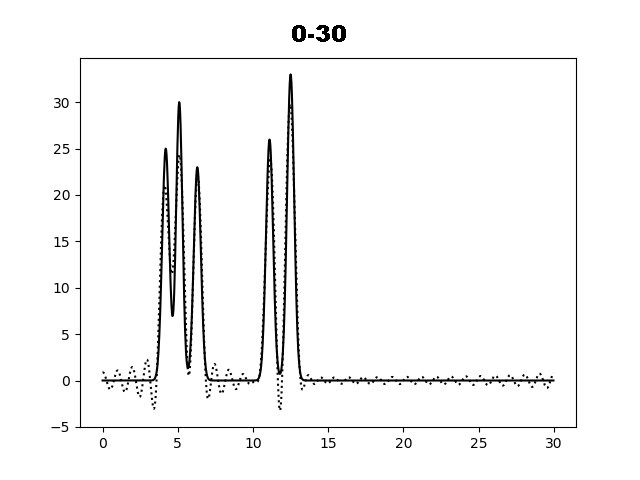
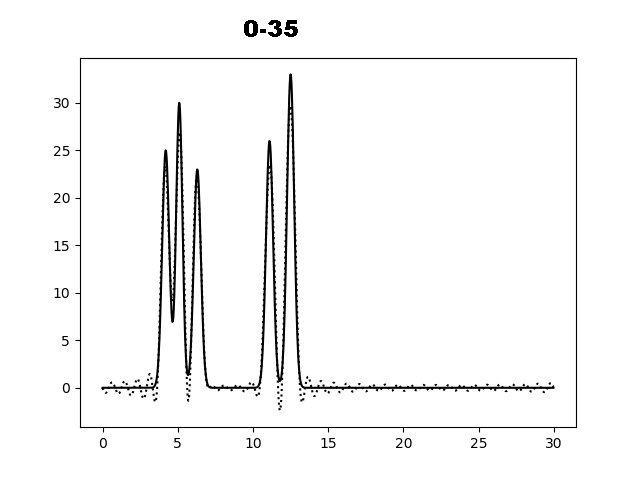
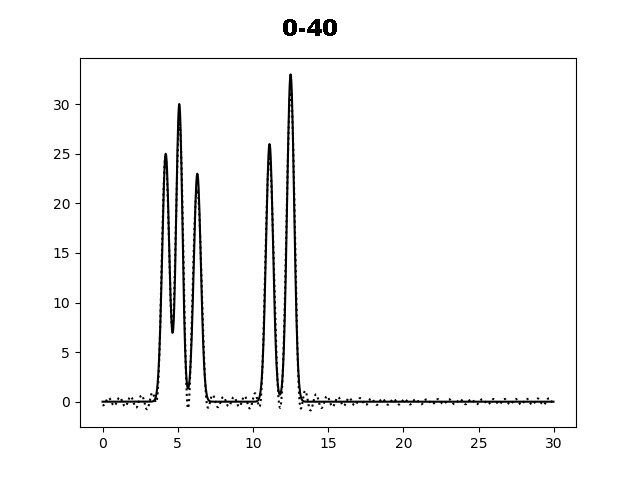
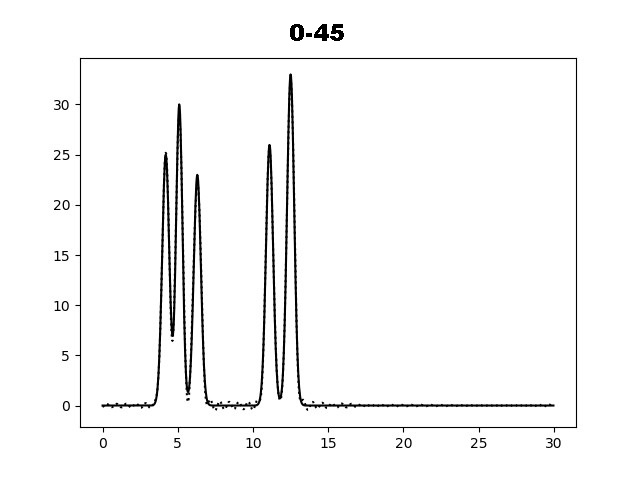
На рисунке 2 показаны графики функций электронной плотности, восстановленные по первым 10, 20, 30, 35, 40 и 45 гармоникам разложения. По графику функции для набора гармоник 0-35 можно определить положение максимума всех слагаемых функции и охарактеризовать как "отличное восстановление". Далее вся работа проводилась с набором гармоник 0-40.

Рис. 2. Восстановление функции ЭП по первым гармоникам.

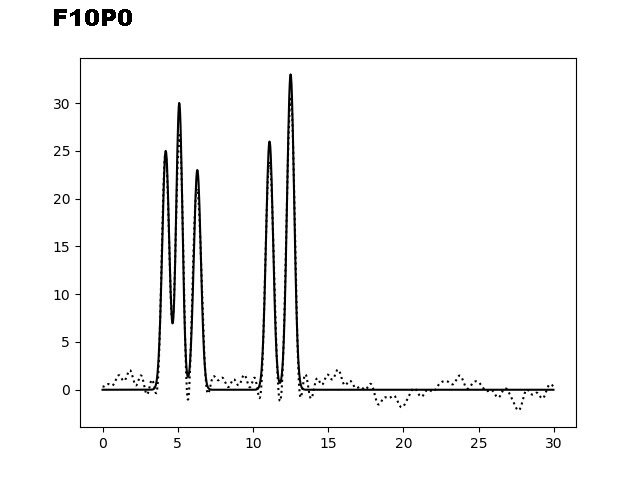
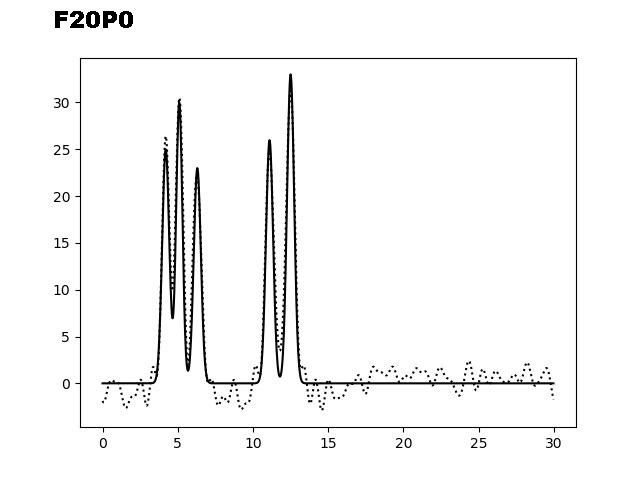
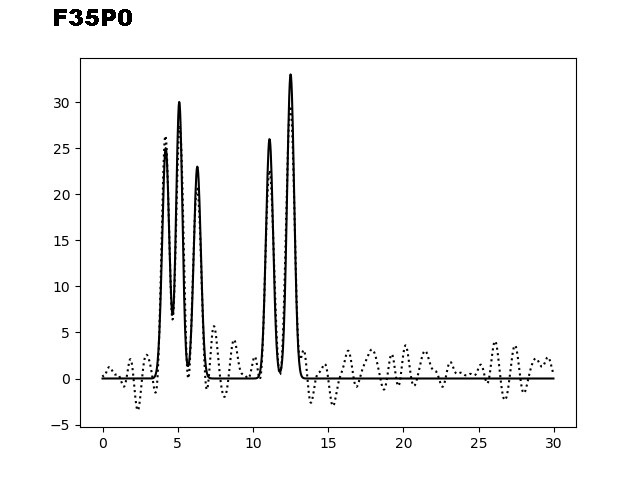
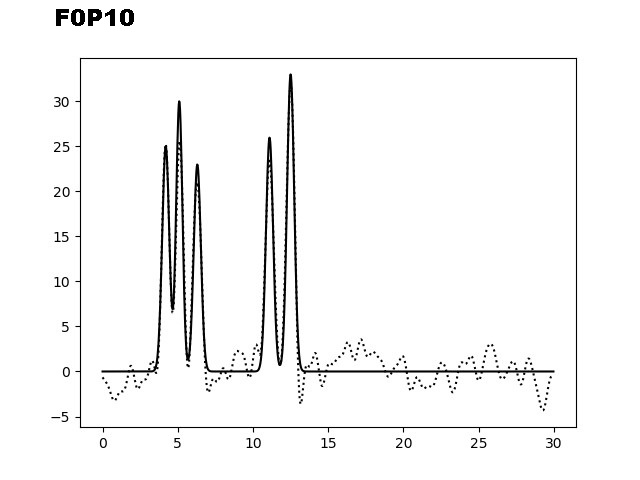
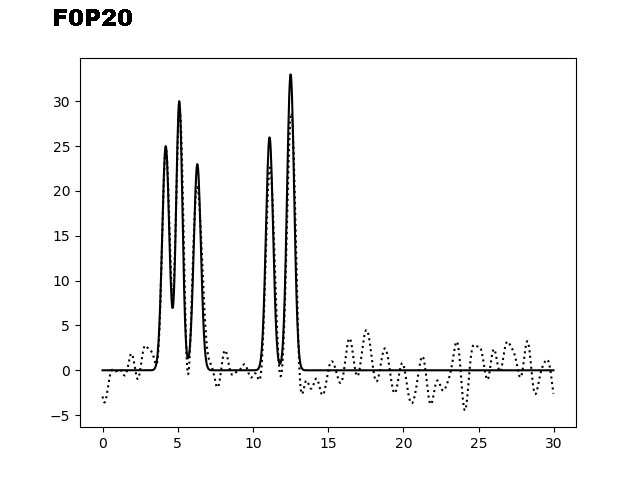
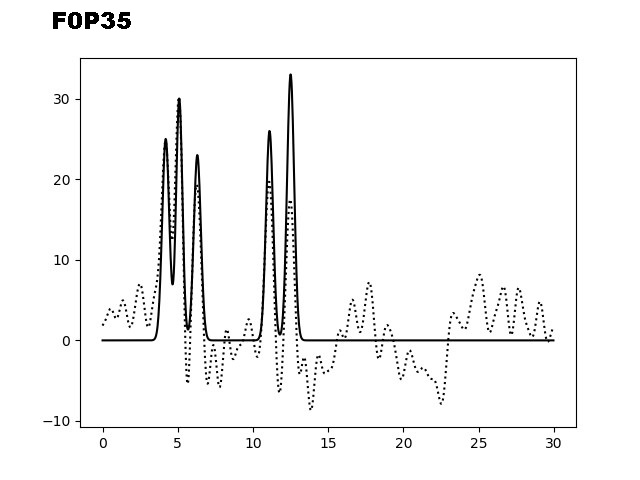
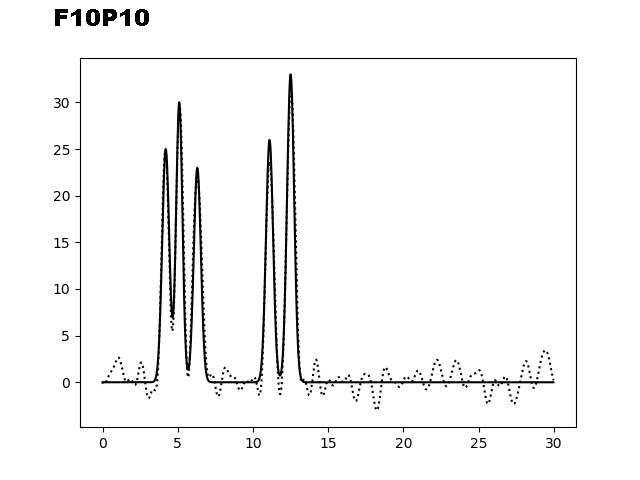
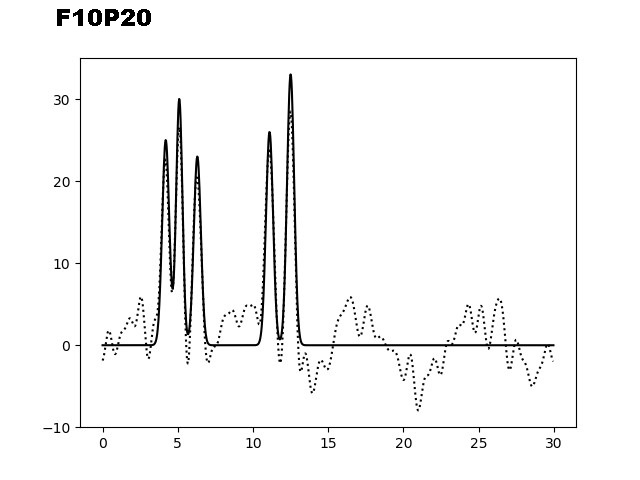
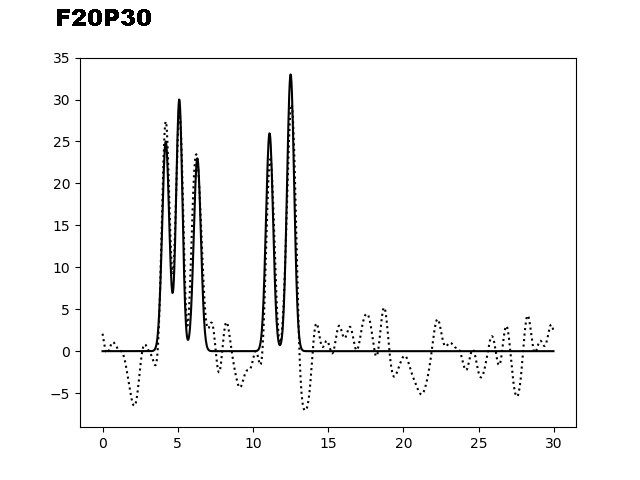
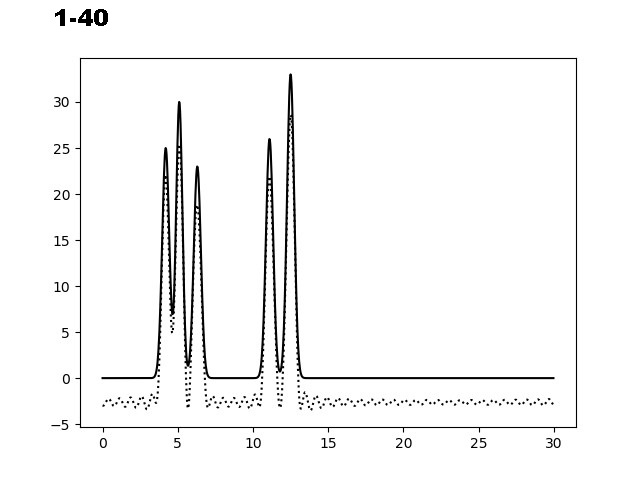
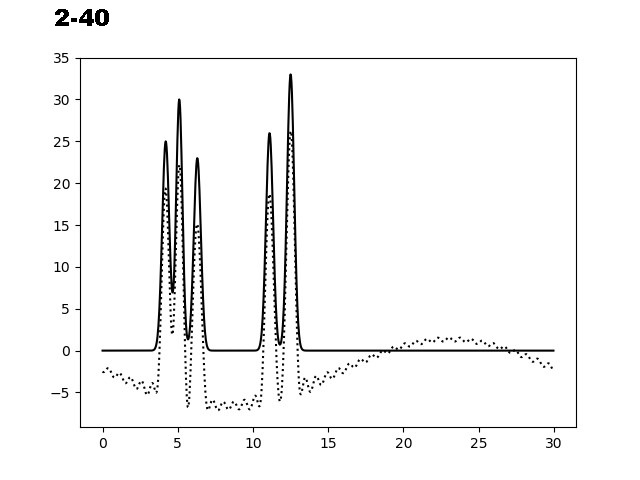
На следующем этапе было необходимо изучить восстановление ЭП при добавлении шума (к фазам (P) и/или к амплитудам (F)). На рисунке 3 представлены графики электронной плотности, восстановленные по первым 40 гармоникам с добавлением шума к амплитудам (10, 20 и 35), к фазам (10, 20 и 35) и одновременно к обоим параметрам (10/10, 10/20 и 20/30).

Рис. 3. Добавление шума к фазам (Р) и/или амплитудам (F) для набора гармоник 0-40.

Из графиков, представленных на рисунке 3, можно заметить, что добавление 10% шума одновременно к фазам и амплитудам не искажает сильно восстановление функции ЭП. Важно отметить, что при добавлении 35% шума только к фазам, уже не позволяет угадать положение максимумов гауссовых функции, в отличие от случая, когда мы добавляем те же 35% шума к и/или амплитудам. Восстановление функции по отобранным гармоникам было производилось скриптом fourier2func.py.

3. Неполные наборы гармоник

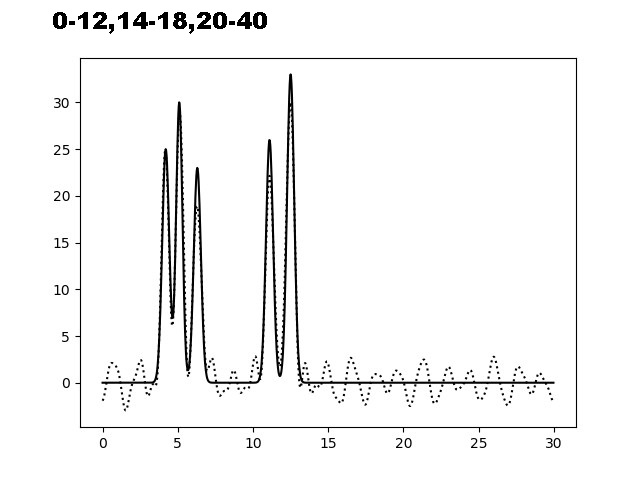
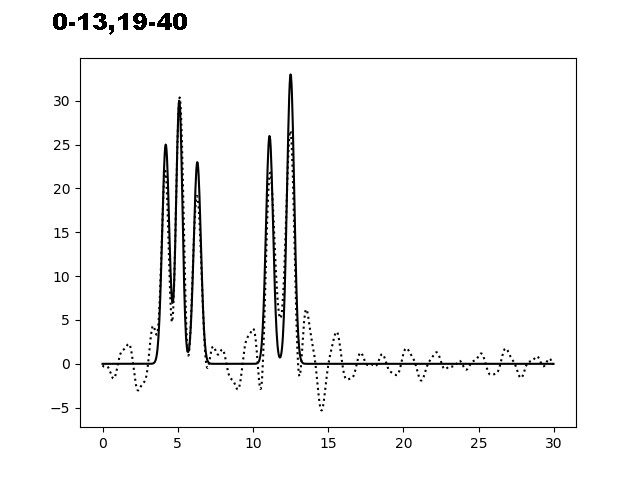
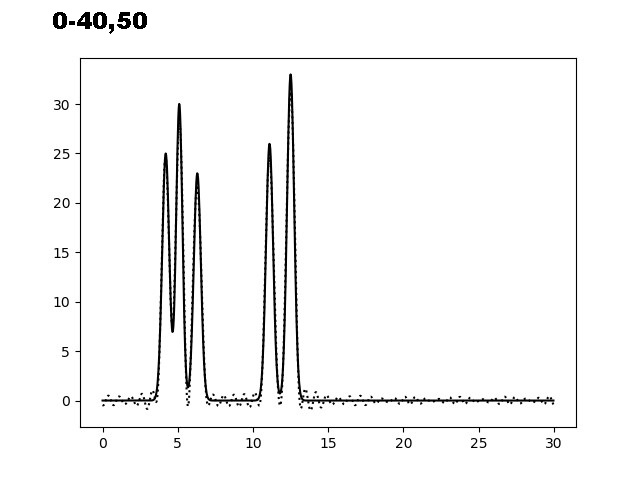
Для получения неполного набора гармоник были удалены одна и две начальные гармоники (гармоника с номером 0; гармоники с номерами 0 и 1).Также были удалены гармоники из середины множества (подмножества 0-12,14-18,20-40; 0-13,19-40), а также было взято 40 гармоник с добавлением еще одной гармоники под номером 50.Результаты отображены на рисунке 4.

Рис. 4. Восстановление неполного набора гармоник и набора гармоник с добавлением еще одной.

Удаление 5% гармоник из середины (подмножество 0-12,14-18,20-40) не приводит к сильному искажению восстановления функции ЭП, в отличие от случая, когда из середины удаляются 12,5% гармоник (подмножество 0-13,19-40), где отдельные атомы уже не могут быть определены однозначно. Удаление первой гармоники приводит к сдвигу оси ОУ, но не влияет на вид восстановленной функции ЭП. Добавление в конец еще одной гармоники как видно не влияет сильно на качество восстановления. 

Набор гармоник

Разрешение

(Å)

Полнота данных

(%)
Шум амплитуды (% от величины F)

Шум фазы

(% от величины phi)

Качество восстановления
Полный набор гармоник
0-10
3
100
0
0
Плохое
0-30
1
100
0
0
Хорошее
0-40
0,75
100
0
0
Отличное
0-40
0,75
100
35
0
Хорошее
0-40
0,75
100
0
35
Среднее
0-40
0,75
100
10
20
Среднее
Неполный набор гармоник
1-40
0,75
97,5
0
0
Отличное
2-40
0,75
95
0
0
Отличное
0-12,14-18,20-40
0,75
95
0
0
Хорошее
0-13,19-40
0,75
87,5
0
0
Среднее
0-40,50
0,75
100
0
0
Отличное

Для оценки качества восстановления исходной функции использовались следующие критерии:

Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")

Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума

Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно

Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"