Множественное выравнивание последовательностей белков
Сравнение выравниваний одних и тех же последовательностей разными программами
Для этого задания я выбрала белки с мнемоникой из 9 практикума: DNLJ. Были выбраны 5 белков: DNLJ_ECOLI, DNLJ_HALVD, DNLJ_MYCTU, DNLJ_THEFI и DNLJ_MYCS2. Были получены выравнивания в Jalview с помощью команд Muscle и Mafft
Ссылка на выравнивание с помощью Muscle
Ссылка на выравнивание с помощью Mafft
Затем я сравнила выравнивания с помощью программы Артема Тюкаева, Якова Коробицына, Матвея Киселева и Георгия Малахова. Результат выдачи программы:
| F1-L1 | F2-L2 |
|---|---|
| 1-3 | 1-3 |
| 39-95 | 42-98 |
| 99-131 | 102-134 |
| 141-253 | 144-256 |
| 280-421 | 284-425 |
| 438-449 | 442-453 |
| 454-521 | 458-525 |
| 541-633 | 545-637 |
| 649-731 | 657-739 |
Видно, что имеется достаточно много совпадающих блоков, они идут часто и несильно сдвинуты друг относительно друга. Это говорит о том, что программы работают довольно слаженно. Также такой результат связан с тем, что все белки несильно отличатся по длине и имеют много консервативных участков.
Построение выравнивания по совмещению структур и сравнение его с выравниванием MSA
Было выбрано 3 белка изсемейства BRCT (ID PF00533): DNLJ_ECOLI, DNLJ_BORRA и DNLJ_DESPS. С помощью инструмента align было получено выравнивание в PyMOL.
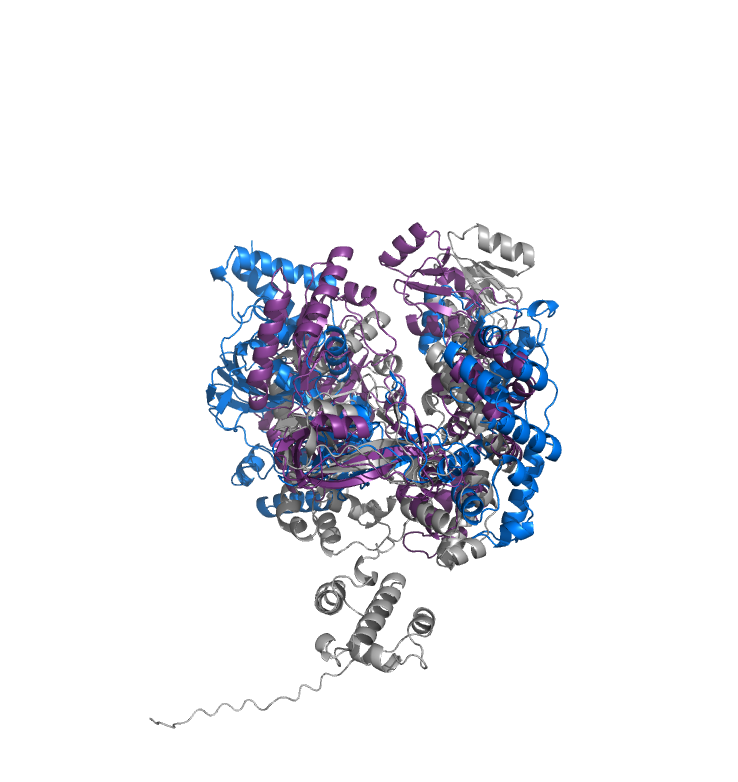
Также было получено выравнивание в Jalview с помощью Muscle. Выравнивания в Jalview и PyMOL совпадают, так как наблюдаются консервативные участки в середине и на N-конце, а на С-конце у DNLJ_DESPS остаётся длинный хвост.
Краткое описание Muscle
MUSCLE (MUltiple Sequence Comparison by Log-Expectation) – программа для множественного выравнивания аминокислотных и нуклеотидных последовательностей. Впервые метод был опубликован Робертом С. Эдгаром в 2004 году.
Алгоритм MUSCLE состоит из трех этапов: предварительный прогрессивный , улучшенный прогрессивный и этап уточнения.
Этап 1. На этом первом этапе алгоритм производит множественное выравнивание, делая упор на скорость, а не на точность. Этот шаг начинается с вычисления расстояния k-меров для каждой пары входных последовательностей, чтобы создать матрицу расстояний. На её основе для созданиётся бинарное дерево. Из этого дерева строится прогрессивное выравнивание, начиная с "листьев" дерева. Это продолжается до тех пор, пока не получится множественное выравнивание всех входных последовательностей в "корне" дерева.
Этап 2. На этом этапе основное внимание уделяется получению более оптимального дерева. Повторяются действия первого этапа, но вместо k-меров используются расстояния Кимуры, которые являются более точными. На основании новой матрицы аналогично 1 этапу строятся выравнивания, но только в поддеревьях, порядок ветвления которых изменился по сравнению с первым деревом.
Этап 3. На этом заключительном этапе из второго дерева выбирается ребро (в порядке приближения к корню). Выбранное ребро удаляется, разделяя дерево на два поддерева. Затем для каждого поддерева вычисляется профиль множественного выравнивания. Новое выравнивание производится путем повторного выравнивания профилей поддерева. Если оценка SP (sum of pair) улучшается, новое выравнивание сохраняется, в противном случае оно отбрасывается. Процесс повторяется до схождения или до достижения заданного пользователем предела.