Восстановление функции по коэффициентам её ряда Фурье

Задание функции

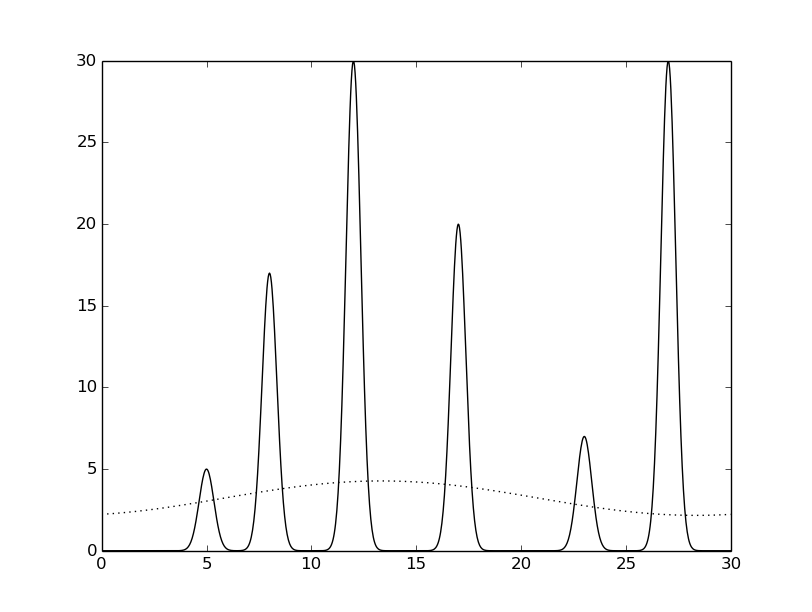
Модель для компьютерного эксперимента: шесть атомов расположены на расстоянии около 5 Å на отрезке [0, 30]. Электронные плотности атомов описываются гауссовой кривой. Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py

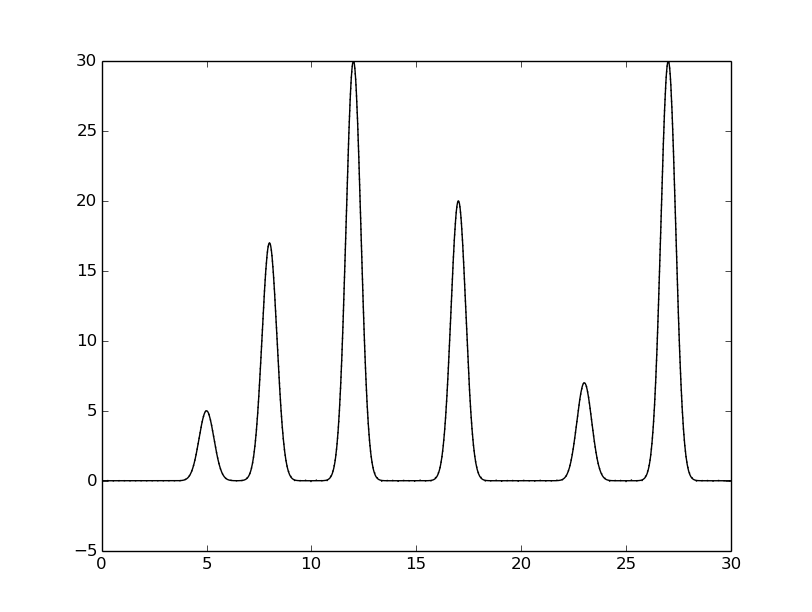
python compile-func.py -g 5,2,5+17,2,8+30.0,2,12+20.0,2,17+7.0,2,23+30,2,27

Выходной файл скрипта - текстовый файл func.txt, в котором описана заданная функция. С помощью скрипта было получено изображение заданной функции (рисунок 1).

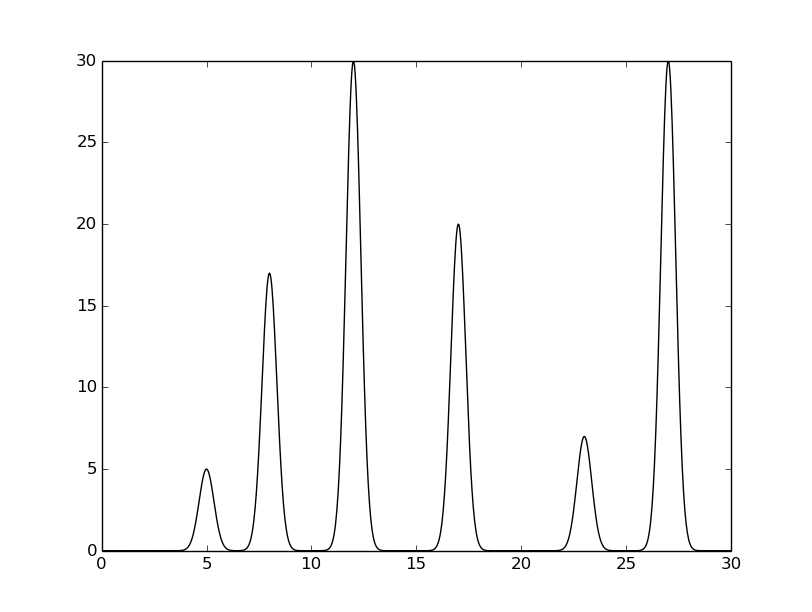
Рисунок 1. График заданной функции.

Полные наборы гармоник

Расчет коэффициентов Фурье

Коэффициенты разложения заданной функции в ряд Фурье были получены с помощью скрипта func2fourier.py.

python func2fourier.py -i func.txt

Выходной файл func_ft.txt содержит номера, амплитуды и фазы гармоник.

Отбор гармоник и восстановление функций

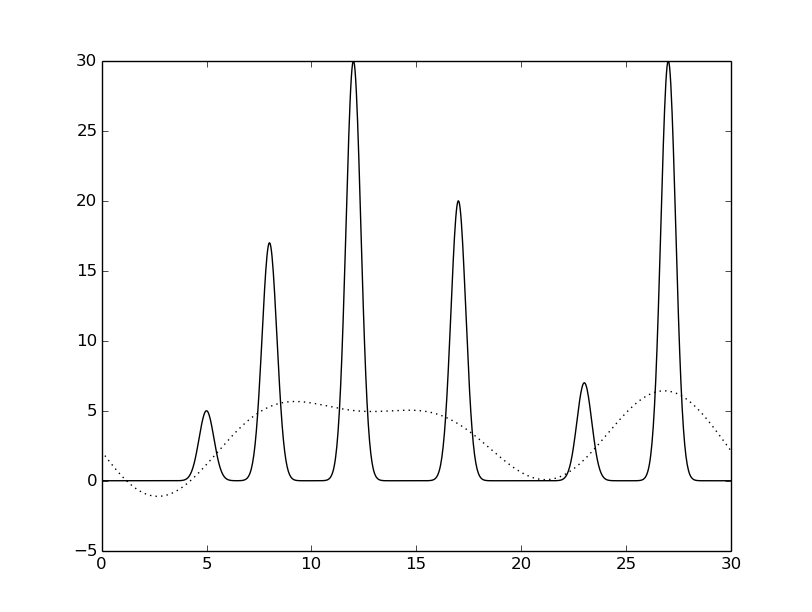
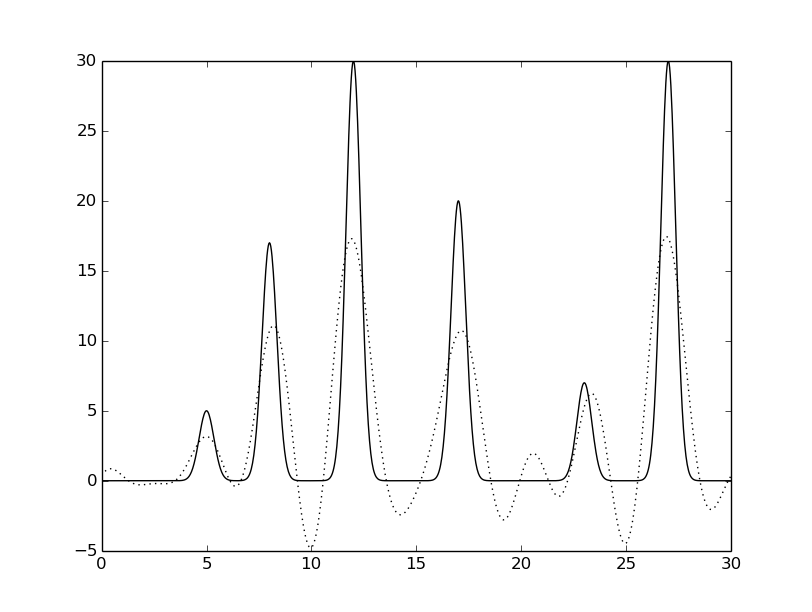
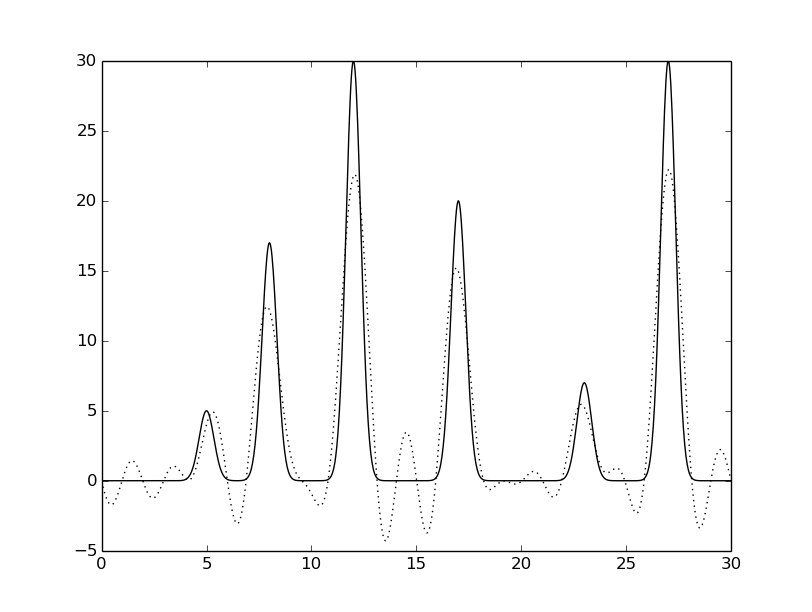
Всего было получено 499 гармоник. Необходимо найти n0, для которого по графику функции, восстановленной по набору гармоник 0, 1, ..., n0 можно определить положение максимумов всех гауссовых слагаемых («отличное восстановление»).

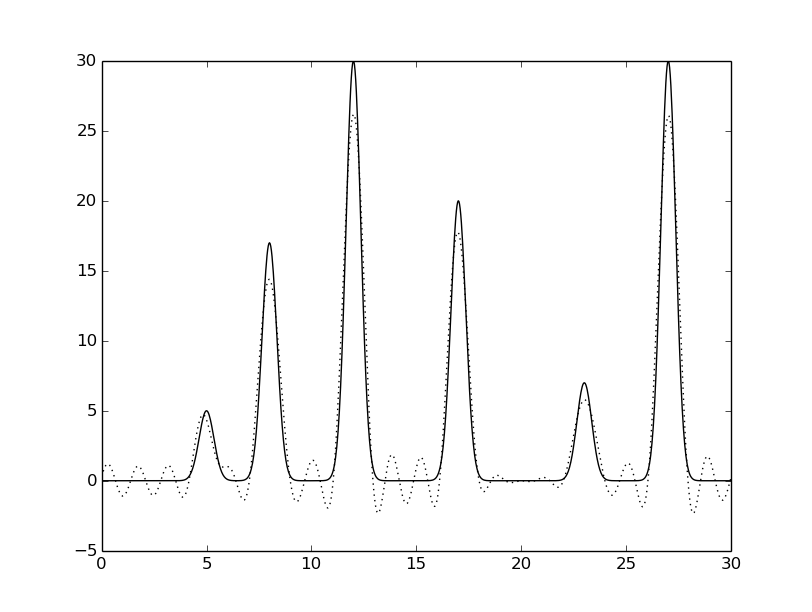
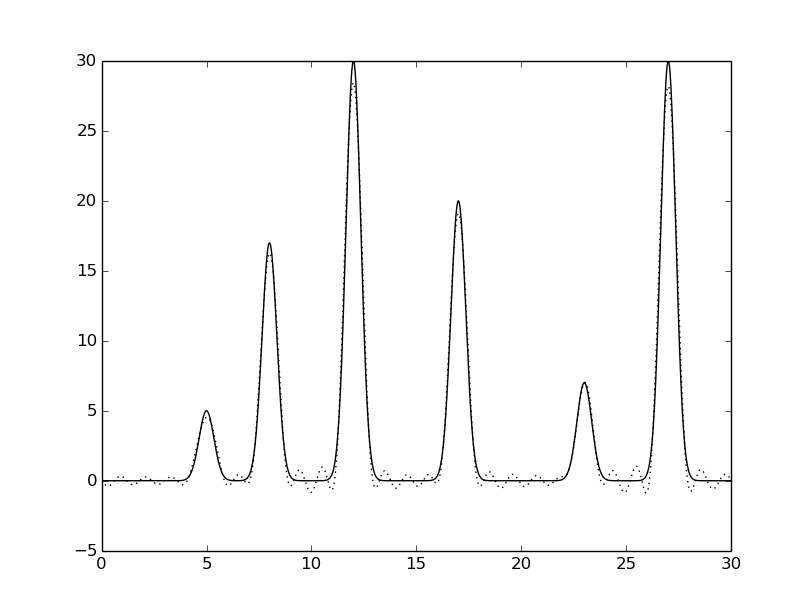
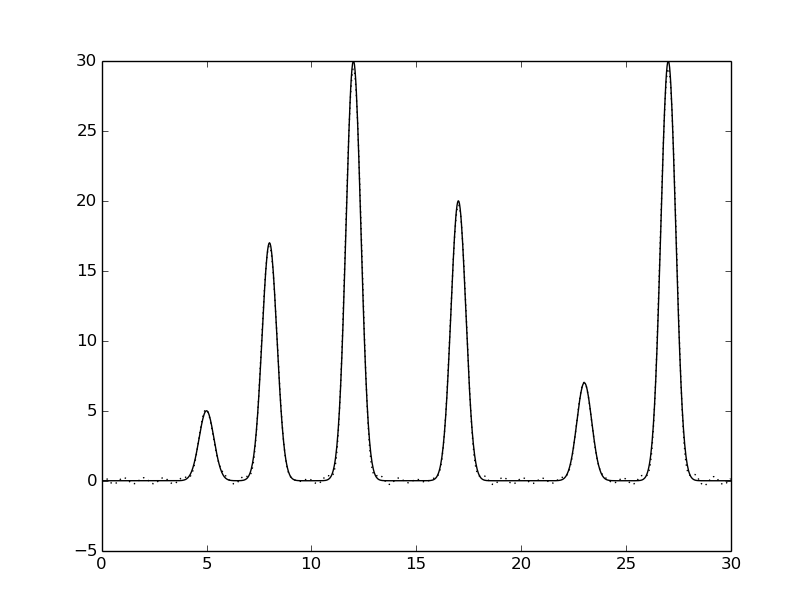
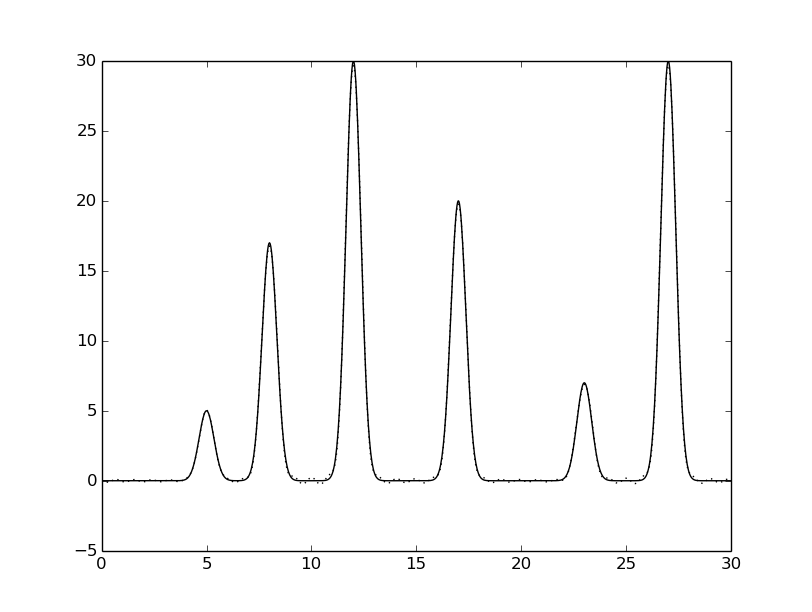
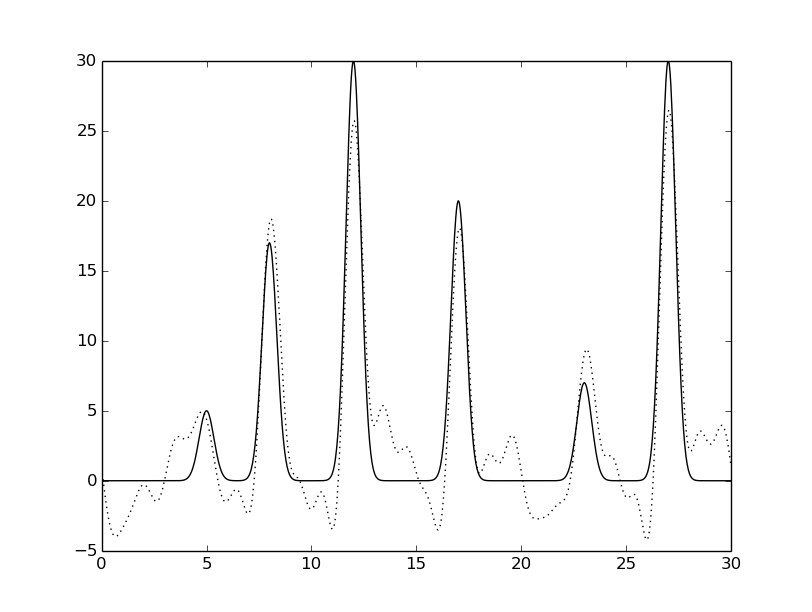
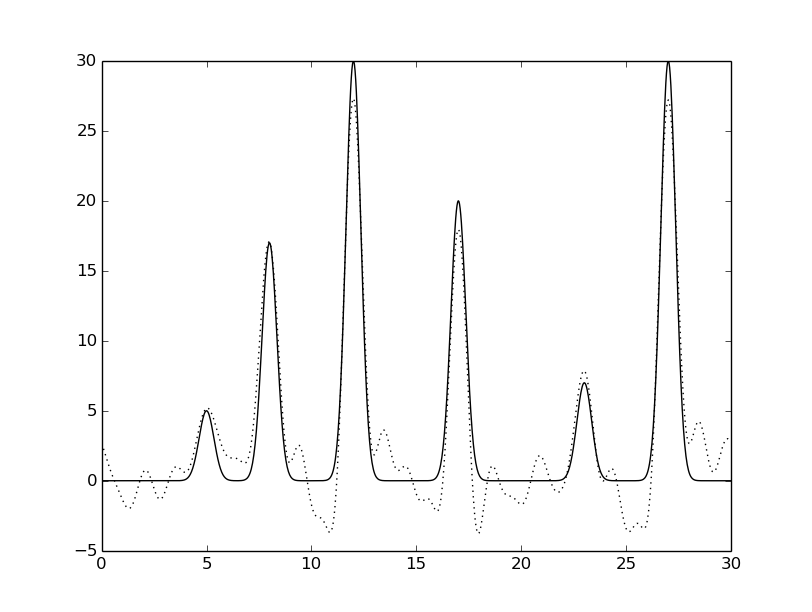
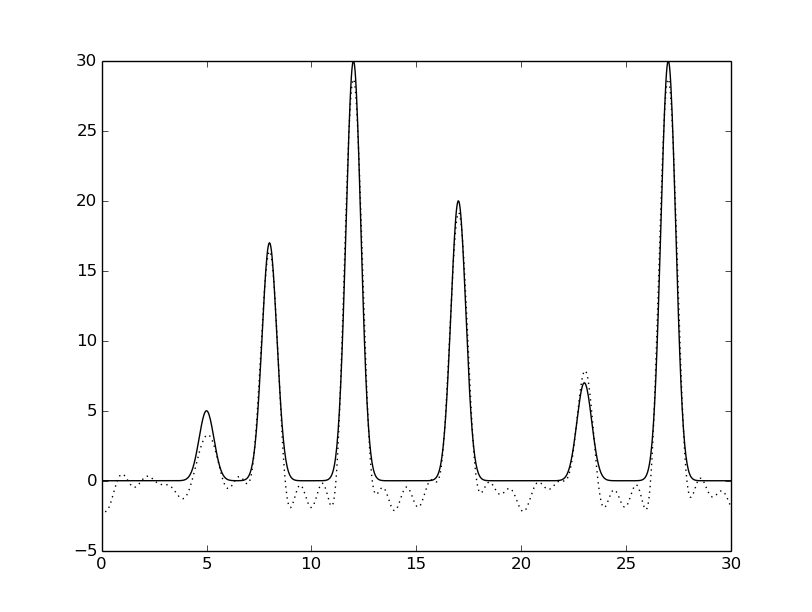
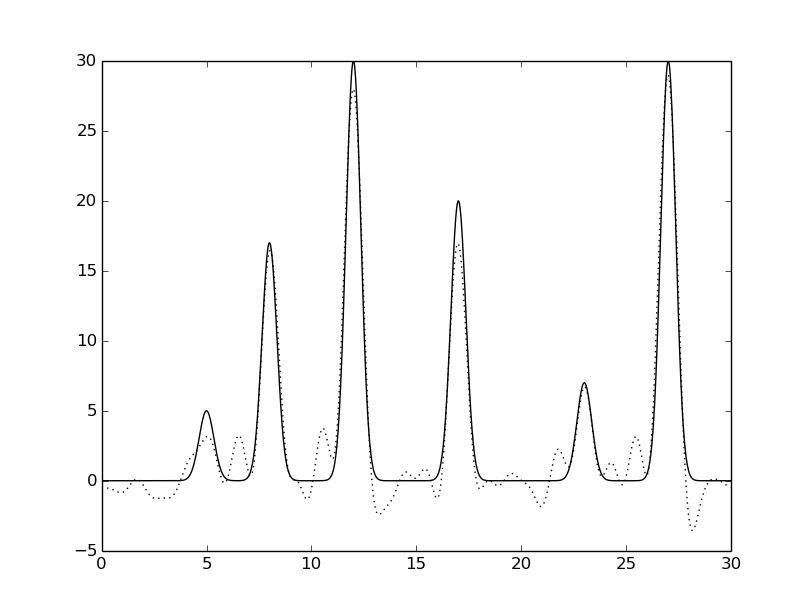
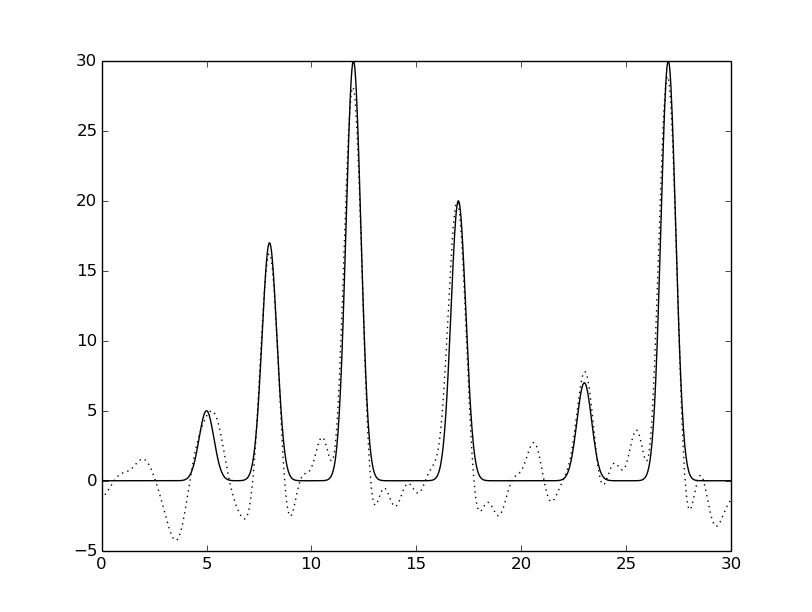
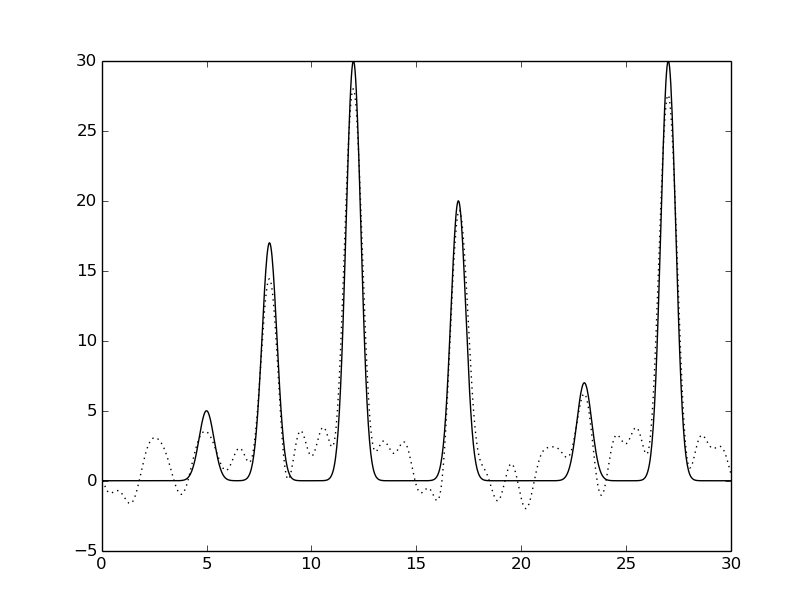
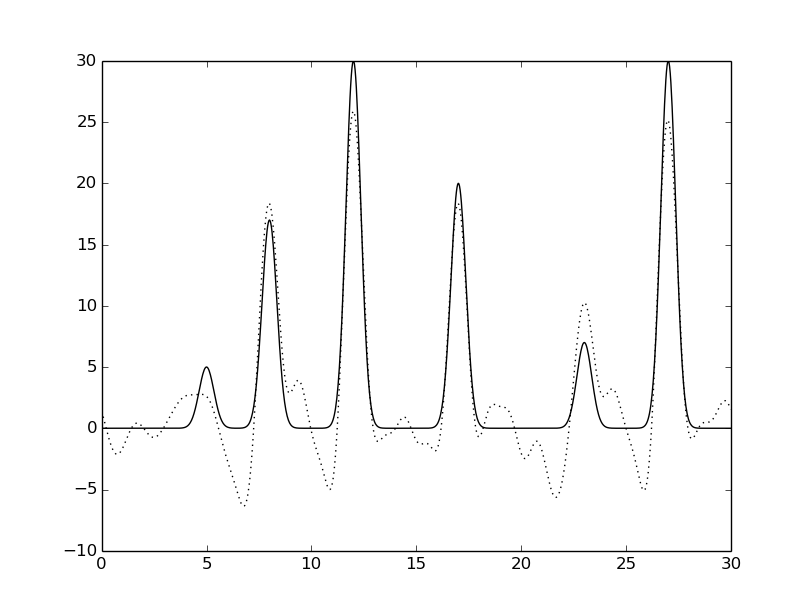
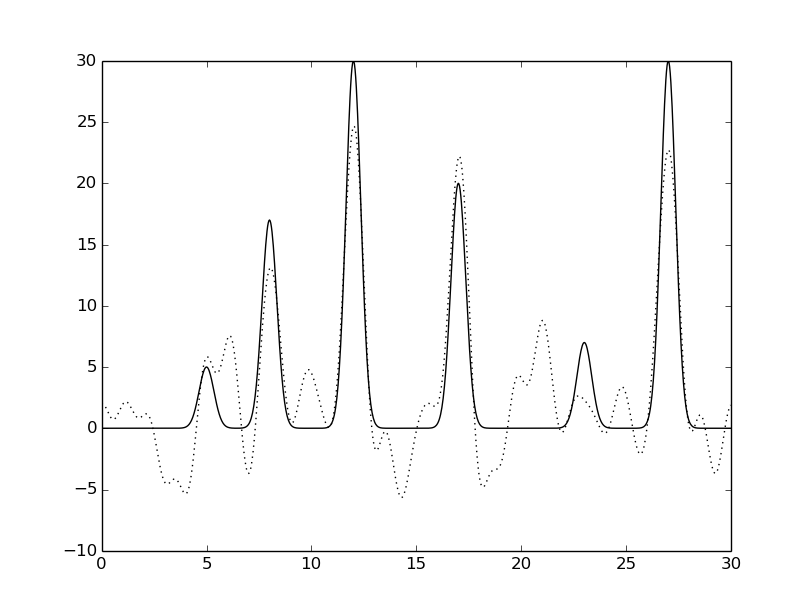
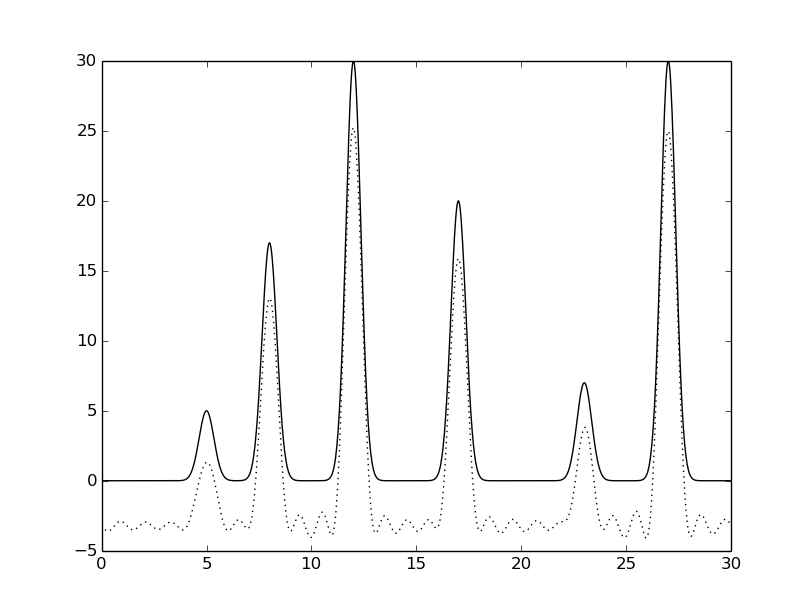
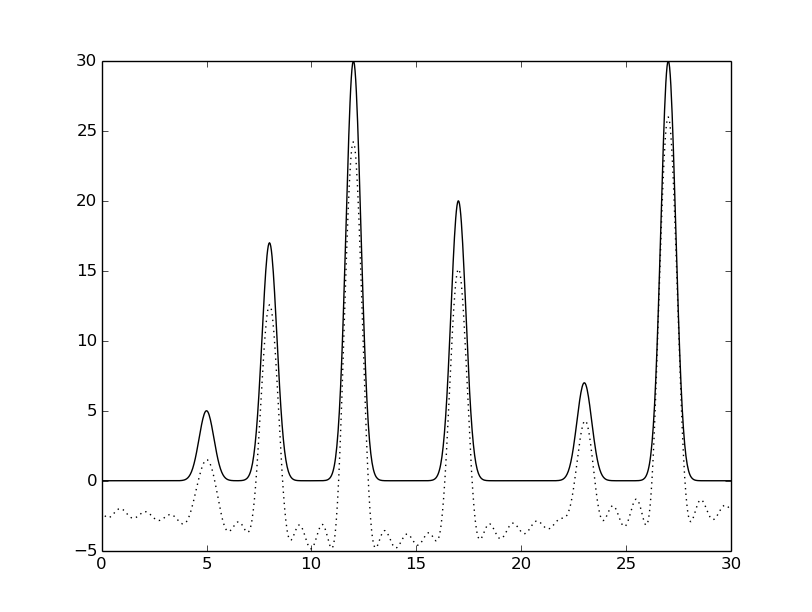
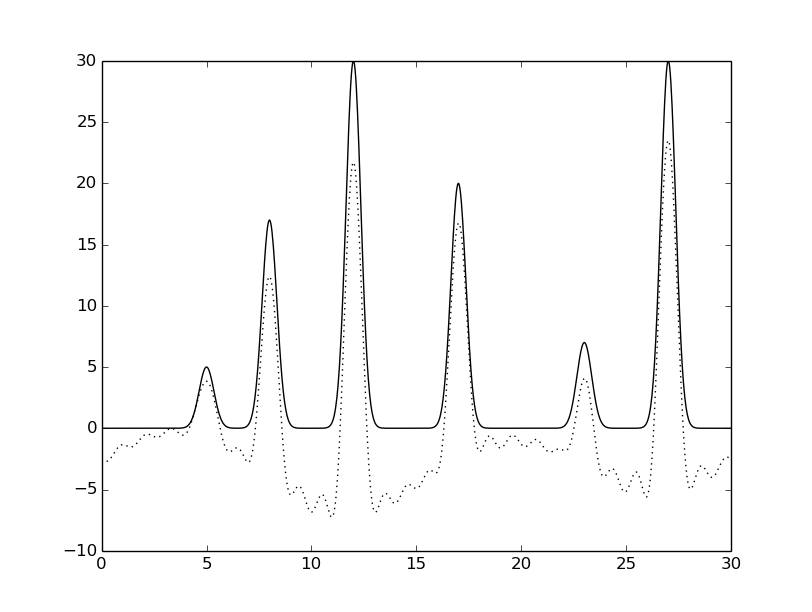
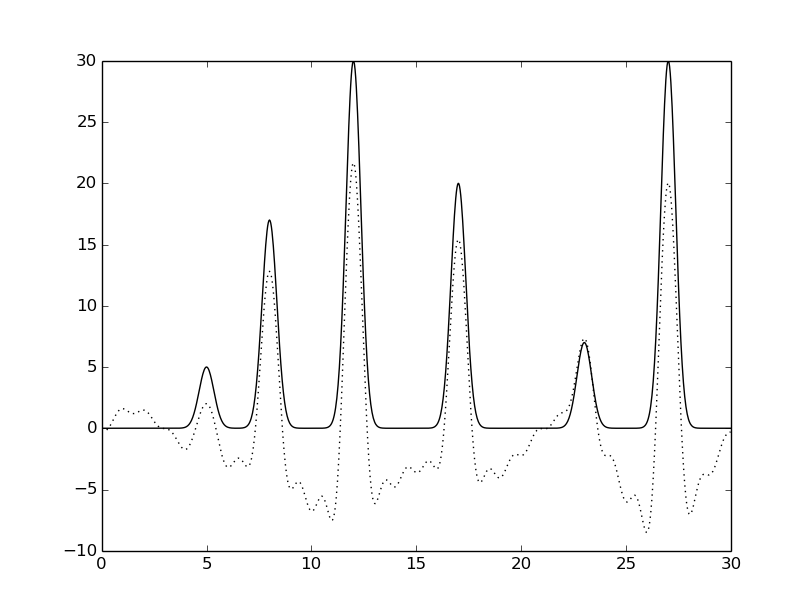
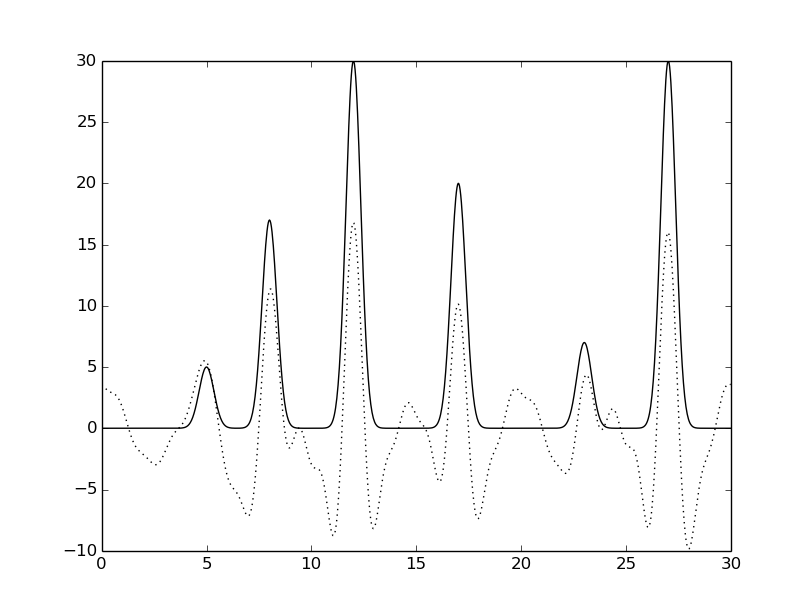
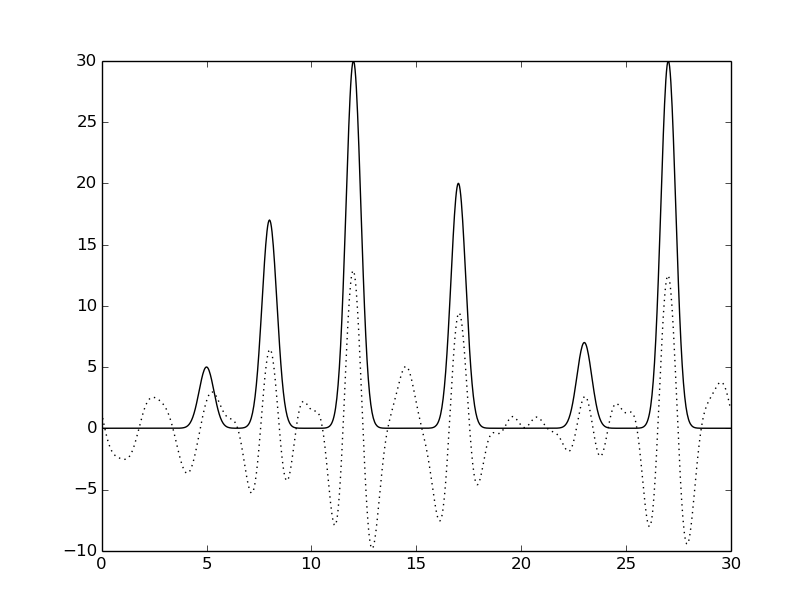
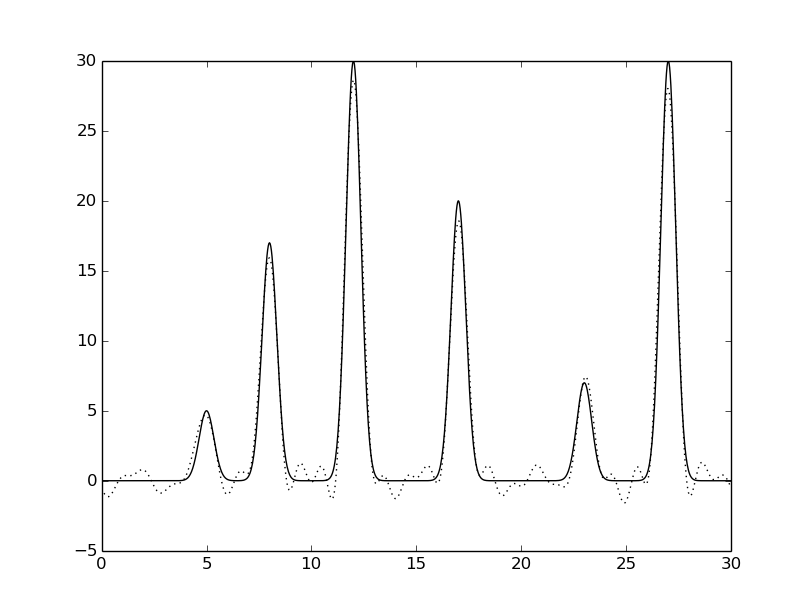
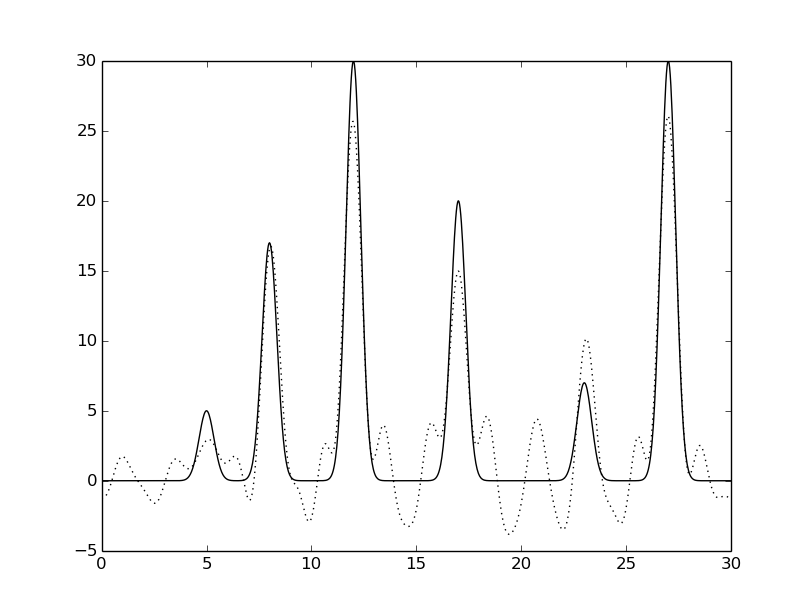
python fourier-filter.py -r 0-* -i func_ft.txt -o func_ft_0-*.txt
python fourier2func.py -f func.txt -i func_ft_0-*.txt -o two_func_0-*.txt

На рисунках 2-10 представлены графики восстановленных функций по полным наборам гармоник для различных n (крупные картинки доступны по щелчку, пунктирной линией указана восстановленная функция, сплошной - исходная).

Рисунок 2. n=1.	Рисунок 3. n=3.	Рисунок 4. n=10.
Рисунок 5. n=15.	Рисунок 6. n=20.	Рисунок 7. n=25.
Рисунок 8. n=30.	Рисунок 9. n=35.	Рисунок 10. n=40.

На основании полученных рисунков значение n0 было определено равным 25, так как уже при этом значении можно определить все пики на графике восстановленной функции. При увеличении n востановленная функция приближается к исходной, и уже при n=40 они полностью сливаются.

Добавление шума

Далее к амплитудам и фазам был добавлен шум (0, 10 или 20%) при n0=25:

python func2fourier.py -F * -P * -i func.txt -o ft_noise*-*.txt
python fourier-filter.py -r 0-25 -i ft_noise*-*.txt -o ft_noise*-*_n0.txt
python fourier2func.py -i ft_noise*-*_n0.txt -o two_func_noise*-*_n0.txt

На рисунках 11-18 представлены полученные графики (крупные картинки доступны по щелчку, пунктирной линией указана восстановленная функция, сплошной - исходная).

Рисунок 7. n=25, шума нет.	Рисунок 11. Шум -P 10.	Рисунок 12. Шум -P 20.
Рисунок 13. Шум -F 10.	Рисунок 14. Шум -F 10 -P 10.	Рисунок 15. Шум -F 10 -P 20.
Рисунок 16. Шум -F 20.	Рисунок 17. Шум -F 20 -P 10.	Рисунок 18. Шум -F 20 -P 20.

Из данных рисунков видно, что внесение шума к фазе намного сильнее ухудшает восстановление, чем внесение шума к амплитуде. Однако, во всех случаях сохраняются пики, соответсвтующие тяжелым атомам.

Неполные наборы гармоник

Удаление начальных гармоник

Для получения неполного набора гармоник было удалено несколько начальных гармоник:

python fourier-filter.py -r *-35 -i func_ft.txt -o ft_*-35.txt
python fourier2func.py -i ft_*-35.txt -o two_func_*-35.txt

Полученные графики функций представлены на рисунках 19-24 (крупные картинки доступны по щелчку, пунктирной линией указана восстановленная функция, сплошной - исходная).

Рисунок 19. Удаление первой гармоники (n=0).	Рисунок 20. Удаление гармоник n=0 и n=1.
Рисунок 21. Удаление первых трех гармоник.	Рисунок 22. Удаление первых пяти гармоник.
Рисунок 23. Удаление первых семи гармоник.	Рисунок 24. Удаление первых десяти гармоник.

В случае удаления первой гармоники восстановленная функция смещена по оси ординат, при этом результат восстановления отличный. Это ожидаемый результат, так как значение первой гармоники равно числу F0 – первому коэффициенту ряда Фурье. При удалении следующих гармоник функция значительно искажается, однако видно, что даже при удалении первых семи гармоник значения практически всех пиков можно определить.

Удаление гармоник из середины набора

Далее проводилось удаление гармоник из середины набора:

python fourier-filter.py -r 0-*,*-25 -i func_ft.txt -o ft_0-*_*-25.txt
python fourier2func.py -i ft_0-*_*-25.txt -o two_func_0-*_*-35.txt

Полученные графики функций представлены на рисунках 25, 26 (крупные картинки доступны по щелчку, пунктирной линией указана восстановленная функция, сплошной - исходная).

Рисунок 25. Удаление тринадцатой гармоники (n=12).

Рисунок 26. Удаление гармоник n=10, n=11 и =12.

Удаление 4% гармоник ухудшило качество востановленной функции, однако по ней все равно однозначно можно восстановить все пики, и качество восстановления является отличным. Удаление 12% гармоник привело к искажению восстановленной функции, и уже не все пики можно определить однозначно, так как легкие атомы становятся неотличимы от шума. В данном случае восстановление среднее.

Добавление гармоники n0+10

К набору гармоник 0, 1, ..., 25 была добавлена гармоника 35:

python fourier-filter.py -r 0-25,35 -i func_ft.txt -o ft_0-25_35.txt
python fourier2func.py -i ft_0-25_35.txt -o two_func_0-25_35.txt

Добавление гармоники с номером n0+10 к набору гармоник 0, 1, ..., n0, не изменила качество восстановления:

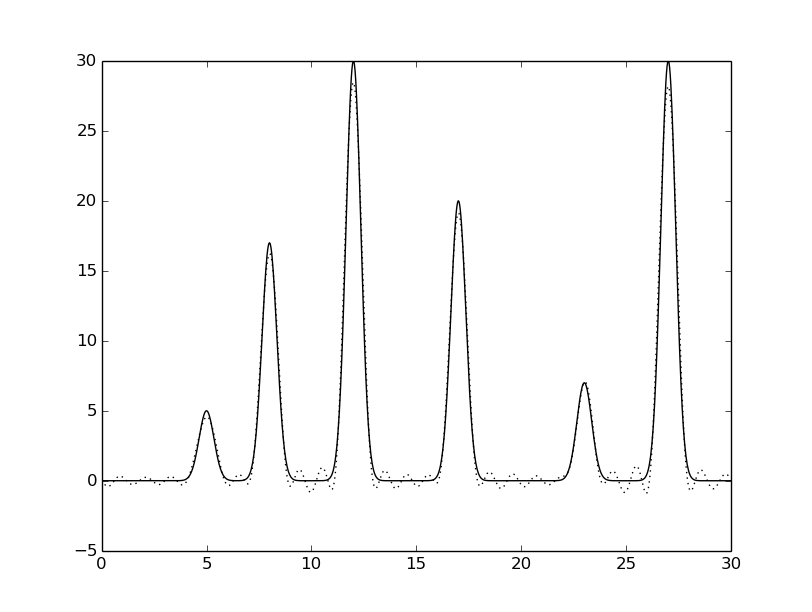
Рисунок 27. Добавление гармоники n0+10.

Определение разрешения и полноты данных

Для полного набора гармоник разрешение - период гармоники с наибольшим номером. Для набора гармоник 0-25 разрешение равно 30 Å/25 = 1.2 Å. Полнота данных - это процент гармоник в наборе, период которых не меньше разрешения, от числа гармоник в полном наборе для этого разрешения. Для полного набора полнота данных равна 100%.

Таблица 1. Восстановление функции по коэффициентам ряда Фурье.
Набор гармоник	Разрешение ( Å)	Полнота данных (%)	Шум амплитуды (% от F)	Шум фазы (% от P)	Качество восстановления
Полный набор гармоник
0-1	30	100	0	0	Плохое
0-3	10	100	0	0	Плохое
0-10	3	100	0	0	Хорошее
0-15	2	100	0	0	Хорошее
0-20	1.5	100	0	0	Хорошее
0-25	1.2	100	0	0	Отличное
0-30	1	100	0	0	Отличное
0-35	0.86	100	0	0	Отличное
0-40	0.75	100	0	0	Отличное
0-25	1.2	100	0	10	Среднее
0-25	1.2	100	0	20	Хорошее
0-25	1.2	100	10	0	Отличное
0-25	1.2	100	10	10	Среднее
0-25	1.2	100	10	20	Хорошее
0-25	1.2	100	20	0	Среднее
0-25	1.2	100	20	10	Среднее
0-25	1.2	100	20	20	Среднее
Неполный набор гармоник
1-25	1.2	0.96	0	0	Отличное
2-25	1.2	0.92	0	0	Отличное
3-25	1.2	0.88	0	0	Отличное
5-25	1.2	0.81	0	0	Среднее
7-25	1.2	0.73	0	0	Среднее
10-25	1.2	0.62	0	0	Среднее
0-12,14-25	1.2	0.96	0	0	Отличное
0-10,14-25	1.2	0.88	0	0	Среднее
0-25, 35	1.2	100	0	0	Отличное

Восстановление функции по коэффициентам её ряда Фурье.