Изучение работы методов контроля температуры в GROMACS.

В процессе выполнения этого задания мы будем изучать, как реализован контроль температуры в молекулярной динамике на примере GROMACS. Объект исследования - одна молекула этана.

1. Подготовка файлов.

Сначала подготовим файл координат и файл топологии. Дан .gro-файл с 38 молекулами этана. Создадим индекс файл котором будет группа из одной молекулы этана:

make_ndx -f box_38.gro -o 1.ndx
r 1
q

Получили файл 1.ndx. Теперь создадим .gro-файл с одной молекулой, зададим ячейку и расположим молекулу в центре этой ячейки:

editconf -f box_38.gro -o et1.gro -n 1.ndx
3

editconf -f et1.gro -o et.gro -d 2 -c

Теперь построим файл топологии для этана, который выглядит примерно так: et_example.top. Но этот вариант топологии работать не будет, необходимо изменить типы атомов. Типы атомов находим в файле atomtypes.atp. Выбираем следующие типы:

opls_135   12.01100  ; alkane CH3 
opls_140    1.00800  ; alkane H.

Кроме того, в файле, данном в качестве примера, не хватает одной связи, необходимо ее добавить. Создаем файл et.top и проверяем, что он работает (предварительно скачав файл be.mdp):

grompp -f be.mdp -c et.gro -p et.top -o et_test.tpr

Параметры контроля температуры.

Даны 5 файлов с разными параметрами контроля температуры:

• be.mdp - метод Берендсена для контроля температуры;
• vr.mdp - метод "Velocity rescale" для контроля температуры;
• nh.mdp - метод Нуза-Хувера для контроля температуры;
• an.mdp - метод Андерсена для контроля температуры;
• sd.mdp - метод стохастической молекулярной динамики.

Сначала строим входные файлы для молекулярно-динамического движка mdrun с помощью grompp:

grompp -f ${i}.mdp -c et.gro -p et.top -o et_${i}.tpr
# где i: be,vr,nh,an,sd

В результате получилось 5 .tpr-файлов. Теперь для каждого из них запустим mdrun:

mdrun -deffnm et_${i} -v -nt 1

2. Анализ результатов.

Сначала проводим визуальный анализ. Для этого для каждой из 5 систем проводим конвертацию в pdb:

trjconv -f et_${i}.trr -s et_${i}.tpr -o et_${i}.pdb
2

Все молекулы в первом состоянии выглядят абсолютно одинаково и полностью накладываются друг на друга (рисунок 1). Молекулы этана находятся в заторможенной конформации.

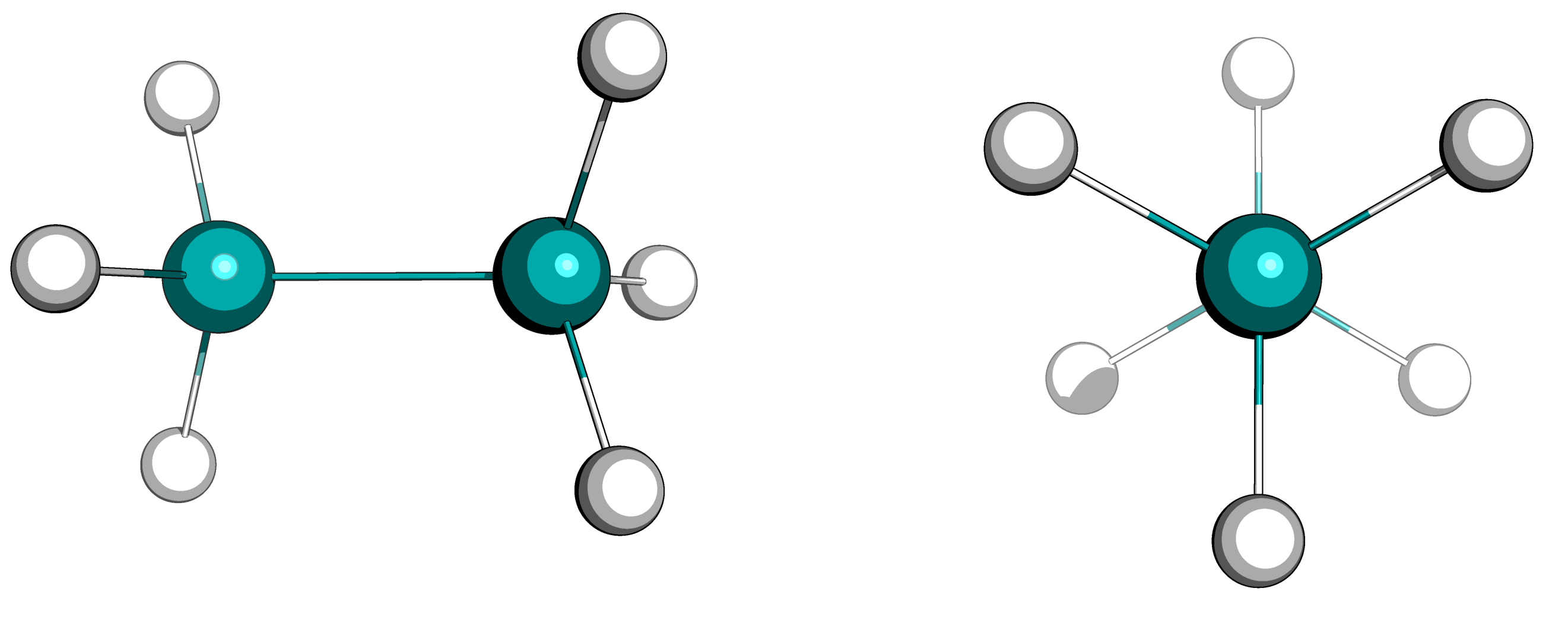
Рисунок 1. Молекула этана в двух проекциях. Для всех пяти файлов с параметрами контроля температуры молекулы получились абсолютно одинаковыми.

На видео 1-6 представлены колебания молекул этана в пяти рассматриваемых системах.

Видео 1. Движения молекулы этана, полученные методом Берендсена для контроля температуры. Если возникли проблемы с воспроизведением видео, его можно посмотреть на YouTube.	Видео 2. Движения молекулы этана, полученные методом "Velocity rescale" для контроля температуры. Если возникли проблемы с воспроизведением видео, его можно посмотреть на YouTube.
Видео 3. Движения молекулы этана, полученные методом Нуза-Хувера для контроля температуры. Если возникли проблемы с воспроизведением видео, его можно посмотреть на YouTube.	Видео 4. Движения молекулы этана, полученные методом Андерсена для контроля температуры. Если возникли проблемы с воспроизведением видео, его можно посмотреть на YouTube.
Видео 5. Движения молекулы этана, полученные методом стохастической молекулярной динамики для контроля температуры. Если возникли проблемы с воспроизведением видео, его можно посмотреть на YouTube.	Видео 6. Движения молекулы этана, полученные пятью различными методами для контроля температуры, рассмотренными ранее. Если возникли проблемы с воспроизведением видео, его можно посмотреть на YouTube.

Во всех системах наблюдается различное движение молекул этана. Во всех системах, кроме метода Нуза-Хувера, не происходит смены конформации. Во время движения, полученного методом Нуза-Хувера, молекула этана приходит в состояние заслоненной конформации (рисунок 2). В различных системах комбинируется колебательное движение (изменение длины связи) и вращательное движение вокруг различных осей.

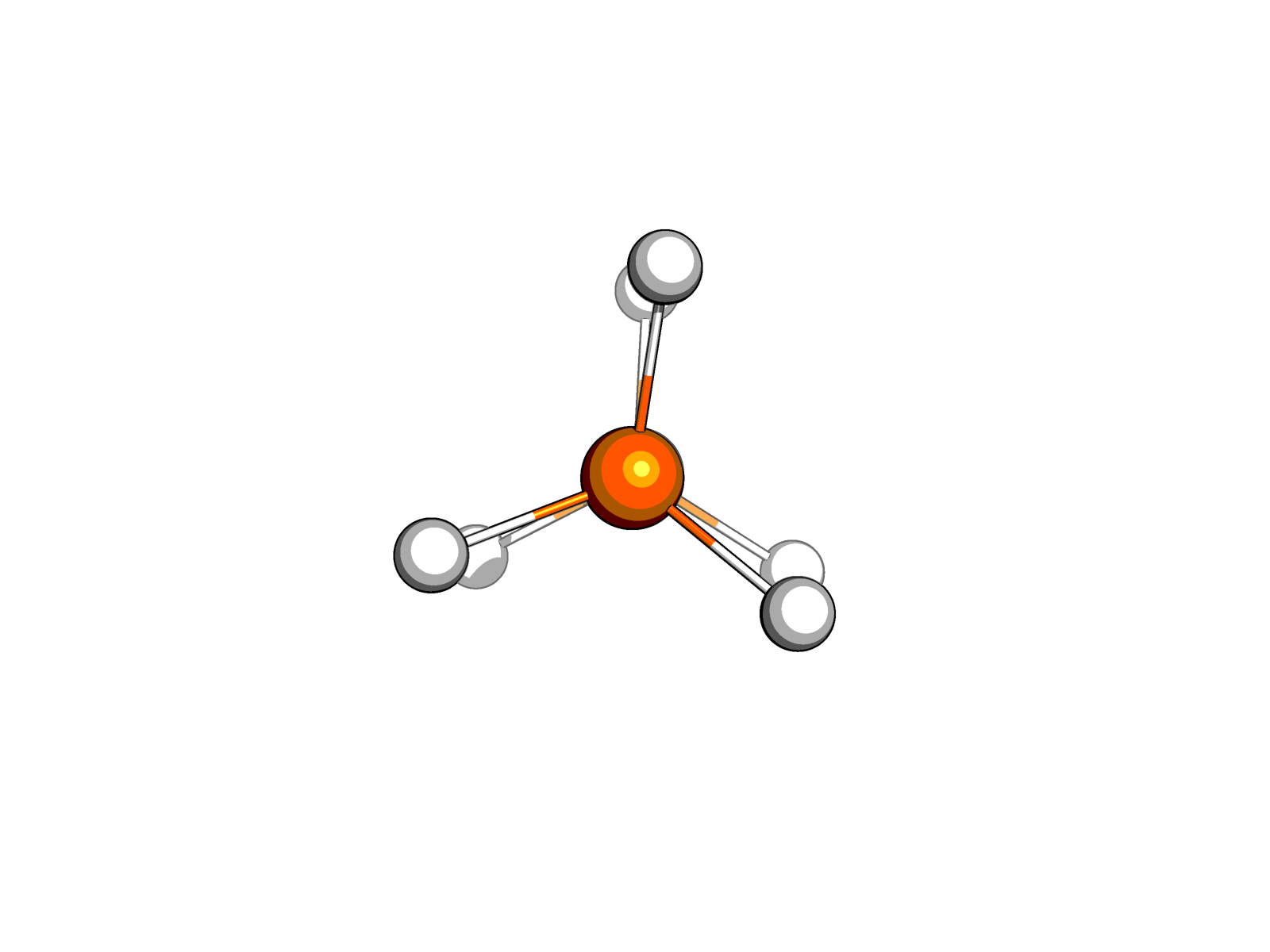
Рисунок 2. Молекула этана в заслоненной конформации.

Теперь сравним потенциальную энергию связи и кинетическую энергию для каждой из 5 систем:

g_energy -f et_${i}.edr -o et_${i}_en.xvg
10
11

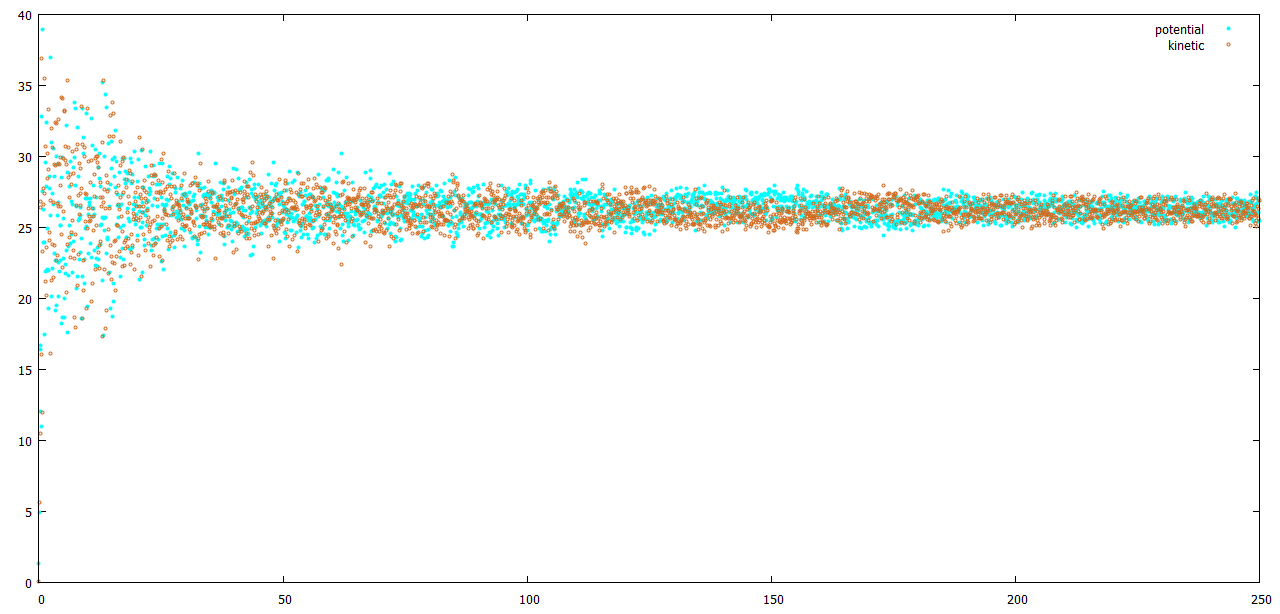
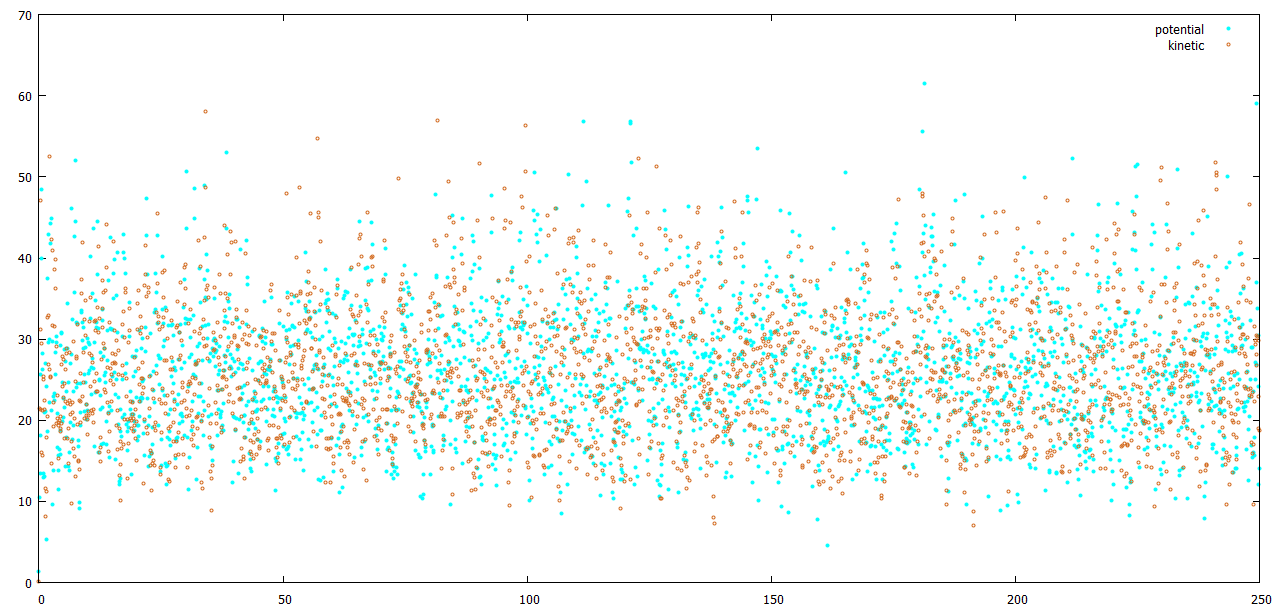
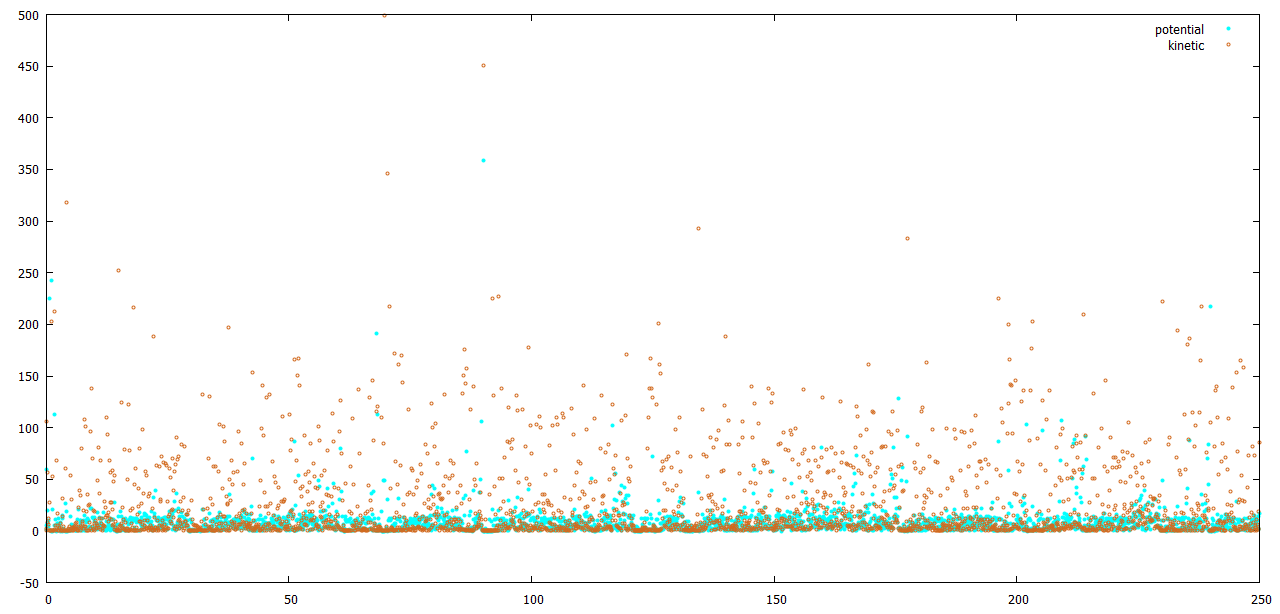
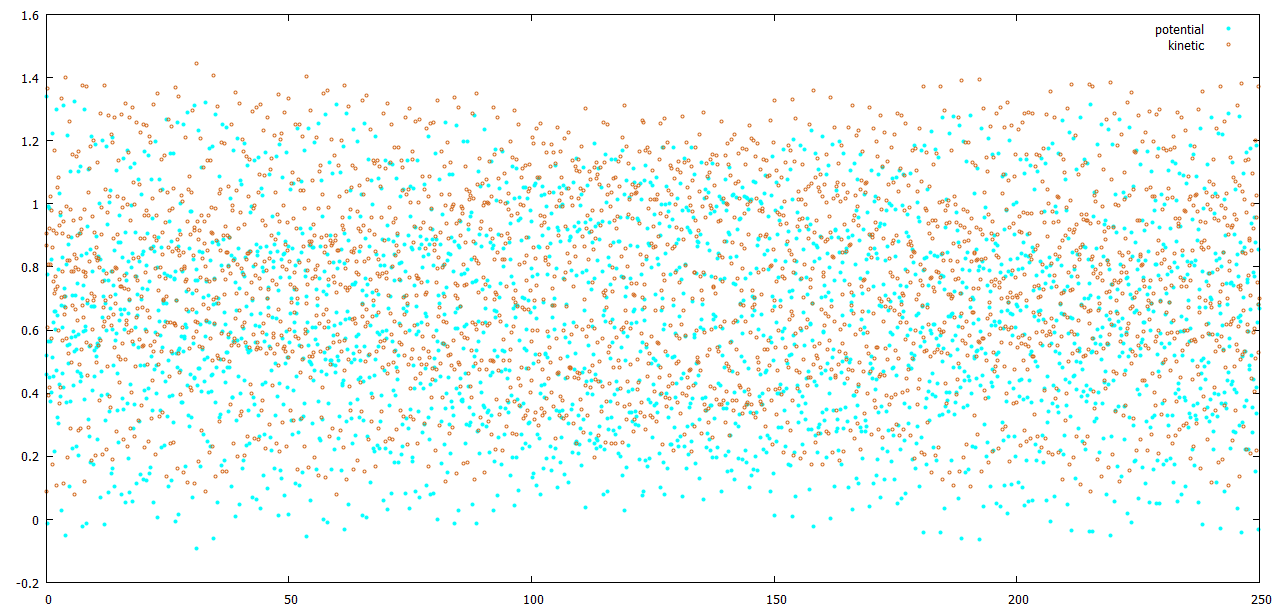
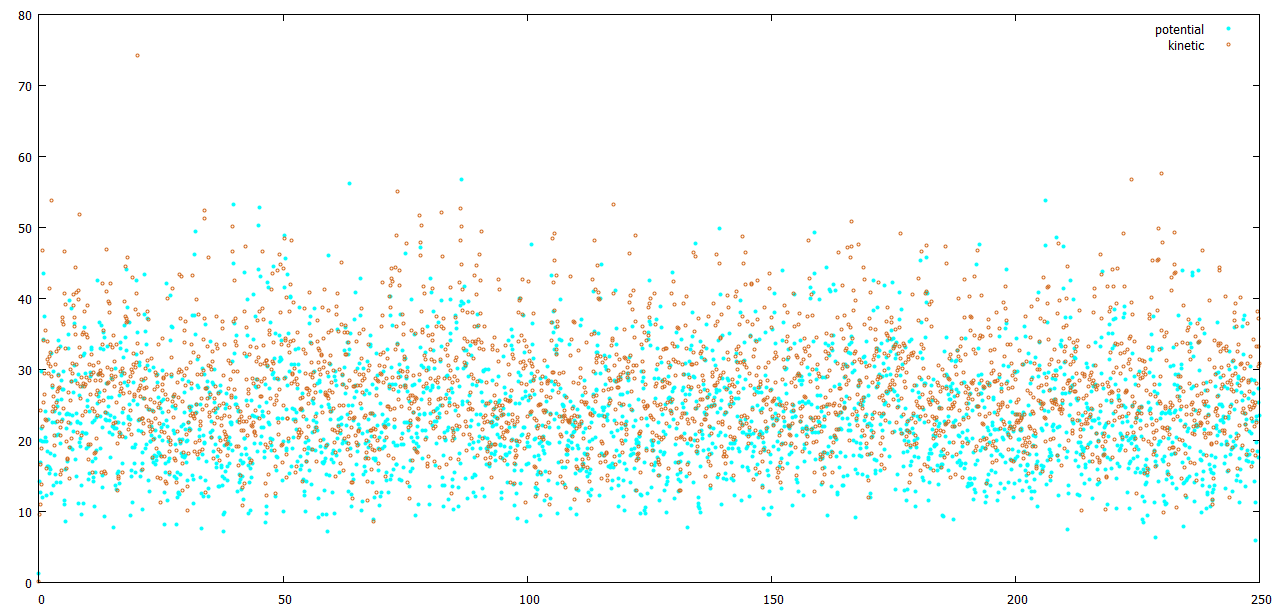
С помощью Gnuplot построим графики изменения энергий в виде dot-plot (рисунки 2-6):

plot "et_be_en.xvg" using 1:2 title "potential" \
	lt rgb "#00FFFF" pointtype 7 pointsize 0.5, \
	"et_be_en.xvg" using 1:3 title "kinetic" \
	lt rgb "#D2691E" pointtype 6 pointsize 0.5

Рисунок 3. График изменения энергий в системе с методом Берендсена для контроля температуры.	Рисунок 4. График изменения энергий в системе с методом "Velocity rescale" для контроля температуры.
Рисунок 5. График изменения энергий в системе с методом Нуза-Хувера для контроля температуры.	Рисунок 6. График изменения энергий в системе с методом Андерсена для контроля температуры.
Рисунок 7. График изменения энергий в системе с методом стохастической молекулярной динамики.

Из графиков видно, что значения кинетической и потенциальной энергий, а также их соотношение значительно отличаются для различных методов контроля температуры. Характер изменения энергий также различный для всех пяти систем.
Далее рассмотрим распределение длинны связи С-С за время моделирования. Сначала создадим индекс файл с одной связью b.ndx. Затем запустим утилиту по анализу связей g_bond:

g_bond -f et_${i}.trr -s et_${i}.tpr -o bond_${i}.xvg -n b.ndx

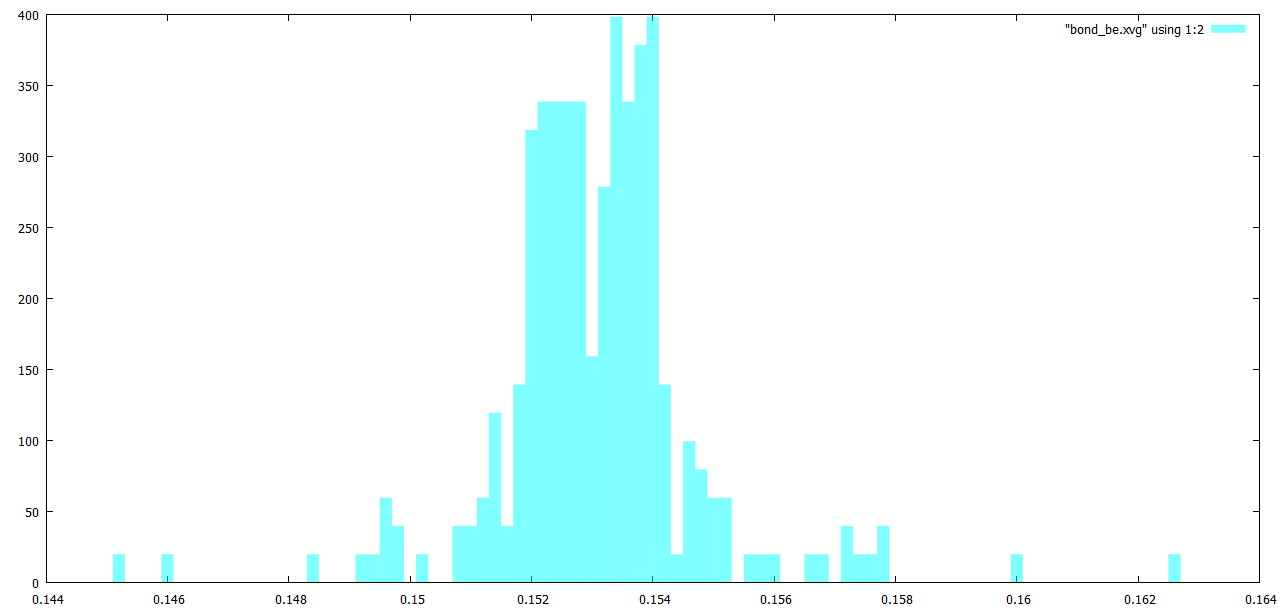
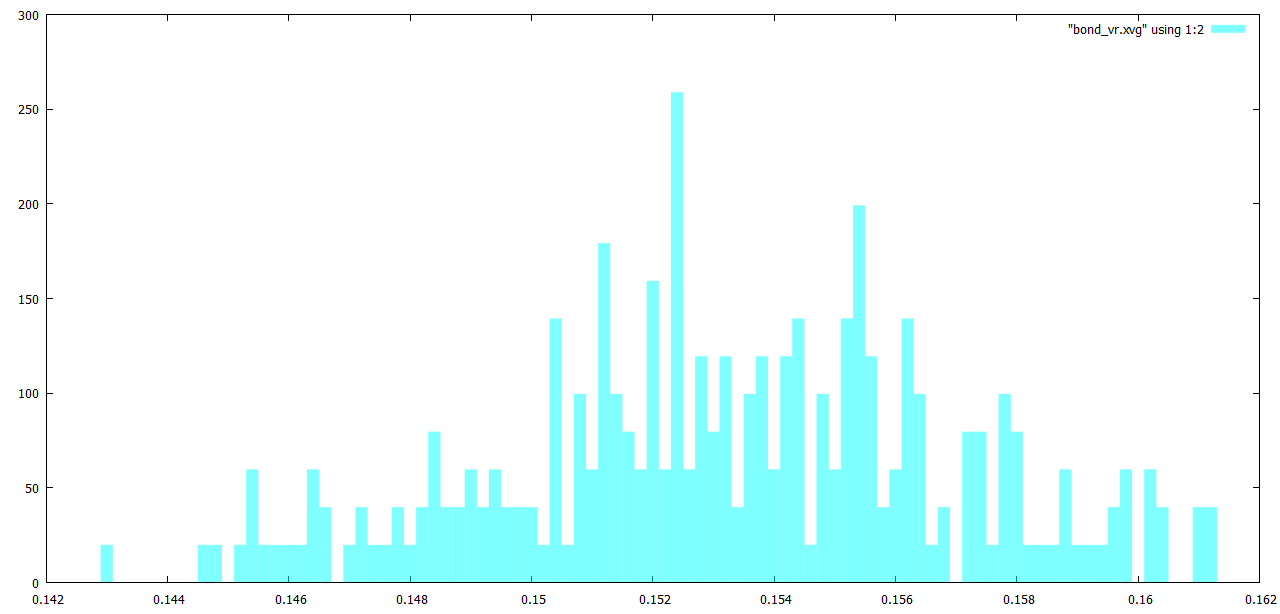
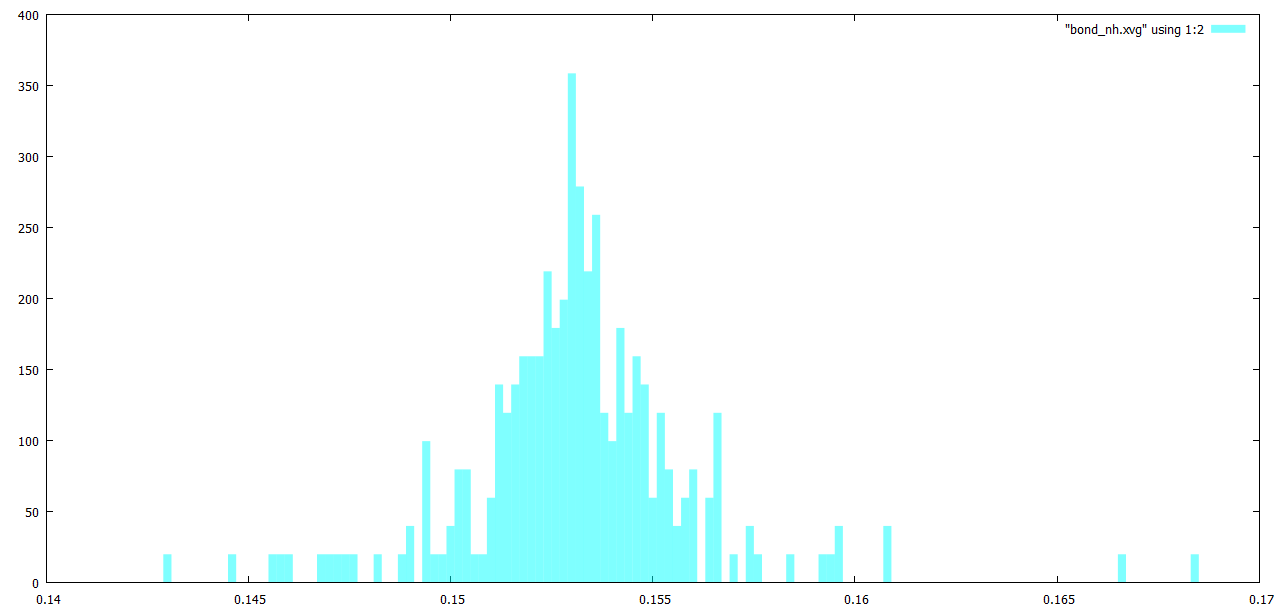
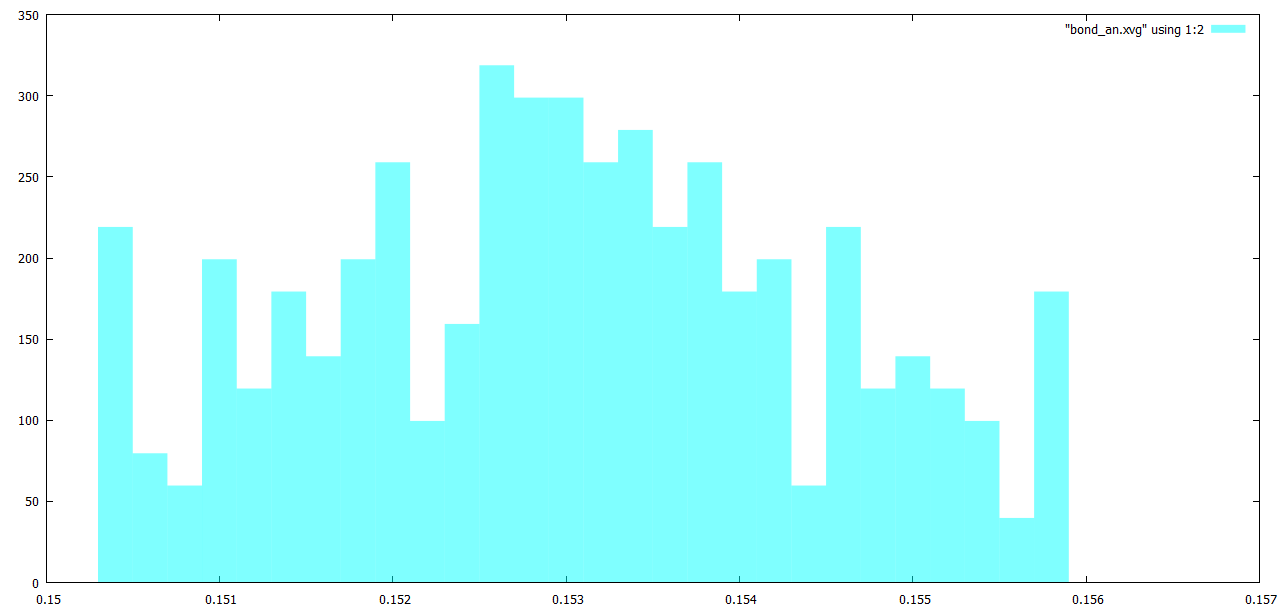
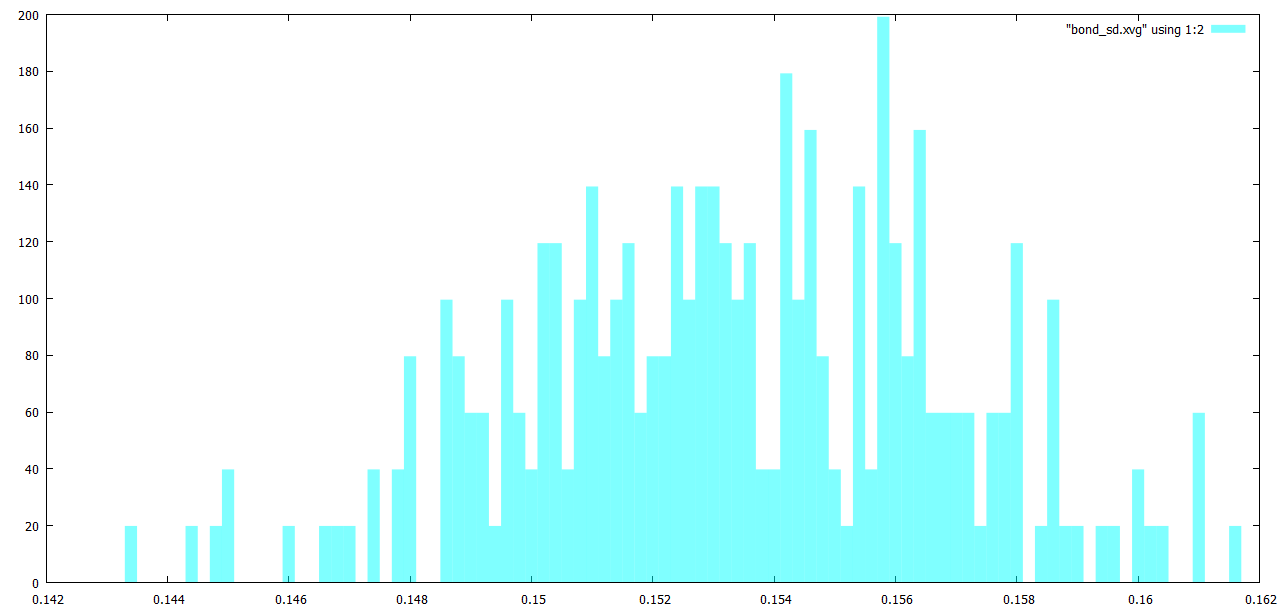
Наконец в Gnuplot построим гистограммы распределения длинн связей (рисунки 8-12):

plot "bond_be.xvg" using 1:2 w boxes lc rgb "#00FFFF"

Рисунок 8. Распределение длинн связей в системе с методом Берендсена для контроля температуры.	Рисунок 9. Распределение длинн связей в системе с методом "Velocity rescale" для контроля температуры.
Рисунок 10. Распределение длинн связей в системе с методом Нуза-Хувера для контроля температуры.	Рисунок 11. Распределение длинн связей в системе с методом Андерсена для контроля температуры.
Рисунок 12. Распределение длинн связей в системе с методом стохастической молекулярной динамики.

На распределение Больцмана больше всего похожи графики для методов стохастической молекулярной динамики и "Velocity rescale". Графики для методов Берендсена и Нуза-Хувера больше похожи на нормальное распределение. График для метода Андерсена вообще ни на что не похож.
Все файлы, использованные и полученные во время выполнения задания, доступны в папке.

Бонус:

(смотреть со звуком)

Если возникли проблемы с воспроизведением видео, его можно посмотреть на YouTube.