Восстановление ЭП

Скачали и установили библиотеки numpy и matplotlib, скопировали модуль fourier.py.

Создание модельной функции ЭП в одномерной элементарной ячейке

На отрезке [0,30] (ангстремы) расположены две молекулы: H-O-H---H-N-C-.

Эта модель из двух молекул (3+3), реализуем проекцию.

Электронные плотности (ЭП) атомов описываются гауссовой кривой, зададим функцию командой:

python compile-func.py -g 2,3.5,3+40,3,4.3+2,3.5,5.6+2,3.5,9.1+29,3,10.4+28,3,11.7

Это сумма гауссовых функций, где 1.3 - расстояние между атомами, а 3.5 - водородная связь между молекулами, для водорода ширину "колокола" берем чуть больше - 3.5, а не 3, 2, 40, 29, 28 - высоты "колоколов", разные для разных атомов. Получили 1D модель электронной плотности молекул. Функция задается в виде суммы гармоник.

Расчет параметров сигнала, моделирующих экспериментальные данные: амплитуды и фазы

Амплитуды и фазы рассчитываются по входной функции ЭП.

Разложили функцию на гармоники, используя ее описание, командой:

python func2fourier.py -i func.txt -o harmon.txt

Выходной файл имеет формат: <номер гармоники> <амплитуда> <фаза>.

Ссылка на полученный файл

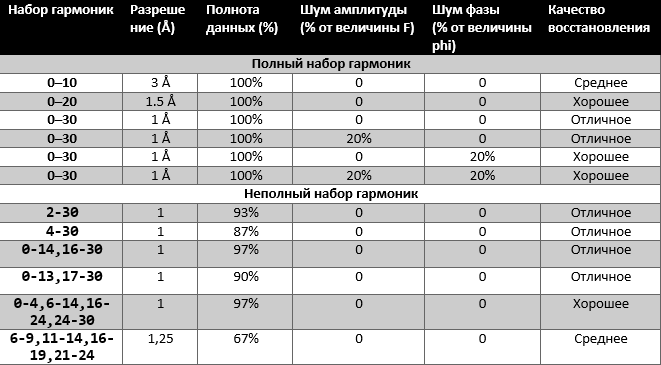
Восстановили исходную функцию по полному набору гармоник (рис. 1).

python fourier2func.py -i harmon.txt -o func_all.txt -s

-s отключает исходную функцию.

Рис. 1. График восстановленной функции, совпал с исходным.

Восстановление функции ЭП с разным размрешением

Номера гармоник: 0 – гармоника - константа, длины волны нет, 1 – длина волны равна длине отрезка T/1 (T=30 Å). Если брать набор из 10 гармоник, получим разрешение ~ 3 Å, из 20 - 1,5 Å, из 30 - 1 Å, очень близко к радиусу водорода. Для этих неполных наборов гармоник построили графики и посмотрели, как будет изменяться точность в таких случаях.

python fourier-filter.py -i harmon.txt -o  four_х.txt -r 0-х
python fourier2func.py -i four_х.txt -o func_х.txt

х=10,20 или 30.

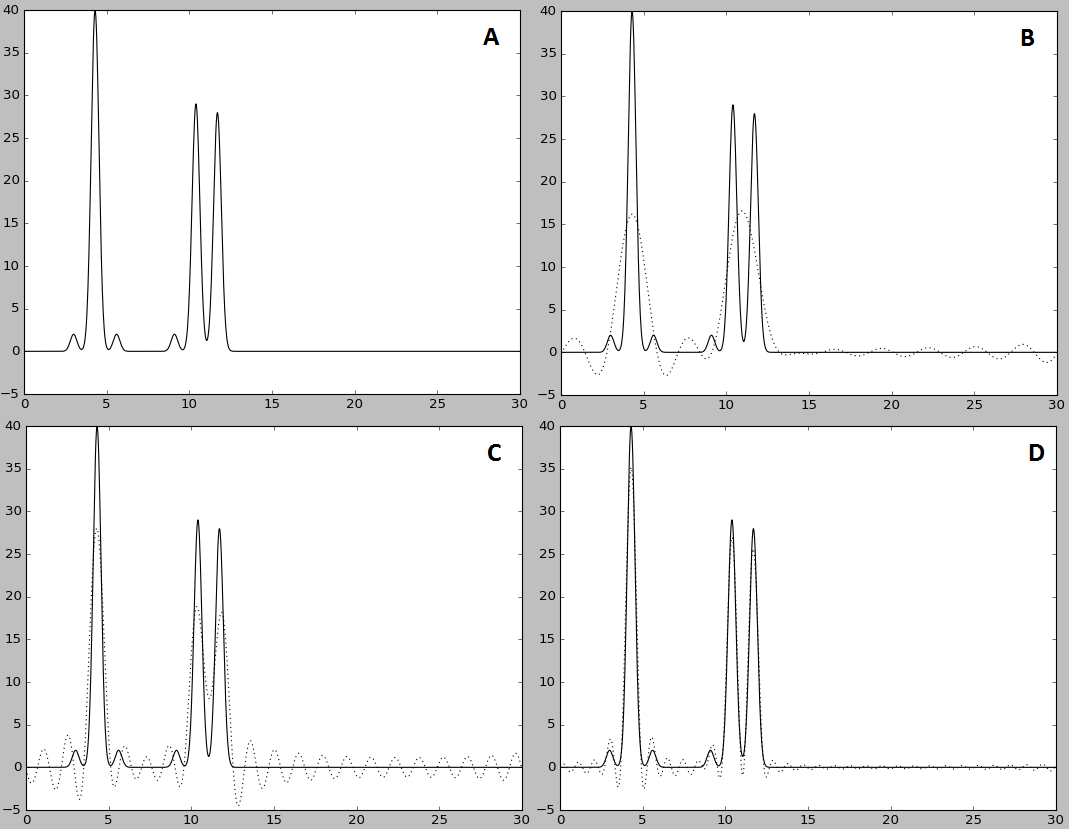
Рис. 2. A - восстановление по всем гармоникам; B - по 0-10, наблюдали сильное искажение; C - по 0-20, пики водородов сложно отличить от шума; D - по 0-30, отличное восстановление (по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")).

Затем был определён минимальный порог числа гармоник, при котором функция хорошо восстанавливается. Было проведено восстановление функции электронной плотности по 10 (разрешение 3?), 15(2?), 20 (1,5?), 25 (1,2?) и 30 (0,94?) гармоникам

При моделировании экспериментальных данных нужно учитывать, что в эксперименте, во-первых, определяются амплитуды не для всех сигналов; во-вторых, интенсивности сигналов (следовательно, и амплитуды) определяются с ошибкой; в-третьих, фазы определятся для всех измененных сигналов, но тоже с ошибкой.

Восстановление функции ЭП по неполному набору гармоник

Посмотрели, как восстановление по неполному набору гармоник будет влиять на качество восстановления. Пример команды:

python fourier-filter.py -i harmon.txt -o  four_ohne51525.txt -r 0-4,6-14,16-24,24-30
python fourier2func.py -i four_ohne51525.txt -o func_ohne51525.txt

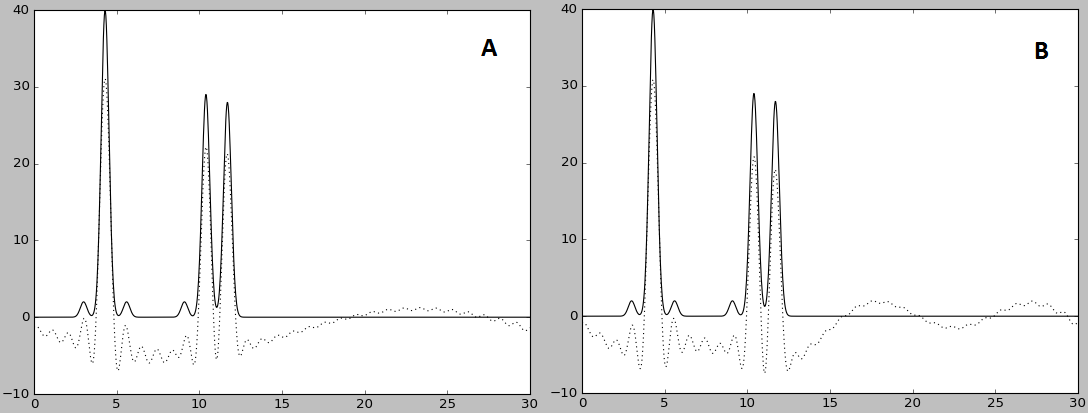
Рис. 3. A - восстановление без первой (-r 2-30); B - без первых трех (-r 4-30), происходит смещение, но пики соответствуют действительности и читаемы.

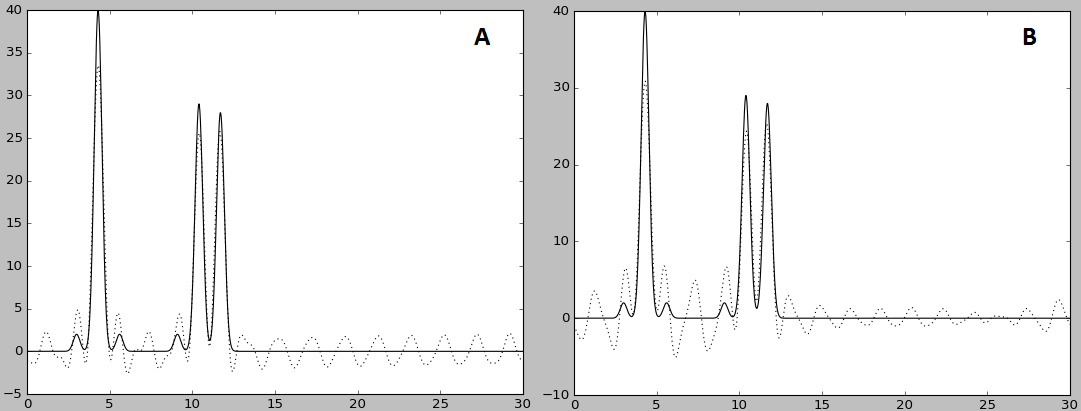
Рис. 4. A - восстановление без пятнадцатой (-r 0-14,16-30); B - без четырнадцатой-шестнадцатой - в середине (-r 0-13,17-30).

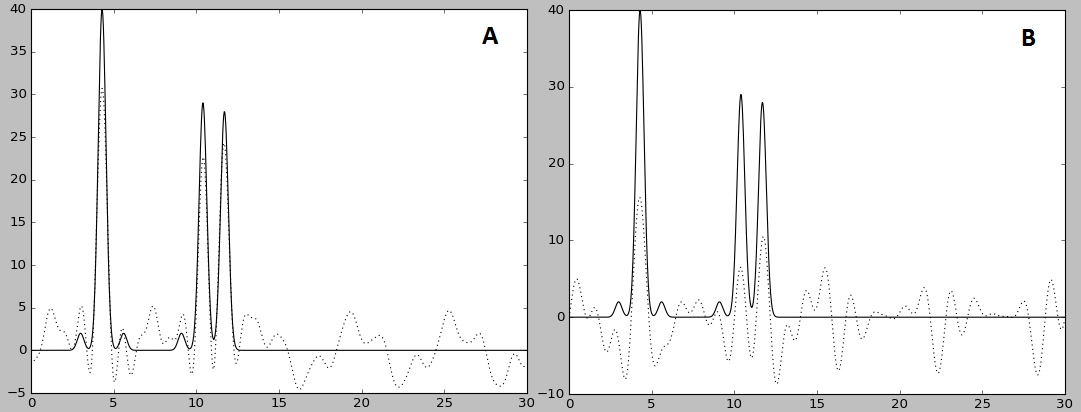
Рис. 5. A - восстановление без трех: 5, 15, 25 (-r 0-4,6-14,16-24,24-30), искажение сильнее, чем при удалении первых; B - захотелось получить сильнее искажение, пришлось много удалить (-r 6-9,11-14,16-19,21-24).

Восстановление функции ЭП с шумом

Добавление гауссового шума к амплитудам и фазам искажает все вычисленные амплитуды и фазы (подставим в команду: параметр -F <число> для внесения ошибок в вычисление амплитуд по структурным факторам и -P <число> для фазовых ошибок. Пример команды (нужно было изменить файл, оставив 30 гармоник):

python func2fourier.py -i func.txt -o harmon_both20.txt -F 20 -P 20
python fourier2func.py -i harmon_both20.txt -o func_new_both20.txt

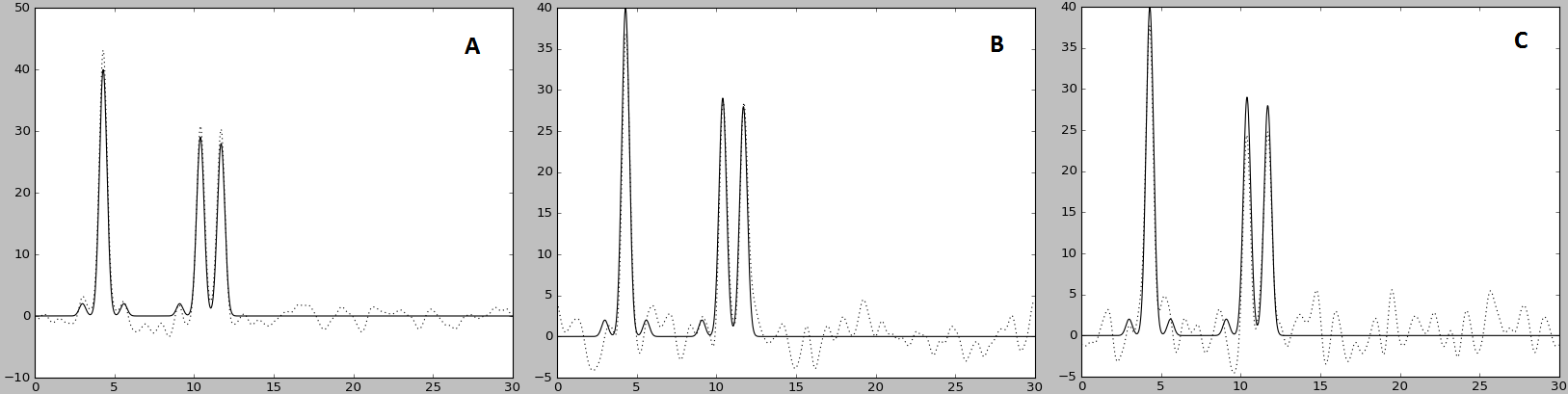
Рис. 6. A - восстановление с искажением амплитуд (-F 20 -P 0); B - искажение фаз (-F 0 -P 20); C - искажение по обоим параметрам (-F 20 -P 20).

Искажение фаз имеет большее влияние на результаты, чем искажение амплитуд при тех же параметрах, в настоящих экспериментах это представляет неудобства в связи с фазовой проблемой и особенностями рентгено-структурного анализа.

Оценка качества восстановления функции ЭП