Восстановление функции электронной плотности
Цель и задачи
Цель данной работы заключается в исследовании качества восстановления функции ЭП от одной переменной в зависимости от того, какие и сколько гармоник ряда Фурье используются для ее восстановления.
Задание включает следующие этапы:
- Создание модельной функции ЭП в одномерной элементарной ячейке
- Расчет параметров сигнала, моделирующих экспериментальные данные: амплитуды и фазы
- Восстановление функции ЭП по модельным ("экспериментальным") данным
- Оценка качества восстановления функции ЭП
Создание модельной функции ЭП в одномерной элементарной ячейке
Была создана линейная атомная модель для компьютерного эксперимента: 2 линейных молекулы O-C-O и Cl-Hg-Cl. Для этой модели была смоделирована функция, описывающая одномерную электронную плотность (ЭП) с помощью скрипта compile-func.py:
ЭП атомов описываются гауссовской кривой, максимум в центре атома приблизительно пропорционален числу электронов в атоме. Функция задается на интервале [0Å, 30Å]. Гауссова функция определяется числами lambda, beta, gamma по формуле:
lambda - высота гауссовской кривой, соответствующая максимуму электронной плотности в центре атома. Пропорционально числу электронов в атоме:
- O - 32
- C - 12
- Hg - 201
- Cl - 71
beta - ширина колокола, которая примерно соответствует диаметру атома:
- O - 1.46
- C - 1.82
- Hg - 2.98
- Cl - 2.04
gamma - координата максимума гауссовой кривой. Расстояние между молекулами - 5.5 Å, длина всех связей - 1.5 Å. График электронной плотности модели атомов представлен на рисунке 1. Поточенчные координаты приведены в файле func.txt.
По оси абсцисс отложены кординаты атомов в Å, а по оси ординат отложена амплитуда ЭП в условных единицах.
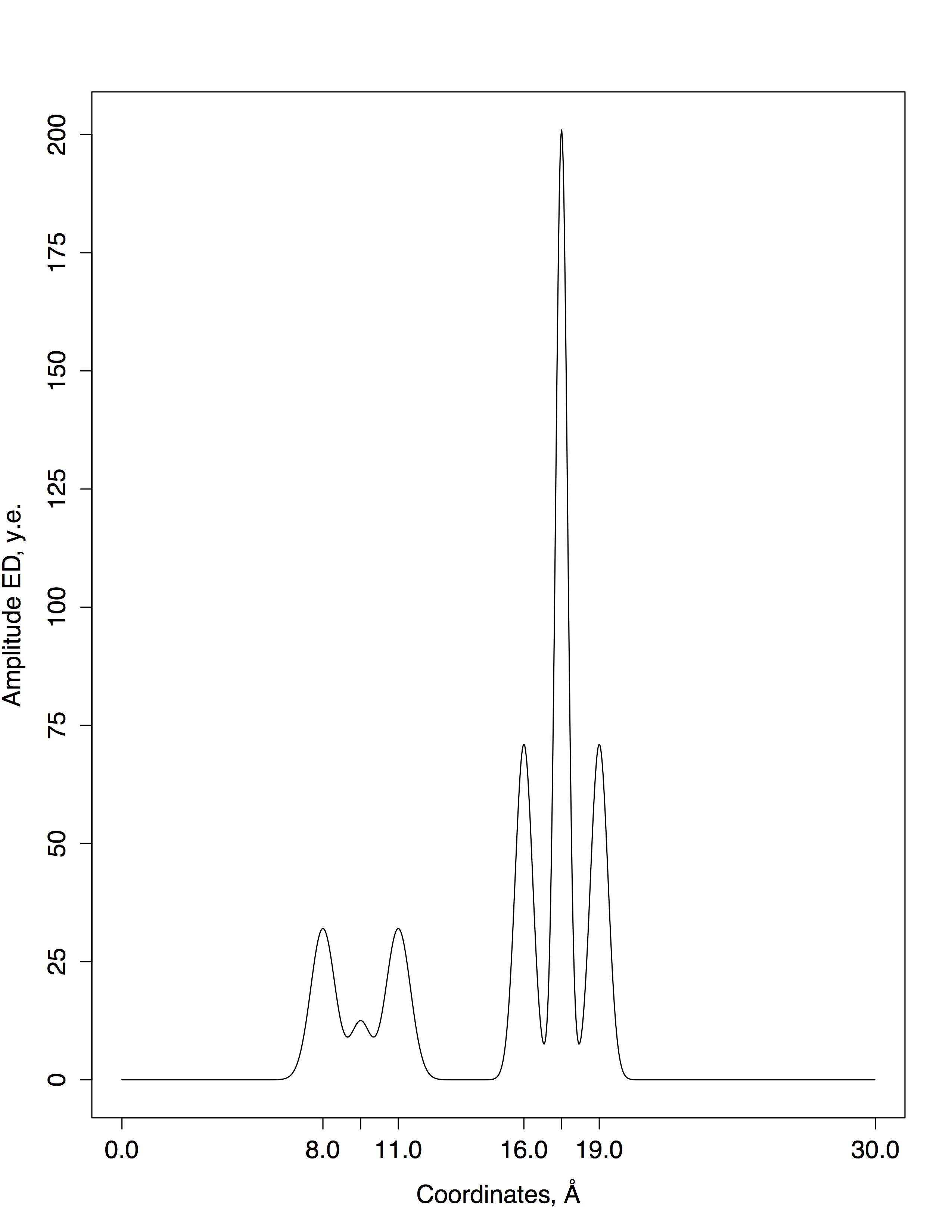
Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные
Рассчет коэффициентов Фурье
Амплитуды и фазы рассчитываются по входной функции ЭП. При моделировании экспериментальных данных учитывается, что в эксперименте, во-первых, определяются амплитуды не для всех сигналов; во-вторых, интенсивности сигналов (следовательно, и амплитуды) определяются с ошибкой; в-третьих, фазы определятся для всех измененных сигналов, но тоже с ошибкой.
Коэффициенты Фурье рассчитываются с помощью скрипта func2fourier.py следующей командой:
Скрипт по ранее полученному файлу func.txt выдает 499 гармоник на отрезке [0 Å, 30 Å]. Выходной файл скрипта – файл func_ft.txt. Выходной файл имеет формат: <номер гармоники> <амплитуда> <фаза>.
Отбор гармоник
Набор гармоник ряда Фурье называется полным, если известны все гармоники с номерами 0, 1, 2, ..., n. Разрешением полного набора гармоник называется период гармоники с номером n, то есть с наибольшим номером. Период гармоники равен расстоянию между соседними максимумами синусоиды. Его также называют длиной волны этой гармоники. Зависимость длины волны гармоники от номера:
- 0 – гармоника есть константа, длины волны нет
- 1 – длина волны равна длине отрезка T (в нашем случае T = 30 Å)
- 2 – — " — T/2
- ...............
- n – — " — T/n
Отбор гармоник для получения неполного набора можно сделать одним из способов:
- Скопировать файл с коэффициентами Фурье и убрать лишние строки.
- Пометить лишние строки знаком "#" в первой позиции строки (такие строки при чтении игнорируются).
- Запустить скрипт fourier-filter.py, который отфильтрует нужные строки.
Мы будем пользоваться последним способом.
Восстановление функции ЭП по амплитудам и фазам части сигналов
Полные наборы гармоник
По полному набору гармоник был построен график восстановленной функции электронной плотности модели с помощью скрипта fourier2func.py командой:
Сравнение графика восстановленной функции и графика первоначальной функции можно увидеть на рис.2. Очевидно, что при количестве гармоник, равном 499, получается отличное восстановление, т.е. по графику восстановленной функции можно определить положение максимумов всех гауссовых слагаемых. При таком количестве гармоник разрешение составляет ... Å (разрешением полного набора гармоник называется период гармоники с номером n, тo есть с наибольшим номером. Период гармоники равен расстоянию между соседними максимумами синусоиды). Это довольно высокое значение.
По оси абсцисс отложены кординаты атомов в Å, а по оси ординат отложена амплитуда ЭП в условных единицах.
| A. График первоначальной функции | B. График восстановленной функции |
 |
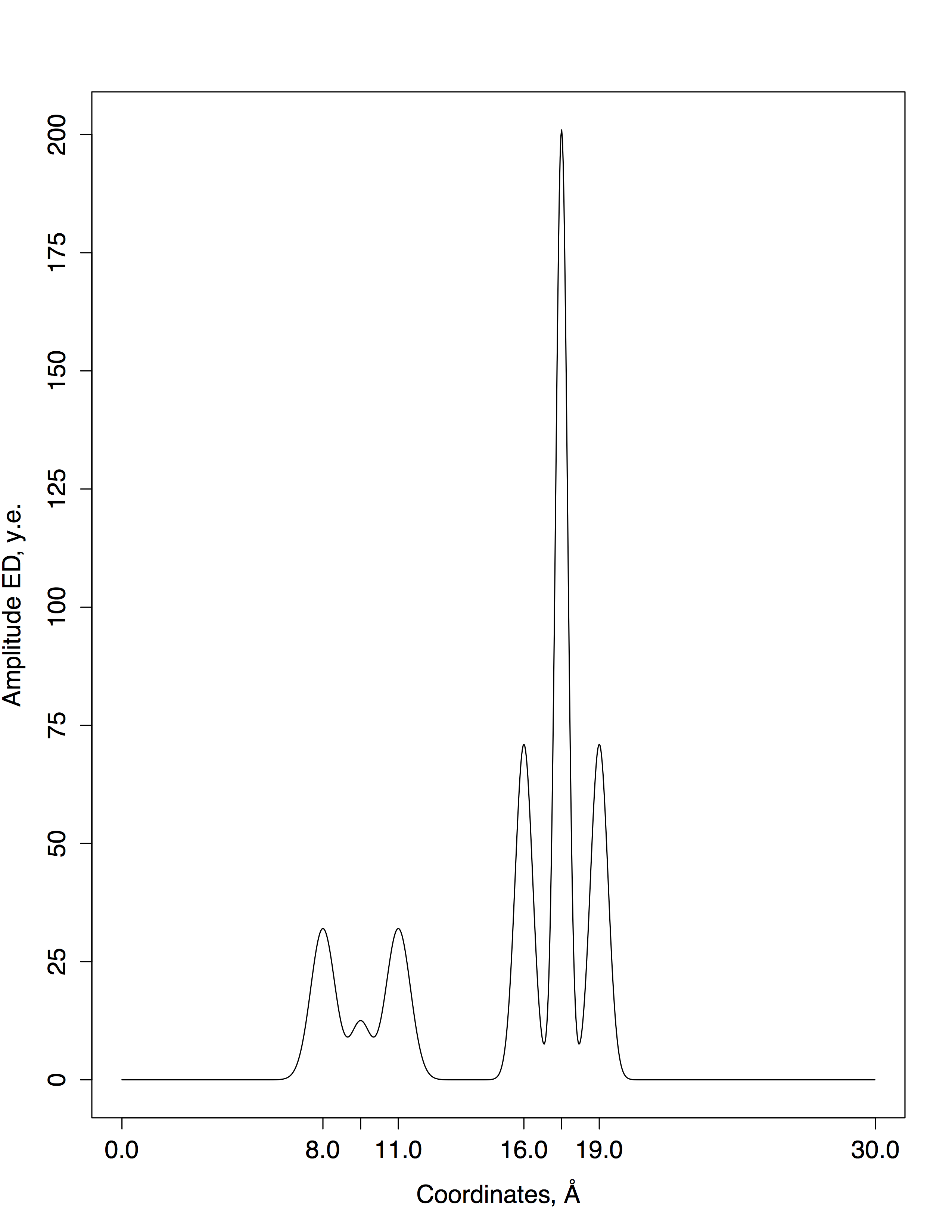 |
Найдем минимальное число гармоник, при котором восстановление функции сохранится отличным. Для этого рассмотри n-первых гармоник, где n = 2, 21, 26, 31, 41.
python fourier2func.py -f func.txt -i ffr_1.txt -o ffc_1.txt
python fourier-filter.py -r 0-5 -i func_ft.txt -o ffr_5.txt
python fourier2func.py -f func.txt -i ffr_5.txt -o ffc_5.txt
python fourier-filter.py -r 0-10 -i func_ft.txt -o ffr_10.txt
python fourier2func.py -f func.txt -i ffr_10.txt -o ffc_10.txt
python fourier-filter.py -r 0-15 -i func_ft.txt -o ffr_15.txt
python fourier2func.py -f func.txt -i ffr_15.txt -o ffc_15.txt
python fourier-filter.py -r 0-20 -i func_ft.txt -o ffr_20.txt
python fourier2func.py -f func.txt -i ffr_20.txt -o ffc_20.txt
python fourier-filter.py -r 0-30 -i func_ft.txt -o ffr_30.txt
python fourier2func.py -f func.txt -i ffr_30.txt -o ffc_30.txt
Как сравнить восстановленную функцию с исходной?
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов");
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума;
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно;
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".
Графики восстановленных функций, представленны красной линией, для A. - 0-1; Б. - 0-5; В. - 0-10; Г. - 0-25; Д. - 0-20 и Е. - 0-30 наборов гармоник. Исходная функция – представлена в виде сплошной линии.
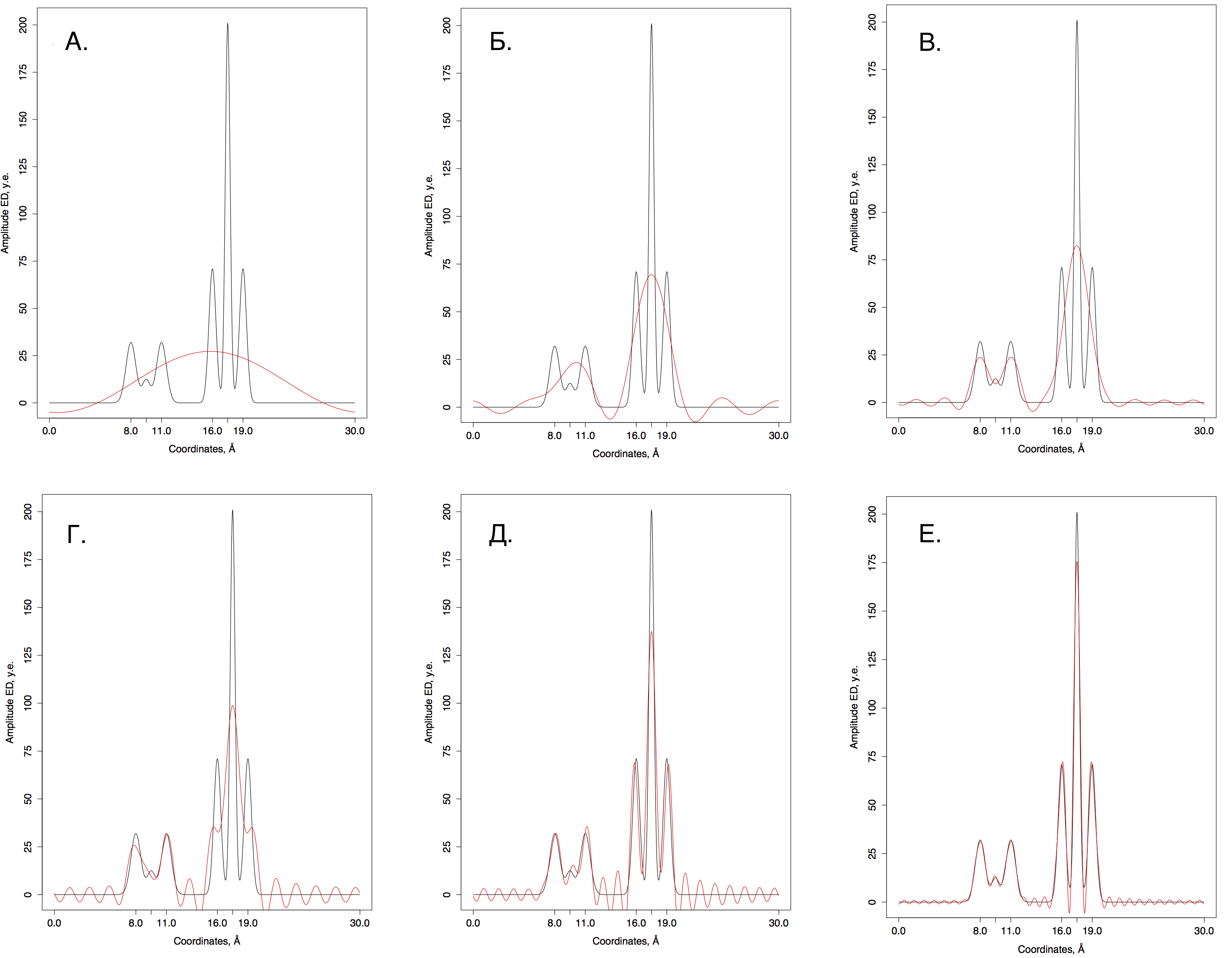
Исходя из графиков на рис.2, видно, что 31 - это минимальное число гармоник (n0), при котором функция сохраняет отличное восстановление.
Добавим шум к амплитудам и фазам при восстановлении по полному набору гармоник. Добавление гауссового шума к амплитудам (параметр -F <число>) и фазам (-P <число>) искажает все вычисленные амплитуды и фазы. Пример: -F 20 (шум 20%) приводит к тому, что к каждой амплитуде прибавляется случайное число, распределенное нормально с параметрами: среднее=0, среднее квадратичное отклонение σ=0.2*F. Аналогично действует параметр -P <число>. Добавим 10% шума только к амплитудам, только к фазам, по 5 % к амлитудам и фазам:
python func2fourier.py -F 10 -i func.txt -o noise_f10.txt
python fourier-filter.py -r 0-30 -i noise_f10.txt -o noise_f10_30.txt
python fourier2func.py -i noise_f10_30.txt -o func_noise_f10_30.txt
Добавление шума только к фазе
python func2fourier.py -P 10 -i func.txt -o noise_p10.txt
python fourier-filter.py -r 0-30 -i noise_p10.txt -o noise_p10_30.txt
python fourier2func.py -i noise_p10_30.txt -o func_noise_p10_30.txt
Добавление шума к амплитуде и к фазе
python func2fourier.py -F 5 -P 5 -i func.txt -o noise_f5p5.txt
python fourier-filter.py -r 0-30 -i noise_f5p5.txt -o noise_f5p5_30.txt
python fourier2func.py -i noise_f5p5_30.txt -o func_noise_f5p5_30.txt
Графики изначальной функции электронной плотности (черная линия) и восстановленной (красная линия) для 31 гармоник A. - с шумом 10% к амплитуде; Б. - 10% к фазе; В - по 5% к амплитуде и фазе.
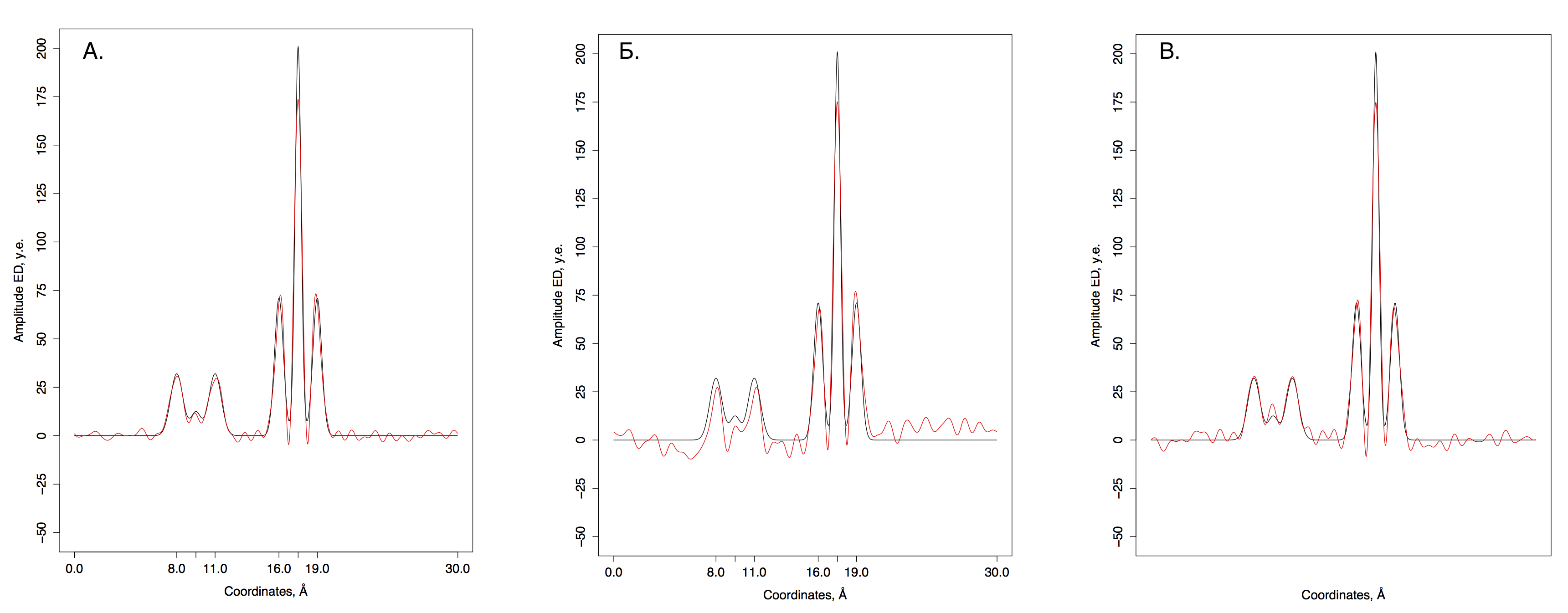
Неполные наборы гармоник
Сделаем неполные наборы гармоник для набора n0: удалим несколько первых гармоник, удалим серединные гармоники, добавим гармонику с номером n0+10.
-
Удаление первой гармоники
- python fourier-filter.py -r 1-30 -i func_ft.txt -o ft_begin.txt
python fourier2func.py -i ft_begin.txt -o begin_1.txt
Удаление первых трех гармоник
- python fourier-filter.py -r 3-30 -i func_ft.txt -o ft_begin.txt
python fourier2func.py -i ft_begin.txt -o begin_3.txt
python fourier-filter.py -r 0-15,19-30 -i func_ft.txt -o ft_mid.txt
python fourier2func.py -i ft_mid.txt -o func_mid.txt
Добавление гармоники с номером n0+10
python fourier-filter.py -r 0-30,40 -i func_ft.txt -o ft_append.txt
python fourier2func.py -i ft_append.txt -o func_append.txt
При удалении нулевой гармоники функция заметно смещается вниз по оси ординат. Это можно объяснить тем, что эта гармоника есть константа, длины волны у нее нет. Если же удалить первые три, то вычитается синусоида с периодом T/3. Видно, что в этом случае мы наблюдаем "провал" амплитуды для средних значений координат.
Графики восстановленных функций, представленны красной линией, для A. - Удаление первой гармоники; Б. - Удаление первых трех гармоник; В. - Удаление 5-10% гармоник из середины набора; Г. - Добавление гармоники с номером n0+10. Исходная функция – представлена в черной линией.
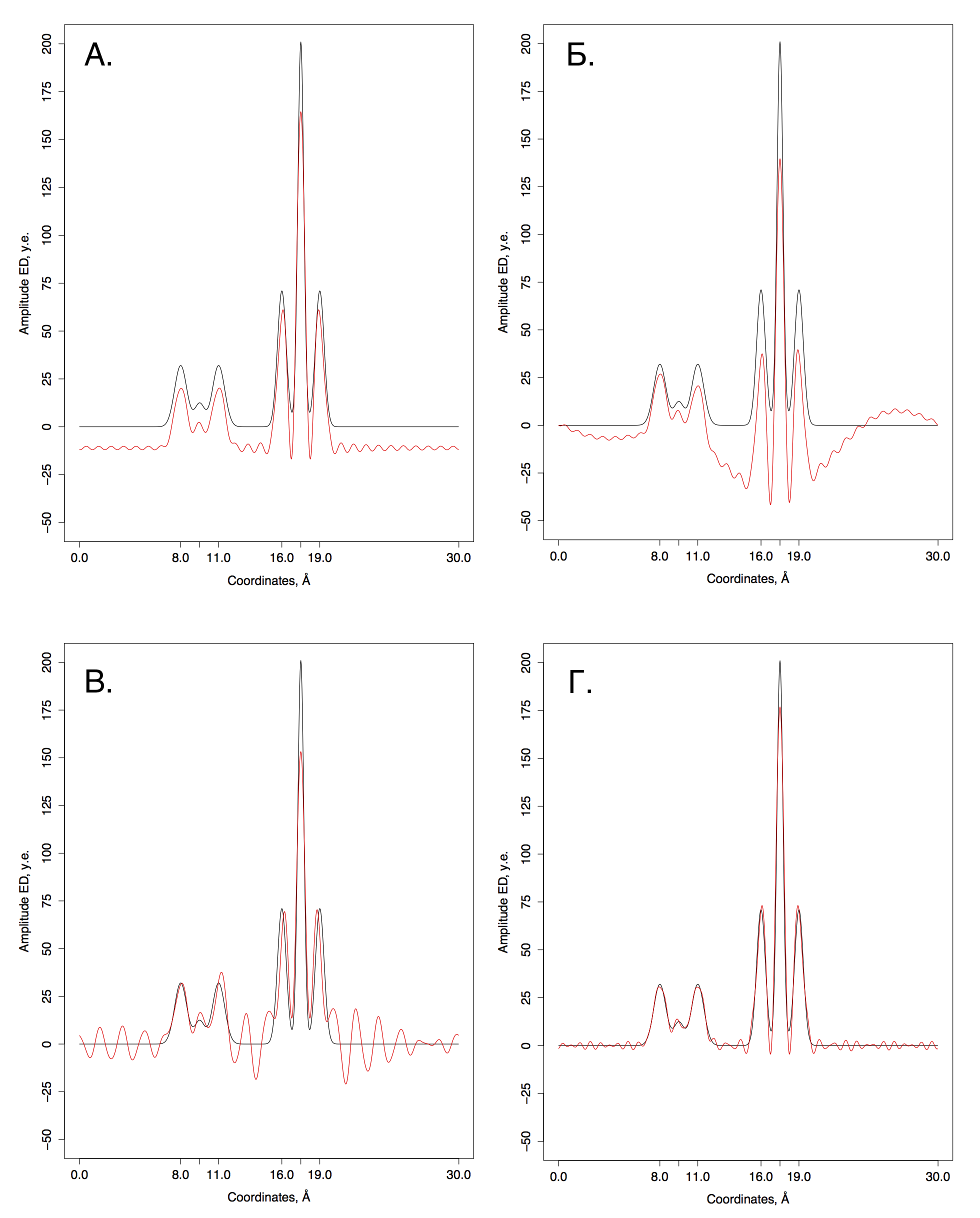
Вследствие удаления 10% гармоник в середине набора качество восстановления сильно ухудшилось, максимумы от атомов стали почти не отличимы от шума. Добавление гармоники с номером 40 к набору гармоник n0 немного "дестабилизировали" шум, по сравнению с просто набором гармоник n0. То есть шум стал как бы неравномерным, а где-то меньше, где-то больше. Из всего выше сказанно можно сделать вывод, что чем больше номер гармоники, тем меньший вклад она вносит в общий вид восстановленной функции ЭП. Это логично, так как с увеличением номерам период гармоники уменьшается.
Cравнение восстановленной функцию с исходной
Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо сообщить полноту данных — процент гармоник с длиной волны большей d от максимально возможного, присутствующих в наборе. Для полного набора данных (разрешение d=T/n) полнота равна 100%. Рассмотрим алгоритм поиска разрешения для неполного набора гармоник (0-30, 40). Если применить разрешение для полного набора, то получится, что разрешение = 0.75, а полнота данных всего 80% (=32/40). Поэтому разумнее ввести порог на полноту данных 90% и пересчитать наше разрешение.
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум амплитуды (% от F) | Шум фазы (% от phi) | Качество восстановления |
| Полный набор гармоник | |||||
| 0-498 | 0.06 | 100 | 0 | 0 | отличное |
| 0-1 | 30 | 100 | 0 | 0 | плохое |
| 0-5 | 6 | 100 | 0 | 0 | плохое |
| 0-10 | 3 | 100 | 0 | 0 | среднее |
| 0-15 | 2 | 100 | 0 | 0 | среднее |
| 0-20 | 1.5 | 100 | 0 | 0 | хорошее |
| 0-30 | 1 | 100 | 0 | 0 | отличное |
| 0-30 | 1 | 100 | 10 | 0 | отличное |
| 0-30 | 1 | 100 | 0 | 10 | среднее |
| 0-30 | 1 | 100 | 5 | 5 | хорошее |
| Неполный набор гармоник | |||||
| 1-30 | 1 | 96.7 | 0 | 0 | отличное |
| 3-30 | 1 | 0.9 | 0 | 0 | хорошее |
| 0-15, 19-30 | 1 | 93.3 | 0 | 0 | среднее |
| 0-30, 40 | 1 | 100 | 0 | 0 | отличное |
