Ряд Фурье
Полный набор гармоник
Моделирование функции распределения электронной плотности
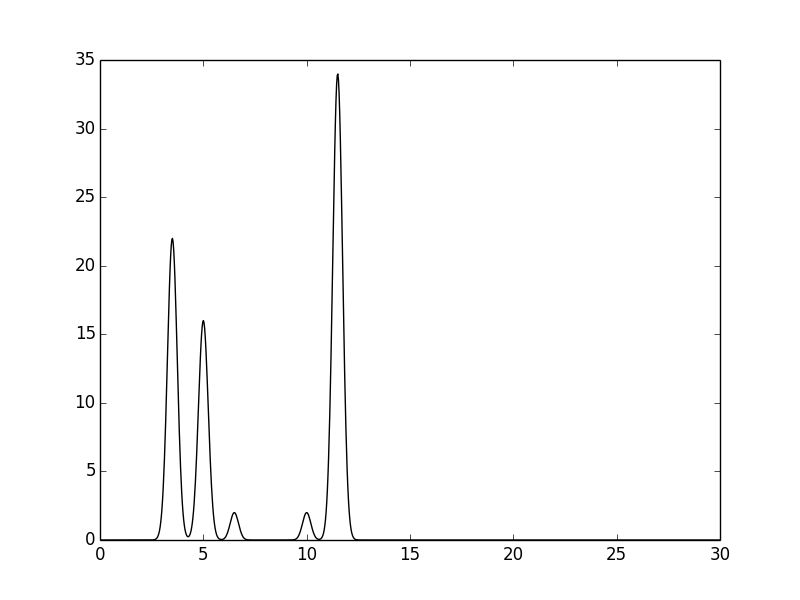
Была построена модель функции распределения электронной плотности для молекул NaOH и HCl на отрезке [0,30] Å (Рисунок 1).
При этом считалось, что длина ковалентной связи равна 1.5 Å, длина водородной связи равна 3.5 Å,
электронная плотность атомов описывается суммой гауссовых кривых,
максимум электронной плотности в центре атома пропорционален числу электронов в атоме.
Максимум электронной плотности в центре каждого атома был рассчитан,
как удвоенное число электронов в атоме: 22 для натрия, 16 для кислорода, 2 для водорода и 34 для хлора.
Модель функции распределения электронной плотности была построена скриптом compile-func.py командой:
python compile-func.py -g 22,3,3.5+16,3,5+2,3.5,6.5+2,3.5,10+34,3,11.5
Расчёт коэффициентов ряда Фурье
Функцию распределения электронной плотности можно разложить в ряд Фурье, рассчитав амплитуды и фазы.
Амплитуды и фазы для 0, 1, ..., 497, 498 гармоник ряда Фурье были рассчитаны скриптом func2fourier.py командой:
python func2fourier.py -i func.txt
Восстановление функции по рассчитанным коэффициентам
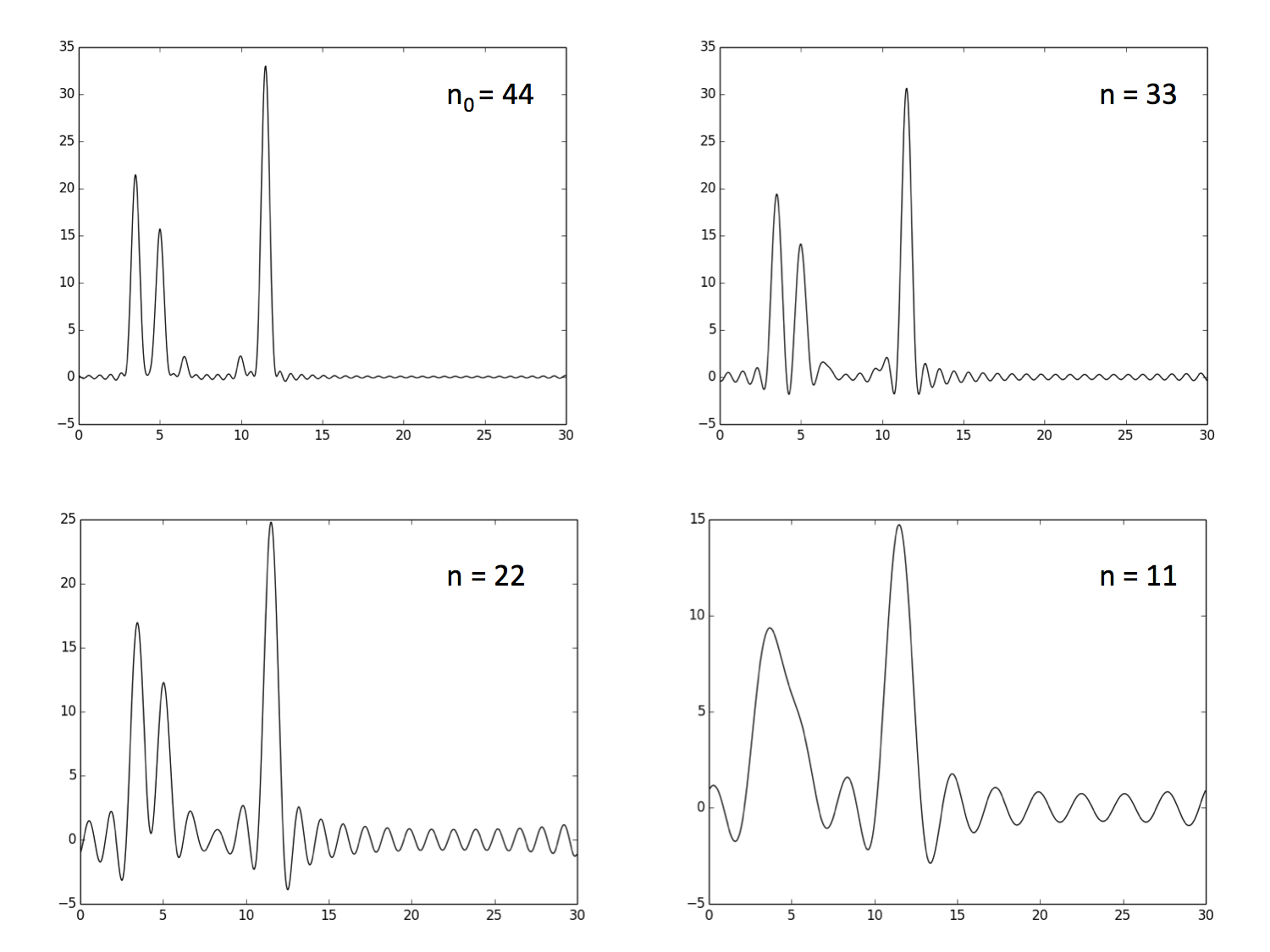
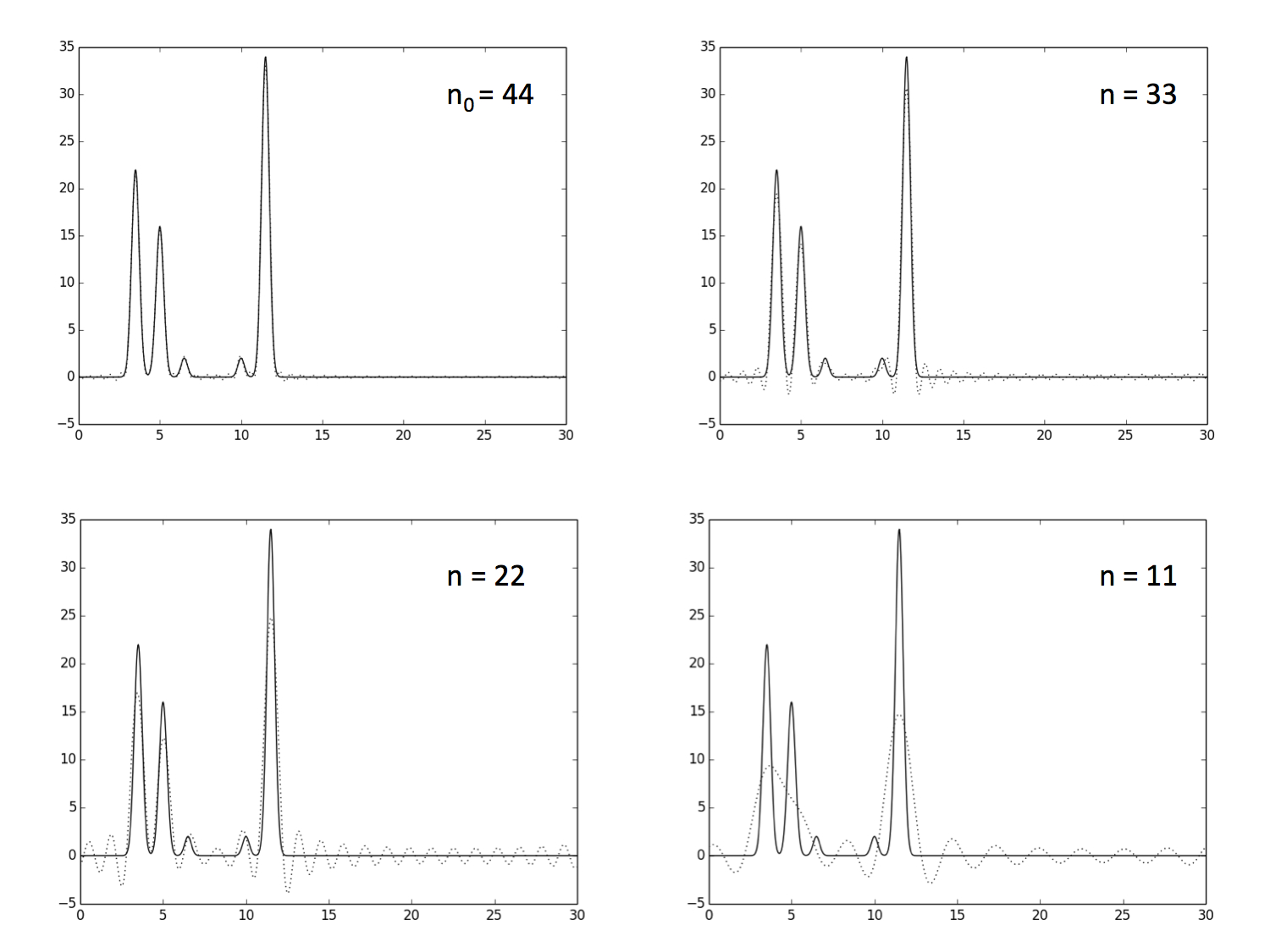
Восстановление функции по n0 = 44 коэффициентам ряда Фурье можно считать отличным
(можно определить положение максимумов всех гауссовых слагаемых функции).
Восстановление функции по n = 33 коэффициентам ряда Фурье можно считать хорошим,
хотя положение максимумов для атомов водорода определить уже сложнее.
Восстановление функции по n = 22 коэффициентам ряда Фурье можно считать средним,
поскольку положение максимумов для атомов натрия, кислорода и хлора определить всё ещё можно.
Восстановление функции по n = 11 коэффициентам ряда Фурье можно считать плохим (Рисунки 2 и 3).
Функция распределения электронной плотности была восстановлена скриптами fourier-filter.py и fourier2func.py командами:
python fourier-filter.py -r 0-n
python fourier2func.py -s
Добавление шума
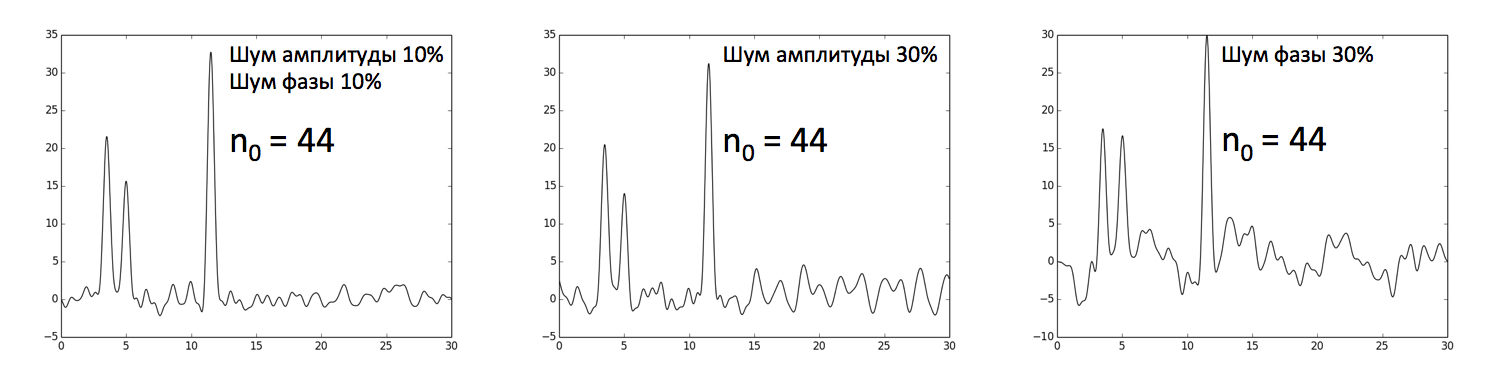
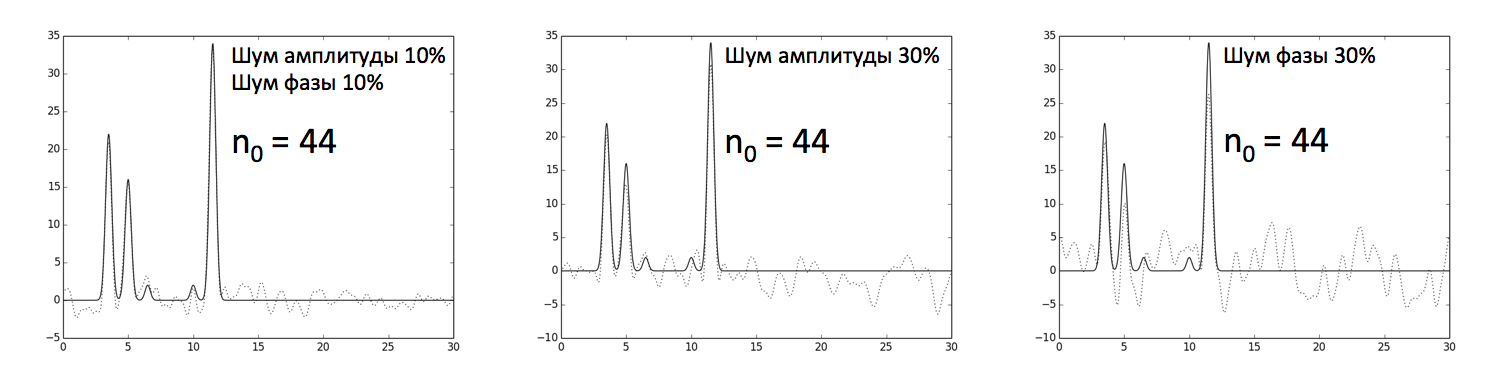
Для приближения модели к реальным условиям были рассчитаны амплитуды и фазы для 0, 1, ..., 497, 498 гармоник ряда Фурье с добавлением гауссового шума к амплитудам (30%), к фазам (30%), к амплитудам и фазам (по 10%). По рассчитанным n0 = 44 коэффициентам ряда Фурье была восстановлена функция распределения электронной плотности (Рисунки 4 и 5). В данном случае при добавлении различных шумов восстановление функции можно считать средним.
Неполные наборы гармоник
Для приближения модели к реальным условиям функция распределения электронной плотности была восстановлена по следующим наборам коэффициентов ряда Фурье
(коэффициенты были рассчитаны без добавления шума) (Рисунки 6 и 7):
• Исключены 0 и 1 гармоники ряда Фурье
• Исключены 21, 22, 23, 24 гармоники ряда Фурье
• Добавлена 55 гармоника ряда Фурье
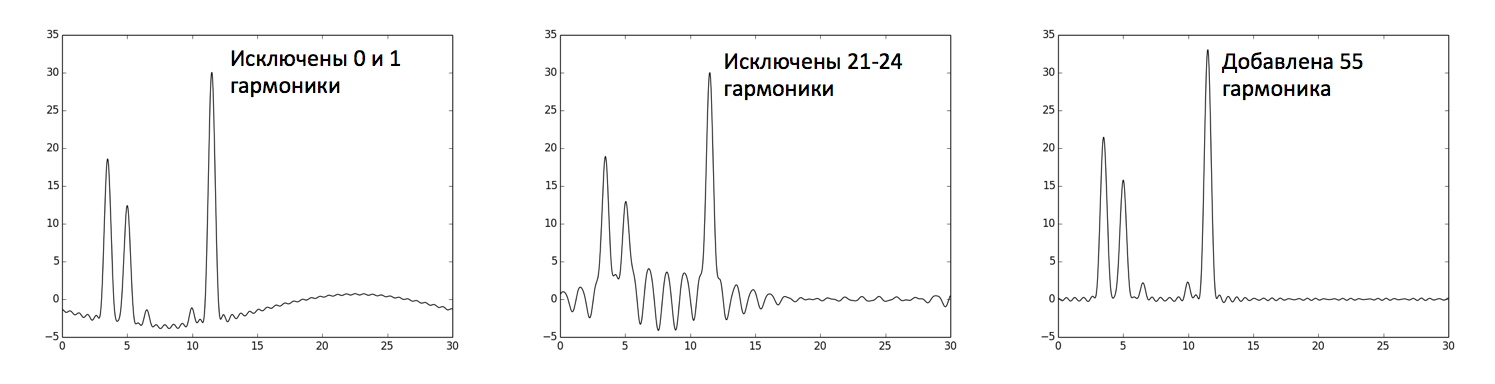
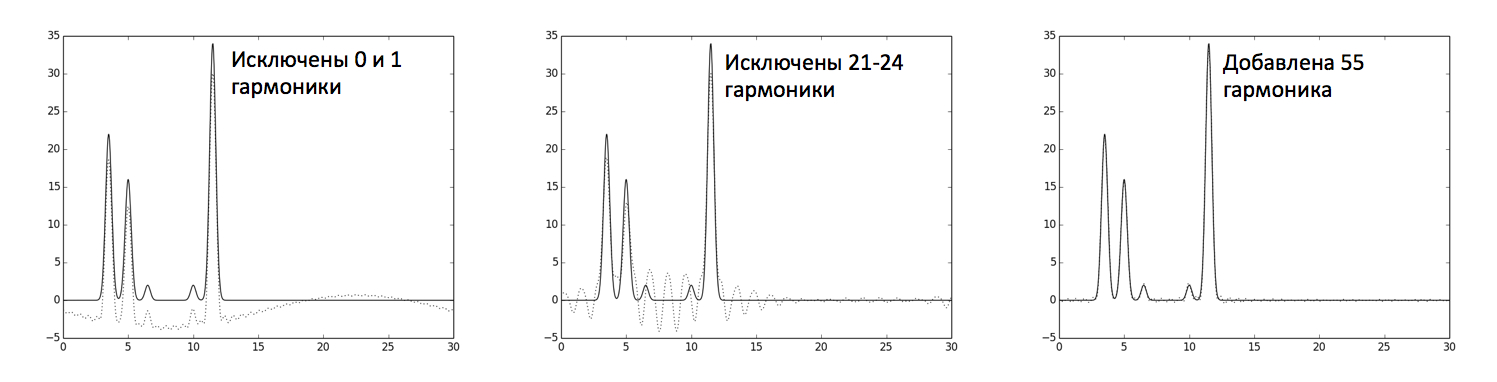
На рисунке 4 видно, что исключение небольшого числа (5%) начальных гармоник слабо влияет на качество восстановления функции. При исключении небольшого числа (10%) гармоник из середины набора восстановление функции можно считать средним. Добавление гармоник к полному набору, при котором восстановление функции отличное, должно только улучшать качество восстановления функции.
Набор гармоник ряда Фурье называется полным, если известны все гармоники с номерами 0, 1, …, n-1, n. Разрешением полного набора гармоник называют период (длину волны) гармоники с номером n. Пусть функция определена на отрезке длиной 30 Å. Тогда разрешение полного набора гармоник равно d = 30/n Å. Чем больше n, тем меньше d, тем выше разрешение, тем лучше восстановление функции.
Разрешение неполного набора гармоник можно рассчитывать по той же формуле, но в таком случае необходимо указывать полноту данных - процент гармоник, имеющих длину волны большую, чем гармоника с номером n. Для полного набора гармоник полнота данных равна 100%. Для набора гармоник, содержащего полный набор гармоник, при котором восстановление функции отличное, а также содержащего гармоники с меньшей длиной волны, полноту данных можно считать равной 100%.
Формально высокое разрешение при низкой полноте данных не гарантирует качественное восстановление функции.
| Таблица 1. Восстановление функции по коэффициентам ряда Фурье | |||||
| Полный набор гармоник | |||||
| Набор гармоник | Разрешение (Å) |
Полнота данных (%) |
Шум амплитуды (% от F) |
Шум фазы (% от φ) |
Качество восстановления |
| 0-11 | 2.73 | 100 | 0 | 0 | плохое |
| 0-22 | 1.36 | 100 | 0 | 0 | среднее |
| 0-33 | 0.91 | 100 | 0 | 0 | хорошее |
| 0-44 | 0.68 | 100 | 0 | 0 | отличное |
| 0-44 | 0.68 | 100 | 10 | 10 | среднее |
| 0-44 | 0.68 | 100 | 30 | 0 | среднее |
| 0-44 | 0.68 | 100 | 0 | 30 | среднее |
| Неполные наборы гармоник | |||||
| 2-44 | 0.68 | 95.6 | 0 | 0 | отличное |
| 0-20, 25-44 | 0.68 | 91.1 | 0 | 0 | среднее |
| 0-44, 55 | 0.68 | 100 | 0 | 0 | отличное |