| В качестве модели для компьютерного эксперимента была выбрана следующая модель: 2 молекулы, одна содержащая два атома, другая - четыре(2+4). |
| Атомы в каждой молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. |
| Далее была задана функция, моделирующаяся в 1D график электронной плотности молекулы, на интервале [0, 30] (интервал измеряется в ангстрем) при помощи compile-func.py |
| Гауссова функция определяется числами lambda,beta,gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2). |
| python compile-func.py -g 20,2,5+30,2,8+30.0,2,12+20.0,2,17+20.0,2,23+30,2,27. Max (gamma) расположены в точках 5,8,12,17,23,27, высота (lambda) 20, 30, 30, 20, 20, 30 соответственно; ширина "колокола" (beta) является порядка 1. |
| Ширина колокола (beta) примерно соответстветствует диаметру атома - чуть больше порядка 1 ангстрема (электронная плотность резко падает дальше), а высота (lambda) зависит от числа электронов в атоме. |
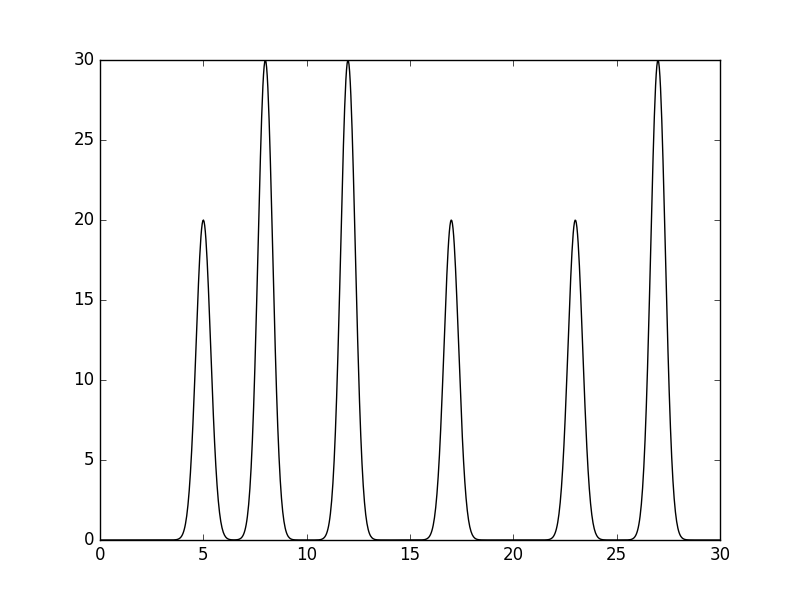 |
| Рис 1, график электронной плотности |
| Далее был произведен расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные. |
| Амплитуды и фазы были расчитаны по функции электронной плотности. При моделировании экспериментальных данных учитывается, что в эксперименте, во-первых, определяются амплитуды не для всех сигналов; во-вторых, интенсивности сигналов (следовательно, и амплитуды) |
| определяются с некой погрешностью; в-третьих, фазы определятся для всех измененных сигналов, но опять же с погрешностью. |
| Коэффициенты Фурье рассчитываются с помощью скрипта func2fourier.py |
| Входной файл – функция, полученная как выходной файл скрипта compile-func.py |
| python func2fourier.py -i func.txt |
| где Выходной файл имеет следующие данные: номер гармоники, амплитуда, фаза. |
| Далее был произведен отбор гармоник. |
| Набор гармоник ряда Фурье называется полным, если известны все гармоники с номерами 0, 1, 2, ...,n. Разрешением полного набора гармоник называется период гармоники с номером n, т.е. с наибольшим номером. |
| Период гармоники равен расстоянию между соседними максимумами синусоиды; его также называют длиной волны этой гармоники, хотя никакой физической волны нет. |
| Отбор гармоник проводили с помощью скрипта fourier-filter.py, который отбирает нужные строки. |
| Критерии оценки восстановления следующие: |
| Отличное восстановление – легко определить положение максимума всех атомов по графику восстановленной функции.
|
| Хорошее восстановление – можно предположить положения максимумов, зная число атомов, по восстановленной функции максимумы трудно отличить от шума. |
| Нормальное восстановление – есть атомы, положение которых определить по восстановленной функции нельзя, а есть те, у которых можно. |
| Плохое восстановление – положение атомов нельзя определить, можно только предсказать примерный размер "молекулы". |
| Далее была предпринята попытка восстановить функцию неполному набору гармоник с помощью fourier2func.py: |
| python fourier-filter.py -i func_ft.txt -r 0-5 -o func_ft0_5.txt. |
| python fourier2func.py -f func.txt -i func_ft0_5.txt -o 0_5.txt. |
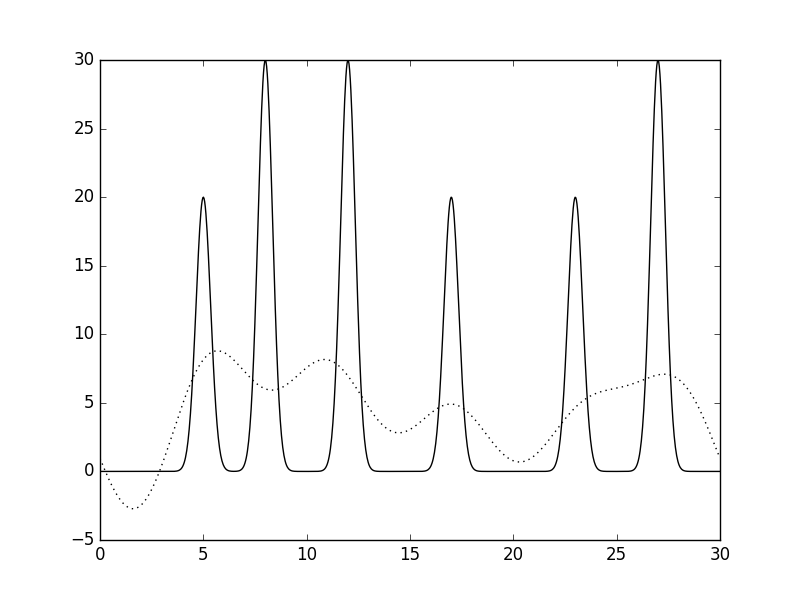 |
| Рис 2, восстановление функции по неполному набору гармоник (0-5). |
| Как видно из приведенного изображения, данное восстановление получилось плохим. |
| Далее были использованы друние параметры: |
| python fourier-filter.py -i func_ft.txt -r 0-10 -o func_ft0_10.txt. |
| python fourier2func.py -f func.txt -i func_ft0_10.txt -o 0_10.txt. |
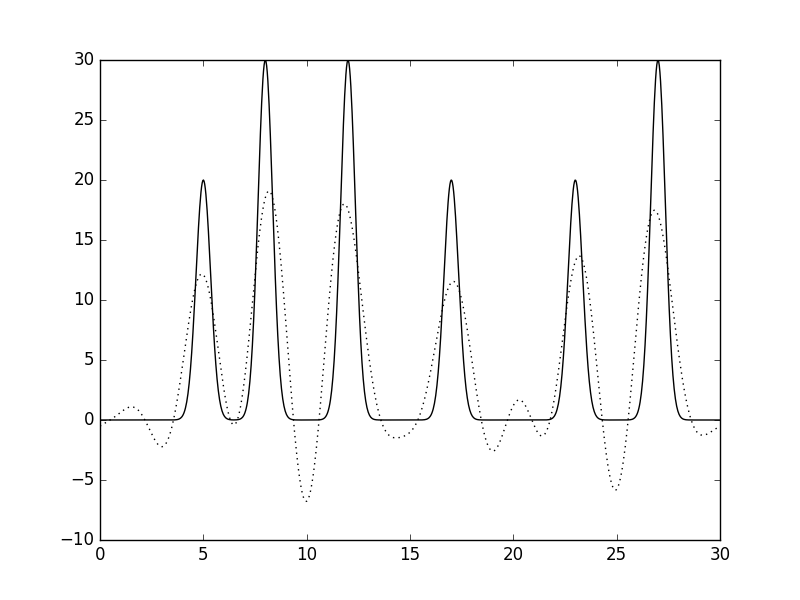 |
| Рис 3, восстановление функции по неполному набору гармоник (0-10). |
| Данное восстановление уже можно считать нормальным. |
| python fourier-filter.py -i func_ft.txt -r 0-25 -o func_ft0_25.txt. |
| python fourier2func.py -f func.txt -i func_ft0_25.txt -o 0_25.txt. |
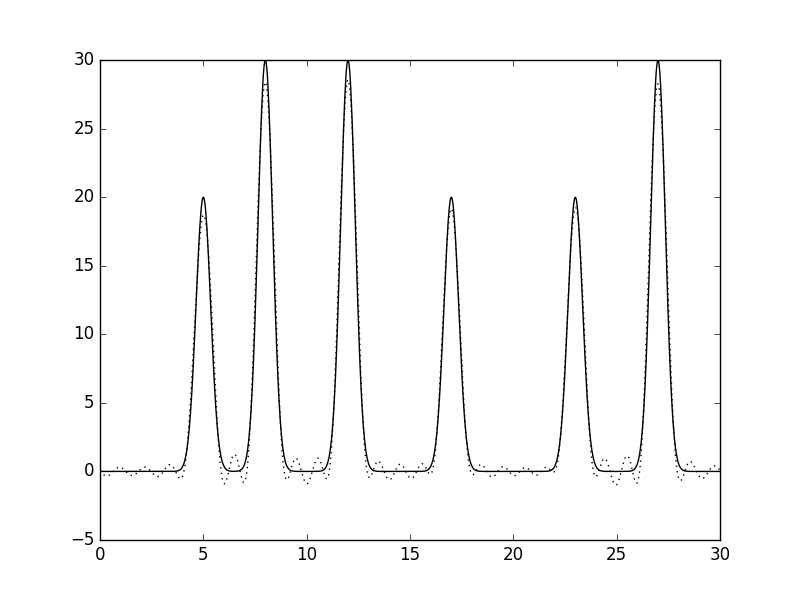 |
| Рис 6, восстановление функции по неполному набору гармоник (0-25). |
| Данное восстановление уже будет являться отличным. |
| Таким образом, уже восстановлении функции по гармоникам 0-25 качество отличное, поэтому минимальное число гармоник, при котором у функции отличное восстановление: 25 - n0 |
| Добавление шума к амплитуде (F) или/и к фазе (P) |
| При восстановлении функции по первым 25 гармоникам было добавлено 10%, 15% и 25% шума к амплитудам и фазам отдельно. |
| Добавление 10% шума к амплитуде: |
| python func2fourier.py -F 10 -P 0 -i func.txt -o n_f10p0.txt |
| python fourier-filter.py -r 0-25 -i n_f10p0.txt -o n_f10p0_25.txt |
| python fourier2func.py -i n_f10p0_25.txt -o func_n_f10p0_25.txt |
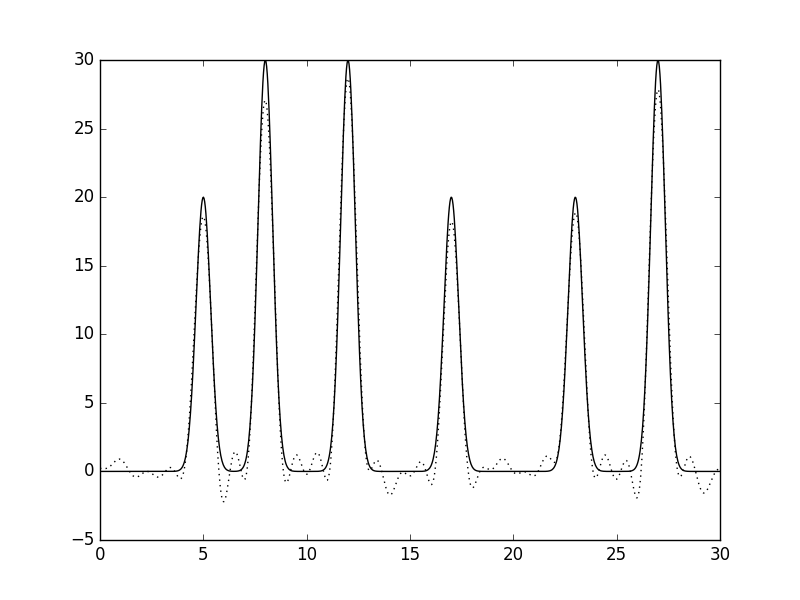 |
| Рис 8, восстановление функции по неполному набору гармоник (0-25)при добавлении 10% шума к амплитуде. |
| Добавление 15% шума к амплитуде: |
| python func2fourier.py -F 15 -P 0 -i func.txt -o n_f15p0.txt |
| python fourier-filter.py -r 0-25 -i n_f15p0.txt -o n_f15p0_25.txt |
| python fourier2func.py -i n_f15p0_25.txt -o func_n_f15p0_25.txt |
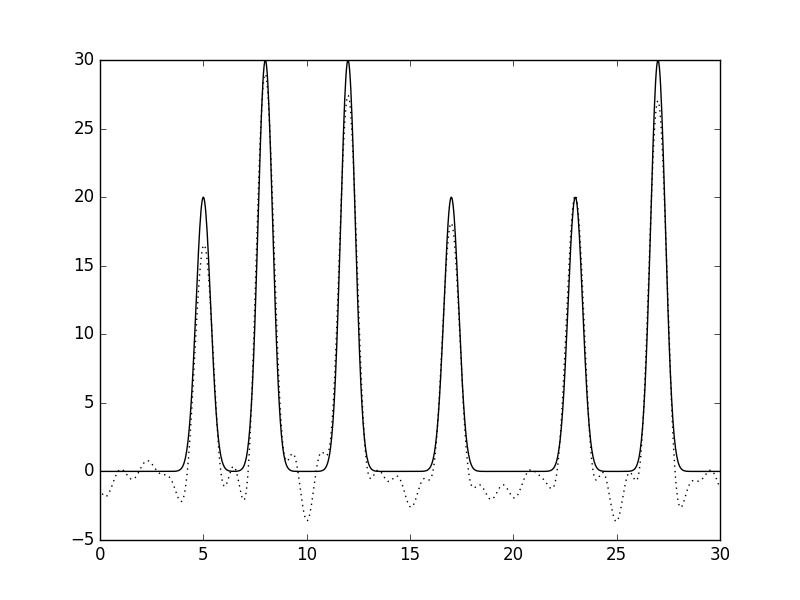 |
| Рис 9, восстановление функции по неполному набору гармоник (0-25)при добавлении 15% шума к амплитуде. |
| Добавление 25% шума к амплитуде: |
| python func2fourier.py -F 25 -P 0 -i func.txt -o n_f25p0.txt |
| python fourier-filter.py -r 0-25 -i n_f25p0.txt -o n_f25p0_25.txt |
| python fourier2func.py -i n_f25p0_25.txt -o func_n_f25p0_25.txt |
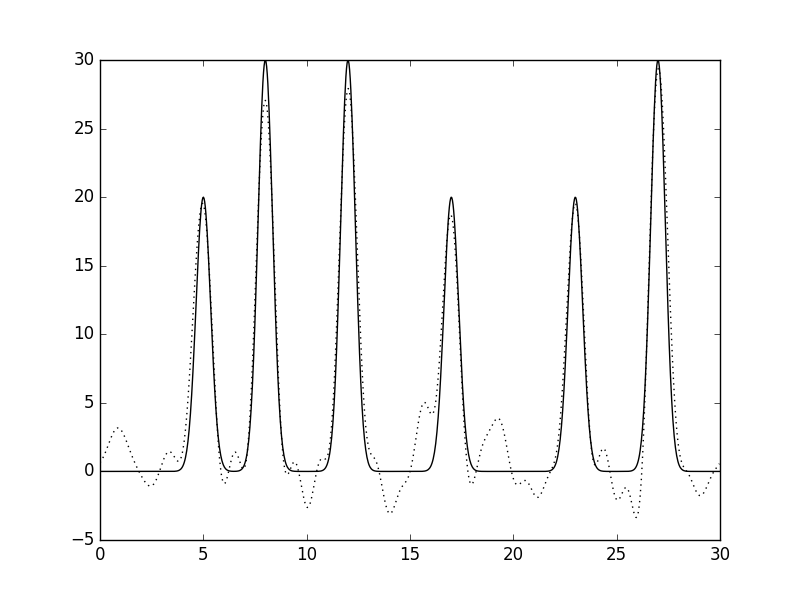 |
| Рис 10, восстановление функции по неполному набору гармоник (0-25)при добавлении 25% шума к амплитуде. |
| Добавление 10% шума к фазам: |
| python func2fourier.py -F 0 -P 10 -i func.txt -o no_f0p10.txt |
| python fourier-filter.py -r 0-25 -i no_f0p10.txt -o no_f0p10_25.txt |
| python fourier2func.py -i no_f0p10_25.txt -o func_no_f0p10_25.txt |
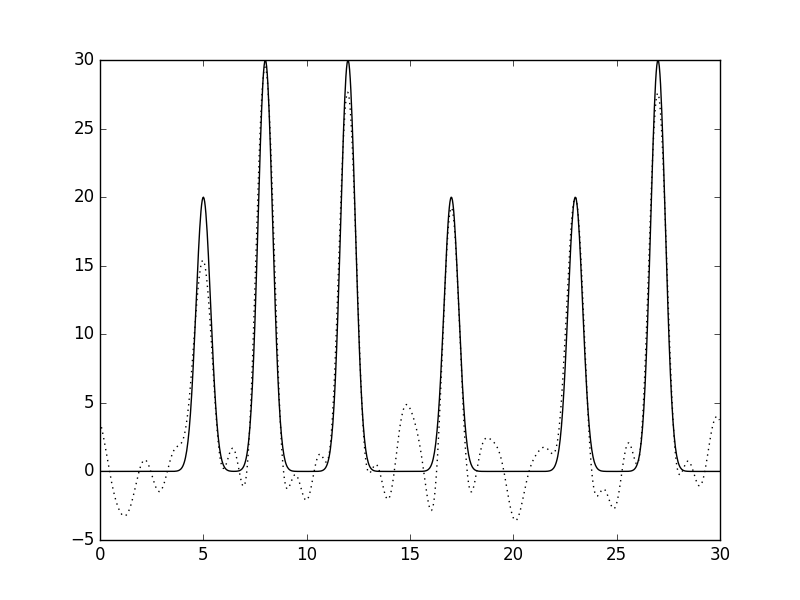 |
| Рис 11, восстановление функции по неполному набору гармоник (0-25)при добавлении 10% шума к фазам. |
| Добавление 15% шума к фазам: |
| python func2fourier.py -F 0 -P 15 -i func.txt -o no_f0p15.txt |
| python fourier-filter.py -r 0-25 -i no_f0p15.txt -o no_f0p15_25.txt |
| python fourier2func.py -i no_f0p15_25.txt -o func_no_f0p15_25.txt |
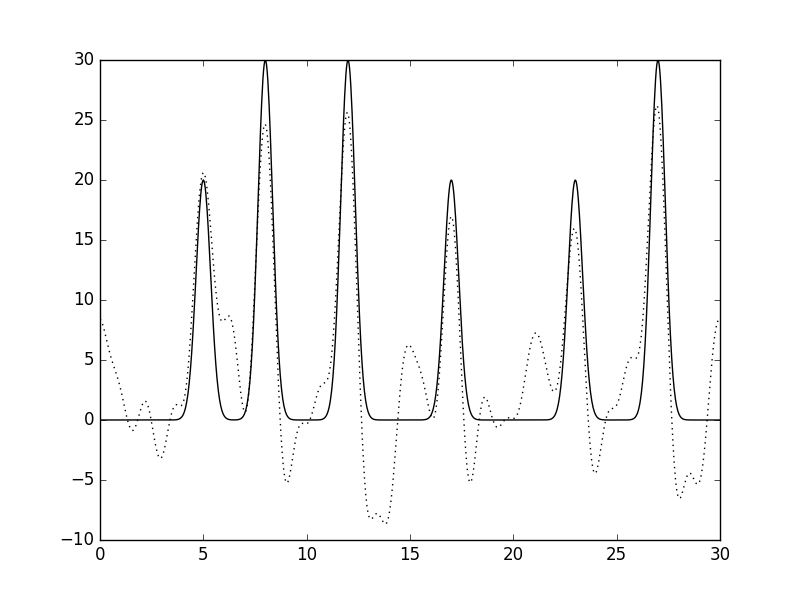 |
| Рис 12, восстановление функции по неполному набору гармоник (0-25)при добавлении 15% шума к фазам. |
| Добавление 25% шума к фазам: |
| python func2fourier.py -F 0 -P 25 -i func.txt -o no_f0p25.txt |
| python fourier-filter.py -r 0-25 -i no_f0p25.txt -o no_f0p25_25.txt |
| python fourier2func.py -i no_f0p25_25.txt -o func_no_f0p25_25.txt |
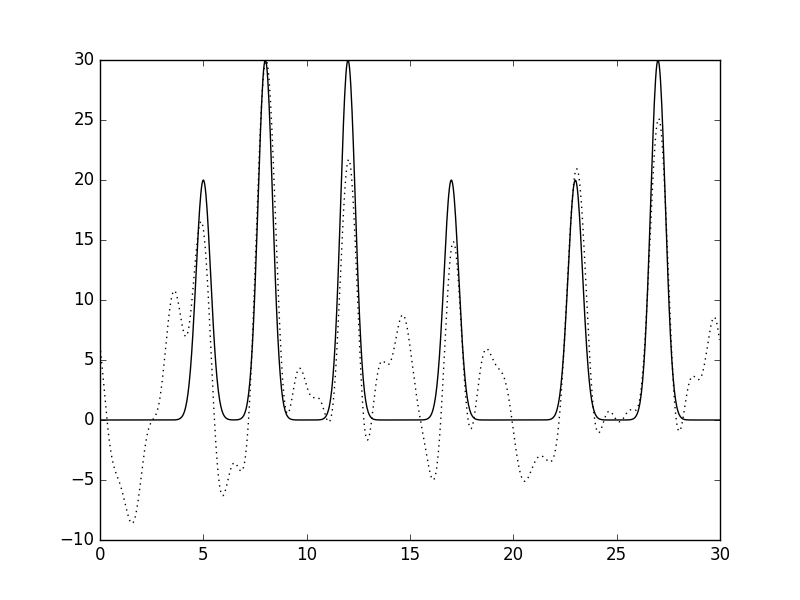 |
| Рис 13, восстановление функции по неполному набору гармоник (0-25)при добавлении 25% шума к фазам. |
| Можно сделать вывод, что шум в фазах вносит намного больший вклад в изменения, чем шум в амплитудах. |
| Добавление 10% и 25% шума к амплитудам и фазам одновременно: |
| Добавление 10% шума к амплитудам и фазам одновременно: |
| python func2fourier.py -F 10 -P 10 -i func.txt -o noise_f10p10.txt |
| python fourier-filter.py -r 0-25 -i noise_f10p10.txt -o noise_f10p10_25.txt |
| python fourier2func.py -i noise_f10p10_25.txt -o func_noise_f10p10_25.txt |
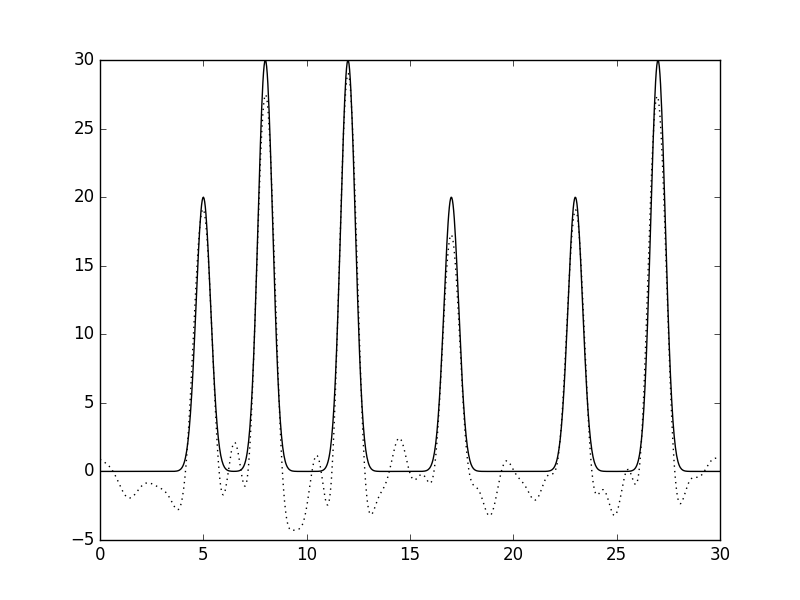 |
| Рис 14, восстановление функции по неполному набору гармоник (0-25)при добавлении 10% шума к амплитудам и фазам одновременно |
| Добавление 25% шума к амплитудам и фазам одновременно: |
| python func2fourier.py -F 25 -P 25 -i func.txt -o noise_f25p25.txt |
| python fourier-filter.py -r 0-25 -i noise_f25p25.txt -o noise_f25p25_25.txt |
| python fourier2func.py -i noise_f25p25_25.txt -o func_noise_f25p25_25.txt |
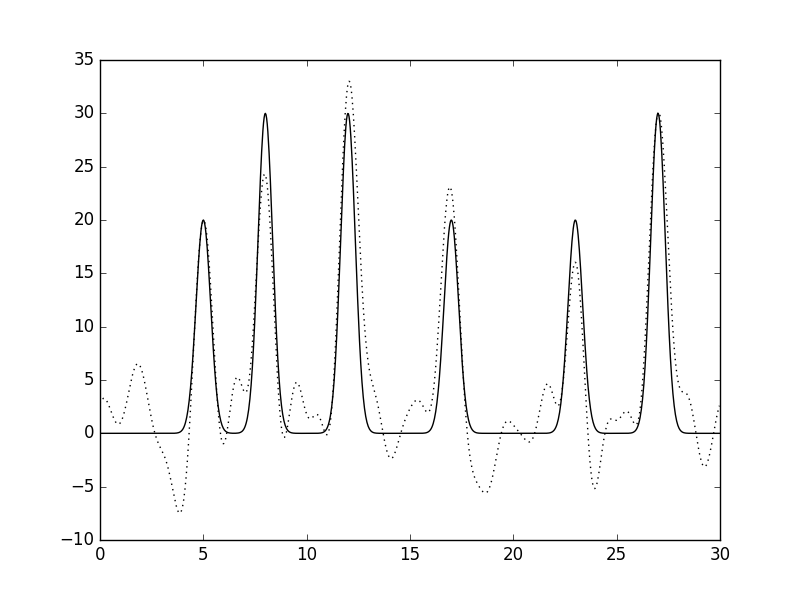 |
| Рис 15, восстановление функции по неполному набору гармоник (0-25)при добавлении 25% шума к амплитудам и фазам одновременно. |
| При добавлении 10% шума к амплитудам и фазам одновременно, качество восстановления становится хорошим, а при добавлении 25% шума - качество становится плохим. |
<| Далее были расмотрены неполных гармоники. |
| Для начала удалим 0 гармонику: |
| python fourier-filter.py -i func_ft.txt -r 1-25 -o func_ft1_25.txt. |
| python fourier2func.py -f func.txt -i func_ft1_25.txt -o 1_25.txt. |
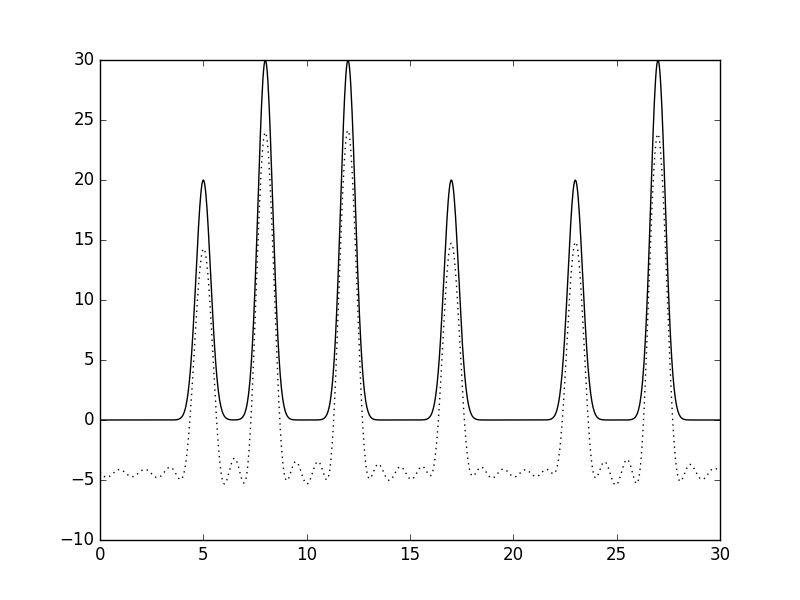 |
| Рис 16, восстановление функции по неполному набору гармоник (1-25). |
| Как можно хаметить, удаление 0 гармоники приводит к смещению функции вниз. |
| Теперь удалим 1-3 гармоники: |
| python fourier-filter.py -i func_ft.txt -r 4-25 -o func_ft4_25.txt. |
| python fourier2func.py -f func.txt -i func_ft4_25.txt -o 4_25.txt. |
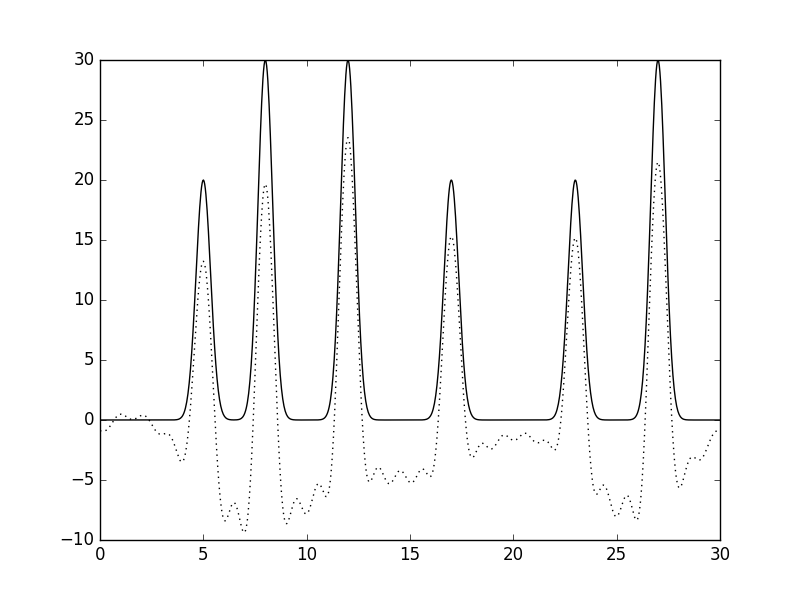 |
| Рис 17, восстановление функции по неполному набору гармоник (4-25). |
| Как можно заметить, удаление 1-3 гармоник приводит к наибольшему искривлению амплитуды, смещенной вниз. |



























