Учебный сайт Полины Байкузиной

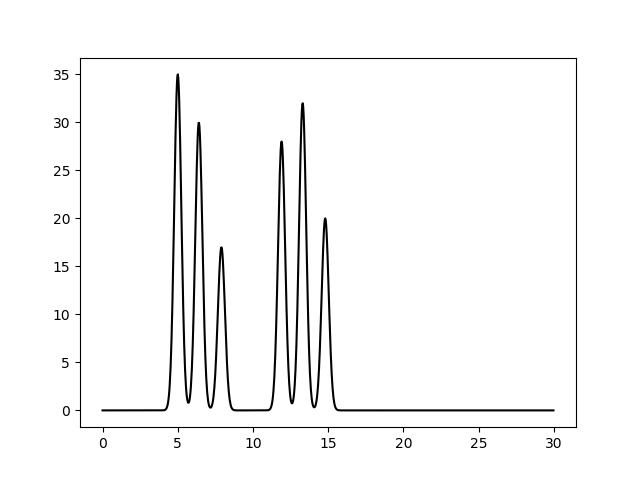
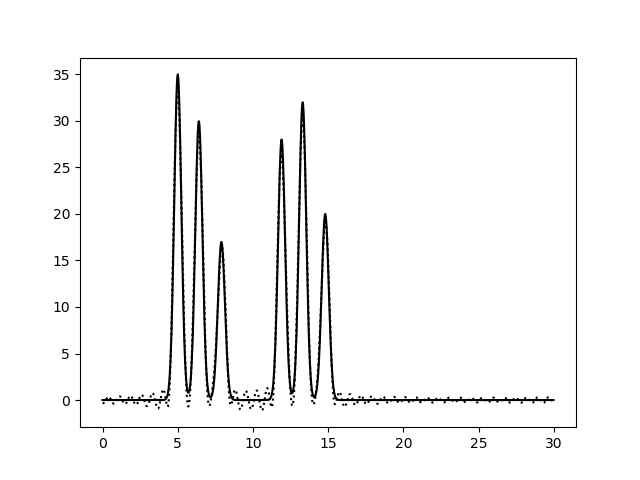
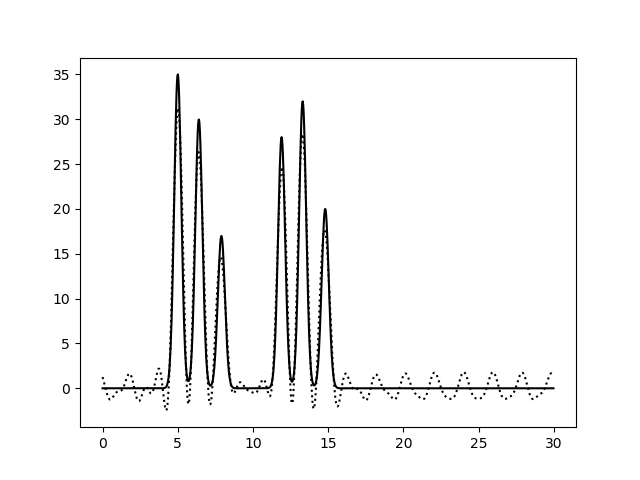
Разложение функции в ряд Фурье

Была смоделирована функция электронной плотности в одномерной элементарной ячейке на отрезке [0,30]. Модель представляет собой две молекулы, расположенные на расстоянии около 4Å друг от друга. Молекулы состоят из 3 атомов, расстояние между атомами 1 -1,5Å.

Функция была получена с помощью скрипта compile-func.py (использует модуль fourier) с параметрами 35,3,5+30,3,6.4+17,3,7.9+28,3,11.9+32,3,13.3+20,3,14.8 (сумма шести гауссовых функций с максимумами в точках 5, 6.4, 7.9, 11.9, 13.3, 14.8 и высотой пиков 35, 30, 17, 28, 32, 20, соответственно).

Полученная функция представлена на рисунке 1.

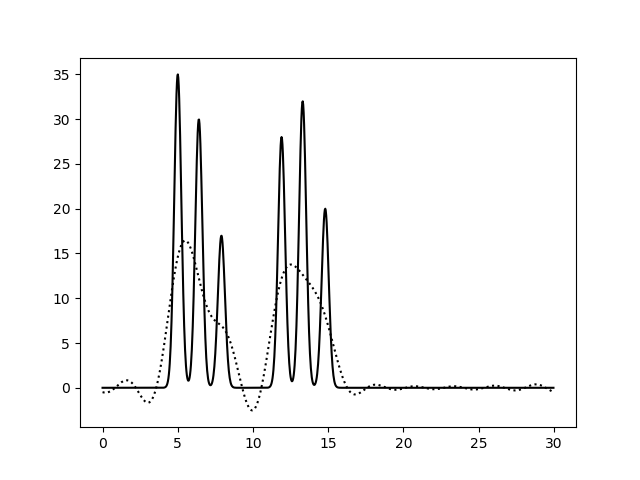
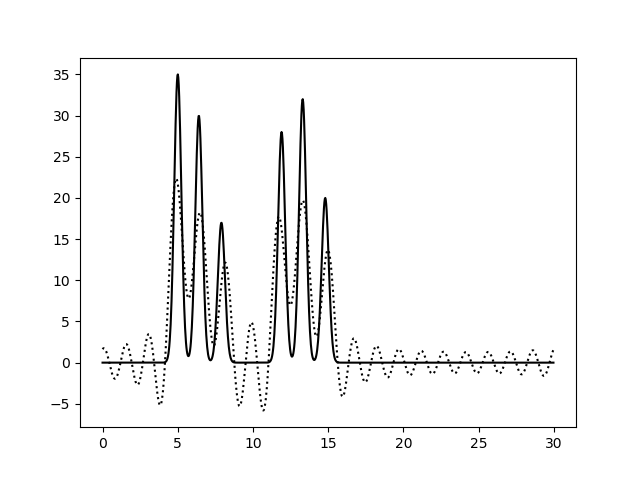
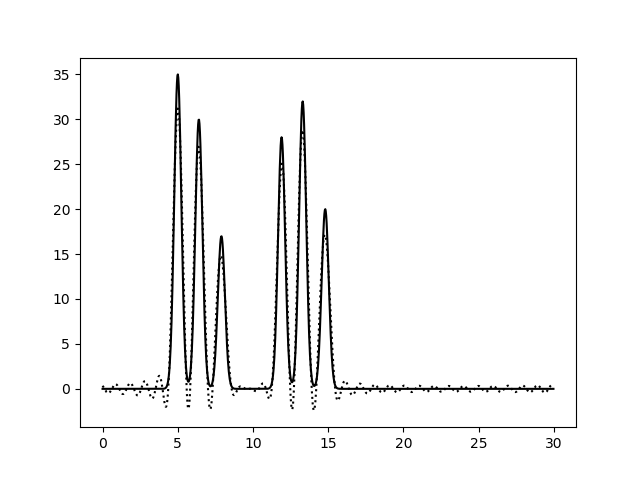
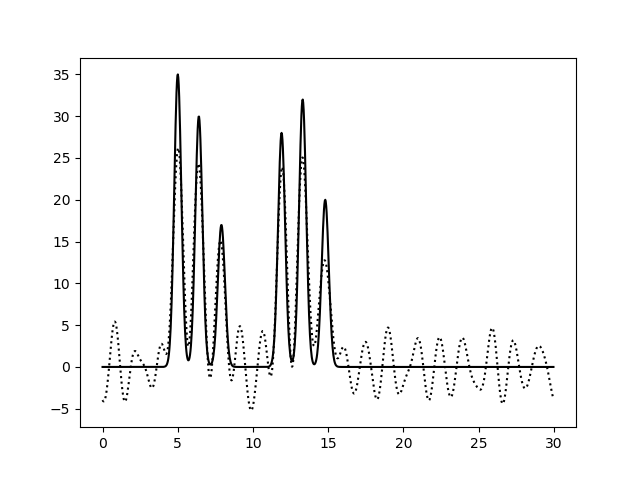
Коэффициенты Фурье были рассчитаны с помощью скрипта func2fourier.py (на вход подается функция, полученная как выходной файл скрипта compile-func.py). Полученный файл содержал 498 гармоник из разложения функции ЭП в ряд Фурье.

Затем было подобрано такое количество гармоник, по которым качество восстановления можно считать отличным (по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции). Для восстановления функции электронной плотности по набору гармоник был использован скрипт fourier2func.py. Полученные графики приведены на рисунках 2 и 3.

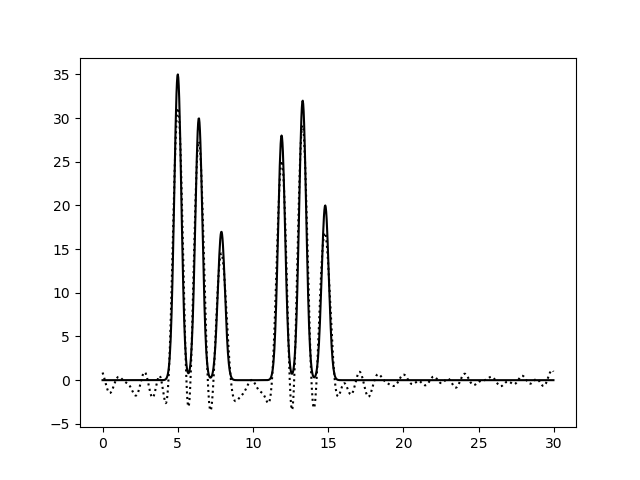
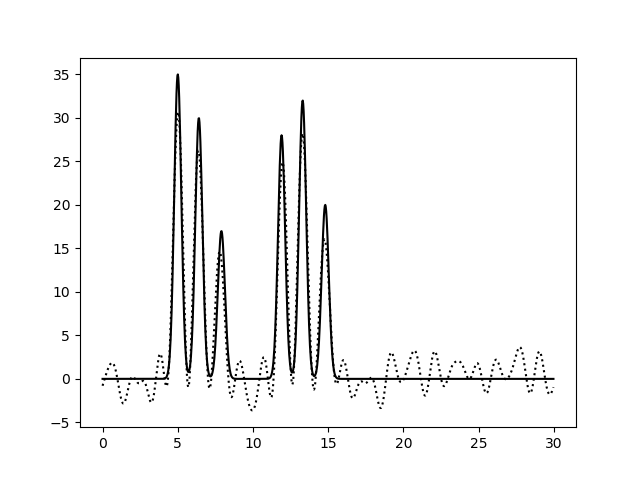
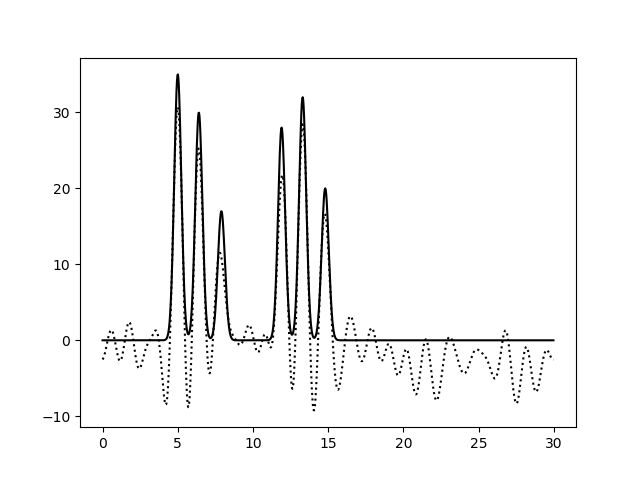
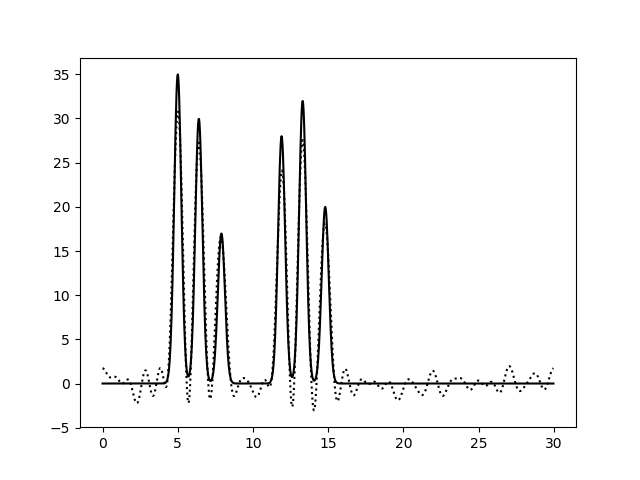
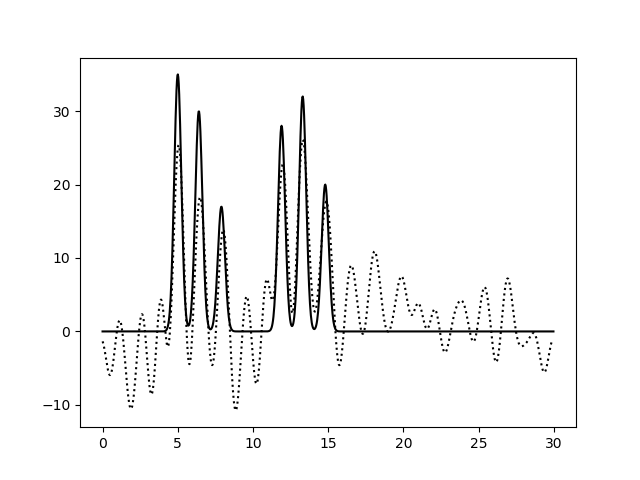
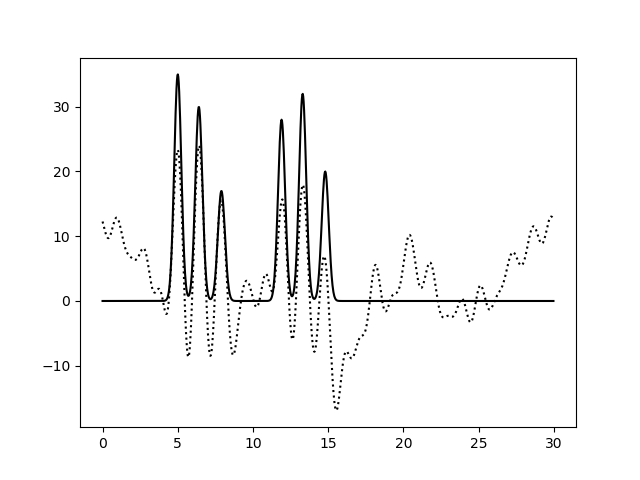
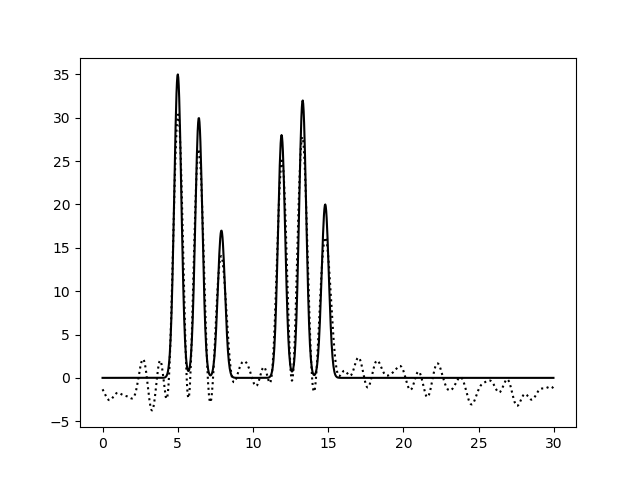
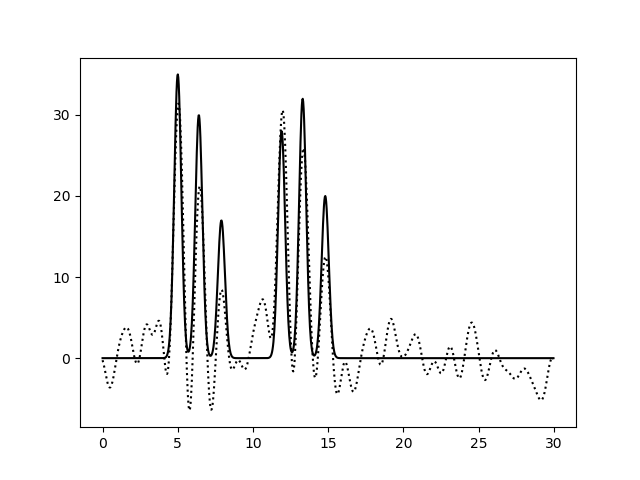
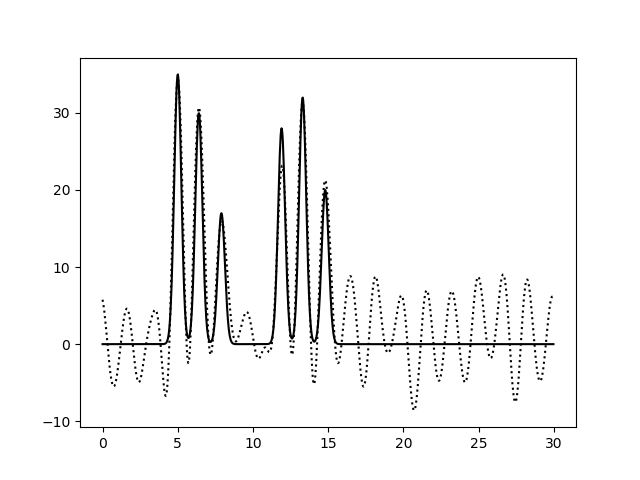
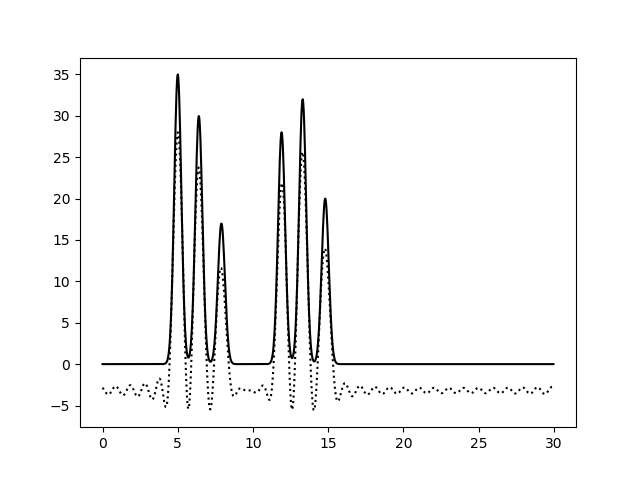
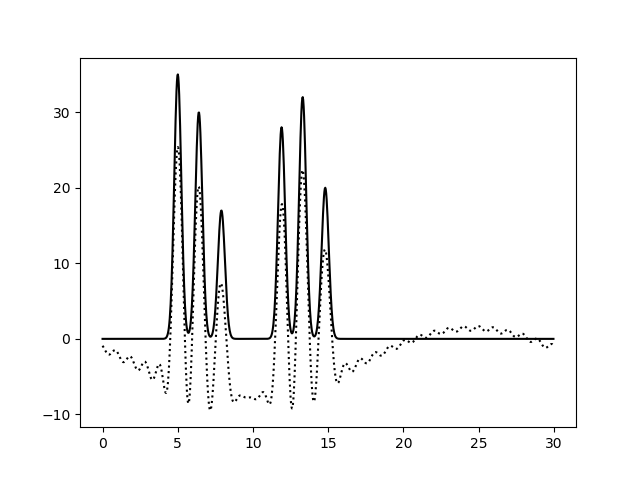
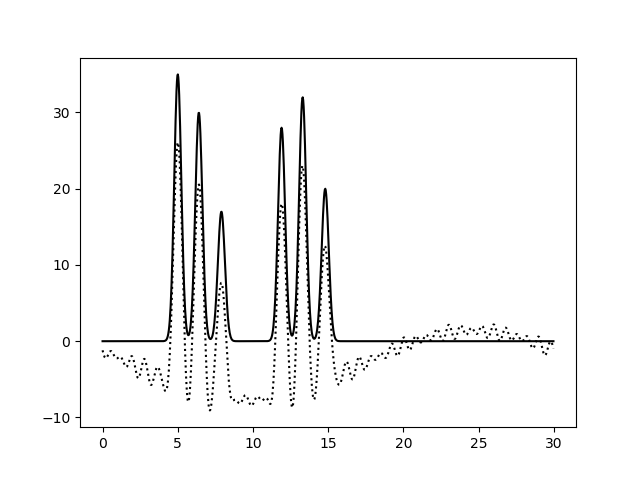
При восстановлении функции ЭП по набору гармоник 0-10 можно только предсказать примерный размер молекул, положение атом определить невозможно. По набору гармоник 0-20 можно определить положение отдельных атомов, но значения максимумов функции не совпадают с исходными. Восстановление по гармоникам 0-30 отличное, положения атомов определяются точно, высота пиков совпадает. Далее все операции проводились с набором гармоник 0-30.

Далее было проанализировано влияние шума на качество восстановления функции ЭП (рис.4-6). При увеличении шума по амплитуде качество восстановление практически не меняется, пики атомов хорошо различимы. При увеличении шума по фазе качество заметно ухудшается, положение не всех атомов устанавливается однозначно.

Затем было проанализировано восстановление функции электронной плотности по неполным наборам гармоник, так как в РСА эксперименте не удается получить полный набор гармоник.

На рисунке 7 приведены графики функции ЭП по наборам гармоник 1-30 и 2-30. Качество восстановления остается отличным, положения атомов определяются довольно точно, несмотря на то что график смещается относительно оси OX. При удалении 2 гармоник подряд из середины набора незначительно увеличивается шум, но высота и положение пиков не меняется (рис.8, слева). При удалении 3 гармоник (10%) из разных мест набора качество ухудшается, возрастает шум, при наличии в модели легких атомов было бы сложно определить реальное положение атомов (рис.8, в центре). При добавлении гармоники с номером, превышающим n_0 на 10 (в данном случае 40), картина практически не изменилась (рис.7 и рис.8, справа).

В таблице 1 приведена информация о восстановлении функции электронной плотности по разным наборам гармоник. Разрешением полного набора гармоник называется период гармоники с номером n, то есть с наибольшим номером. Период гармоники равен расстоянию между соседними максимумами синусоиды и вычисляется по формуле d=T/n, где T - длина рассматриваемого отрезка (в нашем случае 30), n - номер гармоники. Для неполного набора данных кроме разрешения d необходимо сообщить полноту данных — процент гармоник с длиной волны большей d от максимально возможного, присутствующих в наборе.