Цель и задачи
Цель данной работы заключается в исследовании качества восстановления функции ЭП от одной переменной в зависимости от того, какие и сколько гармоник ряда Фурье используются для ее восстановления.
Задание включает следующие этапы:
- Создание модельной функции ЭП в одномерной элементарной ячейке;
- Расчет параметров сигнала, моделирующих экспериментальные данные: амплитуды и фазы;
- Восстановление функции ЭП по модельным ("экспериментальным") данным;
- Оценка качества восстановления функции ЭП.
Создание модели и задание функции
Для начала было создана линейная атомная модель, изображенная на риснке 1. Следует понимать, что это гипотетическая модель, а из-за линейности здесь не могут учитываться валентные углы. Но тем не менее, длина водородных и ковалентных связей, Ван-дер-Ваальсовы радиусы атомов в молеклах модели приближены к их прототипам:
- синильная кислота (HCN);
- вода(H2O),
- фрагмент гидрофосфата (HPO42-).
Протяженность модели составляет 14,98Å.
 |
Далее на основе этой модели на интервале [0 Å, 30 Å] была задана функция, описывающая одномерную электронную плотность. Функция имеет вид нескольких гауссовых кривых с центром в разных точках и определяется числами lambda, beta, gamma по формуле:
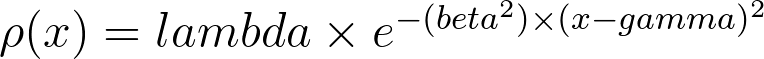
lambda - высота гауссовской кривой, соответствующая максимуму электронной плотности в центре атома. Это значение задавалось так, чтобы было пропорционально числу электронов в атоме:
- H - 2;
- C - 24;
- N - 28;
- O - 32;
- P - 64.
beta - ширина "колокола", которая примерно соответствует диаметру атома:
- H - 2.1 Å;
- C - 3.4 Å;
- N - 3.1 Å;
- O - 3.04 Å;
- P - 3.6 Å.
gamma - координата максимума гауссовой кривой, соответстующая центру атома. Координаты центров атомов на оси x:
- HHCN – 7
- CHCN – 8.06
- NHCN – 9.22
- HH2O – 13.06
- OH2O – 14.02
- HH2O – 14.98
- OHPO42- – 16.97
- PHPO42- – 18.49
- OHPO42- – 19.99
- HHPO42- – 20.94
Функция была задана с помощью скрипта compile-func.py командой:
python compile-func.py -g
2,2.1,7+24,3.4,8.06+28,3.1,9.22+2,2.1,13.06+32,3.04,14.02+2,2.1,14.98+32,3.04,16.97+
64,3.6,18.49+32,3.04,19.99+2,2.1,20.94График электронной плотности модели атомов представлен на рисунке 2.
Поточенчные координаты приведены в файле func.txt.
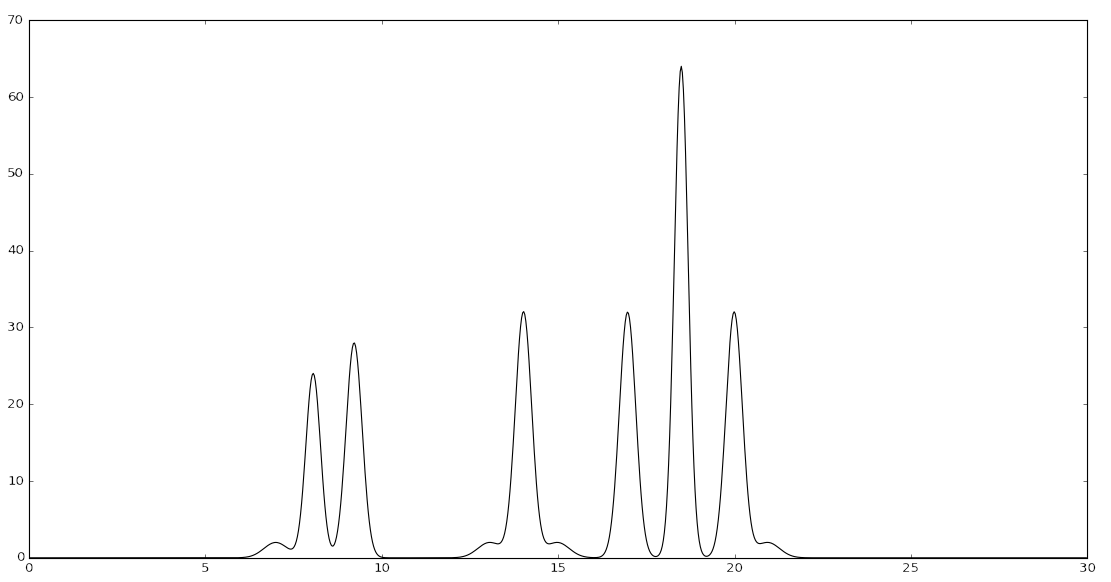 Рисунок 2. График электронной плотности линейной модели атомов.
Рисунок 2. График электронной плотности линейной модели атомов.
Расчёт коэффициентов Фурье
Коэффициенты разложения функции в ряд Фурье были получены с помощью скрипта func2fourier.py командой:
python func2fourier.py -i func.txt
Скрипт раскладывает полученный ранее файл func.txt на 499 гармоник на отрезке [0 Å, 30 Å]. Выходной файл скрипта – файл func_ft.txt.
Восстановление функции электронной плотности по амплитудам и фазам
Полные наборы гармоник
По полному набору гармоник был построен график восстановленной функции электронной плотности модели с помощью скрипта fourier2func.py командой:
python fourier2func.py -f func.txt -i func_ft.txt -sГрафик восстановленной функции, (рис.3) идентичен графику первоначальной функции (рис.1):
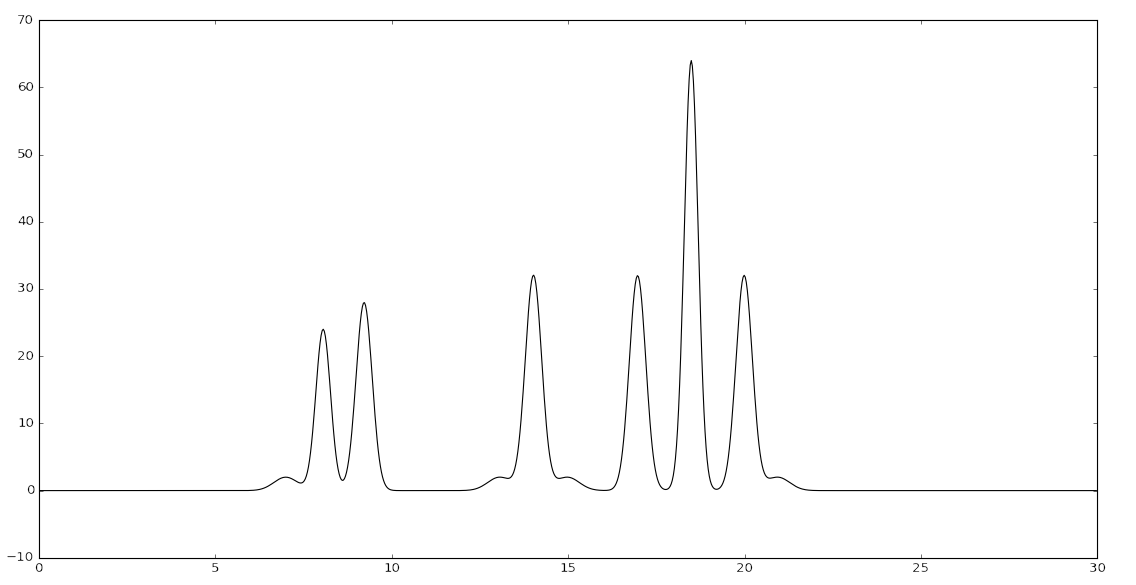 Рисунок 3. График восстановленной функции электронной плотности
Рисунок 3. График восстановленной функции электронной плотности
Очевидно, что при количестве гармоник, равном 499, получается отличное восстановление, т.е. по графику восстановленной функции можно определить положение максимумов всех гауссовых слагаемых. При таком количестве гармоник разрешение составляет 0.06 Å. Это довольно высокое значение. Например, в ренгеноструктурном эксперименте разрешение ниже на два порядка.
Далее с помощью уже знакомого скрипта fourier2func.py и fourier-filter.py, который производит отбор гармоник, был произведен поиск минимального числа гармоник, при котором восстановление функции сохранится отличным:
fourier-filter.py -r 0-1 -i func_ft.txt -o ffr_1.txt
fourier2func.py -f func.txt -i ffr_1.txt -o ffc_1.txt
fourier-filter.py -r 0-10 -i func_ft.txt -o ffr_10.txt
fourier2func.py -f func.txt -i ffr_10.txt -o ffc_10.txt
fourier-filter.py -r 0-20 -i func_ft.txt -o ffr_20.txt
fourier2func.py -f func.txt -i ffr_20.txt -o ffc_20.txt
fourier-filter.py -r 0-25 -i func_ft.txt -o ffr_25.txt
fourier2func.py -f func.txt -i ffr_25.txt -o ffc_25.txt
fourier-filter.py -r 0-30 -i func_ft.txt -o ffr_30.txt
fourier2func.py -f func.txt -i ffr_30.txt -o ffc_30.txt
fourier-filter.py -r 0-40 -i func_ft.txt -o ffr_40.txt
fourier2func.py -f func.txt -i ffr_40.txt -o ffc_40.txt
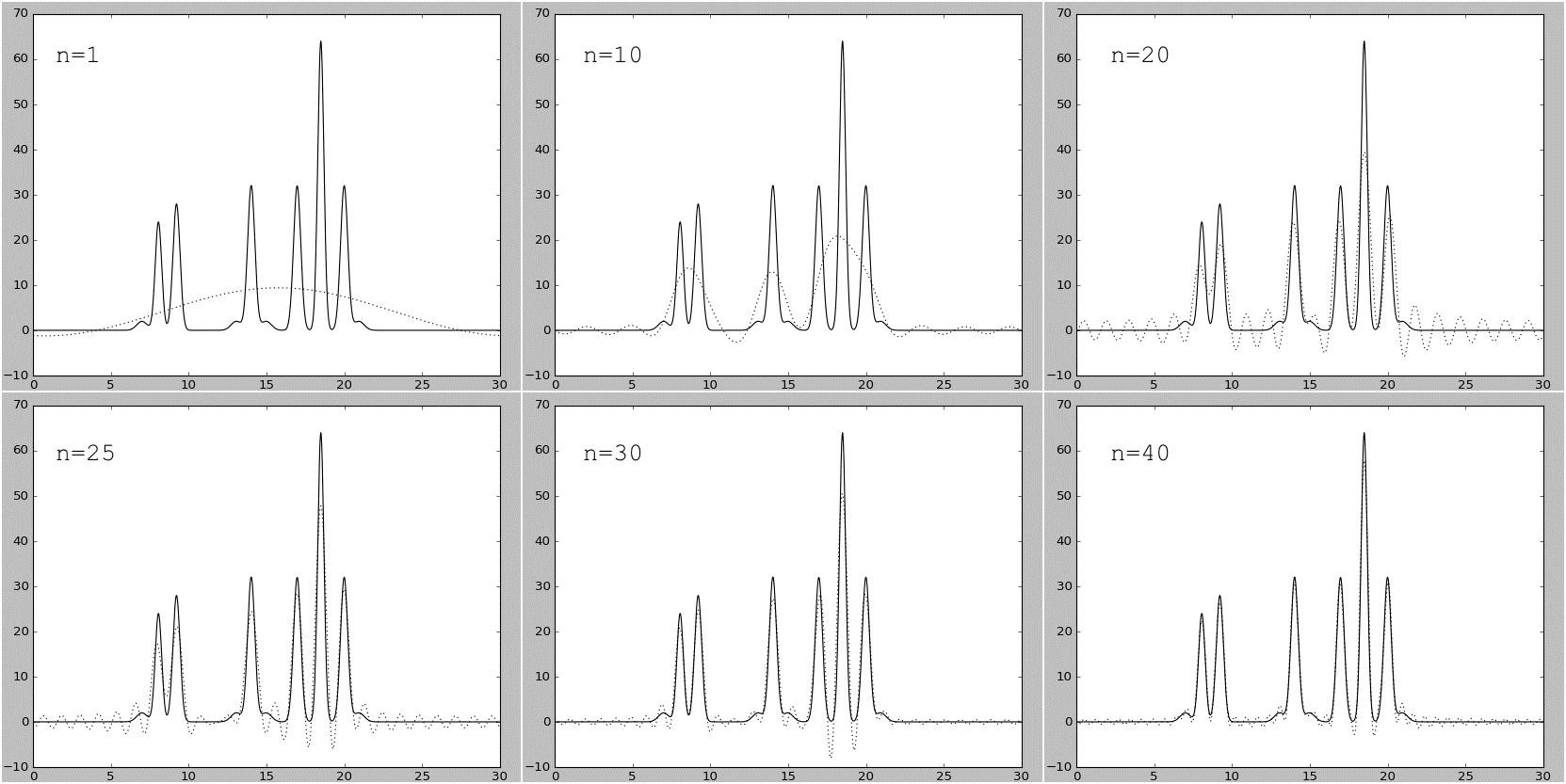 Рисунок 4.Графики восстановленных функций, представленные пунктирной линией, для
1, 10, 20, 25, 30 и 40 гармоник. Исходная функция – представлена в виде сплошной линии.
Рисунок 4.Графики восстановленных функций, представленные пунктирной линией, для
1, 10, 20, 25, 30 и 40 гармоник. Исходная функция – представлена в виде сплошной линии.
Как сравнить восстановленную функцию с исходной?
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов");
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума;
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно;4
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".
Исходя из графиков, определяется, что 41 - это минимальное число гармоник, при котором функция сохраняет отличное восстановление.
- Для n = 2, n = 11 – плохое восстановление;
- Для n = 21 – среднее восстановление;
- Для n = 26, n = 31 – хорошее восстановление;
- Для n = 41 – отличное восстановление.
Затем при восстановлении по полному набору гармоник 0,...,40 был добавлен шум:
- 10% к амплитуде; 10% к фазе; по 5% к амплитуде и фазе (рис.5)
- 20% к амплитуде; 20% к фазе; по 10% к амплитуде и фазе (рис.6)
- 50% к амплитуде; 50% к фазе; по 25% к амплитуде и фазе (рис.7)
Были использованы следующие команды (показан только вариант с параметрами шума 10% к амплитуде; 10% к фазе; по 5% к амплитуде и фазе):
Добавление шума только к амплитуде
python func2fourier.py -F 10 -i func.txt -o ft_noise_f10.txt
python fourier-filter.py -r 0-40 -i ft_noise_f10.txt -o ft_noise_f10_40.txt
python fourier2func.py -i ft_noise_f10_40.txt -o func_noise_f10_40.txt
Добавление шума только к фазе
python func2fourier.py -P 10 -i func.txt -o ft_noise_p10.txt
python fourier-filter.py -r 0-40 -i ft_noise_p10.txt -o ft_noise_p10_40.txt
python fourier2func.py -i ft_noise_p10_40.txt -o func_noise_p10_40.txt
Добавление шума к амплитуде и к фазе
python func2fourier.py -F 5 -P 5 -i func.txt -o ft_noise_f5p5.txt
python fourier-filter.py -r 0-40 -i ft_noise_f5p5.txt -o ft_noise_f5p5_40.txt
python fourier2func.py -i ft_noise_f5p5_40.txt -o func_noise_f5p5_40.txt
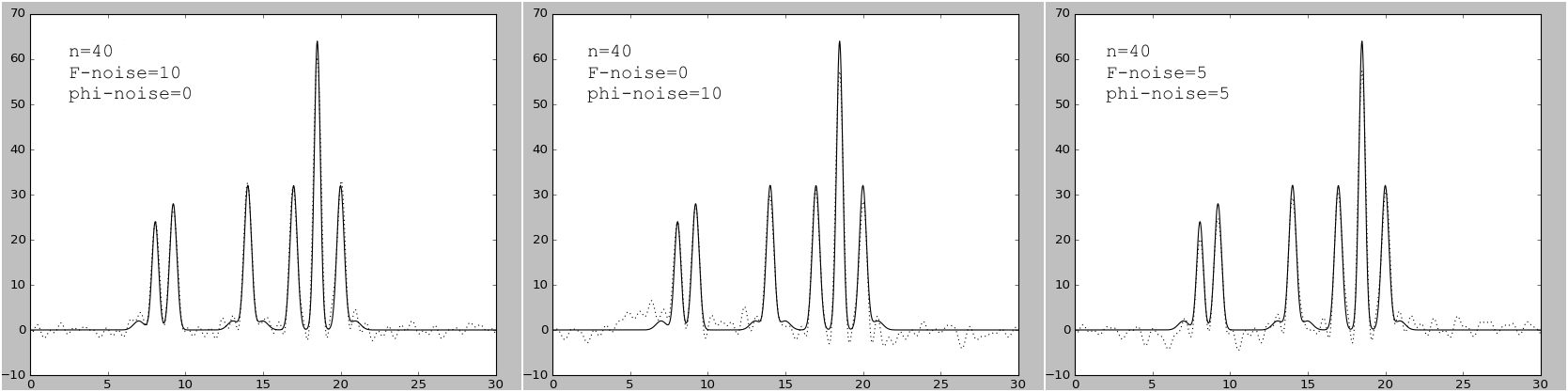 Рисунок 5.
Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 40 гармоник с шумом
10% к амплитуде; 10% к фазе; по 5% к амплитуде и фазе.
Рисунок 5.
Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 40 гармоник с шумом
10% к амплитуде; 10% к фазе; по 5% к амплитуде и фазе.
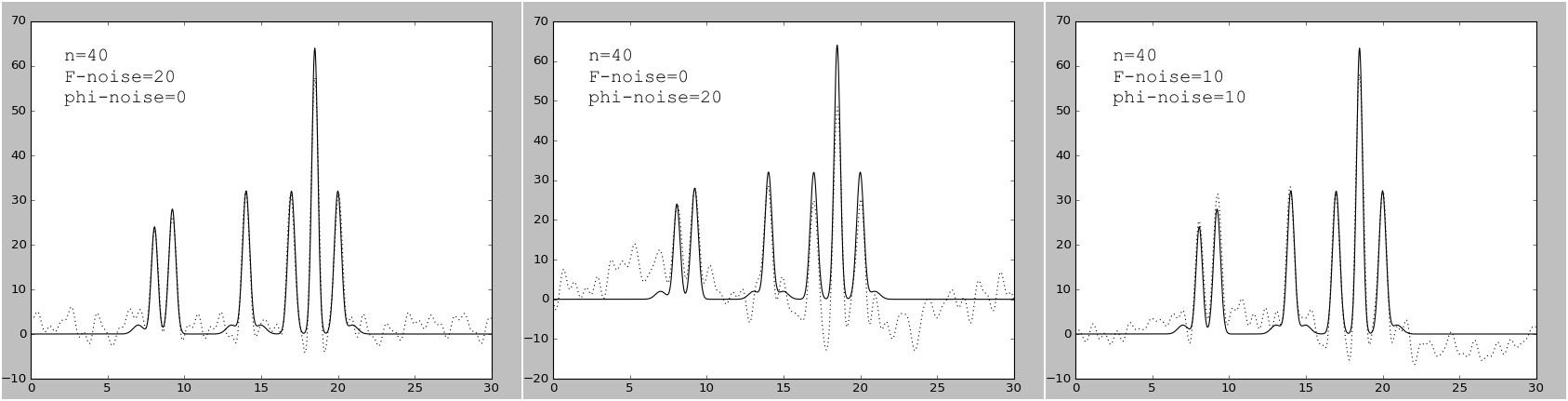 Рисунок 6.
Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 40 гармоник с шумом
20% к амплитуде; 20% к фазе; по 10% к амплитуде и фазе.
Рисунок 6.
Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 40 гармоник с шумом
20% к амплитуде; 20% к фазе; по 10% к амплитуде и фазе.
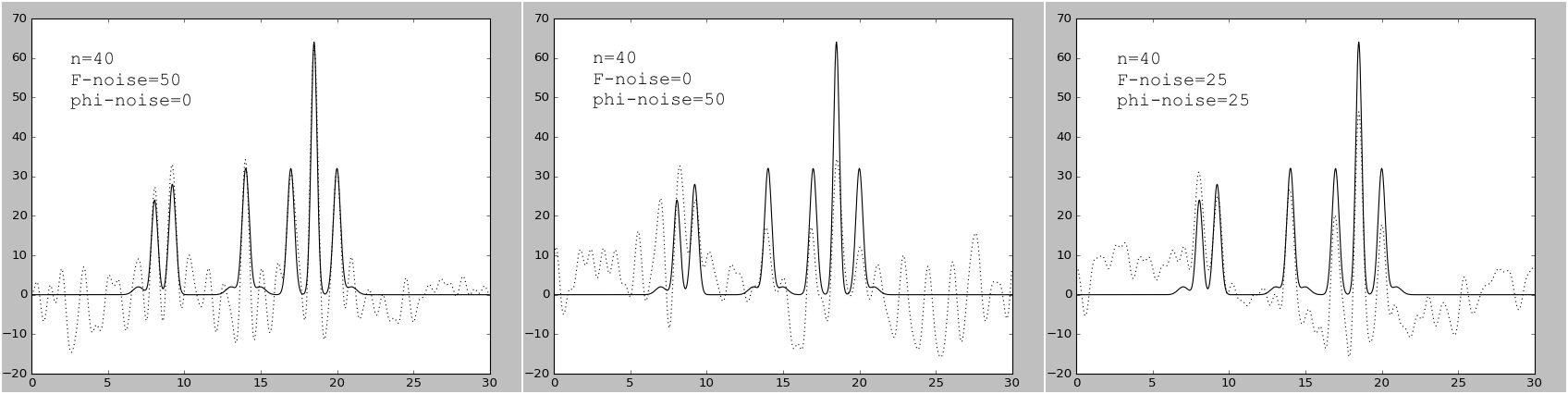 Рисунок 7.
Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 40 гармоник с шумом
50% к амплитуде; 50% к фазе; по 25% к амплитуде и фазе.
Рисунок 7.
Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 40 гармоник с шумом
50% к амплитуде; 50% к фазе; по 25% к амплитуде и фазе.
По представленным выше графикам восстановление можно оценить следующим образом:
- 10% к амплитуде; 10% к фазе; по 5% к амплитуде и фазе (рис.5) – хорошее восстановление;
- 20% к амплитуде; 20% к фазе; по 10% к амплитуде и фазе (рис.6) – среднее восстановление;
- 50% к амплитуде; 50% к фазе; по 25% к амплитуде и фазе (рис.7) – плохое восстановление.
Можно заметить, что шум в фазах вносит гораздо больший вклад в изменения, чем шум в амплитудах.
Неполные наборы гармоник
Для получения неполного набора гармоник были применены следующие команды
Удаление первой гармоники
python fourier-filter.py -r 1-40 -i func_ft.txt -o ft_begin.txt
python fourier2func.py -i ft_begin.txt -o func_begin.txt
Удаление первых двух гармоник
python fourier-filter.py -r 2-40 -i func_ft.txt -o ft_begin2.txt
python fourier2func.py -i ft_begin2.txt -o func_begin2.txt
Удаление первых трех гармоник
python fourier-filter.py -r 3-40 -i func_ft.txt -o ft_begin3.txt
python fourier2func.py -i ft_begin3.txt -o func_begin3.txt
Удаление гармоник из середины набора (19-22)
python fourier-filter.py -r 0-18,23-40 -i func_ft.txt -o ft_mid.txt
python fourier2func.py -i ft_mid.txt -o func_mid.txt
Добавление гармоники с номером n0+10
python fourier-filter.py -r 0-40,50 -i func_ft.txt -o ft_append.txt
python fourier2func.py -i ft_append.txt -o func_append.txt
Полученные изображения приведены на рисунках 8-9:
При удалении первой гармоники функция заметно смещается вниз по оси ординат, поскольку значение первой гаромоники равняется первому коэффициенту ряда Фурье - числу F0. Если же удалить первые две гармоники, то от функции вычитается синусоида с большим периодом. Если же удалить первые три, то вычитается еще синусоида, только с периодом, меньшим в два раза.
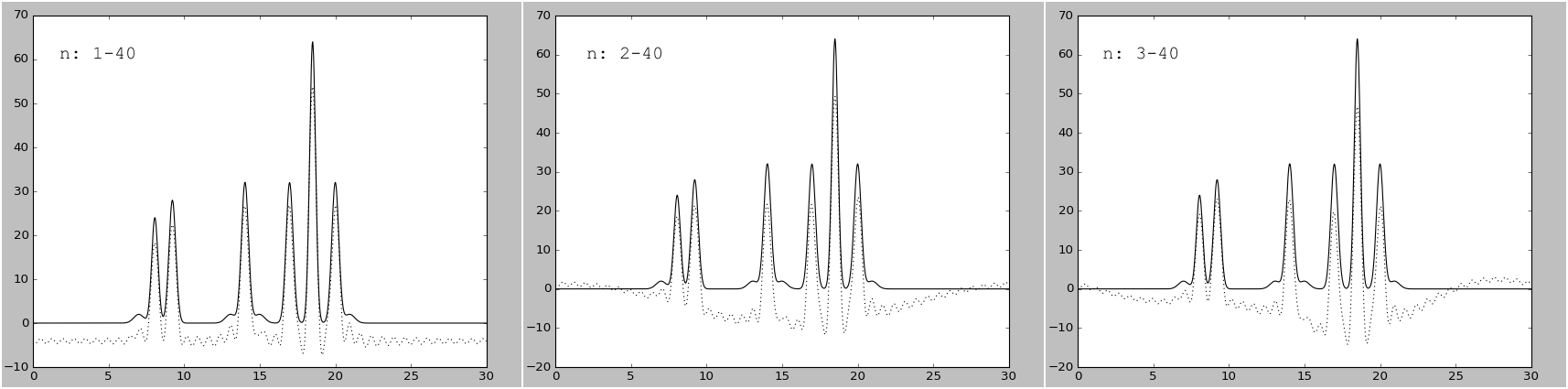 Рисунок 8. Графики восстановленных функций с неполным набором гармоник (1-40, 2-40, 3-40)
(пунктирная линия) и исходной функци (сплошная линия).
Рисунок 8. Графики восстановленных функций с неполным набором гармоник (1-40, 2-40, 3-40)
(пунктирная линия) и исходной функци (сплошная линия).
Вследствие удаления ~10% гармоник в середине набора качество восстановления сильно ухудшилось, причем настолько, что максимумы от «атомов» стали менее отличимы от шума. Добавление гармоники с номером 50 к набору гармоник 0, 1, ..., 40, к никаким заметным изменениям не привело (рисунок 9).
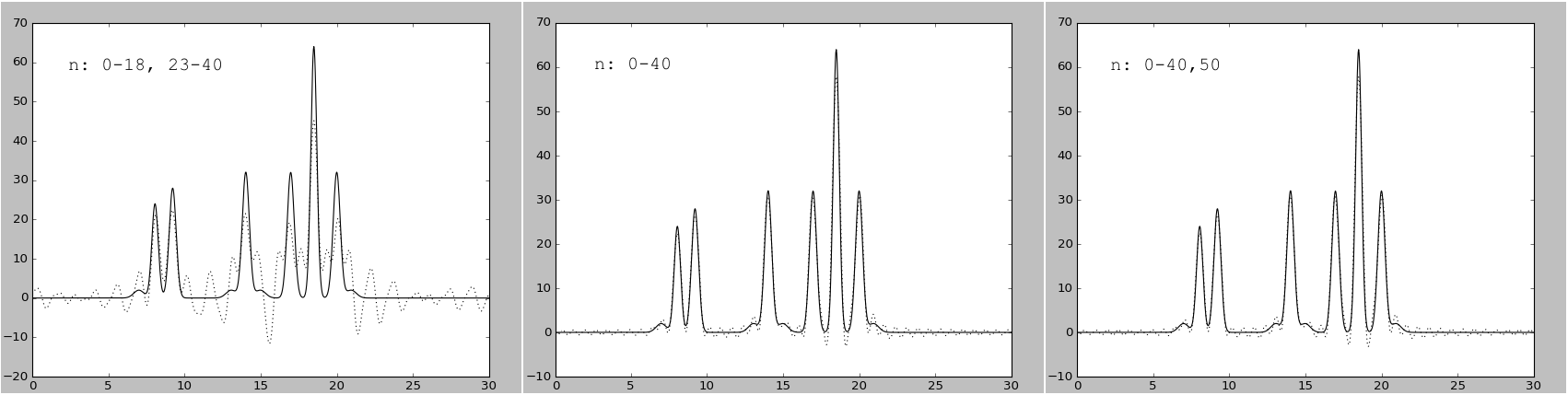 Рисунок 9. Графики восстановленных функций с неполным набором гармоник (0-18, 23-40; 0-40; 0-40,50;)
(пунктирная линия) и исходной функци (сплошная линия).
Рисунок 9. Графики восстановленных функций с неполным набором гармоник (0-18, 23-40; 0-40; 0-40,50;)
(пунктирная линия) и исходной функци (сплошная линия).
Из этого напрашивается вывод, что для восстановления функции наиболее значимыми гармониками является, те, которые находятся в середине набора. Это объясняется тем, что период гармоник, находящихся в середине набора, ближе всего к значению диаметра атомов, вследствие чего срединные гармоники имеют наибольший вклад в качество восстановления функции электронной плотности.
Определение разрешения набора гармоник
Разрешение для полного набора гармоник 0, 1, ..., 40 равно 30 Å / 41 ≈ 0,75 Å (в данном компьютерном эксперименте). Полнота данных вычисляется как процент гармоник в наборе, период которых не меньше разрешения, от числа гармоник в полном наборе для этого разрешения. Для полного набора полнота данных равна 100%.
Для неполного набора гармоник разумно всегда указывать, помимо разрешения, полноту данных. Следует понимать, что для неполного набора данных нет строгого определения разрешения и поэтому могут возникать неоднозначные ситуации. Например, если применить определение разрешения для полного набора гармоник к набору 0, ..., 40, 50, то разрешение составит ~0.6 Å, а полнота данных – 80%. Но в данной ситуации наиболее целесобразным представляется принять разрешение в ~0.75 Å. Поэтому имеет смысл вводить порог по полноте данных (напимер, в 90%), при котором "выбивающиеся" отсеиваются и делается перерасчет разрешения и полноты данных.
| Набор гармоник | Разрешение (A) | Полнота данных (%) | Шум амплитуды (% от F) | Шум фазы (% от phi) | Качество восстановления | |
|---|---|---|---|---|---|---|
| Полный набор гармоник | ||||||
| 0-498 | 0.06 | 100 | 0 | 0 | отличное | |
| 0-1 | 15 | 100 | 0 | 0 | плохое | |
| 0-10 | 2.7 | 100 | 0 | 0 | плохое | |
| 0-20 | 1.4 | 100 | 0 | 0 | среднее | |
| 0-25 | 1.2 | 100 | 0 | 0 | хорошее | |
| 0-30 | 1.0 | 100 | 0 | 0 | хорошее | |
| 0-40 | 0.73 | 100 | 0 | 0 | отличное | |
| 0-40 | 0.73 | 100 | 10 | 0 | отличное | |
| 0-40 | 0.73 | 100 | 0 | 10 | хорошее | |
| 0-40 | 0.73 | 100 | 5 | 5 | хорошее | |
| 0-40 | 0.73 | 100 | 20 | 0 | хорошее | |
| 0-40 | 0.73 | 100 | 0 | 20 | среднее | |
| 0-40 | 0.73 | 100 | 10 | 10 | среднее | |
| 0-40 | 0.73 | 100 | 50 | 0 | среднее | |
| 0-40 | 0.73 | 100 | 0 | 50 | плохое | |
| 0-40 | 0.73 | 100 | 25 | 25 | плохое | |
| Неполный набор гармоник | ||||||
| 1-40 | 0.75 | 97.5 | 0 | 0 | отличное | |
| 2-40 | 0.77 | 95 | 0 | 0 | отличное | |
| 3-40 | 0.79 | 93 | 0 | 0 | отличное | |
| 0-18, 23-40 | 0.81 | 90 | 0 | 0 | среднее | |
| 0-40, 50 | 0.73 | 100 | 0 | 0 | отличное | |