|
Статистика и линейные модели
По ссылке можно скачать или посмотреть R-скрипт с помощью которого проводились все (почти) рассчеты.
Задание 1
Выбран датасет California Housing Prices (kaggle.com).
Он содержит поля: longitude, latitude, housing_median_age, total_rooms, total_bedrooms, population, households, median_income, median_house_value, ocean_proximity. Данные можно скачать по ссылке: housing.csv.
Задание 2
В рамках задания необходимо для взятого датасета сформулировать суммарно 6 гипотез H0/H1 и проверить их правильность.
В выбранном датасете в поле ocean_proximity фигурирует 4 значения: NEAR BAY, INLAND, <1H OCEAN, NEAR OCEAN. Соответственно, я могу рассматривать данные для домов в разной удаленности от океана как отдельные выборки и сравнивать их между собой.
#1
Проверка гипотезы однородности с использованием нормального распределения.
H0: цены домов в часе езды от океана и в глубине материка распределены одинаково.
H1: цены домов распределены по-разному.
В каждой из выборок более 40 измерений, значит пользуемся знаковым тестом. Дисперсии, вообще-то не известны, но я считаю, что на таком большом объеме данных можно вычислить дисперсию с большой точностью, значит для вычисления SE я буду пользоваться выборочными дисперсиями, считая, что они очень близки к реальным дисперсиям генеральных(/ной) совокупностей(/и).
Для применения знакового теста узнаем точное количество измерений в выборках, посчитаем их среднее и дисперсию. Затем воспользуемся формулой для рассчета стандартной ошибки (при известных неравных дисперсиях) и z-значения. Формулы представлены на рис 1.
Теперь нужно пониять, насколько велика вероятность получить такое z-значение, если верна нулевая гипотеза и обе выборки принадлежат одной генеральной совокупности. Для этого рассчитаем значение функции распределения нормального распределения от квантиля равного z-значению - мы получим p-value.
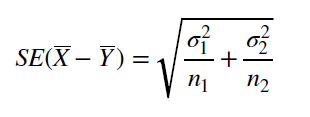
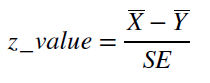
Рис 1. Формулы для рассчета SE при известных неравных дисперсиях и формула рассчета z-значения.
|
se1 = sqrt(var(h_ocean)/length(h_ocean) + var(inland)/length(inland))
z_value1 = (mean(h_ocean)-mean(inland))/se1
# z_value1 = 81.90669
pnorm(z_value1, lower.tail = F) #0
pnorm(z_value1, lower.tail = T) #1
|
z_значение оказалось равно 81.90669. То есть разница между распеределением цен домов в часе езды от океана и на метерике существенная. Вероятность получить еще большее z-значение, если верна нулевая гипотеза равна 0, значит у нас есть основание отвергнуть нулевую гипотезу об однородности распределений.
#2
Проверка гипотезы однородности с использованием распределения Стьюдента.
H0: цены домов в часе езды от океана и в глубине материка распределены одинаково.
H1: цены домов распределены по-разному.
Из каждой из выборок возьмем 12 значений (<40 измерений), пользуемся тестом Стьюдента. Дисперсии не известны, и, так как другой альтернативы для неизвестных дисперсий у нас нет, будем считать, что они равны. (Я не хочу брать дисперсии из #1, тк это бы нарушило чистоту эксперимента.) Для вычисления SE я буду пользоваться оценкой стандартного отклонения. Далее, используя средние значения для выборок и рассчитанную SE, вычислим t-значение. Формулы представлены на рис 2.
|
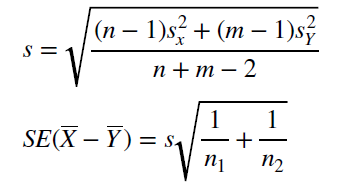
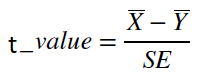
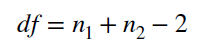
Рис 2. Формулы для рассчета SE при неизвестных равных дисперсиях, формула рассчета t-значения и df.
|
s2 = sqrt(((12-1)*sd(h_ocean_small)^2+(12-1)*sd(inland_small)^2)/(12+12-2))
se2 = s2*sqrt(1/12 + 1/12)
df2 = 12 + 12 - 2
t_value2 = (mean(h_ocean_small)-mean(inland_small))/se2
# t_value2 = 3.590202
pt(t_value2, df2, lower.tail = F) #0.0008147488
|
Теперь нужно понять, насколько велика вероятность получить такое t-значение, если верна нулевая гипотеза и обе выборки принадлежат одной генеральной совокупности. Для этого рассчитаем значение функции распределения распределения Стьюдента (с количеством степеней свобод, рассчитанным по соответствующей формуле) от квантиля равного t-значению - мы получим p-value.
t-значени оказалось равно 3.590202. То есть разница между распеределением цен домов в часе езды от океана и на метерике даже при такой маленькой выборке довольно существенная. Вероятность получить еще большее t-значение, если верна нулевая гипотеза равна 0.0008147488, значит у нас есть основание отвергнуть нулевую гипотезу об однородности распределений.
#3
Проверка гипотезы независимости с использованием распределения Хи-квадрат.
H0: соотношение дорогих и дешевых домов не зависит от того, насколько далеко эти дома расположены от океана.
H1: в разной удаленности от океана преобладает дешевое или дороге жилье.
Медиана стоимости жилья по всей Калифорнии 200000$. Подсчитаем, сколько домов стоит дешевле и дороже 200000$ в разной удаленности от океана, следовательно получим 8 групп, которые запишем в табличку (см таблицу 1).
Таблица 1. Наблюдаемое количество дорогого и дешевого
жилья в разной удаленности от океана.
| Priсe_less_200000 | Price_more_200000 |
| INLAND | 5829 | 714 |
| <1H OCEAN | 4055 | 5056 |
| NEAR BAY | 903 | 1383 |
| NEAR OCEAN | 1098 | 1551 |
|
|
median(data$median_house_value) #~200000
str1 = c(group0, group2, group4, group6)
str2 = c(group1, group3, group5, group7)
table1 <- data.frame('Priсe_less_200000' = str1,
'Price_more_200000' = str2)
|
Проверим независимость параметров с помощью встроенного теста Хи-квадрат.
chisq.test(table1) # X-squared = 3888.2, df = 3, p-value < 2.2e-16
#df = (4-1)*(2-1) = 3
Получить такие данные если верна гипотеза о независимости очень маловероятно (p-value < 2.2e-16), значит у нас есть основания отвергнуть Н0.
Теперь проверим тоже самое, но посчитаем значение Хи-квадрата вручную. По алгоритму, изложенному в презентации (см таблицу 1.1), можно рассчитать таблицу ожидаемых значений (см таблицу 2), затем применить формулу, показанную на рис.3 и проанализировать результат.
Таблица 1.1. Данные для рассчета ожидаемых значений.
| Priсe_less_200000 | Price_more_200000 | Сумма | Вероятность |
| INLAND | 5829 | 714 | 6543 | 0.32 |
| <1H OCEAN | 4055 | 5056 | 9111 | 0.44 |
| NEAR BAY | 903 | 1383 | 2286 | 0.11 |
| NEAR OCEAN | 1098 | 1551 | 2649 | 0.13 |
| Сумма | 11885 | 8704 | 20589 | |
| Вероятность | 0.58 | 0.42 | | |
Таблица 2. Ожидаемое количество дорогого и дешевого
жилья в разной удаленности от океана.
| Priсe_less_200000 | Price_more_200000 |
| INLAND | 3821 | 2767 |
| <1H OCEAN | 5254 | 3805 |
| NEAR BAY | 1314 | 951 |
| NEAR OCEAN | 1553 | 1124 |
|
str1_exp = c(3821, 5254, 1314, 1553)
str2_exp = c(2767, 3805, 951, 1124)
table1_exp <- data.frame('Priсe_less_200000' = str1_exp,
'Price_more_200000' = str2_exp)
|
| |
|
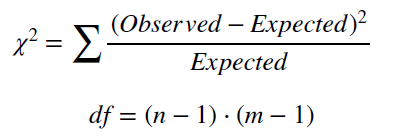
Рис 3. Формула для рассчета значения Хи-квадрат и df.
|
chisq3 = ((table1[1,1]-table1_exp[1,1])^2)/table1_exp[1,1] + ...
+ ((table1[4,2]-table1_exp[4,2])^2)/table1_exp[4,2]
# chisq3 = 3883.716
# df = (4-1)*(2-1) = 3
|
Значение хи-квадрат с df=3 на уровне значимости 0.01 равно 11.341, значит на основании полученного chisq3 = 3883.716 мы отвергаем гипотезу о независимости.
#4
Проверка на Goodness of fit с использованием распределения Хи-квадрат.
H0: количество продаваемых домов распределено равномерно по регионам в разной удаленности от океана.
H1: модель равномерного распределения плохо описывает имеющиеся данные.
Для проверки гипотезы посчитаем среднее количество подаваемого жилья, запишем это число в столбец ожидаемых значений (см таблицу 3) и с помощью теста хи-квадрат проверим, насколько хорошо такая можель соответствует реальному распределению количеству продаваемых домов в разных регионах (эти выборки обозначены как group**) (см рис. 4).
Таблица 3. Наблюдаемые и ожидаемые значения
количества продаваемых домов.
| Real | Expected |
| INLAND | 6551 | 6551 |
| <1H OCEAN | 9136 | 6551 |
| NEAR BAY | 2290 | 6551 |
| NEAR OCEAN | 2658 | 6551 |
|
mean(group00, group11, group22, group33) # 6551
str11 = c(group00, group11, group22, group33)
str22 = c(6551, 6551, 6551, 6551)
table2 <- data.frame('Real' = str11, 'Expected' = str22)
|
| |
|
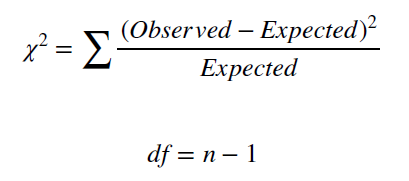
Рис 4. Формула для рассчета значения Хи-квадрат и df.
|
chisq.test(table2) # X-squared = 3512.8, df = 3, p-value < 2.2e-16
# df = 4 - 1 = 3
chisq4 = ((group00-6551)^2)/6551 + ((group11-6551)^2)/6551 +
((group22-6551)^2)/6551 + ((group33-6551)^2)/6551
# chisq4 = 6104.991
|
Почему-то при подсчете значения хи-квадрат с помощью встроенного теста и вручную получились разные значения... Однако p-value < 2.2e-16 свидетельствует о том, что Н0 нужно отклонить (а в случае ручного подсчета получается еще большее значение хи-квадрат, так что сомнений, что можель равномерного распределения плохо описывает данные нет).
#5
Построим двусторонний доверительный интервал для среднего значения возраста продаваемого в Калифорнии жилья. Будем пользоваться нормальным распределением, так как у нас более 40 измерений. Формулы представлены на рис. 5.
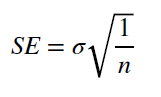
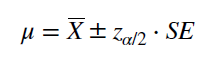
Рис 5. Формулы для рассчета доверительного интервала.
|
mean(house_age) #28.63949
se5 = sd(house_age)/sqrt(length(house_age))
left = mean(house_age) + se5*qnorm((1-0.95)/2) # left = 28.46779
right = mean(house_age) + se5*qnorm((1+0.95)/2) # right = 28.81118
|
Таким образом, оцениваемое среднее с вероятностью 0.95 лежит в интервале [28.46779; 28.81118].
#6
Построим одноронний доверительный интервал для среднего значения возраста продаваемого в Калифорнии жилья. Будем пользоваться нормальным распределением, так как у нас более 40 измерений. Формулы представлены на рис. 6.
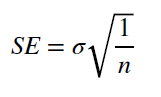
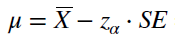
Рис 5. Формулы для рассчета правостороннего доверительного интервала.
|
mean(house_age) #28.63949
se5 = sd(house_age)/sqrt(length(house_age))
left6 = mean(house_age) + se5*qnorm(1-0.95) # left6 = 28.49539
|
Таким образом, оцениваемое среднее с вероятностью 0.95 лежит в интервале [28.49539; ∞].
Задание 3
Проверим, нормально ли распределены цены домов около океана. Для этого построим гистограмму (рис. 7) и QQ-plot (рис. 8) для данного распределения.
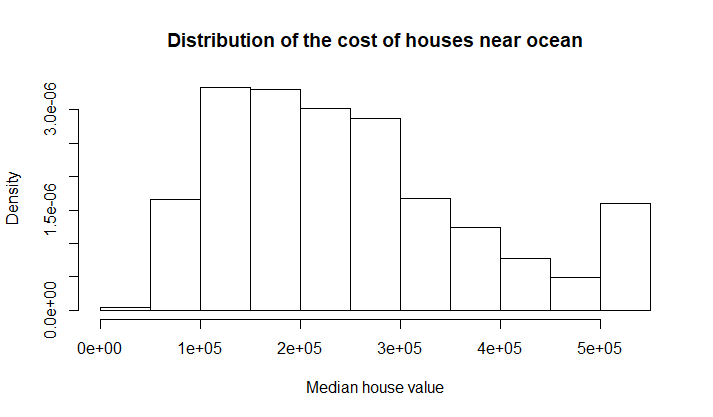
Рис 7. Гистограмма распределения цен домов около океана.
|
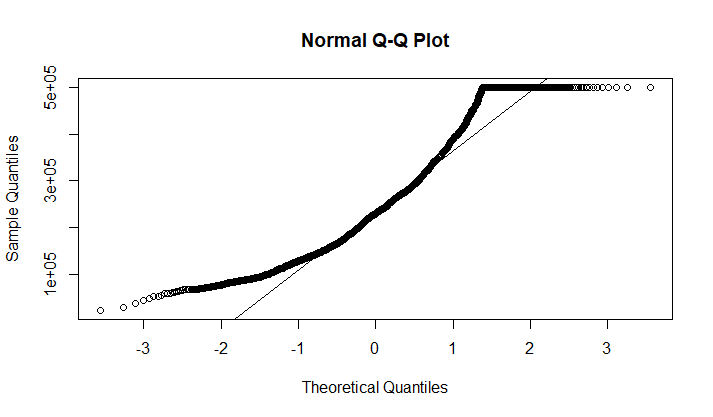
Рис 8. QQ-plot.
|
По гистограмме (рис 9) и QQ-plot (рис 8) видно, что данное распределение рядом особенностей отличается от нормального. Во-первых, по форме QQ-plot (отклонение краевых точек в верхнюю полуплоскость) можно сказать, что у нас имеется ассимметрия в виде сдвига влево. Во-вторых небольшой сигмоидный участок в правом верхнем углу QQ-plot свидетельствует о том, что слева у нас присутствует "тяжелый хвост". Данные наблюдения подтверждаются при анализе гистограммы - сдвиг влево и очень тяжелый правый хвост.
О чем говорит такое наблюдение с человеческой точки зрения? О том, что около океана преобладает более дешевое жилье, но есть также некое количество очень дорогих домов. Логично - по совсем низким ценам жилье не продают застройщики, население в основном предпочитает жилье подешевле, но есть также элитные дома.
Также для проверки распределения на нормальность требуется применить специальные тесты. Применим (строгий) тест Шапиро-Уилка - получаем p-value < 2.2e-16, значит гипотеза нормальности отвергается. Проверим тоже самое с помощью теста Колмогорова-Смирнова. Если провести One-sample тест, то есть просто сравнить с нормальным распределением, получаем p-value < 2.2e-16. Если провести Two-sample тест, для которого сгенерировать нормальное распределение с ровно таким же количеством измерений, тем же средним и стандартным отклонением, как в нашей выборке, получаем p-value = 1.225e-06. То есть и в том и в другом случае гипотезу о нормальности распределения отвергаем. Можно было бы еще проверить с помощью критерия согласия Хи-квадрат, но мне лень.
shapiro.test(near_ocean) # p-value < 2.2e-16
ks.test(near_ocean, "pnorm") # p-value < 2.2e-16
ks.test(near_ocean, rnorm(length(near_ocean), mean(near_ocean), sd(near_ocean))) # p-value = 1.225e-06
Задание 4
Проведем проверку на выбросы в нашем распределении. Воспользуемся для этого графическим изображением данных в виде boxplot (рис. 9) и диаграммы Кливленда, постоенной для отсортированного массива данных (рис. 10).
boxplot(near_bay)
dotchart(sort(near_bay))
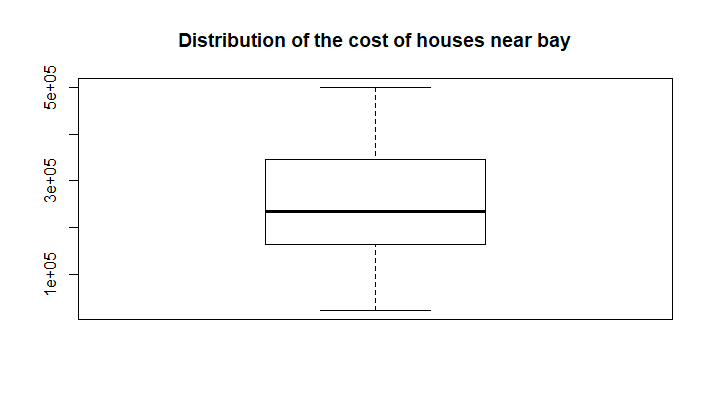
Рис 9. Boxplot распределения цен домов около залива.
|
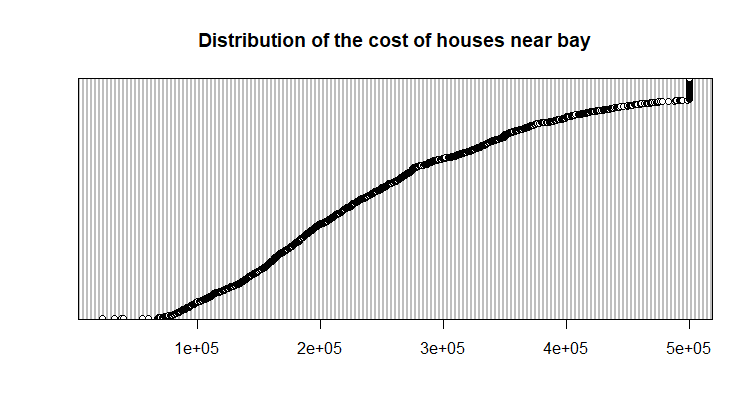
Рис 10. Диаграммы Кливленда распределения цен домов около залива.
|
На диаграмме Кливленда видно, что есть выбросы в правой части распределения - то есть неожиданно большое количество дорогих домов. На графике Boxplot выбросы не показаны, значит данные выборки "укладываются в распределение" (в расстояние между усами - я не знаю, как сказать). Чтобы проверить, как выглядит распределение, можно построить гистограмму и QQ-plot для этого распределения (рис. 11 и 12).
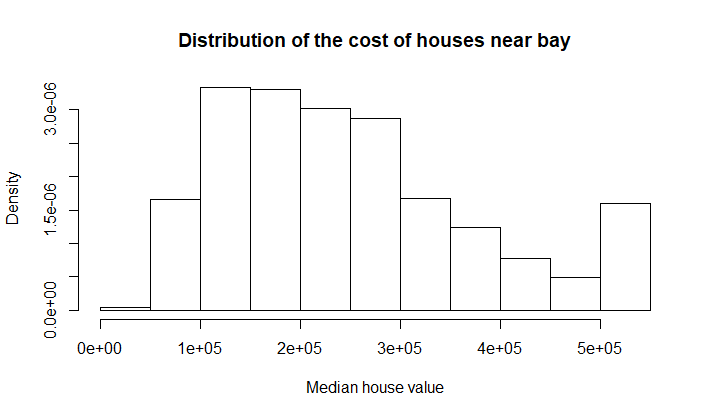
Рис 11. Гистограмма распределения цен домов около залива.
|
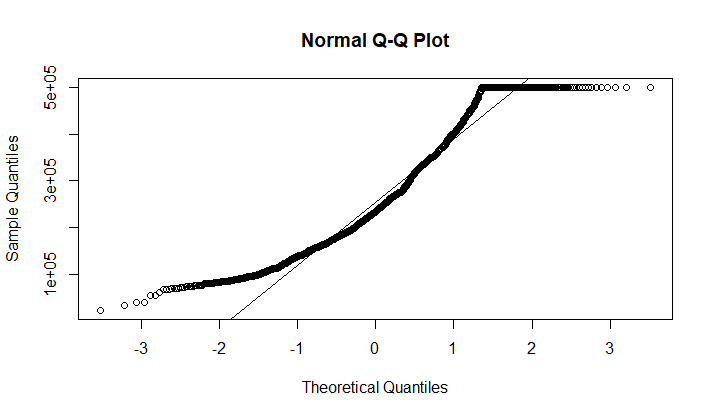
Рис 12. QQ-plot.
|
Ситуация с распределением тут ровно такая же как и среди домов около океана (см задание 3). Явных выбросов не наблюдается.
Задание 5
Множественное тестирование.
Поправки:
- FWER (Family-Wise Error Rate) - вероятность того, что среди тестов будет получен хотя бы один ложноположительный результат, меньше заданного порога α
- FDR (False Discovery Rate) - процент ложноположительных результатов не больше некого заданного порога α
Сгенерируем 1000 рандомных парных стандартных нормальных выборок по 100 значений в каждой. Для каждой пары выборок проверим гипотезу об однородности с помощью t-теста и запишем в массив 1000 полученных p-value.
|
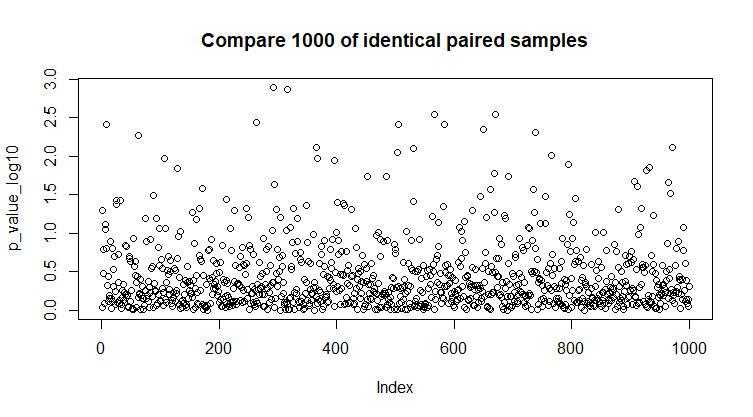 <.p> <.p>
Рис 13. Сравнение 1000 рандомных парных стандартных нормальных выборок.<.p>
|
p_value = NULL
for(i in 1:1000){
before = rnorm(100)
after = rnorm(100)
p_value[i] = t.test(before, after)$p.value
}
|
Применим поправки:
- FWER. Применим Holm-Bonferonni: α = 0.01
- FDR. Применим Benjamini & Hochberg: α = 0.1
|
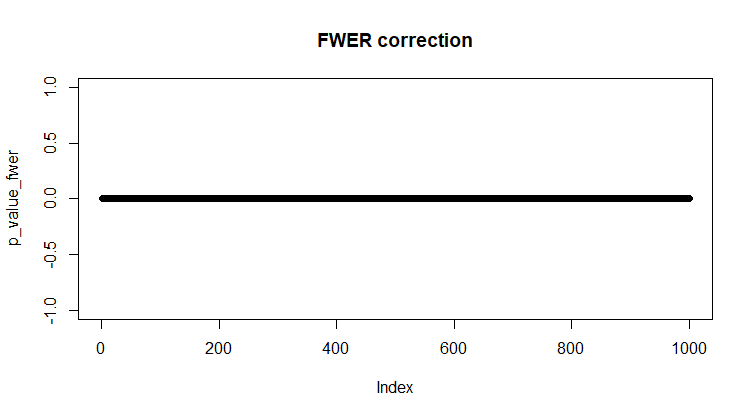
Рис 14. Сравнение 1000 одинаковых выборок с поправкой Холма-Бонферрони, α = 0.01.
|
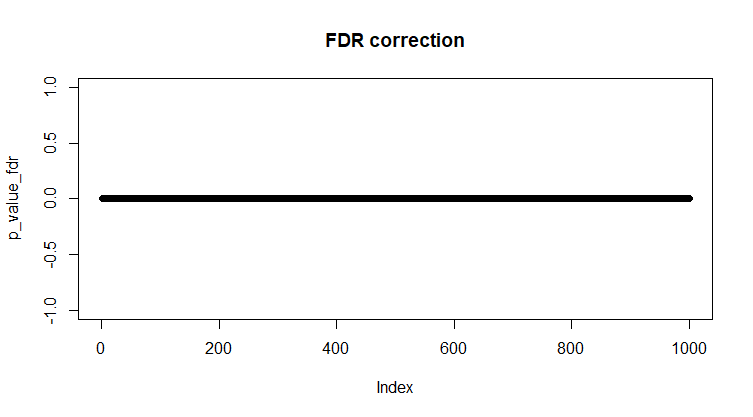
Рис 15. Сравнение 1000 одинаковых выборок с поправкой Бенжамина и Хокберга, α = 0.01.
|
| |
correction_fwer = p.adjust(p_value, method = "holm") < 0.01
any(correction_fwer) #FALSE
p_value_fwer = p_value*correction_fwer
plot(p_value_fwer)
|
correction_fdr = p.adjust(p_value, method = "BH") < 0.1
any(correction_fdr) #TRUE
p_value_fdr = p_value*correction_fdr
plot(p_value_fdr)
|
Сгенерируем 990 рандомных парных стандартных нормальных выборок по 100 значений в каждой и 10 рандомных нормальных выборок с mean = 3 & sd = 5. Для каждой пары выборок проверим гипотезу об однородности с помощью t-теста и запишем в массив 1000 полученных p-value.
|
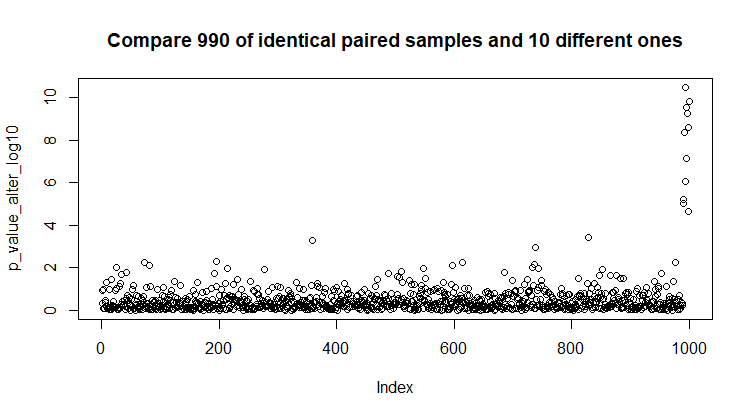
Рис 16. Сравнение 990 рандомных парных стандартных нормальных выборок и 10 отличающихся.
|
p_value_alter = NULL
for(i in 1:990){
before = rnorm(100)
after = rnorm(100)
p_value_alter[i] = t.test(before, after)$p.value
}
for(i in 990:1000){
before = rnorm(100)
after = rnorm(100, 3, 5)
p_value_alter[i] = t.test(before, after)$p.value
}
|
Применим поправки:
- FWER. Применим Holm-Bonferonni: α = 0.01
- FDR. Применим Benjamini & Hochberg: α = 0.1
|
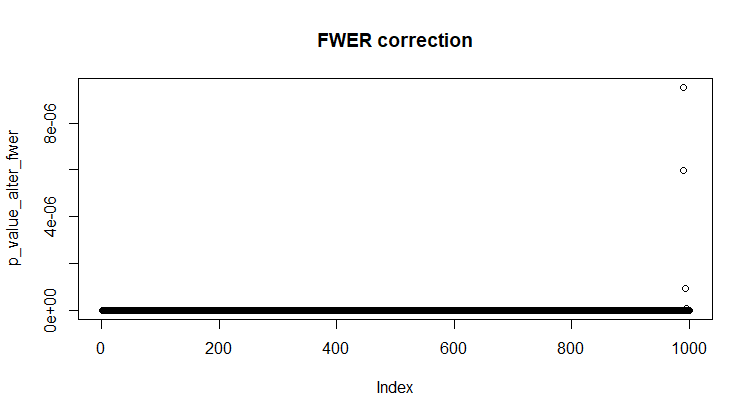
Рис 17. Сравнение 990 одинаковых выборок и 10 отличающихся с поправкой Холма-Бонферрони, α = 0.01.
|
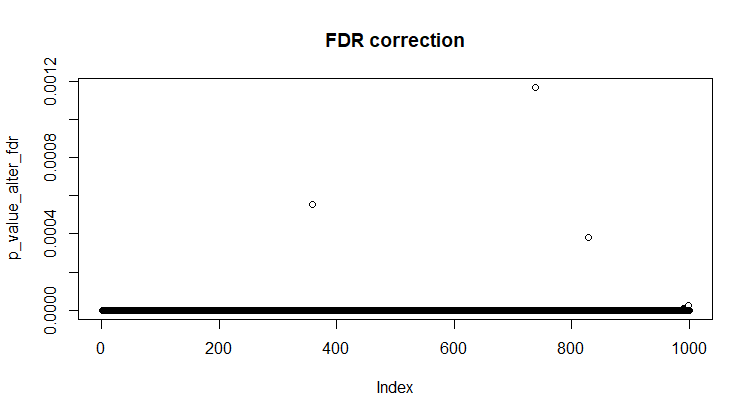
Рис 18. Сравнение 990 одинаковых и 10 отличающихся выборок с поправкой Бенжамина и Хокберга, α = 0.01.
|
| |
correction_alter_fwer = p.adjust(p_value_alter, method = "holm") < 0.01
any(correction_alter_fwer) #TRUE
p_value_alter_fwer = p_value_alter*correction_alter_fwer
plot(p_value_alter_fwer, main="FWER correction")
|
correction_alter_fdr = p.adjust(p_value_alter, method = "BH") < 0.1
any(correction_alter_fdr) #TRUE
p_value_alter_fdr = p_value_alter*correction_alter_fdr
plot(p_value_alter_fdr)
|
Вывод из этого всего - поправка на множественное сравнение обеспечивает надежную защиту от ложноположительных результатов. Однако, судя по графикам 17 и 18, эти поправки достаточно суровы, чтобы из 10, действительно отличающихся парных выборок, пропустить как значимо различающиеся только 3.
Задание 6
Построение линейной регрессии, которая будет предсказывать цены домов, основываясь на некоторых факторах. Я буду рассматривать в качестве факторов, влияющих на цены домов следующие: возраст дома, общее количество камнат, количество спален и средний доход неселения в регионе. Думаю, все эти параметры можно считать независимыми.
Линейная регрессия имеет вид Y = X*β + ε, где Y - вектор откликов (предсказываемая величина), X - матрица факторов регрессии (значения параметров, от которых зависят цены домов), β - вектор коэффициентов регрессии (именно их мы получаем при рассчете модели) и ε - вектор ошибок (обычно про них есть ряд предположений, позволяющих с ними работать).
Для обучения будем использовать данные для домов, которые продаются около залива. И, в качестве эксперимента, попробуем использовать для обучения только те из них, которые стоят меньше 200000$.
Для того, чтобы система работала, требуется заменить пустые ячейки средним значением по столбцу или выкинуть целиком строку с пропущенными значениями. Я выбираю первый вариант.
learning_set <- data[data$ocean_proximity == 'NEAR BAY',]
model = lm(median_house_value ~ housing_median_age + total_rooms + total_bedrooms + median_income, data=learning_set)
summary(model)
learning_set2 <- data[data$ocean_proximity == 'NEAR BAY' & data$median_house_value < 200000,]
model2 = lm(median_house_value ~ housing_median_age + total_rooms + total_bedrooms + median_income, data=learning_set2)
summary(model2)
Функция summary выдает данные построенной модели (см. таблицы 4, 5). Теперь мы знаем коэффициенты с которыми входят факторы регрессии в выражение, и знаем, насколько это достоверно, то есть насколько реально удалось выявить зависимость значений предсказываемой переменной от факторов. Для первой модели эти показатели очень хорошие, зависимость достоверна (p-value очень маленькие). Для воторой модели (которая построена на основе данных только по дешевым домам) показатели сильно хуже, в частности, получилось, что цена дома не зависит от возраста этого дома и почти не зависит от количества комнат.
Таблица 4. Модель, обученная на данных о домах около залива.
Coefficients:
(Intercept) housing_median_age total_rooms total_bedrooms median_income
-66919.92 2550.94 -27.58 189.34 48189.13
Estimate Std. Error t value Pr(>|t|)
(Intercept) -66919.919 8774.841 -7.626 3.53e-14 ***
housing_median_age 2550.945 148.713 17.153 < 2e-16 ***
total_rooms -27.583 2.859 -9.648 < 2e-16 ***
total_bedrooms 189.340 13.751 13.769 < 2e-16 ***
median_income 48189.129 1098.309 43.876 < 2e-16 ***
Таблица 5. Модель, обученная на данных о домах около залива, дешевле 200000.
Coefficients:
(Intercept) housing_median_age total_rooms total_bedrooms median_income
84313.292 -84.365 -5.398 32.787 19444.257
Estimate Std. Error t value Pr(>|t|)
(Intercept) 84313.292 6123.663 13.768 < 2e-16 ***
housing_median_age -84.365 96.410 -0.875 0.38177
total_rooms -5.398 2.344 -2.303 0.02150 *
total_bedrooms 32.787 10.024 3.271 0.00111 **
median_income 19444.257 1155.214 16.832 < 2e-16 ***
Теперь в качестве тестовых данных возьмем всю остальную информацию о домах в Калифорнии и проверим на них качество работы наших моделей. Для тестового датасета тоже требуется заполнить или удалить пустые ячейки.
test_set <- data[data$ocean_proximity != 'NEAR BAY',]
predictResult <- predict(model, test_set)
predictResult2 <- predict(model2, test_set)
Проверять качество обучения будем с помощью Min Max accuracy и MAPE. Эти показатели качества обучения по сути показывают, насколько предсказанные значения отклоняются от реальных. Формулы см на рис. 19.

Рис 19. Min Max accuracy и MAPE.
Для того, чтобы применить вышеозначенные критерии качества обучения, требуется датафрейм, содержащий предсказанные и реальные значения цен домов. Можно оценить насколько эти значения соответствуют друг другу, рассчитав коэффициент корреляции между двумя столбцами. В случае первой модели предсказанные значения совпадают с реальными на 73%, а в случае "ущербной" модели на 71% (то есть вообще-то она может тоже нормально работает).
actuals_preds <- data.frame(cbind(actuals=test_set$median_house_value, predicteds=predictResult))
correlation_accuracy <- cor(actuals_preds)
actuals predicteds
actuals 1.000000 0.726244
predicteds 0.726244 1.000000
actuals_preds2 <- data.frame(cbind(actuals=test_set$median_house_value, predicteds=predictResult2))
correlation_accuracy2 <- cor(actuals_preds2)
actuals predicteds
actuals 1.0000000 0.7073301
predicteds 0.7073301 1.0000000
Критерии рассчитываются по формулам (рис. 19).
# min_max accuracy and mean absolute percentage error
min_max_accuracy <- mean(apply(actuals_preds, 1, min) / apply(actuals_preds, 1, max)) # 0.7339644
mape <- mean(abs((actuals_preds$predicteds - actuals_preds$actuals))/actuals_preds$actuals) # 0.4293735
min_max_accuracy2 <- mean(apply(actuals_preds2, 1, min) / apply(actuals_preds2, 1, max)) # 0.7119408
mape2 <- mean(abs((actuals_preds2$predicteds - actuals_preds2$actuals))/actuals_preds2$actuals) # 0.3701025
Насколько я понимаю, значение min_max_accuracy (MMA) для идеальной линейной регрессии стремится к 1, а MAPE стремится к 0. У нас получилось, что для первой модели MMA = 73%, MAPE = 43%; а для второй MMA = 71%, MAPE = 37%.
По значениям MMA обе модели почти равноправны, первая немного лучше. По значениям MAPE получается, что вторая модель работает лучше, что немного странно, тк она обучалась на неполных данных. Не знаю, почему так получилось. Но в целом обе модели работают нормально, значит обучение было успешным.
© Darya Potanina, 2017
|
|
|
|
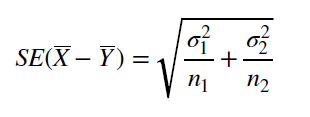
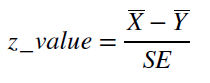
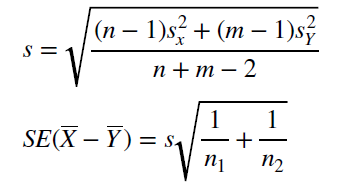
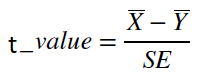
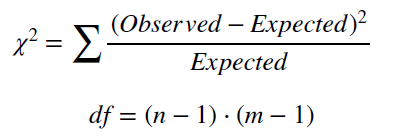
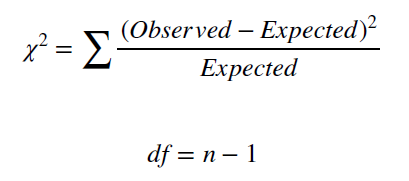
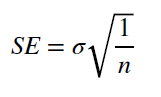
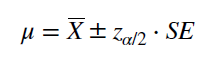






 <.p>
<.p>





