Рентгеноструктурный анализ

Исследование качества восстановления функции ЭП от одной переменной в зависимости от того, какие и сколько гармоник ряда Фурье используются для ее восстановления

Текст задания: практикум 3. Все требующиеся для выполнения задания скрипты были переписаны с python2 на python3.

Сокращения

ЭП - электронная плотность

Создание функции ЭП

Для компьютерного эксперимента была взята модель со следующими характеристиками:

На отрезке [0,30] (Å) расположены две молекулы.
Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 Å друг от друга.
Молекулы расположены на расстоянии 3-5 Å (водородная связь или гидрофобное взаимодействие между ними).
Всего в системе 5-7 атомов.

Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме. Гауссова функция определяется числами λ, β, γ по формуле: gauss = λ*exp(-(β^2)*(X-γ)^2). Я использовала эти значения из variant3.txt. Таким образом задается распределение электронной плотности для каждого атома - высота пика, ширина пика, координата максимума пика соответсвенно. Рассчитывается функция ЭП с помощью скрипта compile-func_py3.py.

python compile-func_py3.py -g 41,3.2,24.5+21,3.7,27.5+31.0,3.2,30+10,2,10

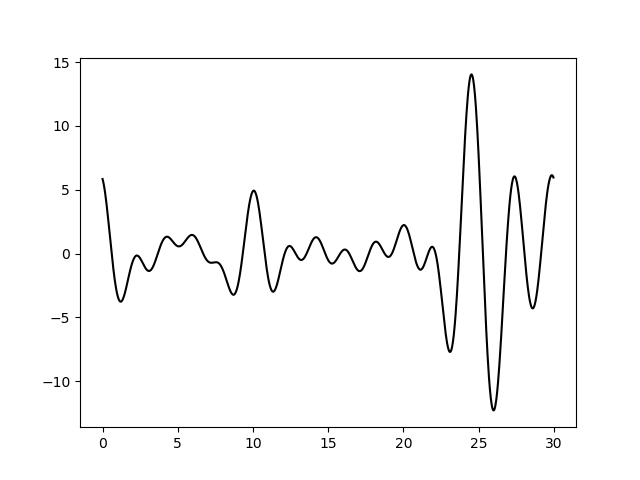
Указанный скрипт выдал текстовый файл func.txt и изображение функции электронной плотности (см рис 1). В данном случае система состоит из 1 + 2 атомов.

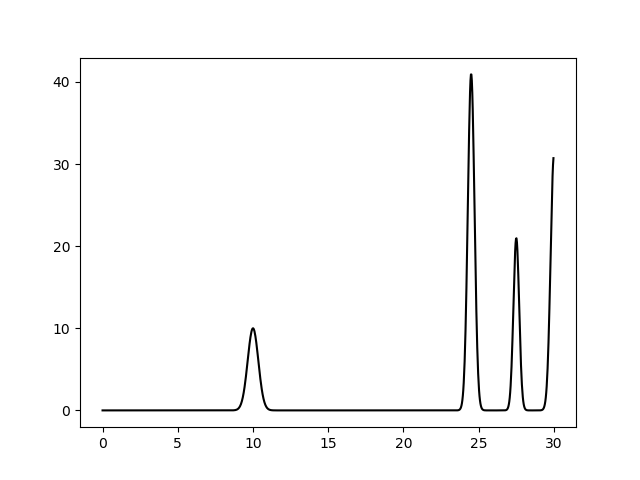
Рисунок 1. Изображение функции электронной плотности, полученное в результате компьютерного эксперимента.

Расчет коэффициентов Фурье

Для функции ЭП, полученной на предыдущем этапе, были рассчитаны амплитуды и фазы сигналов (скрипт func2fourier_py3.py). Скрипт выдал файл func_ft.txt, содержащий 499 гармоник.

python func2fourier_py3.py -i func.txt

Отбор необходимого числа гармоник и восстановление исходной функции ЭП по полному набору гармоник

Из полученных 499 гармоник было отобрано необходимое для восстановления функции количество гармоник. Скрипт, выполняющий эту операцию - fourier-filter_py3.py. Параметр -r позволяет "вырезать" гармоники с указанными номерами.

python fourier-filter_py3.py func_ft.txt -r 0-15

Для того, чтобы увидеть результат "фильтрации" используется скрипт fourier2func_py3.py, входным файлом для которого является func_ft_filtered.txt, который выдает "фильтрующий скрипт (этотот файл делается новый в каждом эксперименте, соответственно, ссылка на версию последней итерации).

python fourier2func_py3.py func_ft_filtered.txt

Так как нам известно разрешение всех гармоник в наборе, этот набор гармоник полный. Если включать в этот набор разное количество гармоник от 0-й до n-й, картинка восстановления ЭП будет немного разной. Качество восстановления характеризуется так:

Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов").
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума.
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно.
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".

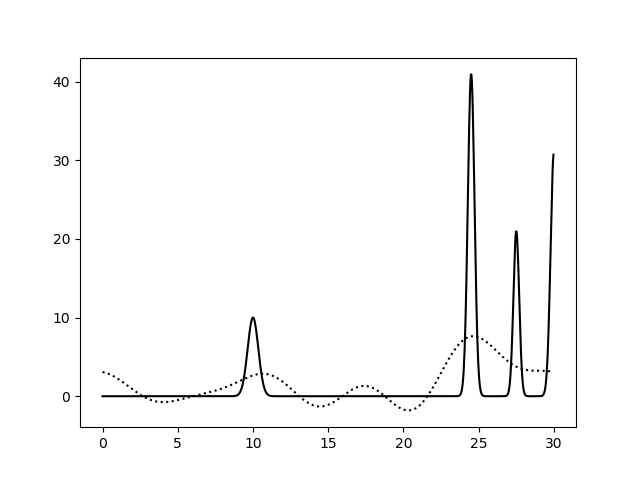
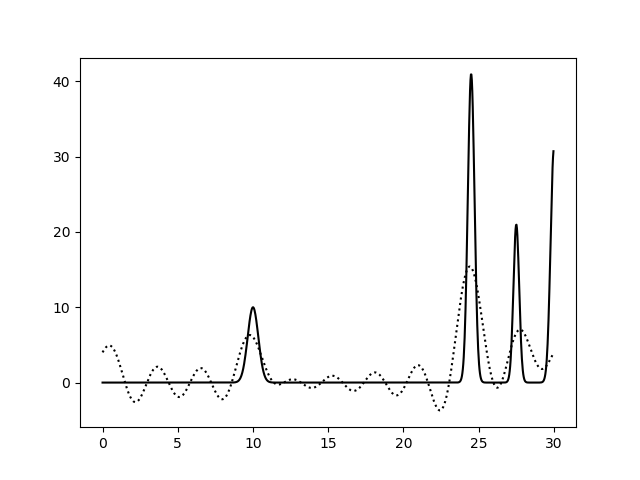
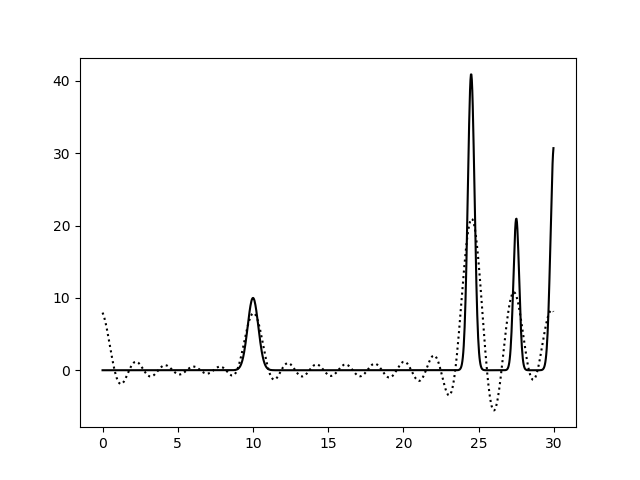
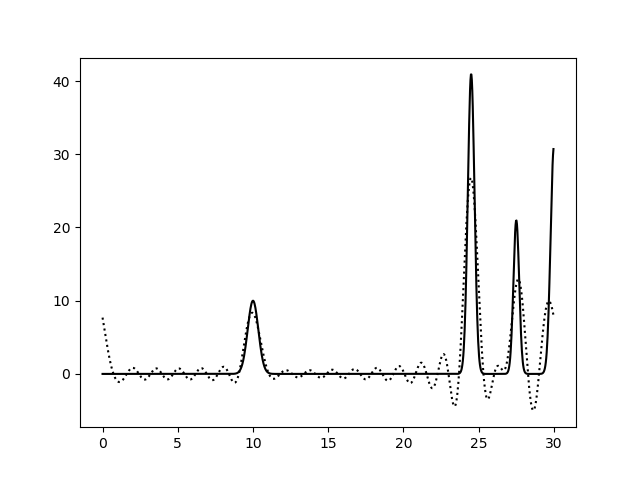
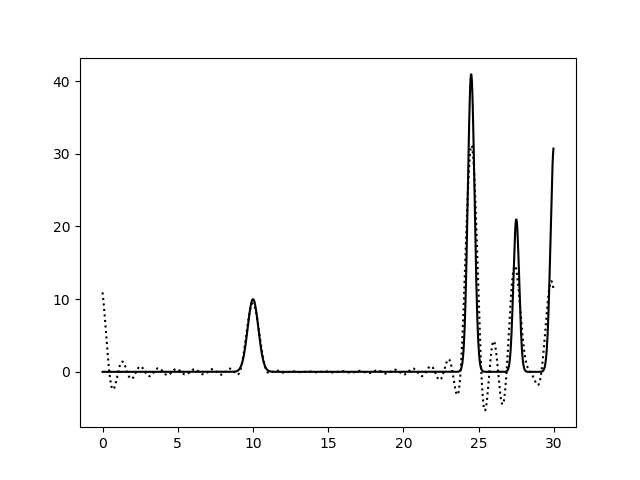
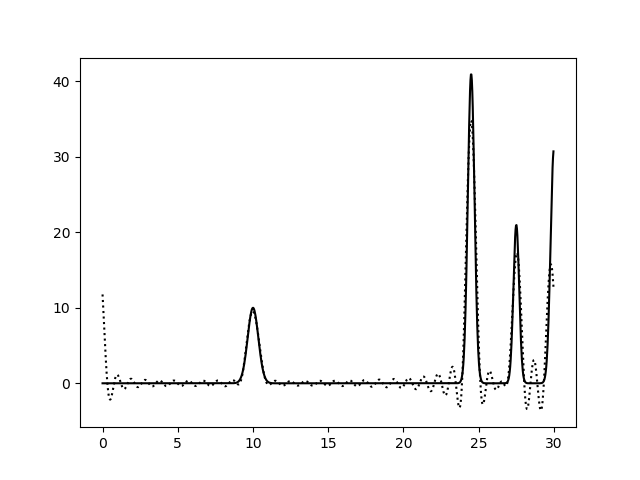
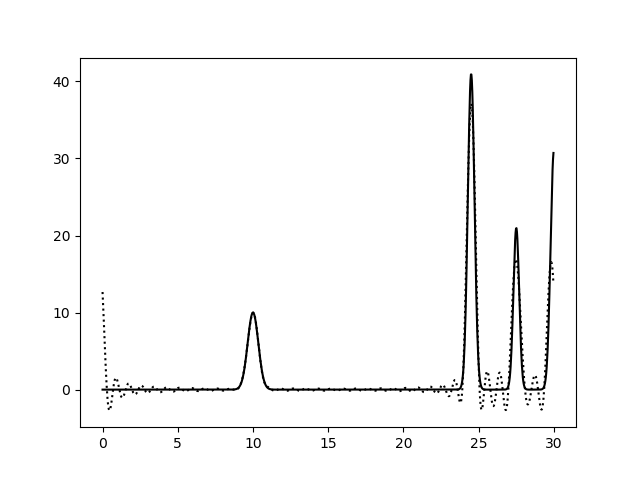
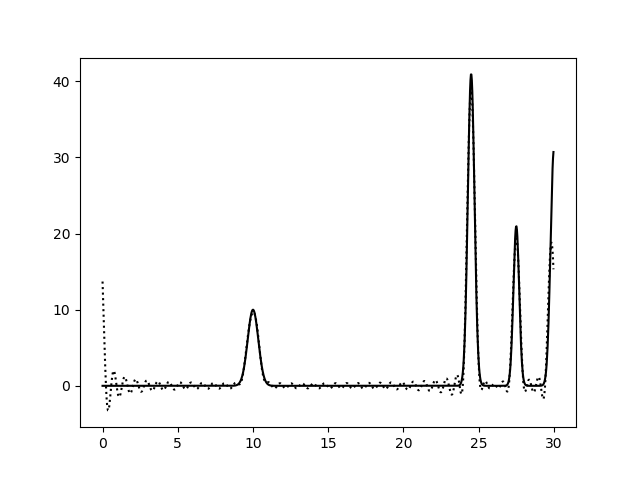
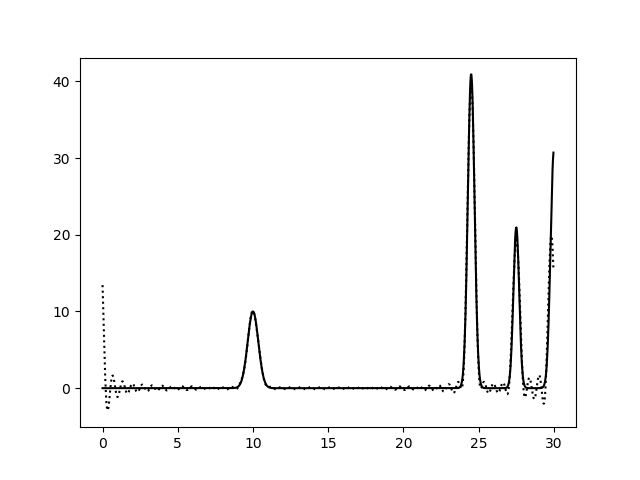
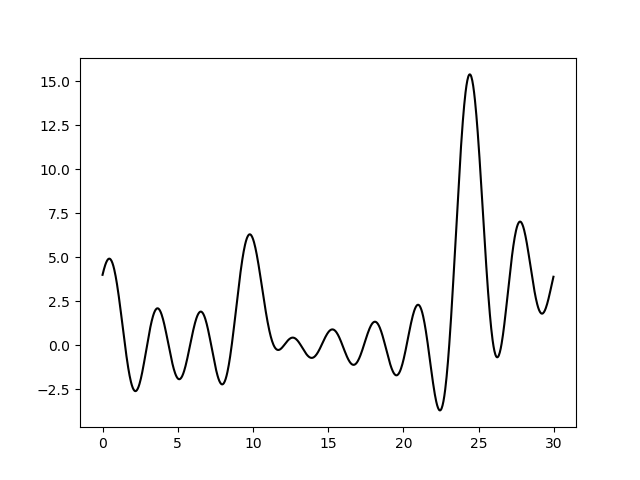
На рисунках 2-10 представлены графики функций ЭП, восстановленные по полным наборам гармоник разных размеров. Сплошной линией обозначен график исходной функции ЭП, пунктирной линией - восстановленной. Сигналы на самых границах интервала я не учитывала при анализе.

Пики на концах интерсвала аппроксимируются крайне плохо, добиться хорошей их аппроксимации мне не удалось, поэтому я решила забить. Вероятно, надо было взять другую функцию.

Судя по этим графикам, для отличного восстановления функции ЭП хватает полного набора гормоник от 0-й до 15-й. Набор из гармоник от 0-й до 40-й полностью повторяет функцию ЭП, в том числе точную высоту пиков. Включение в набор гармоник с более высоким разрешением уже не вносит никакой вклад в качество восстановления.

Рисунок 2. Гармоники от 0-й до 5-й. Рисунок 3. Гармоники от 0-й до 10-й. Рисунок 4. Гармоники от 0-й до 15-й.

Рисунок 5. Гармоники от 0-й до 20-й. Рисунок 6. Гармоники от 0-й до 25-й. Рисунок 7. Гармоники от 0-й до 30-й.

Рисунок 8. Гармоники от 0-й до 35-й. Рисунок 9. Гармоники от 0-й до 40-й. Рисунок 10. Гармоники от 0-й до 45-й.

Восстановление исходной функции ЭП при добавлении гауссового шума к амплитудам и фазам

Чтобы сделать модель более приближенной к реальности, к амплитудам и фазам на стадии определения набора гармоник был добавлен гауссовский шум. Делается это с помощью параметров -F для амплитуд и -P для фаз. Для восстановления исходной функции использовался полный набор гармоник от 0-й до 15-й (как показано на предыдущем шаге, этого должно быть достаточно для отличного восстановления). Чтобы более беспристрастно оценивать качество восстановления функции при зашумлении, я дополнительно использовала параметр -s при определении функции из набора гармоник, так как в этом случае выдается график восстановленной функции ЭП без графика исходной функции.

python func2fourier_py3.py func.txt -F 20 -P 20
python fourier-filter_py3.py func_ft.txt -r 0-15
python fourier2func_py3.py func_ft_filtered.txt / python fourier2func_py3.py -s func_ft_filtered.txt

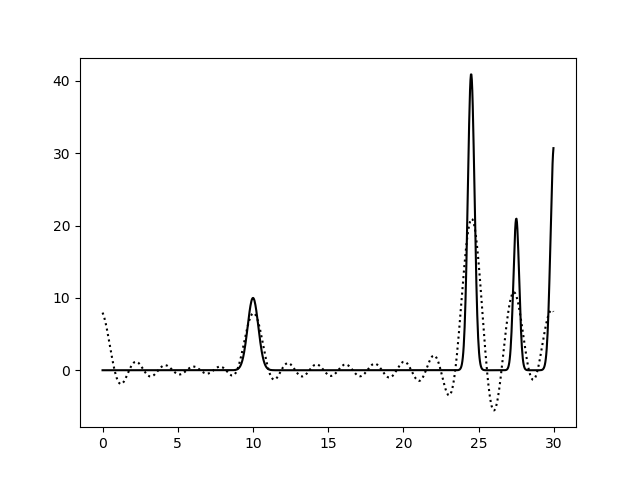
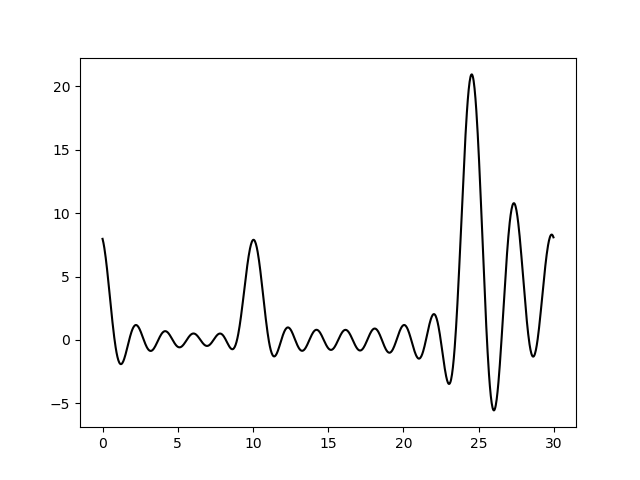
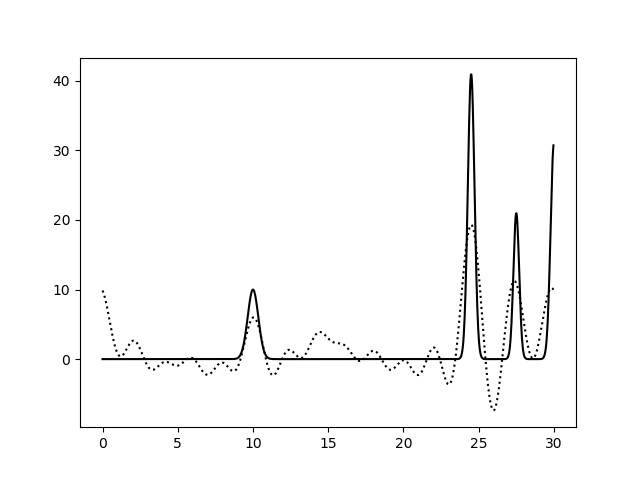
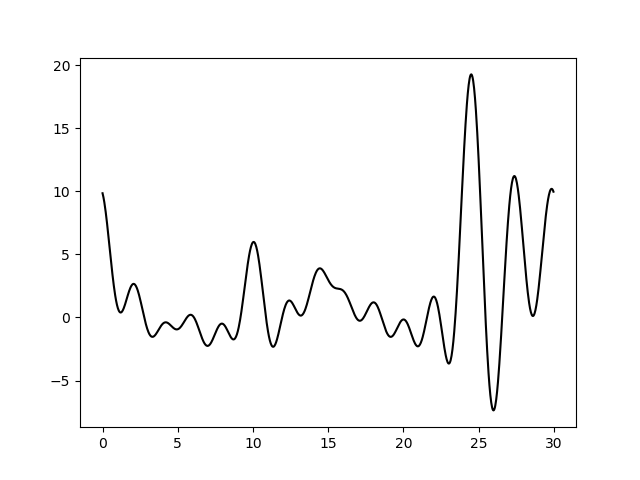
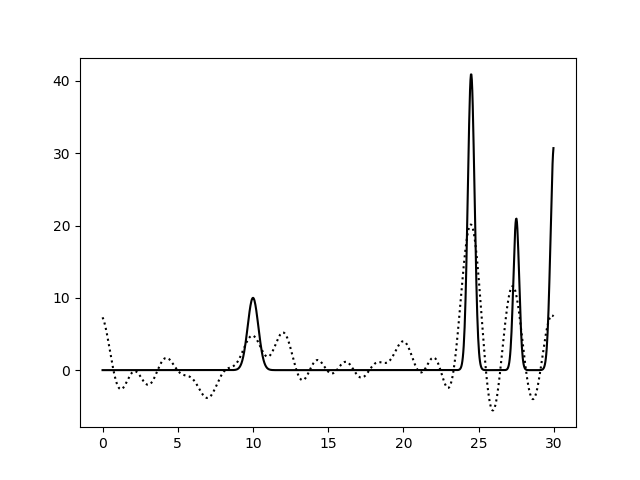
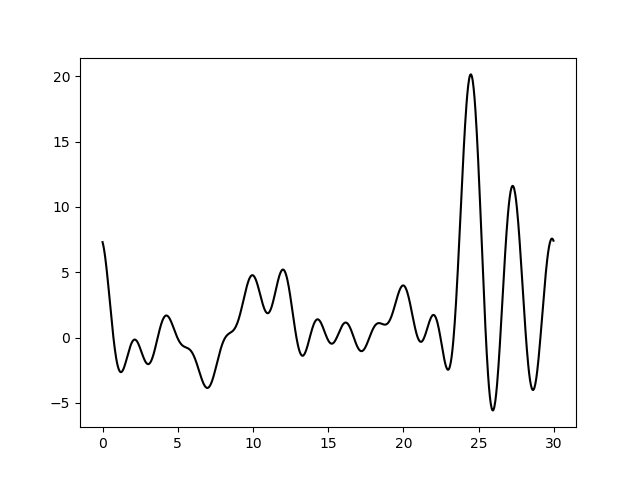
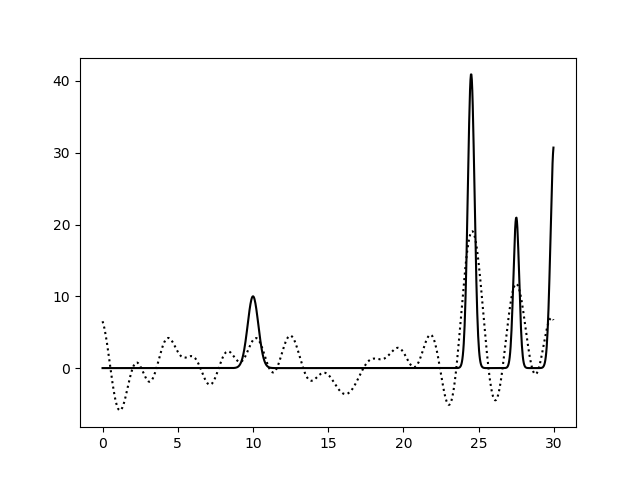
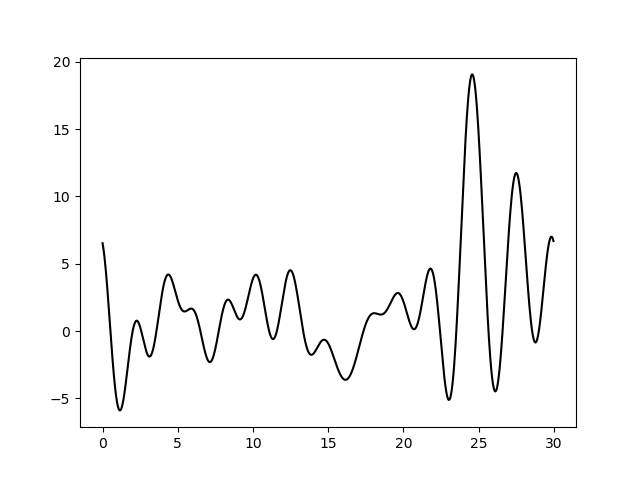
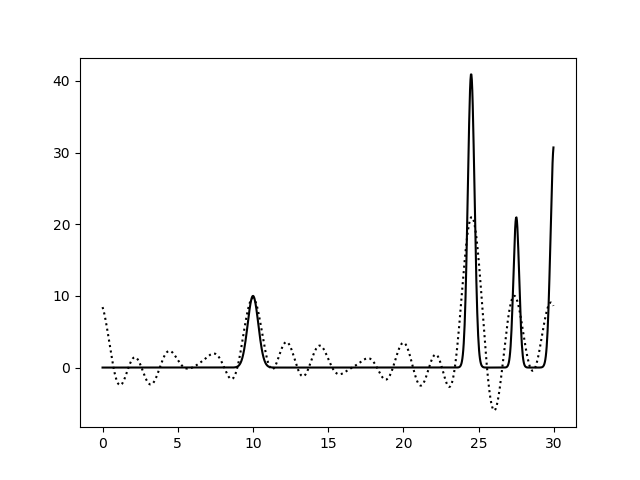
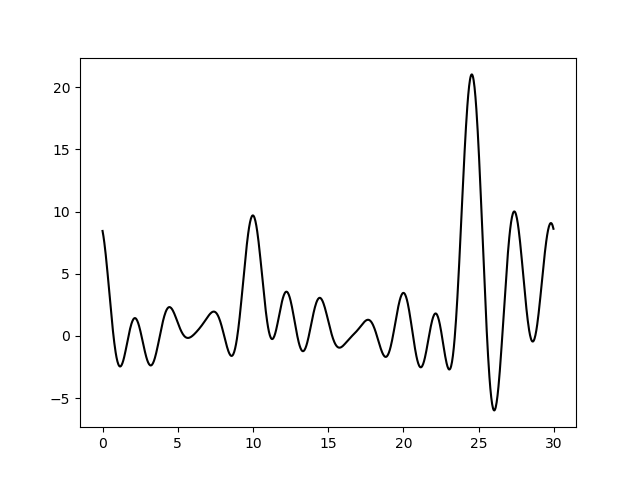
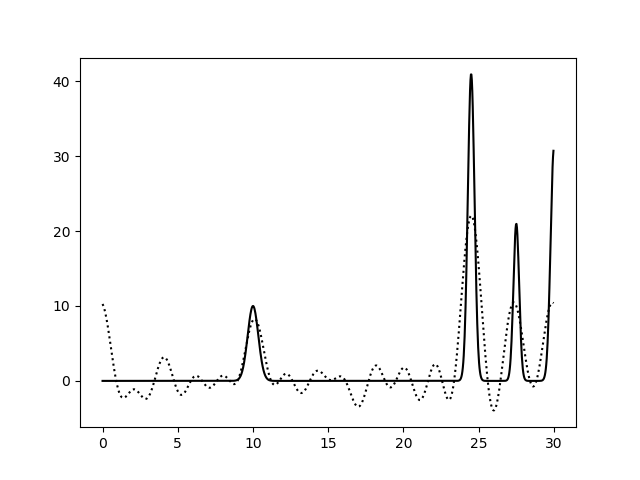
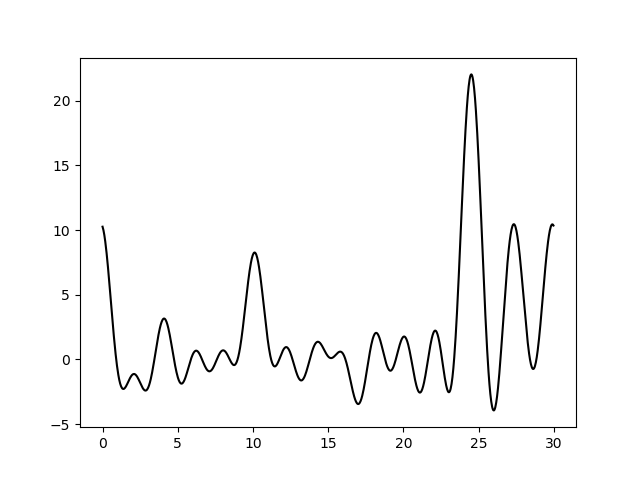
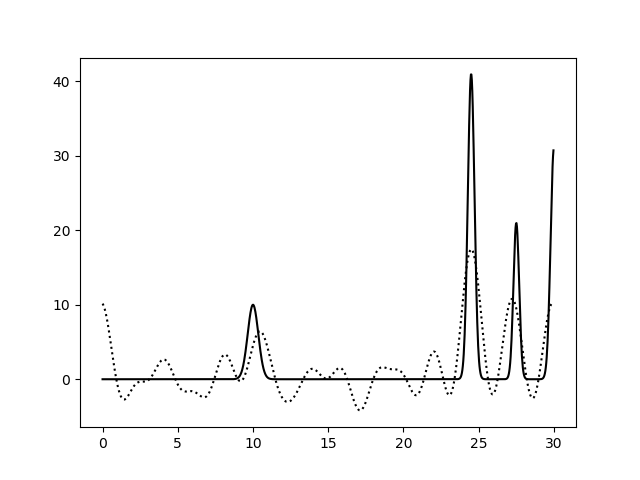
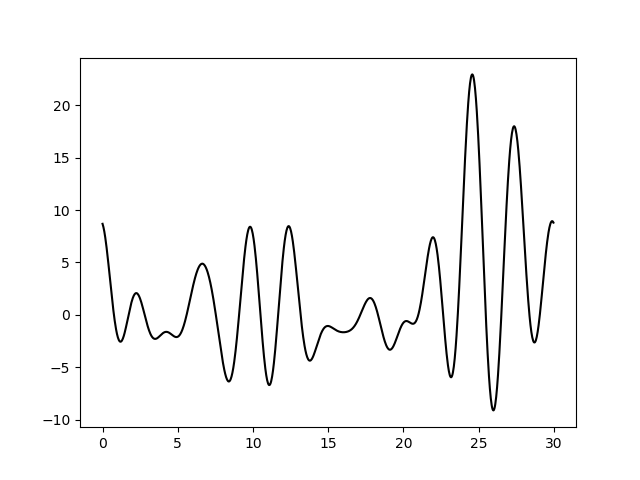
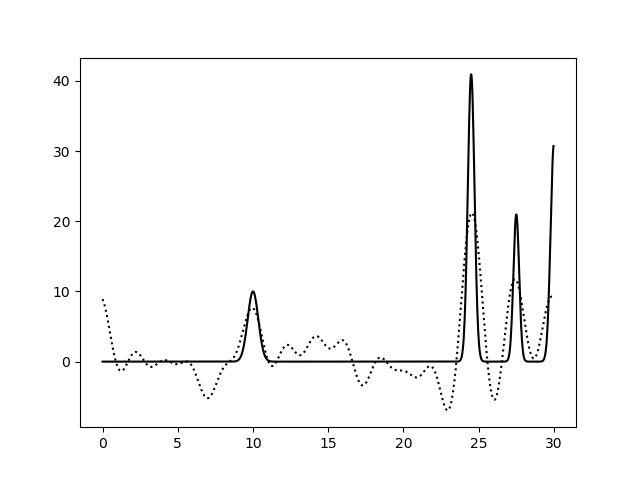
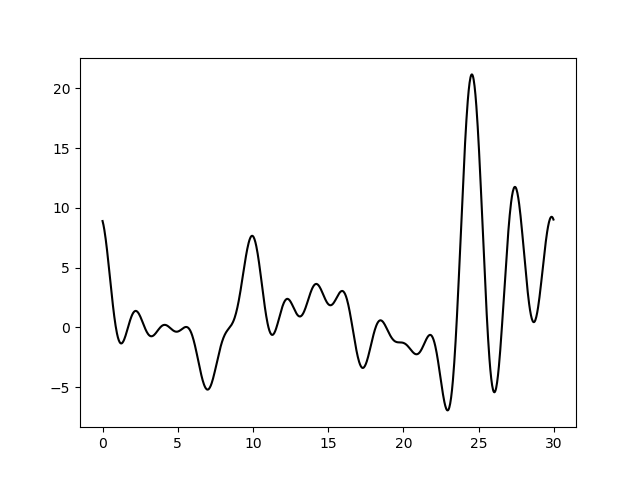
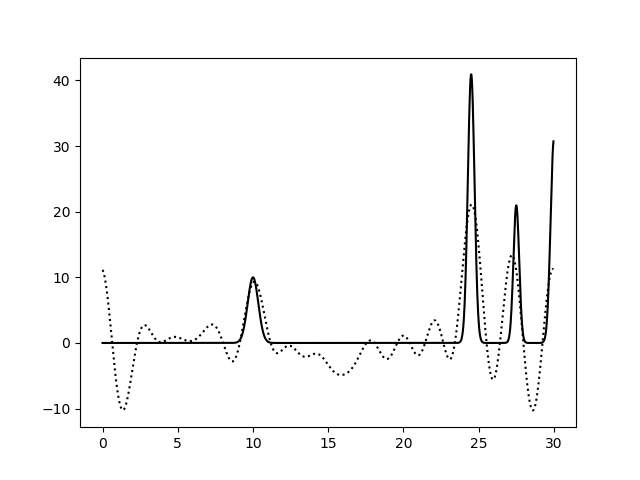
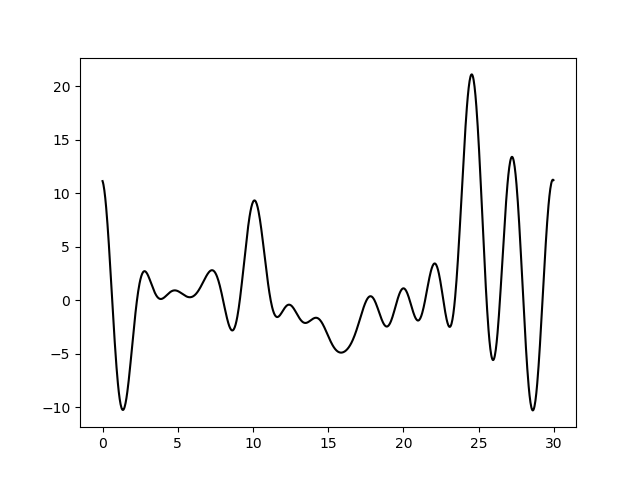
Варьирование этих парамеров показало (см рис 11-19, слева обычное восстановление функции, справа - без визуализации исходной функции), что для точности восстановления исходной функции более принципиально отсутствие шумов в фазах, а не в амплитудах. При F=0 P=20 сигнал не отличим от шума, тогда как при F=35 P=0 вполне отличим. При F=0 P=50 и F=50 P=0 ситуация одинаково плохая - сигнал абсолютно теряется. При этом интересно, что F=20 P=20 и F=35 P=35 выдают картинку в которой пики функции ЭП выделяются, но я думаю, это просто вопрос везения, и на самом деле выводов на основе этих графиков (рис 18-19) делать нельзя.

Рисунок 11.1-11.2. n от 0 до 15, F=0, P=0.

Рисунок 12.1-12.2. n от 0 до 15, F=0, P=20.

Рисунок 13.1-13.2. n от 0 до 15, F=0, P=35.

Рисунок 14.1-14.2. n от 0 до 15, F=0, P=50.

Рисунок 15.1-15.2. n от 0 до 15, F=20, P=0.

Рисунок 16.1-16.2. n от 0 до 15, F=35, P=0.

Рисунок 17.1-17.2. n от 0 до 15, F=50, P=0.

Рисунок 18.1-18.2. n от 0 до 15, F=20, P=20.

Рисунок 19.1-19.2. n от 0 до 15, F=35, P=35.

Восстановление исходной функции ЭП по неполному набору гармоник

Так как в реальном эксперименте не всегда можно найти полный набор гармоник, рассмотрим, насколько хорошо восстанавливается исходная функция ЭП по неполному набору.

Процедура выполнения вычислений стандартная, только на этапе "фильтрации" я попробовала удалить гармоники с самым маленьким, средним и самым большим разрешением (а именно с 0-й по 5-ю, с 5-й по 10-ю и с 10-й по 15-ю). Как и в прошлый раз для более беспристрастной оценки качества восстановления функции использую параметр -s при определении функции из неполного набора гармоник.

python func2fourier_py3.py func.txt -F 20 -P 20
python fourier-filter_py3.py func_ft.txt -r 0-5,10-15
python fourier2func_py3.py func_ft_filtered.txt / python fourier2func_py3.py -s func_ft_filtered.txt

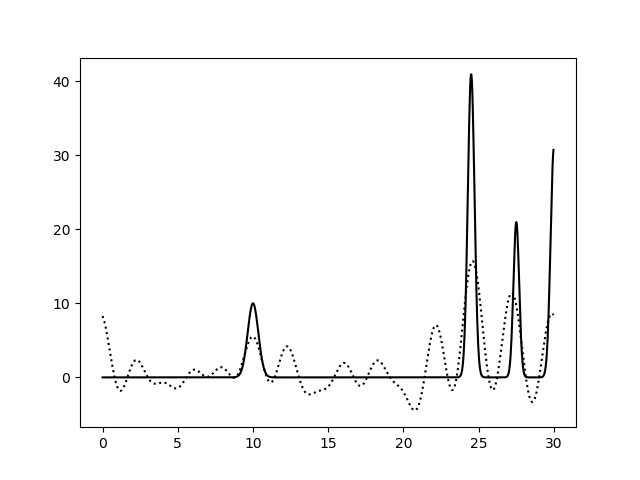
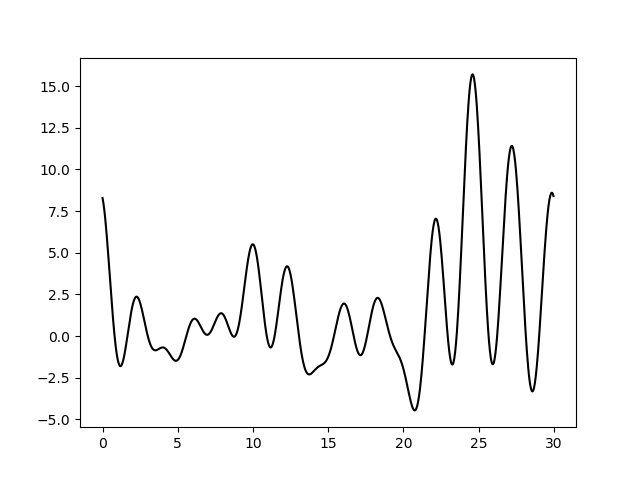
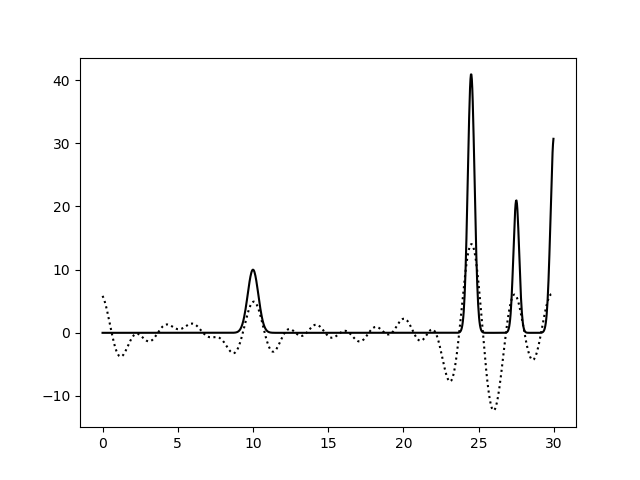
Результат представлен на рисунках 20-23, слева обычное восстановление функции, справа - без визуализации исходной функции. Вопреки ожиданиям, получилось, что для восстановления исходной функции ЭП наиболее важны гармоники со средним разрешением, так как при удалении гармоник с 5-й по 10-ю график становится настолько шумным, что нельзя даже определить положение максимумов. Восстановление функции по набору гармоник от 0-й до 10-й выглядит лучше, чем по набору от 5-й до 15-й, причем, мне кажется, во втором случае то, что мы вообще можем распознать максимумы - дело везения. То есть, видимо, когда в наборе всего 15 гармоник, более важно знать параметры гармоник с низким разрешением.

Рисунок 20.1-20.2. n от 0 до 15.

Рисунок 21.1-21.2. n от 0 до 10.

Рисунок 22.1-22.2. n от 0 до 5 и от 10 до 15.

Рисунок 23.1-23.2. n от 5 до 15.

Итоговая таблица

Разрешение - длина отрезка/номер гармоники. Полнота - количество гарминик в неполном наборе/количество гармоник в полном наборе.

Набор Гармоник Разрешение (A) Полнота (%) Шум Амплитуд (%) Шум Фаз (%) Качество разрешения Комментарий

Полный набор гамоник

0-5 6 100 0 0 Плохое

0-10 3 100 0 0 Хорошее

0-15 2 100 0 0 Отличное

0-20 1.5 100 0 0 Отличное Дальнейшее увеличение количества гармоник не приводит к улучшению восстановления, поэтому остальные итерации в таблице не приводятся.

Полный набор гамоник, добавление гауссовского шума

0-15 2 100 0 20 Среднее Пики расширены, сливаются.

0-15 2 100 0 35 Плохое Пики расширены, сливаются.

0-15 2 100 0 50 Плохое Пики расширены, сливаются.

0-15 2 100 20 0 Отличное Пики довольно четкие.

0-15 2 100 35 0 Отличное Пики довольно четкие.

0-15 2 100 50 0 Плохое Пики соливаются.

0-15 2 100 20 20 Хорошее Пики сливаются, теряется четкая периодичность, однако максимумы неплохо различимы.

0-15 2 100 35 35 Хорошее Пики сливаются, теряется четкая периодичность, однако максимумы неплохо различимы.

Неполный набор гамоник

0-10 3 67 0 0 Хорошее График немного "поплыл".

0-5, 10-15 2 67 0 0 Плохое Хаос пиков.

5-15 2 67 0 0 Среднее Появились пики, обращенные в отрицательную область, но максимумы различимы.

Семестр 7

← Практикум 2 Отчет по валидации →