При кристаллографическом анализе мы получаем на выходе ряд Фурье, по которому восстанавливаем электронную плотность молекулы. В этом практикуме этот процесс приближенно показан на одномерной модели.
Возьмем модель из 5 атомов и приблизительно опишем функцию ее электронной плотности. Я примерно описываю модель H-O-H --- N-C-H, соениненных водородной связью. Одномерная функция ЭП рассчитывается скриптом compile-func.py с параметрами:
python compile-func.py -g 2,3,1+25,3,2+2,3,3+20,3,6+15,3,7.2+2,3,8.3
Где 2,3,1 - высота, ширина и положение пика первой молекулы, и т.д.
Файл с результатом func.txt подается скрипту func2furier.py:
python func2fourier.py -i func.txt -o fourier_full.txt python fourier2func.py -i fourier_full.txt -o func_full.txt
Получилось 498 гармоник. При 498 гармониках восстановленная функция неотличима от изначальной(рис.1.).
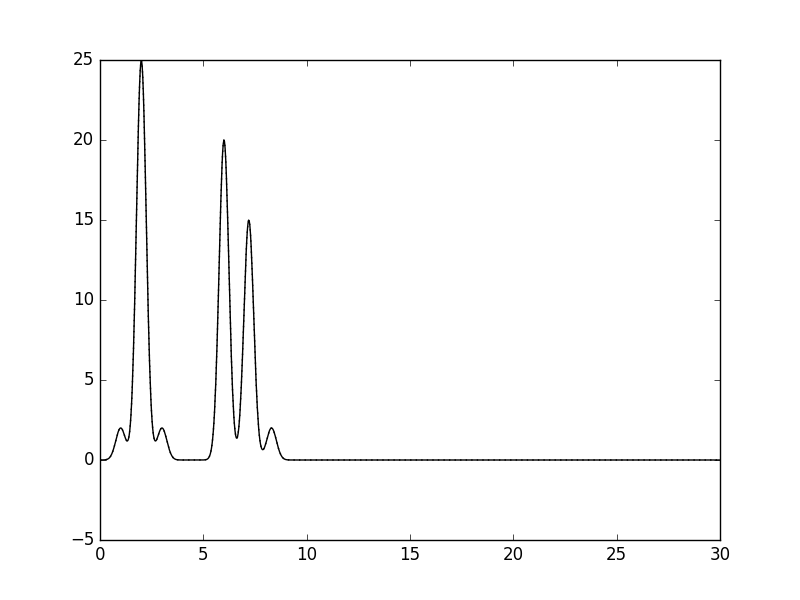
Рис.1. Восстановление функции ЭП по 498 гармоникам.
Однако для хорошего определения функции необязательно иметь все гармоники. На рис.2. приведено наложение восстановленных функций на изначальную. Оценка качества восстановления:
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"
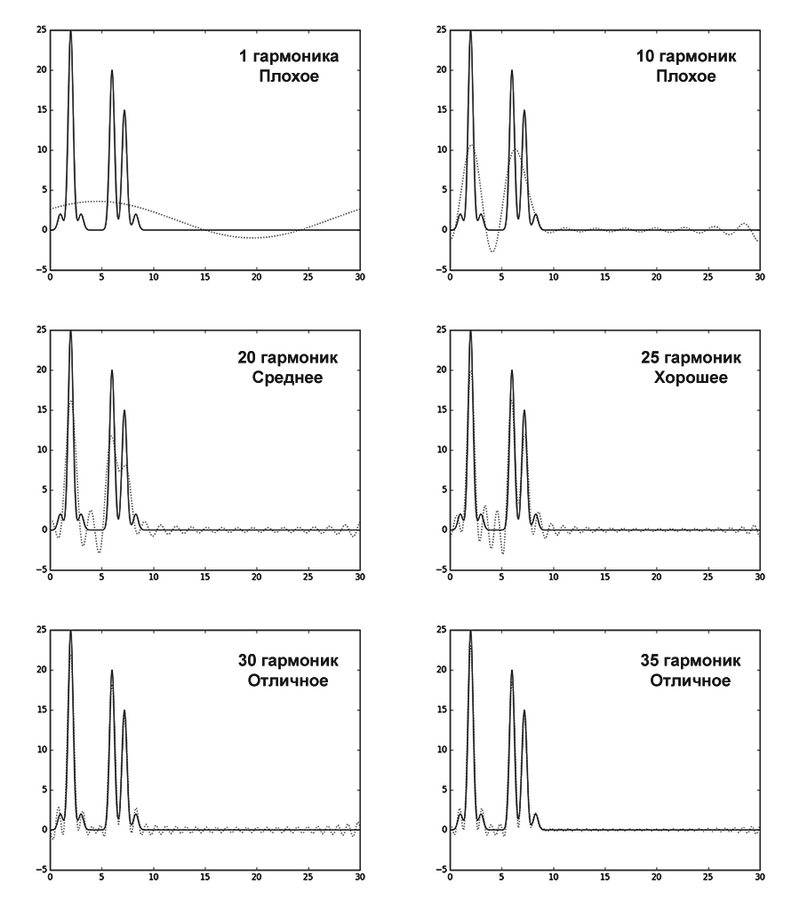
Рис.2. Восстановление функции ЭП по разным количествам гармоник и оценка качества восстановления.
В функцию можно ввести различные шумы, имитируя неточности экспериментального сигнала:
python func2fourier.py -F x -P y -i func.txt -o fourier_noise_.txt
Здесь x - шум, добавленный к амплитудам, y - к фазам. Некоторые варианты представлены на рис. 3:
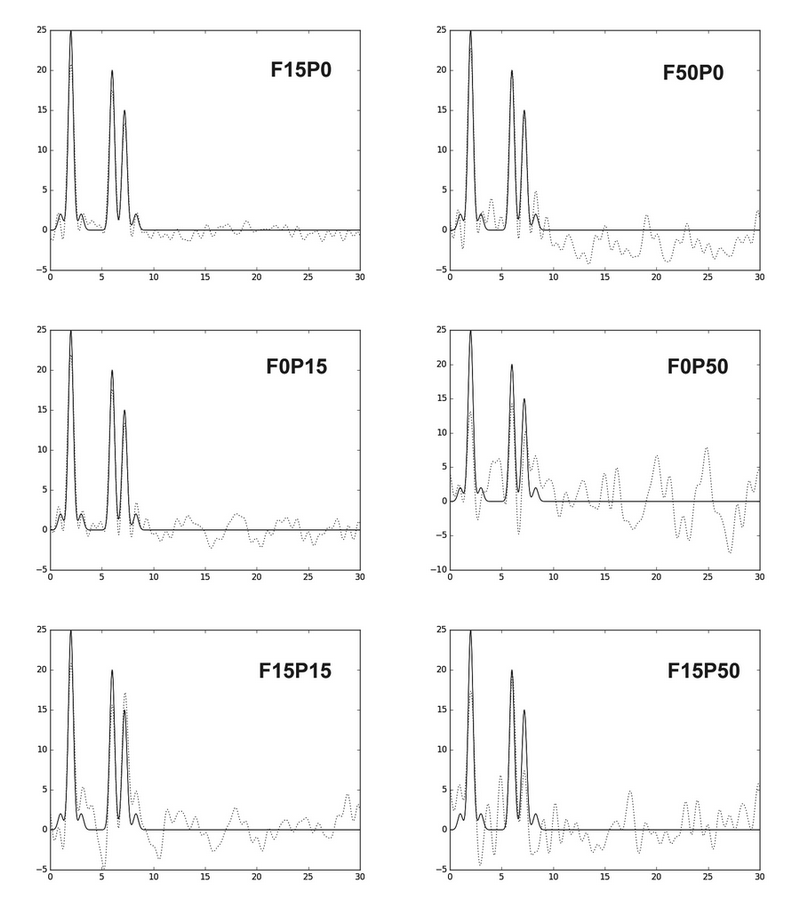
Рис.3. Восстановление функции по 30 гармоникам с различным количеством шума.
Наконец, можно восстанавливать функцию по неполному набору гармоник. Если удалить первую гармонику (рис.4, б), функция все еще хорошего качества, но "искривляется", повторяя форму первой гармоники. Если удалить гармоники из середины (рис.4, в), то появляются частые колебания, мешающие четко различить пики. Если же добавить более позднюю гармонику (рис.4, г), не будет заметный отличий.
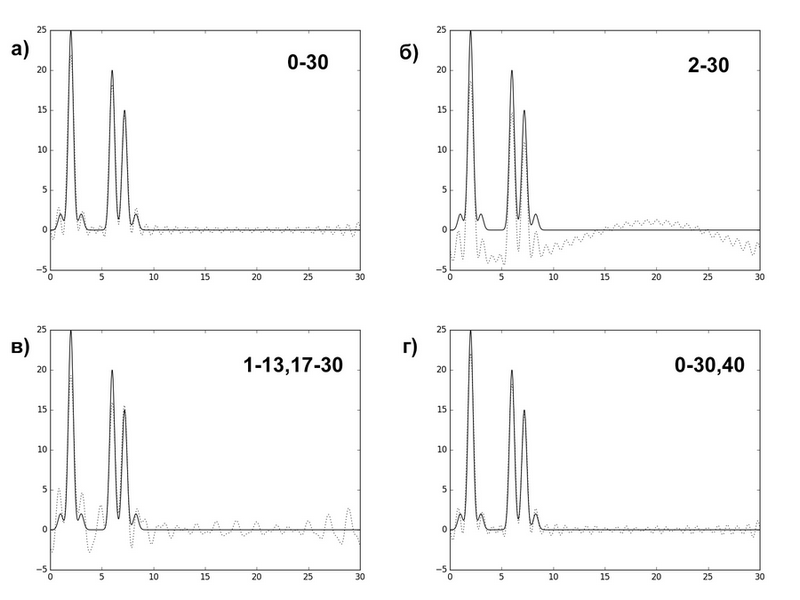
Рис.4. Восстановление функции по неполному количеству гармоник.
Таблица 1. Восстановление функции по коэффициентам ряда Фурье.
|
Набор гармоник |
Разрешение (A) |
Полнота данных (%) |
Шум амплитуды (% от величины F) |
Шум фазы (% от величины phi) |
Качество восстановления (отличное, хорошее, среднее, плохое) |
Комментарии |
|
Полный набор гармоник |
||||||
|
0–1 |
30 A |
100% |
0 |
0 |
Плохое |
|
|
0–10 |
3 A |
100% |
0 |
0 |
Плохое |
|
|
0–20 |
1.5 A |
100% |
0 |
0 |
Среднее |
|
|
0-25 |
1.2 |
100% |
0 |
0 |
Хорошее |
|
|
0-30 |
1 |
100% |
0 |
0 |
Отличное |
|
|
0-30 |
1 |
100% |
15 |
0 |
Хорошее |
|
|
0-30 |
1 |
100% |
50 |
0 |
Среднее |
|
|
0-30 |
1 |
100% |
0 |
15 |
Хорошее |
|
|
0-30 |
1 |
100% |
0 |
50 |
Среднее |
|
|
0-30 |
1 |
100% |
15 |
15 |
Среднее |
|
|
0-30 |
1 |
100% |
15 |
50 |
Среднее |
|
|
0-35 |
0.86 |
100% |
0 |
0 |
Отличное |
|
|
Неполный набор гармоник |
||||||
|
2–30 |
1 |
93% |
0 |
0 |
Отличное |
|
|
1–13,17-30 |
1 |
83% |
0 |
0 |
Среднее |
|
|
0-30, 40 |
0.75 |
100% |
0 |
0 |
Отличное |
|