Филогенетическое дерево и его реконструкция

Скобочная формула, задающая гипотетическую модель эволюции гена, имеет следующий вид:

Используя эту формулу, вручную в графическом редакторе Paint создали изображение соответствующего ей филогенетического дерева. Заметим, что это укорененное дерево. Красным отмечены внутренние ветви (см.следующее упражнение)

Расстояние до разных листьев может быть разной длины (обратим внимание на кладу CDE), поскольку в качестве эволюционного расстояния, отраженного длиной ветвей, в нашей модели фигурирует число мутаций (замен), а не время эволюции.

В любом бинарном неукорененном дереве, содержащем N листьев, всегда имеется 2N–3 ветви. Следовательно, в дереве из шести листьев будет 9 ветвей, из них шесть внешних ветвей и три внутренних. Внешние ветви соединяют какой-либо лист с остальными элементами дерева; такие ветви описываются тривиально, и они есть в любом дереве из шести листьев, поэтому соответствующие разбиения здесь не приводятся. Каждая внутренняя ветвь разбивает множество всех листьев дерева, в нашем случае множество ABCDEF, на два подмножества - листьев, расположенных с одного и с другого конца ветви. Ниже приведено описание ветвей дерева из упражнения 1 в виде таблицы разбиений множества листьев каждой ветвью. Точками обозначены ветви, принадлежащие одному подмножеству, звездочками - другому (не важно, какому). Заметим, что наше дерево укорененное, поэтому в нем появляется еще один узел - корень. а также еще одна внутренняя ветвь (см.красные ветви на иллюстрации к упражнению 1)

Листья  A B C D E F
Ветви
1     .  . * * * *
2     .  . * * * .
3     .  . . * * .
4     .  . . . . *

Применим модель эволюции, описанную скобочной формулой в упражнении 1, к прокариотическому гену aspC. Для этого с помощью программы msbar создадим мутантные последовательности, соответствующие всем узлам и листьям дерева в том порядке, какой диктует нам направление эволюции. К примеру, чтобы "создать" мутанта A, сначала получим через msbar последовательность некоего общего для A и B предка, а потом только из него получим A, а не внесем сразу все мутации в последовательность aspC. В нашей скобочной формуле расстояния, отделяющее одну последовательность от другой, даны в количестве замен на одну сотню нуклеотидов. Для работы с msbar требуется задать абсолютное число замен в последовательности. Ген aspC имеет длину 1331 нуклеотид. Поэтому приведенные в скобочной формуле числа умножим на 1331 и разделим на 100. Полученные результаты округлим до целого (число замен не может быть дробным). Абсолютные количества замен используем при написании скрипта, в результате работы которого получается файл со всеми мутантными последовательностями (только A,B,C,D,E,F, но не последовательности узлов и не исходный ген!). Текст скрипта можно посмотреть, щелкнув сюда. Добавим, что в полученном файле ABCDEF мы вручную изменили названия последовательностей на необходимые (A-F).

Полученный в предыдущем упражнении файл ABCDEF.fasta подадим на вход трем программам, реализующим различные алгоритмы реконструкции филогенетических деревьев. Для создания дерева по набору последовательностей методом максимального правдоподобия (AML - Analysis by Maximum Likelihood) используем программу fdnaml. Для ее работы не требуется предварительныого вычисления матрицы попарных расстояний; программа реконструирует неукорененное дерево следующего вида:

+--------------B | | +----------------------------------F | | 1--------------4 +-------E | | +------3 | +-------------2 +---------D | | | +---------C | +--------A

Другими двумя алгоритмами реконструкции деревьев мы уже пользовались во втором семестре (см.отчет по практикуму "Филогенетические деревья, реконструированные разными способами". Это алгоритмы UPGMA и Neighbor-joining; первый строит укорененные деревья, второй - неукорененные. Оба алгоритма алгоритмов работают только с матрицей попарных расстояний, поэтому их использование требует сначала подсчета попарных расстояний между последовательностями с помощью программы fdnadist.

Linux-реализацией пакета Phylip мы пользуемся впервые; оба алгоритма "зашиты" в одну программу fneighbor, вид алгоритма задается значением параметра treetype (UPGMA - u; Neighbor-joining - по умолчанию - n). Полученные деревья имеют следующий вид:

+--------------B ! ! +-----------------------------------F 1--------------2 ! ! +--------C ! +---------------3 ! ! +---------D ! +-------4 ! +--------E ! +-------A

                       +-----------A         
      +----------------2 
      !                +-----------B         
  +---4 
  !   !              +------------C         
  !   +--------------3 
--5                  !    +--------D         
  !                  +----1 
  !                       +--------E         
  ! 
  +-------------------------------F          


Использование параметра ttratio
При получении деревьев с помощью трех перечисленных выше алгоритмов мы не меняли никаких параметров программ fdnaml и fdnadist,
кроме параметра  ttratio. Данная опция, судя по справкам к названным программам, означает отношение числа транзиций к числу
трансверсий в
последовательностях, поданных на вход. По умолчанию значение ttratio равно двум, так как в природе мутации по типу транзиций
встречаются чаще (транзиция - смена основания на однотипное - пурин на пурин, пиримидин на пиримидин, такая замена
слабее меняет геометрию спирали ДНК, чем трансверсия - замена на основание другого типа; по этой причине
трансверсии реже обнаруживаются репарационными системами клетки и реже элиминируются). Однако происхождение наших мутантых
последовательностей, соответствующих листьям
дерева из упражнения 1, - искусственное. Они были созданы из последовательности гена aspC с помощью программы msbar.
Последняя делает замены в последовательности случайным образом, не отличая транзиции от трансверсии, поэтому в мутантах число
тех и других замен примерно одинаково.
По данной причине мы изменили значение параметра ttratio, сделав его равным 1; такое значение больше соответствует
действительности, что обещает меньше ошибок при реконструкции дерева. 


Анализ деревьев, полученных с помощью различных методов.

При выполнении предыдущих заданий мы получили четыре дерева: одно нарисовали "вручную" по скобочной формуле,
еще три получили с помощью различных алгоритмов реконструкции по набору мутатных последовательностей, созданных согласно
той же скобочной формуле. Сначала сравним эти деревья между собой, особенно уделяя внимание тому, насколько
реконструированные деревья соответствуют
первому - "правильному" с точки зрения заданной скобочной формулы. Для этого воспользуемся стандартной процедурой сравнения ветвей
деревьев как разбиений множеств их
листьев (см. упражнение 2).





  A B C D E F  Дерево "вручную" Дерево методом AML  Дерево Neighbor-Joining  Дерево UPGMA
Тип дерева        укорененное     неукорененное         неукорененное         укорененное
Ветви
1 . . * * * *        +               +                       +                 +
2 . . * * * .        +               +                       +                 +
3 . . . * * .        +               +                       +                 +      
4 . . . . . *        +               -                       -                 +
       


         
       
Как видно из таблицы, деревья схожи между собой тем, чтовсе имеют ветви 1,2 и 3.Однако в укорененных деревьях есть одна
дополнительная ветвь 4. Объяснение этому
факту дано в упражнении 1: при укоренении в структуре дерева появляется дополнительный
узел (корень), и, соответственно, дополнительная ветвь. Однако большого значения при сравнении деревьев это не имеет
(укоренить можно любое неукорененное 
дерево), поэтому можно сказать, что все деревья сходны, то есть алгоритмы AML, UPGMA и Neighbor-Joining
реконструировали деревья, соответствующие "правильному".
Тем не менее, каждое из деревьев имеет свои особенности. Деревья, построенные с помощью метода максимального правдоподобия
и Neighbor-joining, очень схожи, отличаются только длиной некоторых ветвей. Это неукорененные деревья, в которых расстояние от
узла до разных ветвей клады, "растущей" из этого узла, может быть разным, что не соответствует теории молекулярныхчасов, но
согласуется с нашей моделью,
где эволюционное расстояние суть число мутаций. Дерево, постренное алгоритмом UPGMA укорененное и
ультраметрическое, то есть расстояние от корня до любой из ветвей, судя по изображению дерева, одинаковое. "Содержательно
ультраметрические деревья соответствуют случаю,
когда длины ветвей суть время эволюции" (презентация ко второй лекции по биоинформатике); но это не наш случай, поэтому
UPGMA-реконструкция кажется не самой удачной. Заметим, что некоторые особенности правильного дерева не отражены в
реконструированных. К примеру, на самом деле расстояние от общего предка AB до A равно расстоянию до B,
однако неукорененные деревья (AML и NJ) отображают ветви клады AB как ветви разной длины. Такие погрешности можно связать со
случайными событиями при "мутировании" с помощью msbar. Обе последовательности - A и B - создавались из одной (AB), при этом было
произведено одинаковое число замен. Однако число однотипных замен (например, G на G) и замен в том же сайте (G на C, а потом опять 
на G или другой нуклеотид) могло быть разным, что отразилось на эволюционных расстояниях, визуализируемых длиной ветвей дерева.
Бутстреп-анализ выравнивания мутированных последовательностей A,B,C,D,E и F.
В отчете по этому упражнению опишите, совпало ли консенсусное дерево по топологии с реальным деревом, а также каковы
бутстреп-значения внутренних ветвей консенсусного и реального деревьев.
Проиллюстрируйте свои выводы выдержками из выходного файла. 

Визуализация скобочных формул с помощью fdrawtree.

С Online-версией пакета Phylip мы знакомились во втором семестре; в том числе с программами-визуализаторами drawtree и drawgram.
Сейчас, в порядке ознакомления с Linux-версией того же пакета создадим изображение полученного в прошлом упражнении дерева
с помощью fdrawtree. Эта программа визуализирует данную на вход скобочную формулу в виде неукорененного дерева в
Postscript-формате. В результате получаем такое изображение:

Рисунок. Консенсусное дерево, визуализированное с помощью fdrawtree.



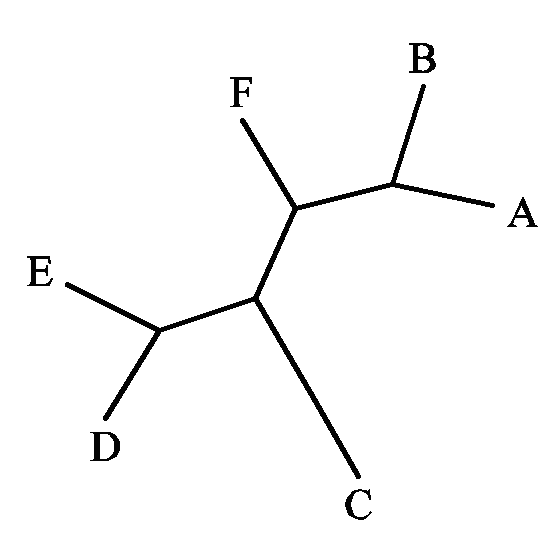
Для интереса воспользуемся и Linux-аналогом программы drawgram - fdrawgram. Эта программа строит укорененные деревья.
Вот что мы получили,
подав ей на вход скобочную формулу из файла consensus.treefile (см. прошлое упражнение).
Рисунок. Консенсусное дерево, визуализированное с помощью fdrawgram.