Электронная плотность

Задание функции

Для компьютерного эксперимента использовалась следующая модель:

* Функция имеет вид нескольких гауссовых кривых с центром в разных точках (например, на расстоянии 1-1.5Å — модель ковалентно связанных атомов).

Для создания функции использовался скрипт compile-func.py: 
 python compile-func.py -g 2,3,3.1+32,3,4.2+8,3,5.3+24,3,10.1+34,3,11.5
В результате был получен файл func.txt с координатами точек и изображение смоделированной функции:

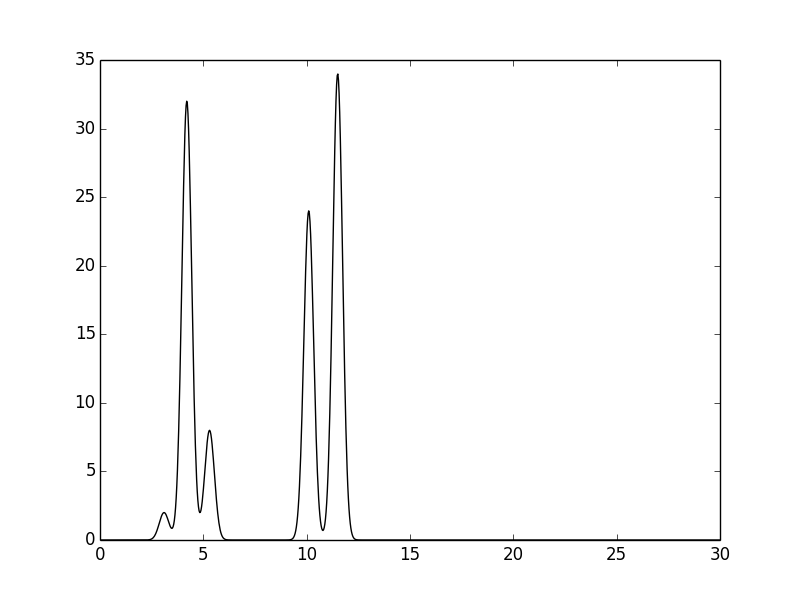
Расчет амплитуд и фаз сигналов

Амплитуды и фазы рассчитываются по созданной функции ЭП. При этом учитывается, что в эксперименте определяются амплитуды не для всех сигналов, что интенсивности сигналов и амплитуды определяются с ошибкой и что фазы определятся для всех измененных сигналов с ошибкой.
Для разложения функции ЭП здесь и далее использовался скрипт func2fourier.py, на вход которому подается файл func.txt и (опционально) значения гауссовского шума. В результате был получен файл func_ft.txt, имеющий формат <номер гармоники> <амплитуда> <фаза> и содержащий 499 гармоник. Для восстановления исходной ЭП используется скрипт fourier2func.py.

Влияние количества гармоник

Сначала для файла без шума был произведен отбор гармоник от 0 до n-й (5 < n < 45) с помощью скрипта fourier-filter.py и затем для каждого набора была восстановлена функция ЭП: 
 python func2fourier.py -i func.txt
 python fourier-filter.py -r 0-n
 python fourier2func.py -f func.txt -i func_ft_filtered.txt
Результаты представлены на рисунках ниже. Видно, что при n = 30 положение атомов уже определяется достаточно однозначно, однако я решила взять немного больше гармоник, чтобы избежать сильных шумов (n=40).

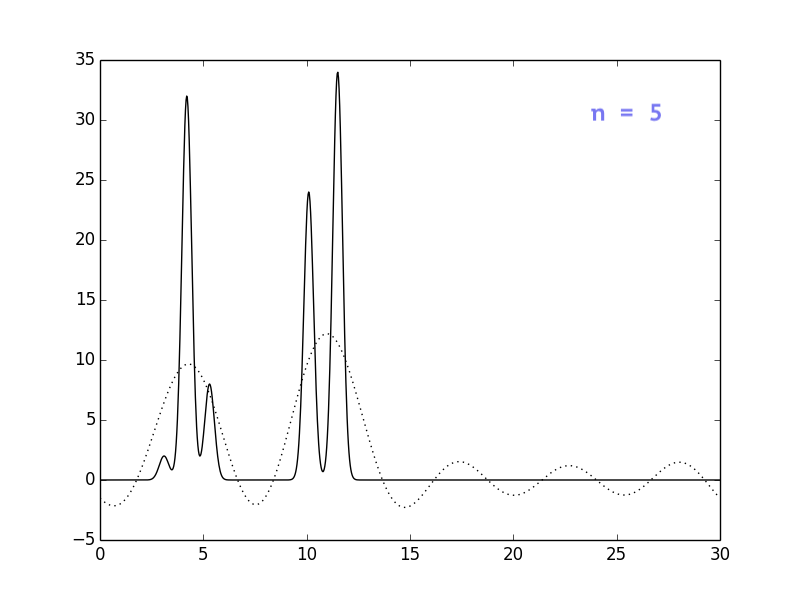
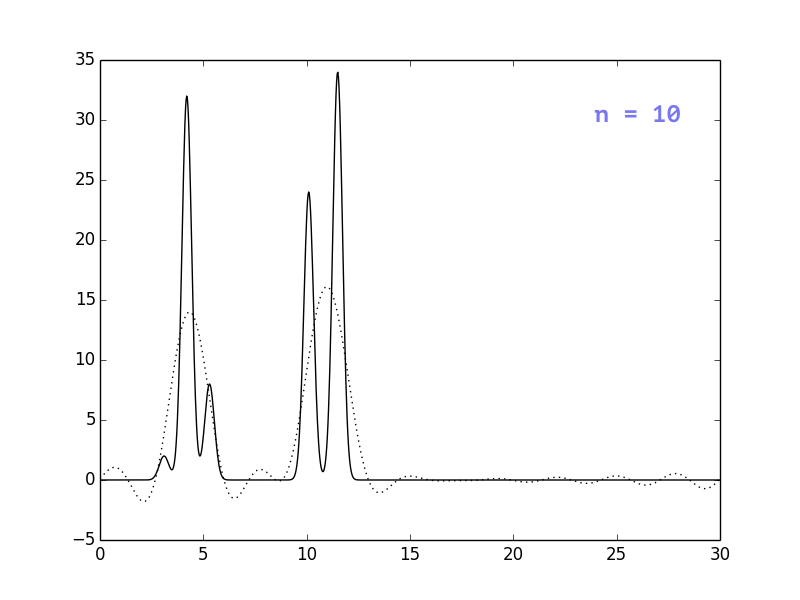
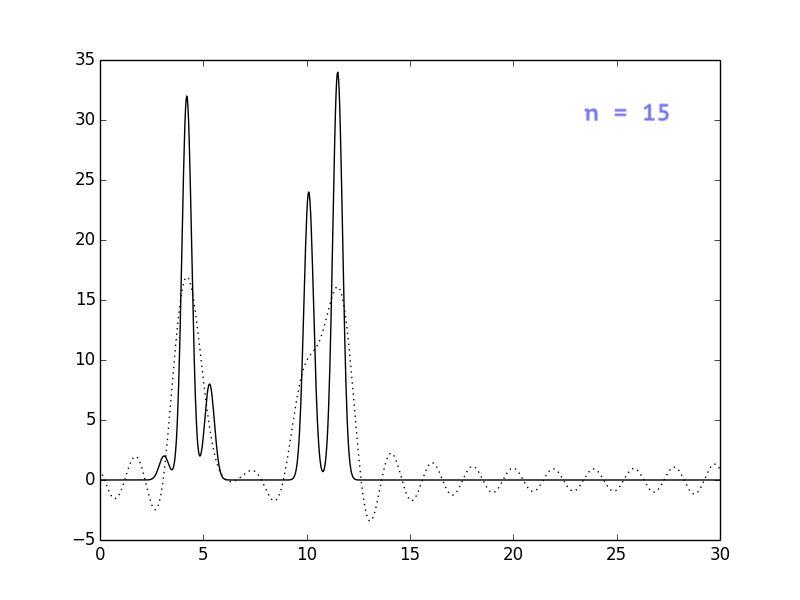
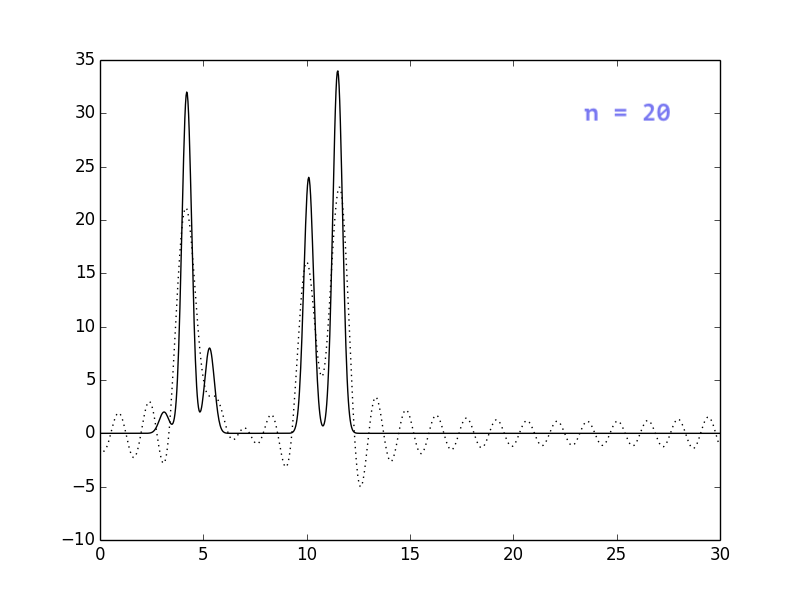
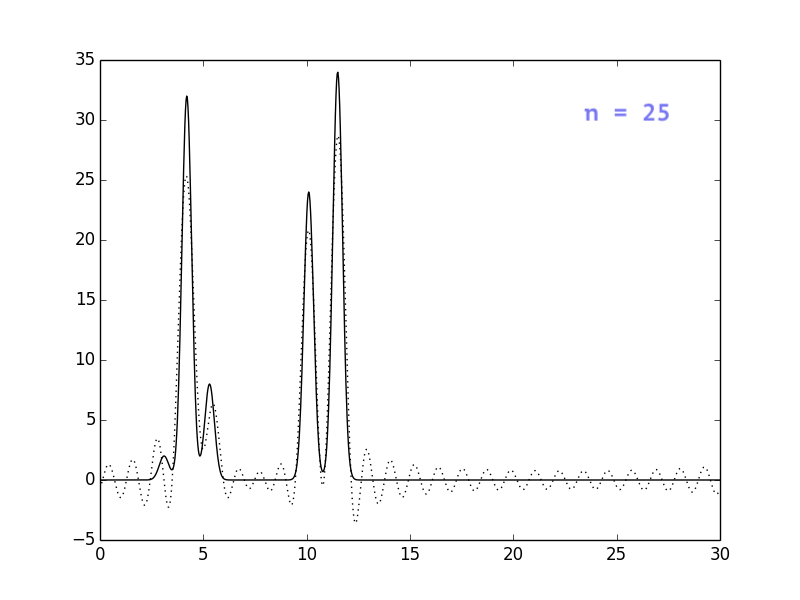
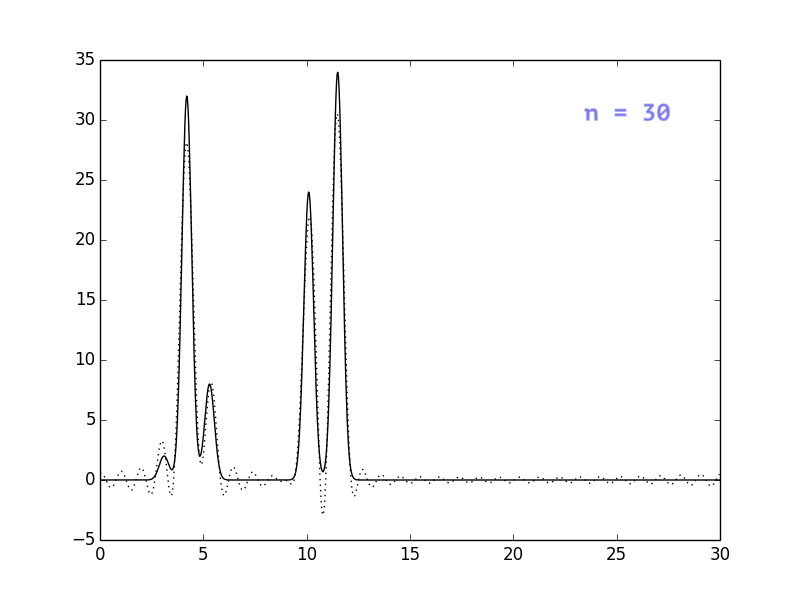
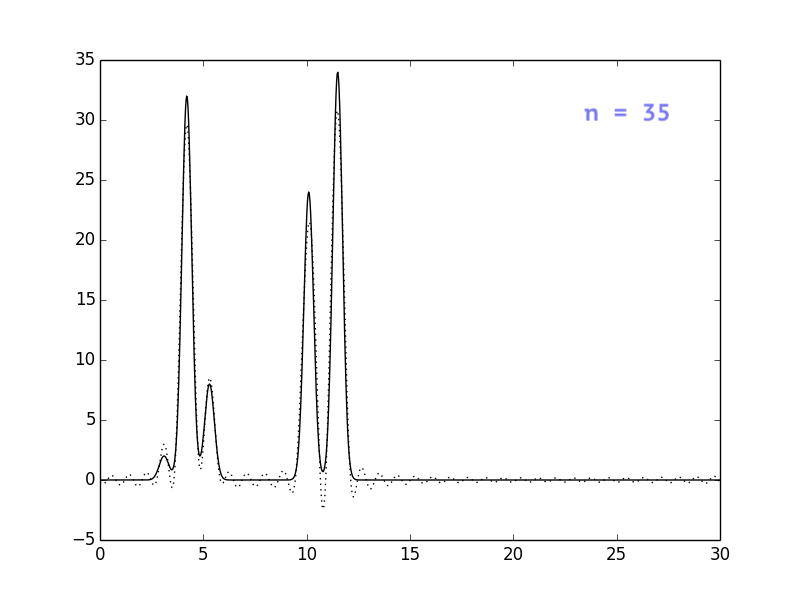
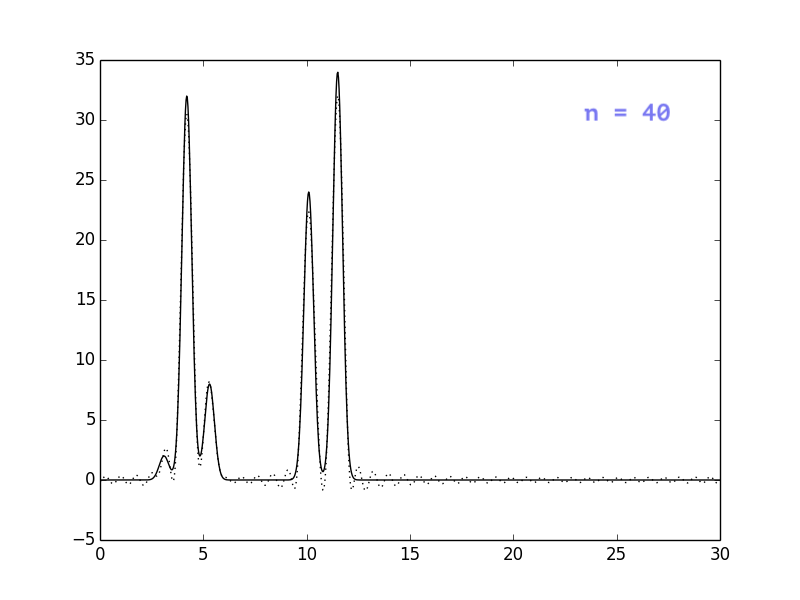
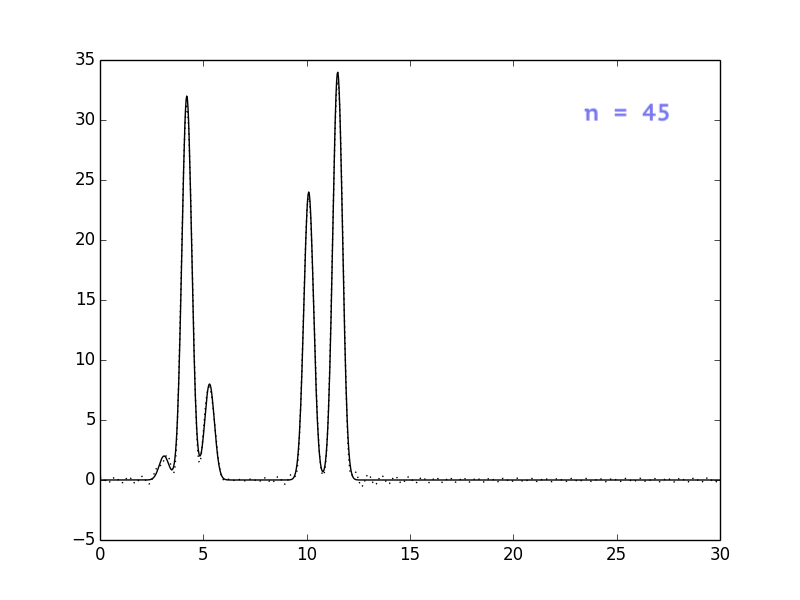
Влияние шумов

Было проанализировано влияние гауссовского шума, добавленного к амплитуде и фазе как по отдельности, так и одновременно. Для этого использовались команды: 
 python func2fourier.py -i func.txt -F % -P %
 python fourier-filter.py -r 0-40
 python fourier2func.py -f func.txt -i func_ft_filtered.txt
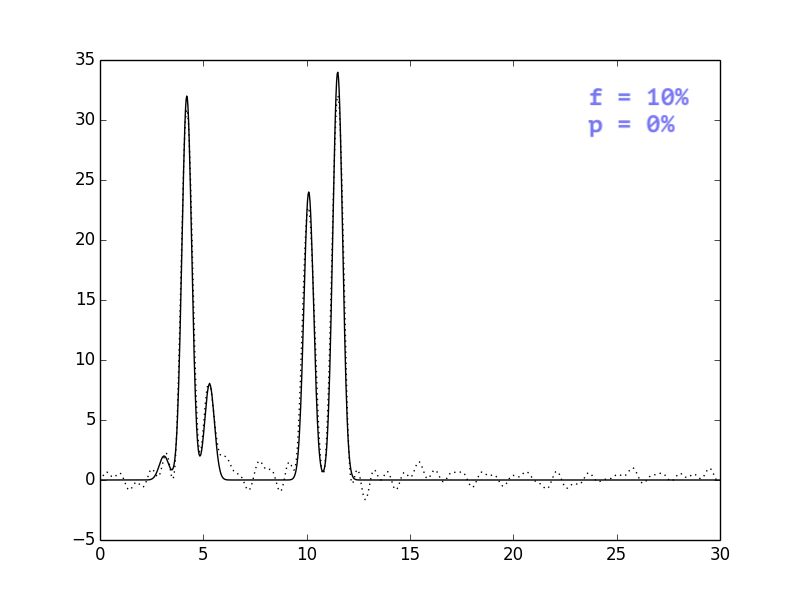
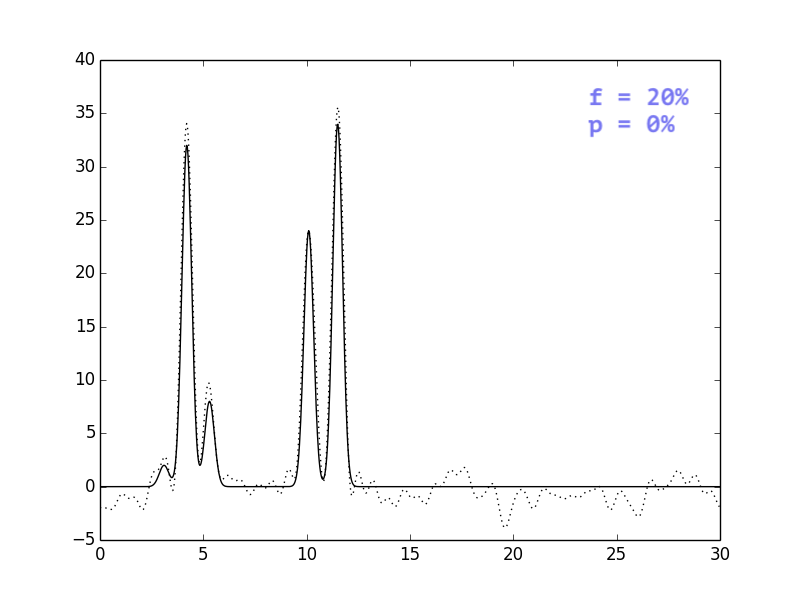
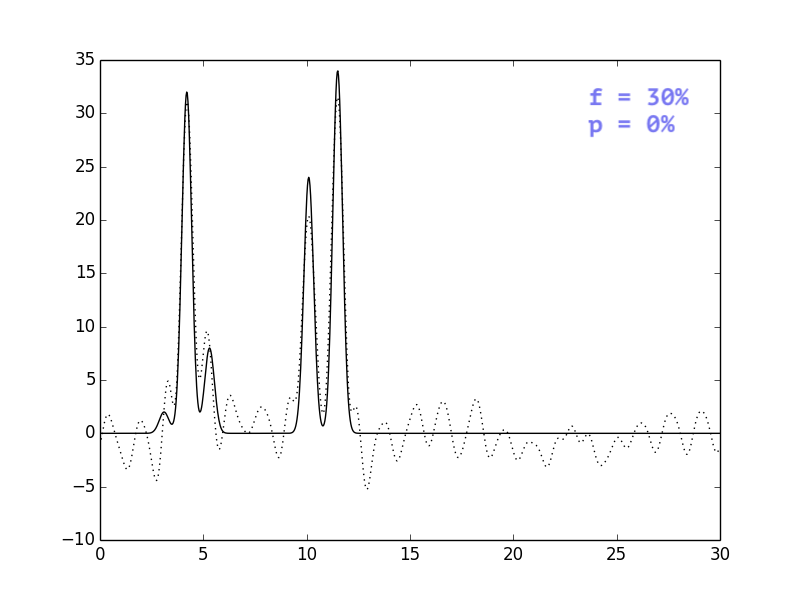
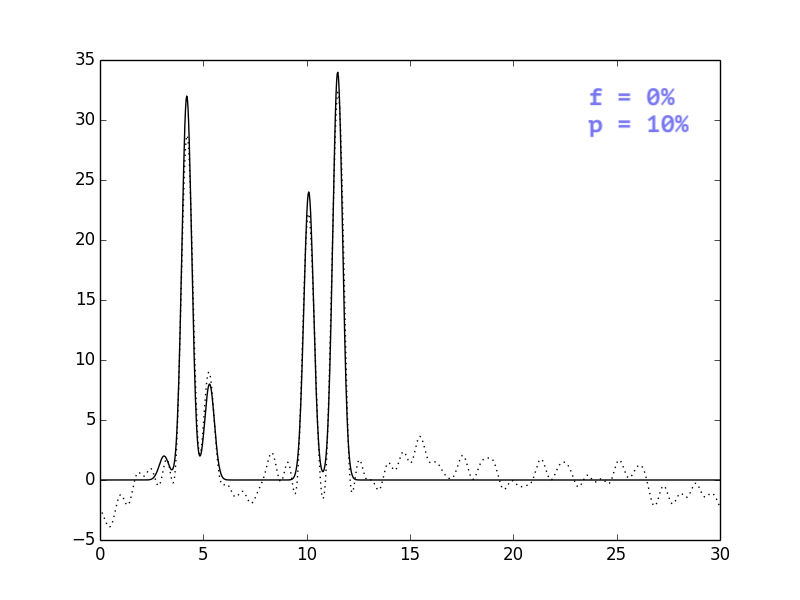
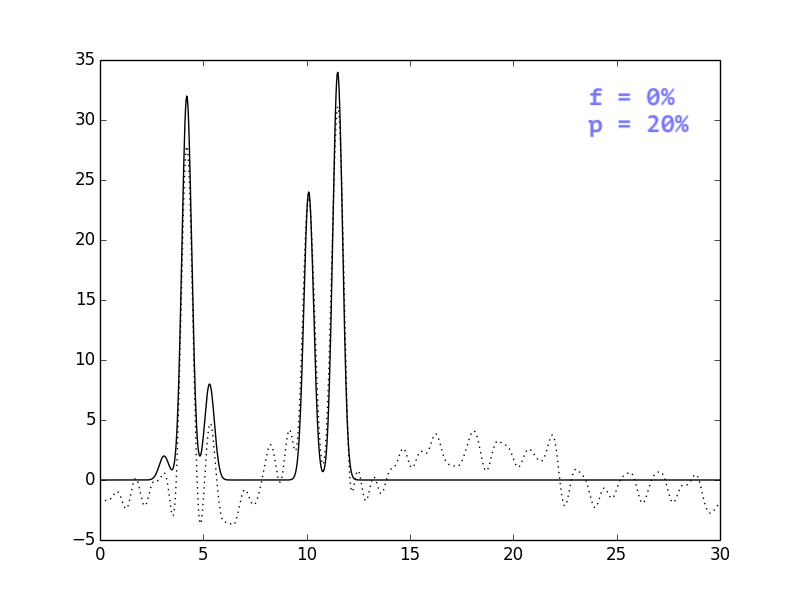
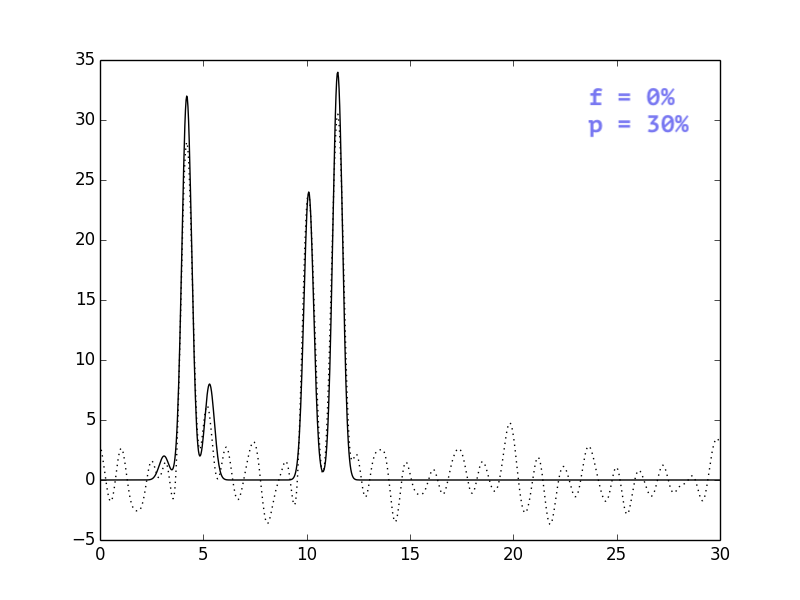
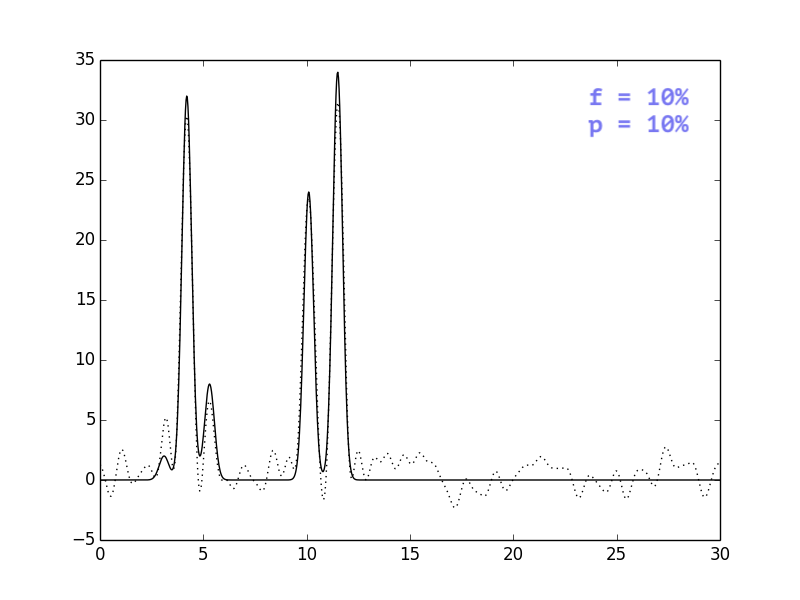
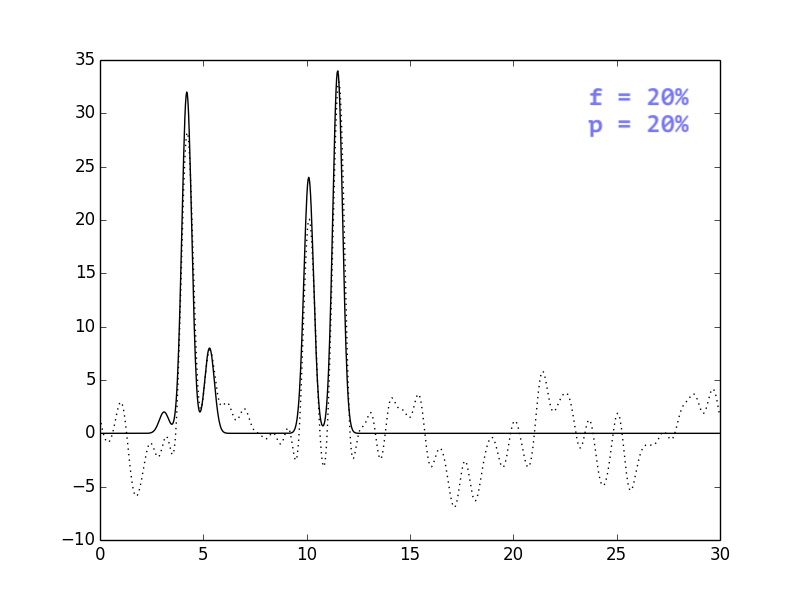
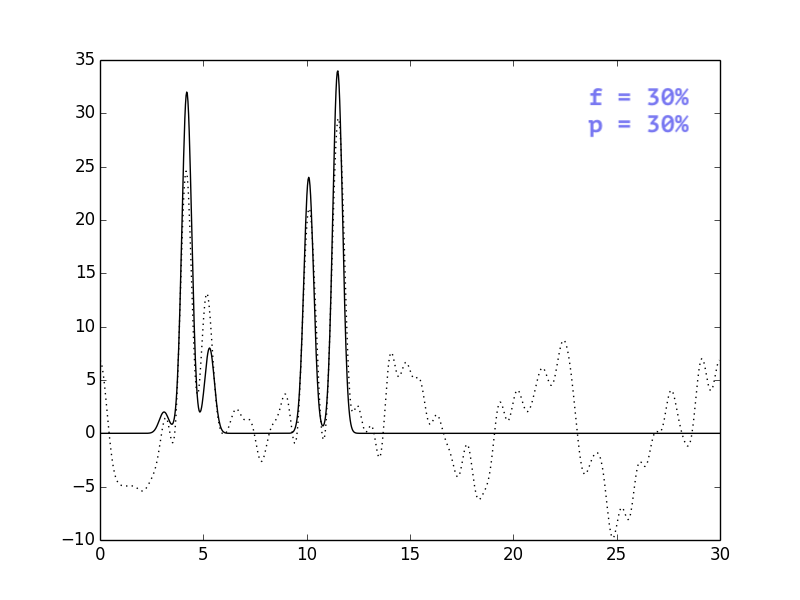
В целом, выводы тривиальны: i) добавление шума одновременно и к амплитудам, и к фазам ухудшает восстановление сильнее, чем добавление шума только к одному из параметров; ii) чем сильнее шум, тем больше ошибочных пиков, которые могут быть приняты за сигнал.

Влияние полноты набора

Часто в результате эксперимента имеется неполный набор гармоник. Для моделирования этой ситуации были использован исходный набор из 499 гармоник, из которого выборочно брались разные множества гармоник с помощью уже упоминавшихся скриптов: 
 python func2fourier.py -i func.txt 		# используется 1 раз, чтобы
						# получить набор без шума 
 python fourier-filter.py -r 0-25,30-40
 python fourier2func.py -f func.txt -i func_ft_filtered.txt
Результаты представлены на рисунках ниже:

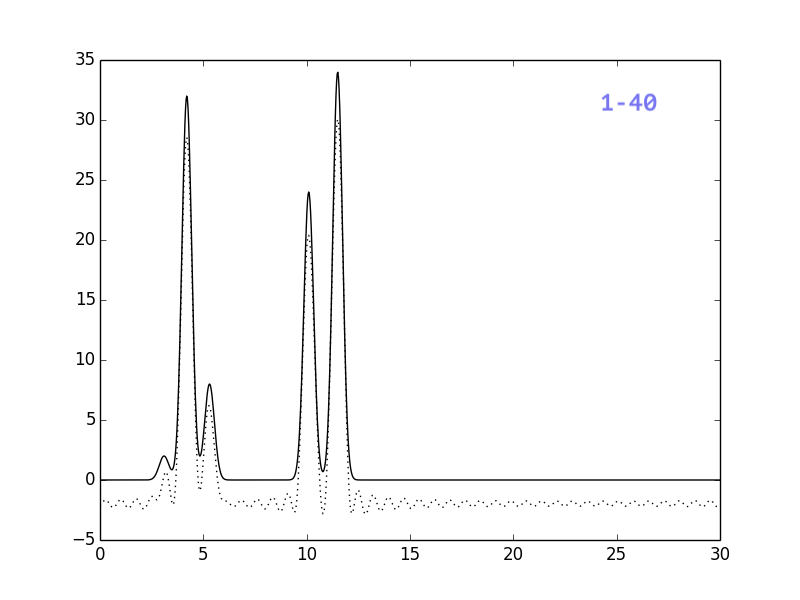
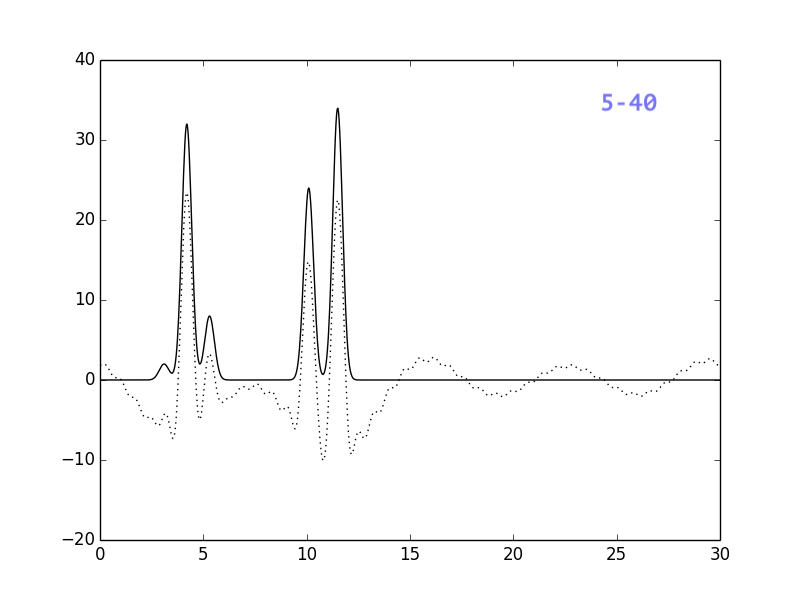
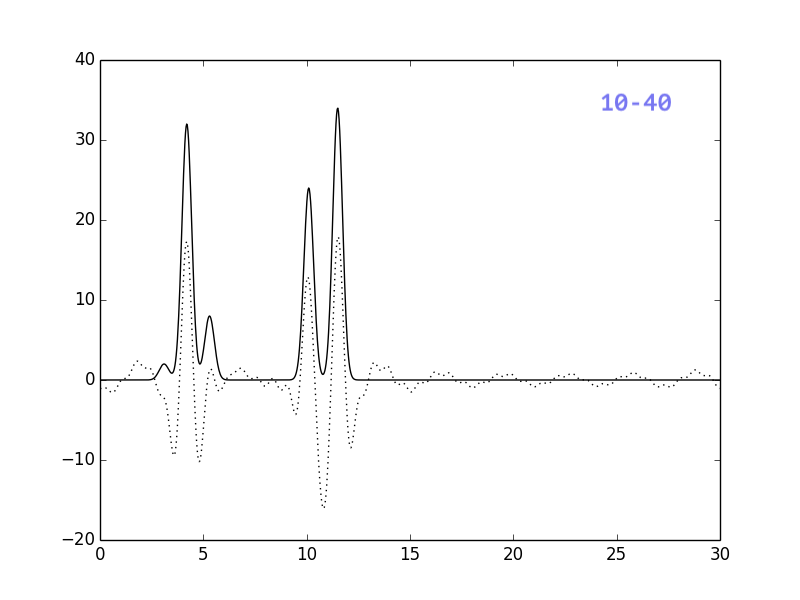
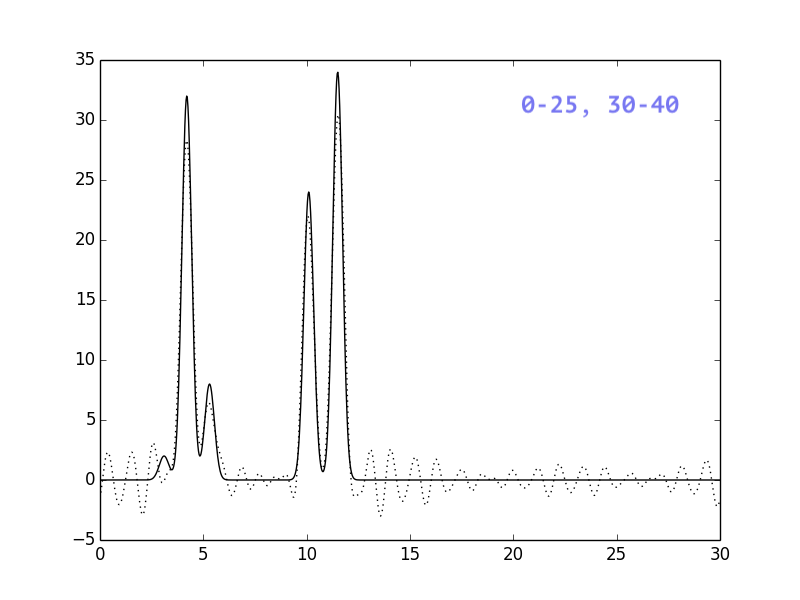
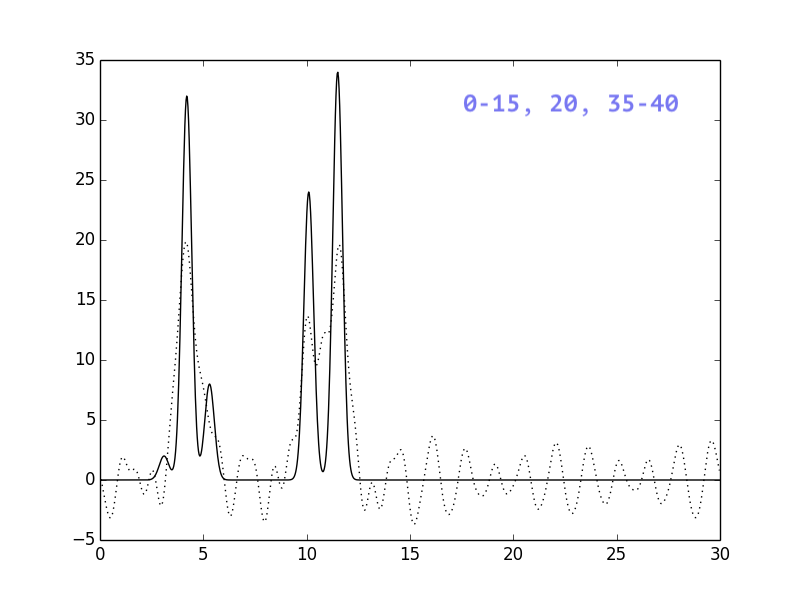
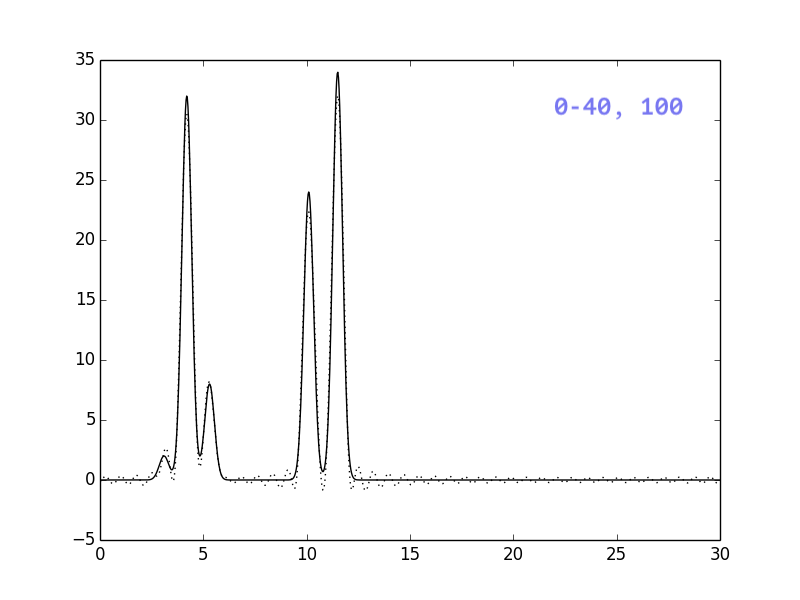
Если сравнить с картинками, полученными для ограниченного числа гармоник, можно сделать вывод, что отсутствие гармоник меньшего порядка более критично, чем отсутствие гармоник из середины или конца набора. Добавление 50-1 гармоники практически не повлияло на восстановление функции.

Итоговая таблица

Результаты по качеству восстановления функции ЭП из различных рассмотренных наборов гармоник приведены в таблице 1.

Для сравнения восстановленной функции с исходной использовались следующие "критерии качества":

  • Отличное восстановление — по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов");
  • Хорошее восстановление — можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума;
  • Среднее восстановление — положение каких-то атомов определить по восстановленной функции нельзя, других - можно;
  • Плохое восстановление — положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".

    • Полнота набора гармоник определяется как % гармоник (k штук) от полного числа гармоник (от 0 до n-й). Разрешение неполного набора я решила не определять.

    Таблица 1. Сводная характеристика восстановления функции ЭП из разных наборов гармоник
    Набор гармоник Разрешение, Å Полнота набора, % Шум (амплитуда), % Шум (фаза), % Качество восстановления
    Полный набор без шума
    0-5 6 100 0 0 Плохое
    0-10 3 100 0 0 Плохое
    0-15 2 100 0 0 Среднее
    0-20 1.5 100 0 0 Среднее
    0-25 1.2 100 0 0 Среднее
    0-30 1 100 0 0 Хорошее
    0-35 0.86 100 0 0 Отличное
    0-40 0.75 100 0 0 Отличное
    0-45 0.67 100 0 0 Отличное
    Полный набор c шумом
    0-40 0.75 100 10 0 Хорошее
    0-40 0.75 100 20 0 Хорошее
    0-40 0.75 100 30 0 Среднее
    0-40 0.75 100 0 10 Среднее
    0-40 0.75 100 0 20 Среднее
    0-40 0.75 100 0 30 Среднее
    0-40 0.75 100 10 10 Хорошее
    0-40 0.75 100 20 20 Среднее
    0-40 0.75 100 30 30 Среднее
    Неполный набор без шума
    1-40 - 97.6 0 0 Отличное
    5-40 - 87.8 0 0 Среднее
    10-40 - 75.6 0 0 Среднее
    0-25, 30-40 - 87.8 0 0 Среднее
    0-15, 20, 35-40 - 87.8 0 0 Плохое
    0-40, 50 - 100+ 0 0 Отличное
    В целом, почти высокие пики восстанавливались хорошо, так что качество в основном зависит от возможности восстановить мелкие пики. Из-за этого в некоторых случаях в общем неплохое восстановление оценивалось как "среднее".