Полезные ссылки
Молекулярная динамика биологических молекул в GROMACS.
Моделирование самосборки липидного бислоя из случайной стартовой конформации
-
Для работы будем использовать файлы:
дополнительной топологии для липида DPPC, dppc.itp;
параметры для липидов lipid.itp;
координаты одного липида dppc.gro;
файл-заготовка тополгии системы b.top;
файл параметров для минимизации энергии em.mdp;
файл параметров для "утряски" воды pr.mdp;
файл параметров для молекулярной динамики md.mdp.
-
На основе одного липида созадим ячейку с 64 липидами:
genconf -f dppc.gro -o b_64.gro -nbox 4 4 4
-
Установим в файле b.top правильное количество липидов в системе (64).
-
Сделаем небольшой отступ в ячейке от липидов, чтобы добавить примерно 2500 молекул воды:
editconf -f b_64.gro -o b_ec -d 0.5
-
Проведём оптимизацию геометрии системы:
grompp -f em -c b_ec -p b -o b_em -maxwarn 2 mdrun -deffnm b_em -v
Начальное значение максимальной силы равно 4.38e+05, конечное (после оптимизации) - 6.45e+02.
-
Добавим в ячейку молекулы воды типа spc:
genbox -cp b_em -p b -cs spc216 -o b_s
-
Проведем "утряску" воды:
grompp -f pr -c b_s -p b -o b_pr -maxwarn 1 mdrun -deffnm b_pr -v
-
Скопируем эти файлы на суперкомпьютер и запустим моделирование:
mpirun -np 16 -maxtime 1200 /home/golovin/progs/bin/mdrun_mpi -deffnm b_md -v
Номер моей задачи - 241064.
Анализ результатов
- Силовое поле, используемое при построении топологии, - ffgmx.
- Размер и форма ячейки: прямоугольный параллелепипед со сторонами 6.26000, 4.44300 и 5.77800 нм.
- Минимизация энергии:
- Алгоритм минимизации энергии:
integrator = l-bfgs
- Алгоритм расчёта электростатики:
coulombtype = Cut-off
- Алгоритм расчета Ван-дер-Ваальсовых взаимодействий:
vdw-type = Cut-off
- Алгоритм минимизации энергии:
- Модель, которой описывался растворитель: flexspc.
- Утряска растворителя:
- Число шагов: 10000.
- Длина шага: 0.001 пс.
- Алгоритм расчёта электростатики:
coulombtype = pme
- Алгоритм расчета Ван-дер-Ваальсовых взаимодействий:
vdw-type = Cut-off
- Алгоритм термостата:
Tcoupl = Berendsen
- Алгоритм баростата:
Pcoupl = no
- Основной расчёт МД:
- количество процессоров - 16.
- Длина траектории: 50 нс.
- Число шагов: 10000000.
- Длина шага: 0.005 пс.
- Алгоритм интегратора: md.
- Алгоритм расчёта электростатики:
coulombtype = pme
- Алгоритм расчета Ван-дер-Ваальсовых взаимодействий:
vdw-type = Cut-off
- Алгоритм термостата (контроль температуры "Velocity rescale"):
Tcoupl = v-rescale
- Алгоритм баростата:
Pcoupl = Berendsen
-
Начнем с визуального анализа движения молекул:
trjconv -f b_md.xtc -s b_md.tpr -o b_pbc_2.pdb -skip 20 -pbc mol
В результате получаем файл b_pbc_2.pdb. Как такового бислоя не образуется, однако образуется вытянутая мицелла примерно с 30 номера модели, что соответствует времени 15000 фемтосекунд.
-
Определим площадь, занимаемую одним липидом. Для этого получим размеры ячейки из траектории:
g_traj -f b_md.xtc -s b_md.tpr -ob box_1.xvg
В файле box_1.xvg содержатся размеры ячейки. В первой колонке приводится время, а в следующих трёх - размер ячейки (длины по каждым из осей). Зависимость площади (нормированной на один липид в слое) в квадратных нанометрах по соответствующим осям (вычисленной как произведение длин по осям, не являющимися нормалью к поверхности бислоя, (то есть по осям Y и Z) деленным на 32 (общее число молекул липида в одном слое)) представлена на графике: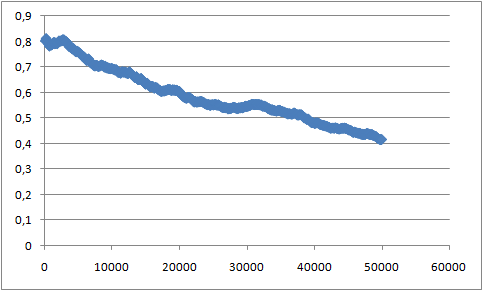
Зависимость была построена в Excel. По вертикальной оси площадь 1 молекулы липида, кв. нм. По горизонтальной - время, фс.
Как можно видеть, площадь приходящаяся на 1 молекулу липида непрерывно уменьшается во время образования бислоя.
-
Определим изменение гидрофобной и гидрофильной поверхностей в ходе самосборки:
g_sas -f b_md.xtc -s b_md.tpr -o sas_b.xvg
В результате получаем файл sas_b.xvg с данными о гидрофильной и гидрофобной поверхностях в каждый момент времени. Зависимость изменения гидрофобной (синяя) и гидрофильной (красная) поверхностей от времени: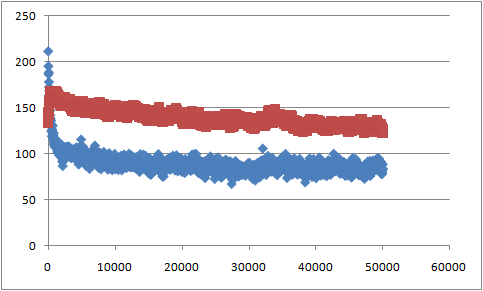
Таким образом, при образовании бислоя происходит уменьшение как гидрофобной, так и гидрофильной поверхностей, что приводит к уменьшению энергии системы в водном растворе (что и является движущей силой образования бислоя).
-
Традиционной мерой оценки фазового состояния бифильных молекул является мера порядка.
Для анализа был получен индексный файл sn1.ndx.
Для конца траектории:g_order -s b_md -f b_md.xtc -o ord_end.xvg -n sn1.ndx -b 45000 -d X
Для начала траектории:g_order -s b_md -f b_md.xtc -o ord_start.xvg -n sn1.ndx -e 5000 -d X
График с изображением меры порядка для разных атомов липида для начала траектории представлен ниже: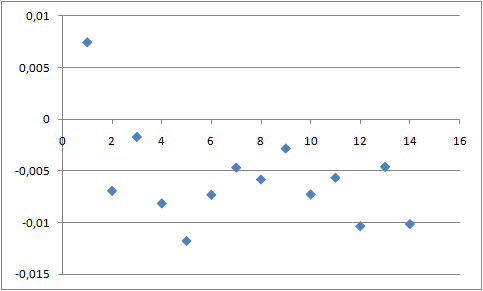
Такой же график для конца траектории: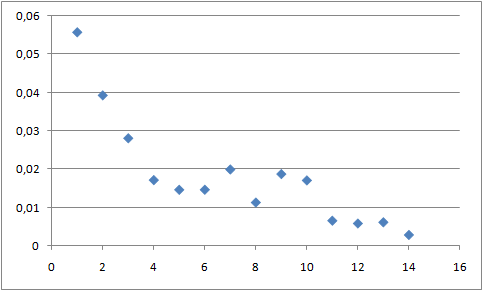
В начале траектории значения меры порядка сильно колебаются, что связано с хаотичностью движений молекул липидов. В конце траектории видно, что головки липидов более ограничены в движении, чем хвосты.
В конце траектории, когда мицелла приобрела четко сформированную структуру, подвижность молекул липидов падает, по сравнению с началом траектории, когда структуры еще не образовано.