Занятие 3. Филогенетические деревья
Оценка достоверности реконструированной топологии с помощью бутстреп-анализа
Был проведен бутстреп-анализ выравнивания мутированных последовательностей, соответствующих листьям исходного дерева.
Этапы работы:
fseqboot ali.fasta -auto # создает 100 бутстреп-реплик выравнивания
fdnaml ali.fseqboot -auto # создает ali.treefile, в котором 100 скобочных формул, соответствующих реконструкциям, сделанным по каждому из выравниваний
fconsense ali.treefile -auto # создает файл, в который будут помещены результаты бутстреп-анализа.
Здесь лежит выходной файл в текстовом формате. А здесь лежит множественное выравнивание всех листьев исходного дерева.
Полученное консенсусное дерево по топологии совпадает с исходным:
+---------------------------C | | +-------------F | +100.0-| | | | +------E | | +-92.0-| +------| +------D | | +------A +--------96.0-| +------BВ этом можно также убедиться с помощью таблиц разбиений по листьям:
Исходное:A B C D E F . . * * * * . . . * * * . . . * * .
Консенсусное:C F D E B A . * * * . . . . . . * * . . * * . .
Процент достоверности ветвей 100, 92 и 96. Это значительно превышает порог достоверност в 70 процентов, что дает право утверждать - дерево правильное.
Бутстреп-анализ хорошо справился с задачей оценки достоверности филогенетического дерева.
Изображение филогенетического дерева в графическом формате
С помощью программы fdrawtree было нарисовано исходное дерево (((А:90,B:90):5,C:70):30,((D:90,E:90):4,F:80):20);
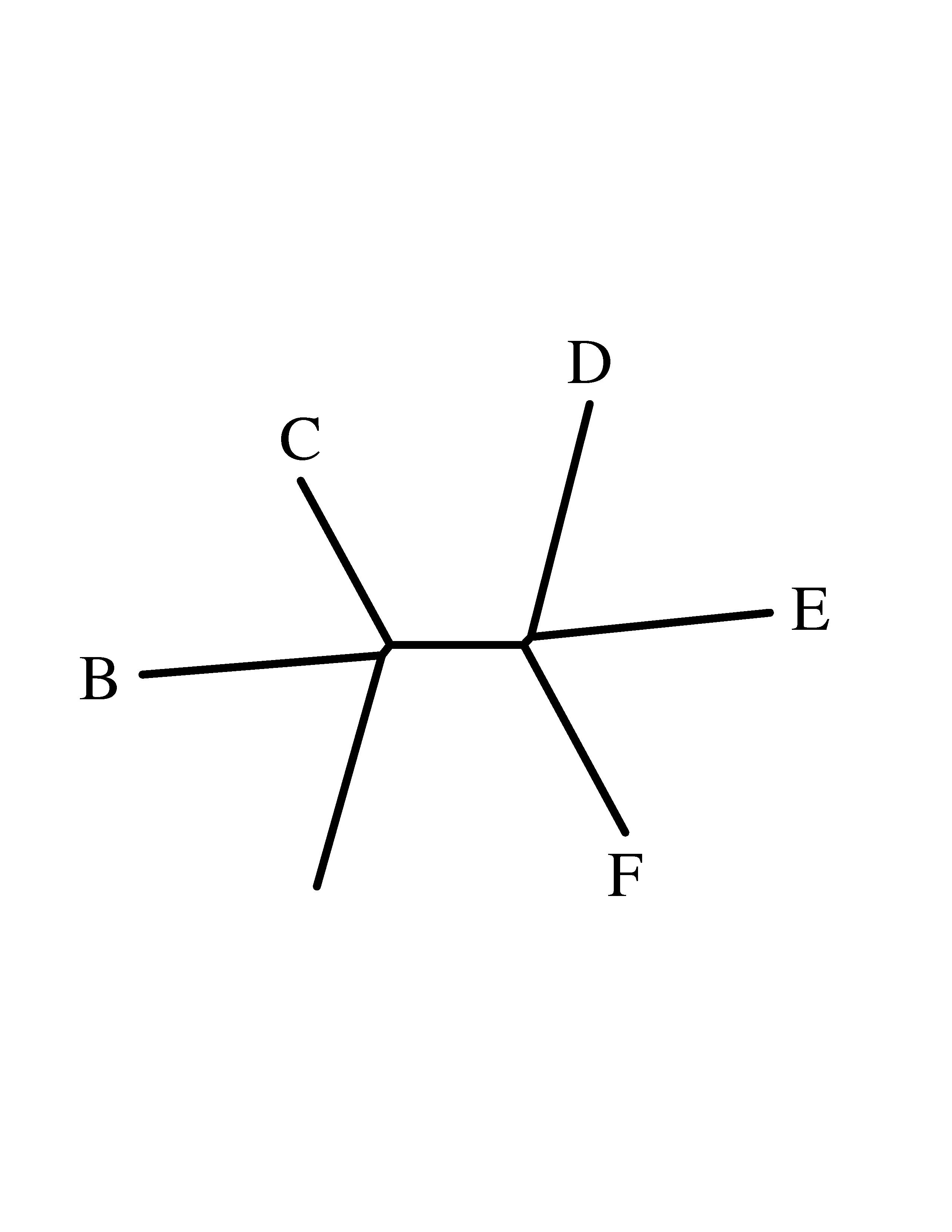
Построенное дерево безкорневое, но длина каждой ветки точно рассчитана исходя из скобочной формулы. Не понятно, куда пропал потомок А, скорей всего он скрывается под неподписанной ветвью.
вернуться к 3 семестру