Сравнение параметров выравнивания пары гомологичных белков.

Параметры, используемые программами по умолчанию.

Программа	Тип выравнивания	Матрица весов	Штраф за гэпы	Штраф за концевой гэп
needle	глобальное	EBLOSUM62	10.0	10.0
water	локальное	EBLOSUM62	10.0	10.0

Для того, чтобы программы пакета EMBOSS выдавали результат в формате fasta в пригодном для jalview виде, необходимо модифицировать вывод этих программ, прописав при вызове дополнительные атрибуты -aformat3 fasta -aextension fasta. Таким образом получится файл, в котором последовательности представлены в fasta-формате.

К сожалению, выравнивание с параметрами по умолчанию совпадало у двух программ. Поэтому окончательный отчет строится на основе данных, полученных при увеличенном в два раза значении шрафа за открытие гэпа.

Сравнение локального выравнивания двух гомологичных белков с глобальным.

Тип парного выравнивания	Длина выравнивания	% консервативных остатков	% функционально консервативных остатков	% гэпов	число инделей
глобальное	663	45.1	61.7	11.8	9
локальное	607	52.8	70.7	2.9	5

Локальное выравнивание можно посмотреть по этой ссылке, a глобальное по этой. Здесь и далее раскраска по схеме Blosum62 c порогом консервативности 70%. Основные различия заключаются в том, что глобальному выравниванию приходится работать со всем объемом белка и за счет этого цифры в таблице занижены для глобального выравнивания через посредство несбалансированных краев последовательностей.

Локальное выравнивание негомологичных последовательностей.

Идентификаторы	Длина выравнивания	% консервативных остатков	% функционально консервативных остатков	% гэпов	число инделей
E8YFS1_9BURK A0A0U3M8E6_9BURK	122	23	35.2	32.8	5
E8YFS1_9BURK A0A0U3QKR4_9MICC	93	26.9	32.3	28.0	3
E8YFS1_9BURK A8FC81_BACP2	360	21.4	34.7	32.2	21
E8YFS1_9BURK D1C2A4_SPHTD	221	24.9	31.7	26.2	12
E8YFS1_9BURK Q82P56_STRAW	270	19.3	31.9	40.0	15

Пример выравнивания негомологичных белков. По наблюдаемым данным, выравнивания негомологичных белков короче, содержат меньший процент консервативных и функционально консервативных позиций, а также гораздо более насыщенны инделями.

Сравнение трех выравниваний

Подправленные выравнивания доступны здесь. Отличия глобального и локального выравнивания от выравнивания, являющегося частью множественного сильнее, чем их отличия друг от друга. Первое различие состоит в том, что изолейцин 80 второй последовательности гомологичен валину 83 первой(в множественном выравнивании), тогда как в двух других выравниваниях он гомологичен аланину 85. Второе различие состоит в том, что лизин 507 первой последовательности множественное выравнивание ставит в соответствие серину 500 второй, а парные выравнивания ставят напротив аланин 495. Третье различие заметно при анализе С-концов выравнивания. В локальном выравнивании "хвост" отсутствует, а в глобальном его характер различается с множественным за счет вариативного расположения гэпов. Множественное выравнивание справляется с задачей объективно хуже, поскольку учитывание других последовательностей отрицательно влияет на сравнение конкретных двух. Из двух парных выравниваний глобальное более отражает биологическую суть, пскольку оно не игнорирует участки возможной гомологичности на концах выравнивания.

Ориентированный граф для построения оптимального глобального выравнивания с аффинными штрафами за индели

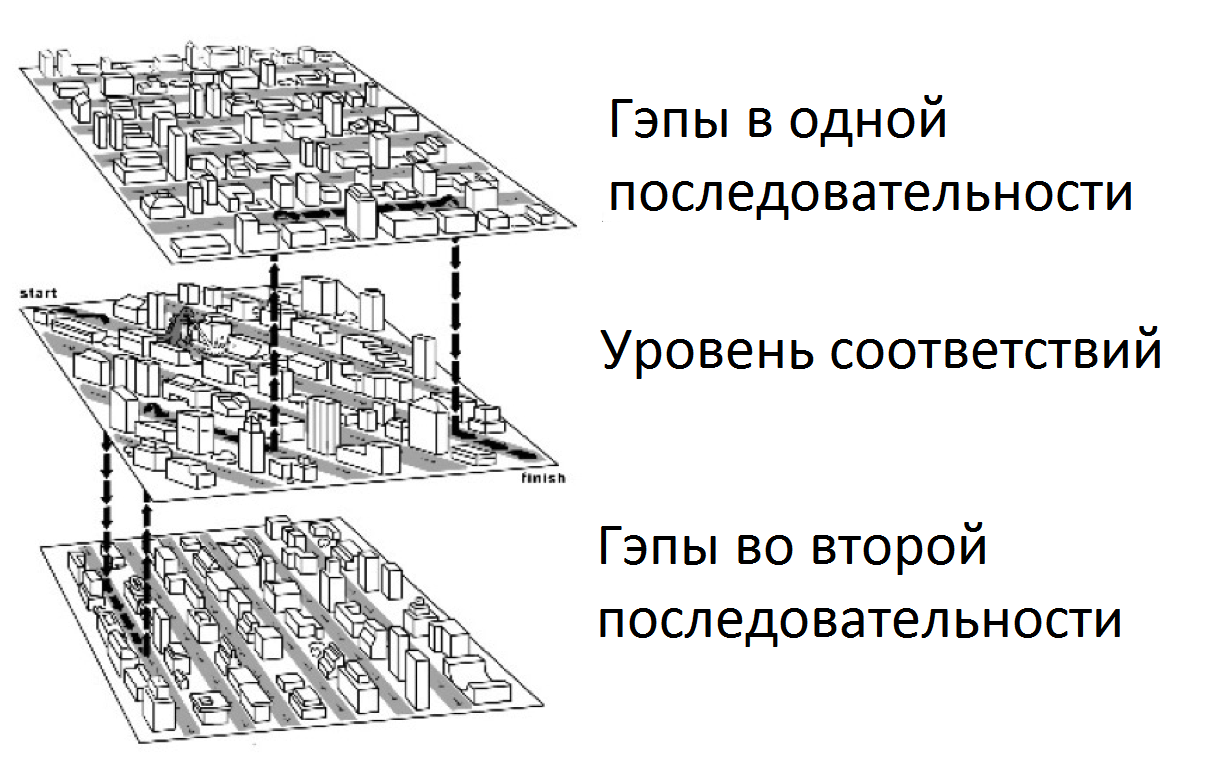
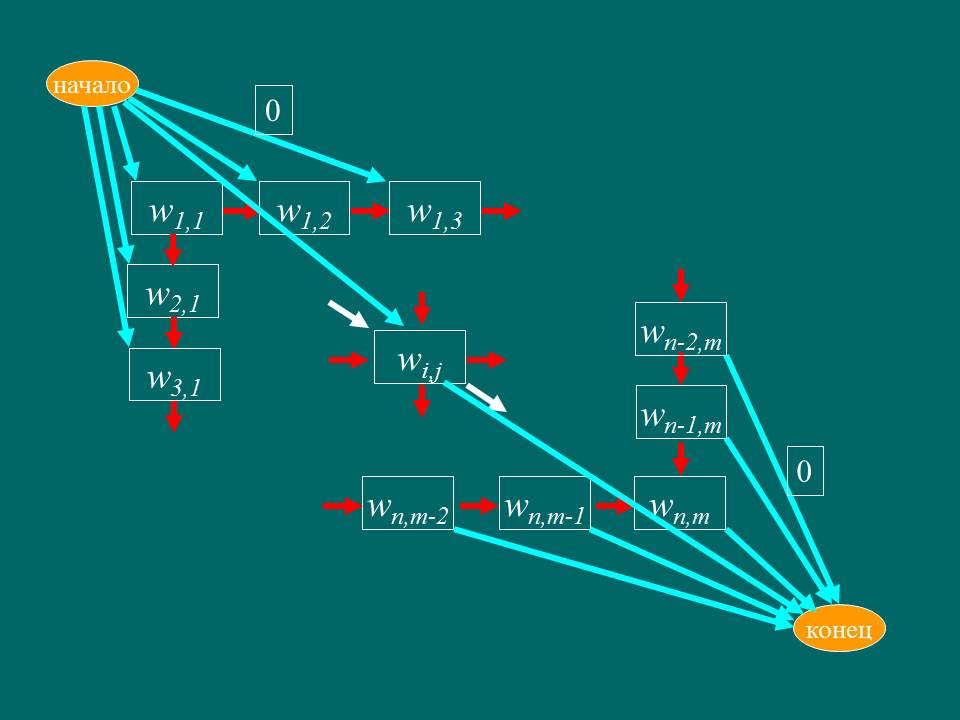
Этот граф оптимально представлять в виде изоморфного ему графа, похожего на трехслойный пирог. Мы начинаем и заканчиваем на среднем уровне. Верхняя таблица создает/расширяет гэпы в верхней последовательности, нижняя делает то же самое в левой, а средняя работает только с совпадениями/разночтениями. Итак, из каждой вершины среднего уровня есть три пути. Можно пойти по диагонали серединного слоя, заплатив штраф за различие либо получив бонус за совпадение. Можно подняться или опуститься на уровень, заплатив штраф за открытие гэпа. На крайнем уровне из каждой вершины есть два пути: продолжить гэп, заплатив штраф за его продолжение, или закрыть гэп, вернувшись на средний уровень совершенно бесплатно. Оптимальным является маршрут с максимальным количеством очков.

Ориентированный граф для построения оптимального локального выравнивания с линейными штрафами за гэпы

В данном графе в каждую вершину приходит ребро нулевого веса из начала, а выходит ребро нулевого веса в конец(голубые стрелки). Кроме этого, из каждой вершины выходят ребра вниз и вправо, которые отражают возможность вставки гэпа в левую либо верхнюю последовательность и имеют вес штрафа за гэп(красные стрелки). Самые важные стрелки - белые. Переход по ним нужен при сопоставлении символов двух последовательностей. Вес этого ребра заисит от выбранной матрицы сопоставлений.

Матрица "весов дружелюбности"

Матрица составлялась на основе случайной выборки(театр) цепочек друзей (ряды зрительного зала), начинающихся с подписчиков на один из самых популярных пабликов ВКонтакте – «Киномания». Алгоритм составления цепочек следующий:

1. С помощью биологического генератора случайных чисел выбирался один из подписчиков указанного паблика.
2. Из его друзей аналогично выбирался пользователь и проверялось, является ли он подписчиком паблика «Киномания». В случае, если он являлся подписчиком, ему присваивалась «1», если нет – «0»
3. Действие 2. повторялось до длины цепочки в 10 человек.(следующий человек выбирался из друзей предыдущего)
4. Алгоритм был распространен на 10 подписчиков паблика.