


В данной работе исследовалось качество восстановления одномерной функции ЭП в зависимости от количества гармоник ряда Фурье, использованных для ее построения, а также от наличия шума в моделируемом эксперименте.
Задание функции ЭП для модели
Была создана модель компьютерного эксперимента: 2 линейных трехатомных молекулы O-C-N и Cl-Ca-Cl. Для этой модели была задана функция на интервале [0Å, 30Å], описывающая ЭП с помощью скрипта compile-func.py:
python compile-func.py -g 32,3,8+24,3,9.5+28,3,11+71,2.00,16+80,2.0,17.5+71,2.00,19
Функция имеет вид нескольких гауссовых кривых с центром в разных точках.
gauss = lambda*exp(-(beta²)*(X-gamma)²)
lambda - высота гауссовской кривой, соответствующая максимуму электронной плотности в центре атома. Пропорционально числу электронов в атоме:
beta - ширина колокола, которая примерно соответствует диаметру атома. Для простоты были приняты значения только 1 и 2
gamma - координата максимума гауссовой кривой. Расстояние между молекулами - 5.5 Å, длина всех связей - 1.5 Å.
График электронной плотности модели атомов представлен на рисунке 1. Выходной файл скрипта доступен по ссылке.
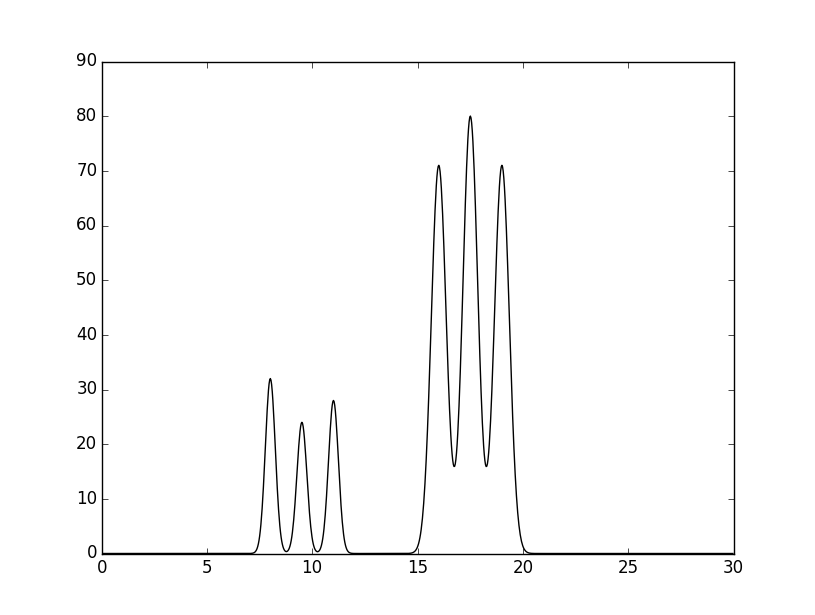
Рис. 1. График электронной плотности модели атомов
Коэффициенты Фурье рассчитываются с помощью скрипта func2fourier.py следующей командой:
python func2fourier.py -i func.txt
Выходной файл скрипта – файл func_ft.txt.
Отбор гармоник
Набор гармоник ряда Фурье называется полным, если известны все гармоники с номерами 0, 1, 2, ..., n. Разрешением полного набора гармоник называется период гармоники с номером n, то есть с наибольшим номером. Период гармоники равен расстоянию между соседними максимумами синусоиды. Его также называют длиной волны этой гармоники.
По полному набору гармоник был построен график восстановленной функции электронной плотности модели с помощью скрипта fourier2func.py командой:
python fourier2func.py -f func.txt -i func_ft.txt -s -o harm_full.txt
Графики первоначальной и восстановленной функции представлены на рис.2. Из рис. 2 видно, что при количестве гармоник, равном 499 (в файле func_ft.txt именно такое количество гармоник - от 0 до 498), удается восстановить исходную функцию без каких-либо потерь информации. То есть восстановление отличное.

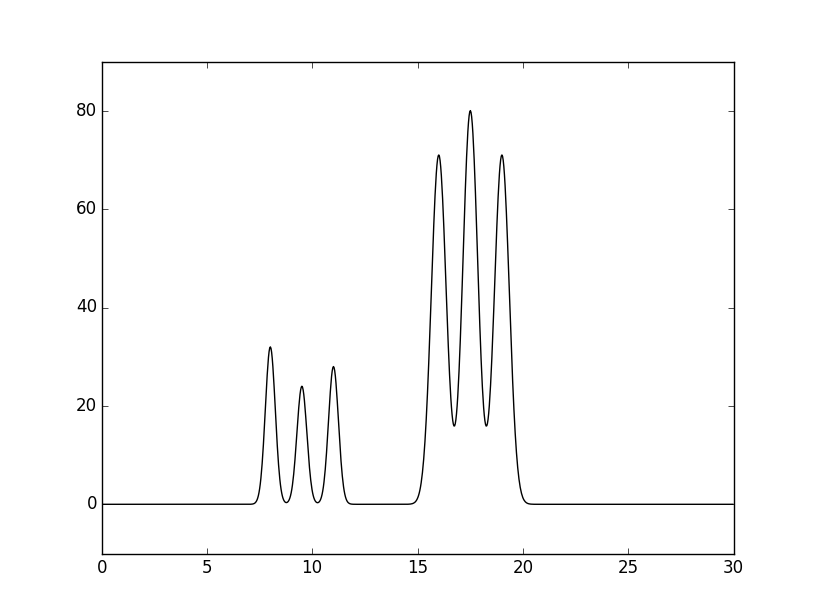
Рис. 2 Графики первоначальной (слева) и восстановленной функции (справа)
Как сравнить восстановленную функцию с исходной?
Восстановим теперь функцию по меньшему полному набору гармоник. На рис. 3 (а-г) представлены графики функций, восстановленных по неполному набору гармоник, а именно 5, 10, 20, 40. Изображения были получены с помощью:
python fourier-filter.py -r 0-n -i func_ft.txt -o hf_n.txt
python fourier2func.py -f func.txt -i hf_n.txt -o hf_n_f2f.txt
где n - наибольший номер гармоники
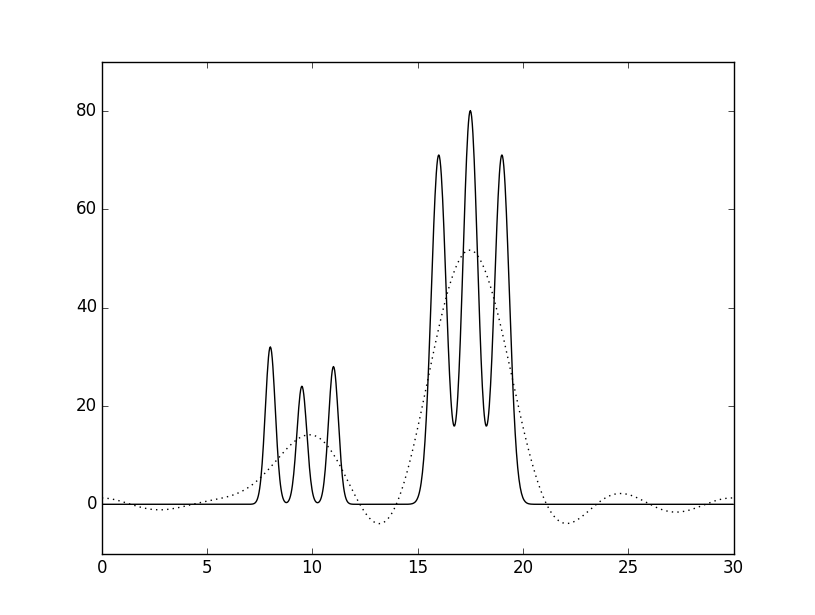
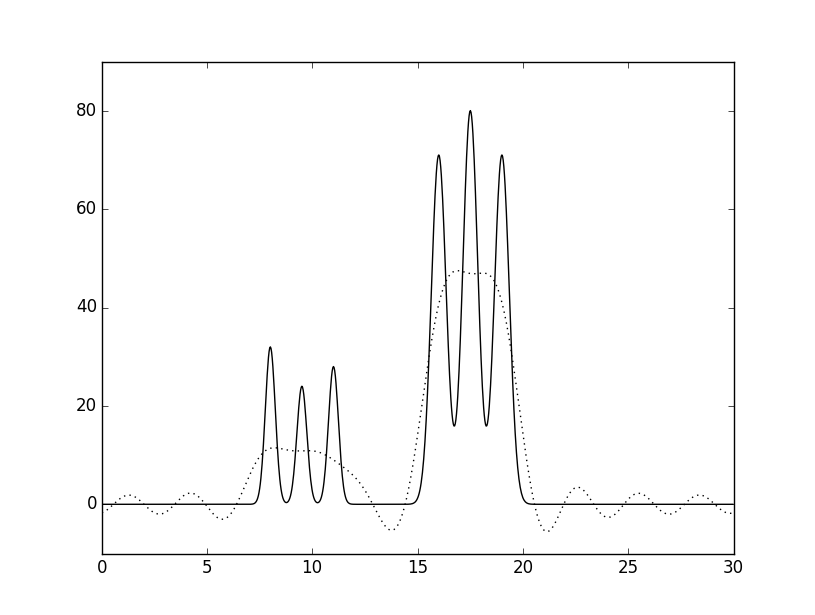
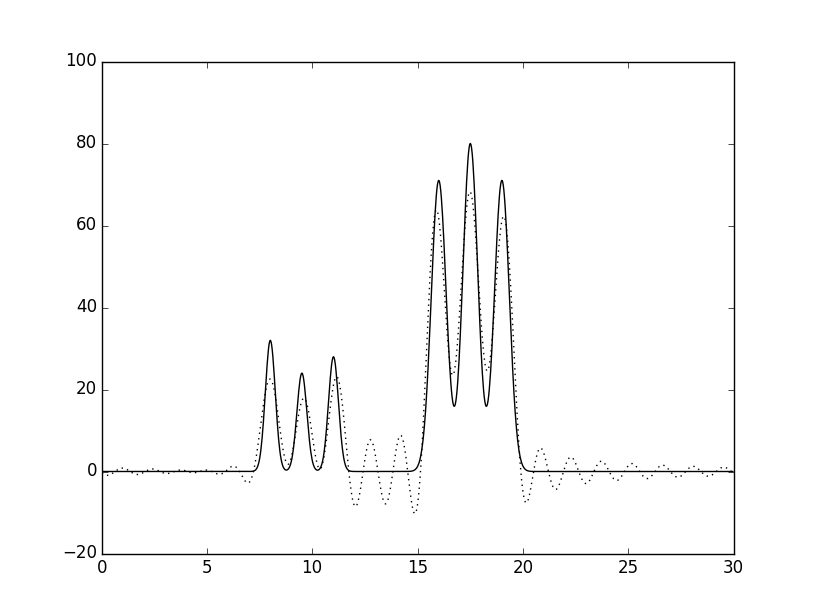
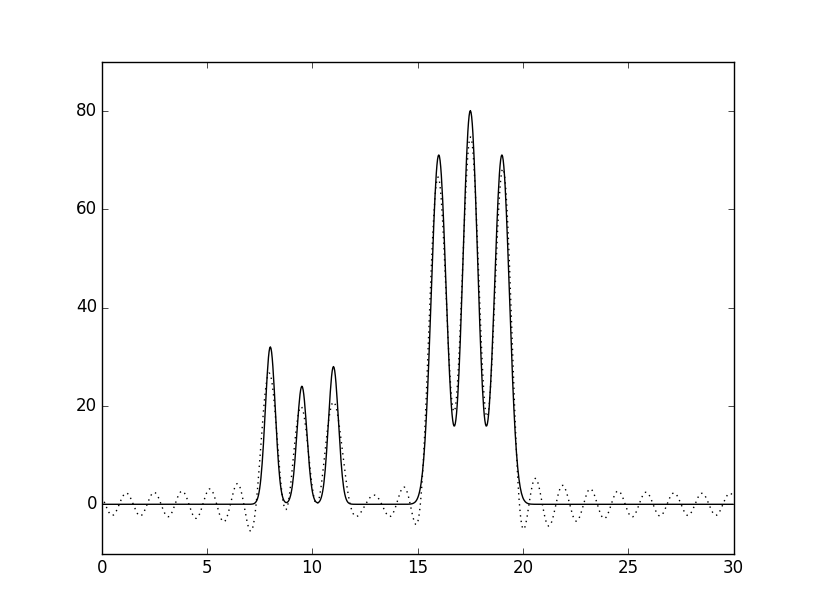
Рис.3 Графики восстановленных функций
Графики исходной функции представлен сплошной линией, а восстановленных функций - пунктиром. Номера гармоник: A. - 0-5; Б. - 0-10; В. - 0-20; Г. - 0-22.
Исходя из графиков на рис.3, видно, что гармоник 22 - это минимальное число гармоникпри котором функция сохраняет отличное восстановление.
Добавим шум к амплитудам и фазам при восстановлении по полному набору гармоник. Стоит отметить, что шум в фазах вносит гораздо больший вклад в изменения, чем шум в амплитудах.
Добавление шума к амплитуде (F) и к фазе (P)
python func2fourier.py -F 10 -P 0 -i func.txt -o noise_f10p0.txt
python fourier-filter.py -r 0-22 -i noise_f10p0.txt -o noise_f10p0_22.txt
python fourier2func.py -i noise_f10p0_22.txt -o func_noise_f10p0_22.txt
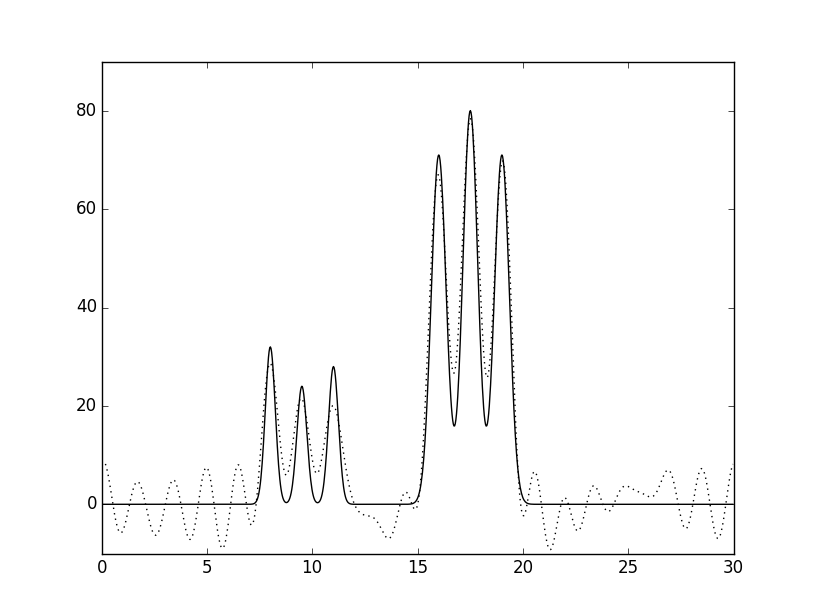
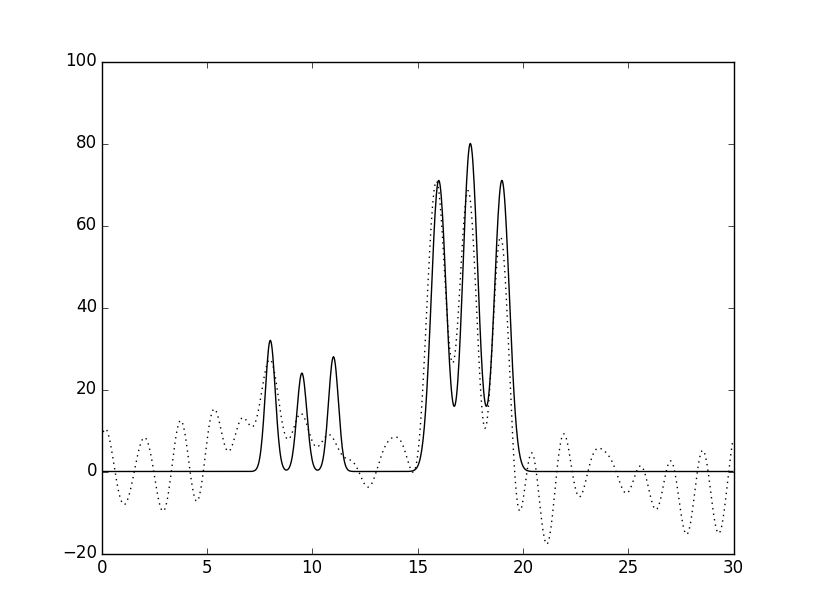
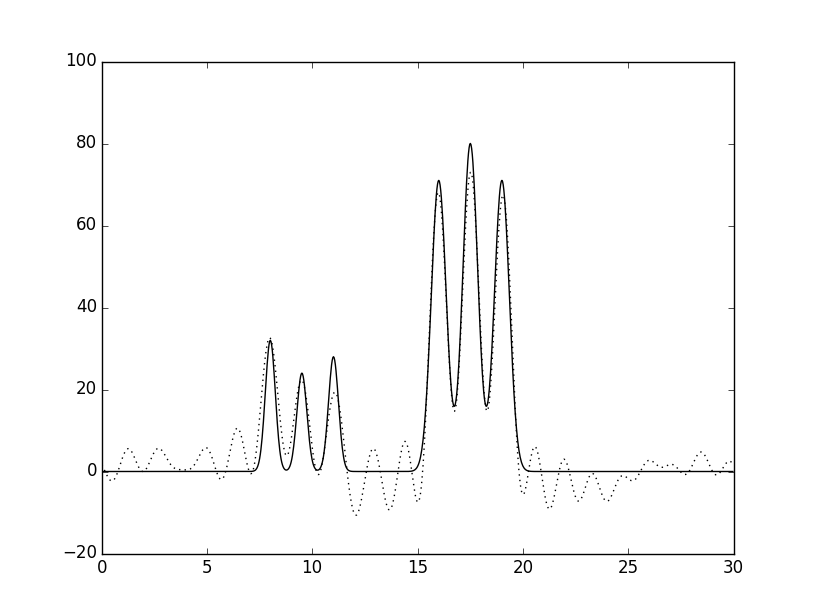
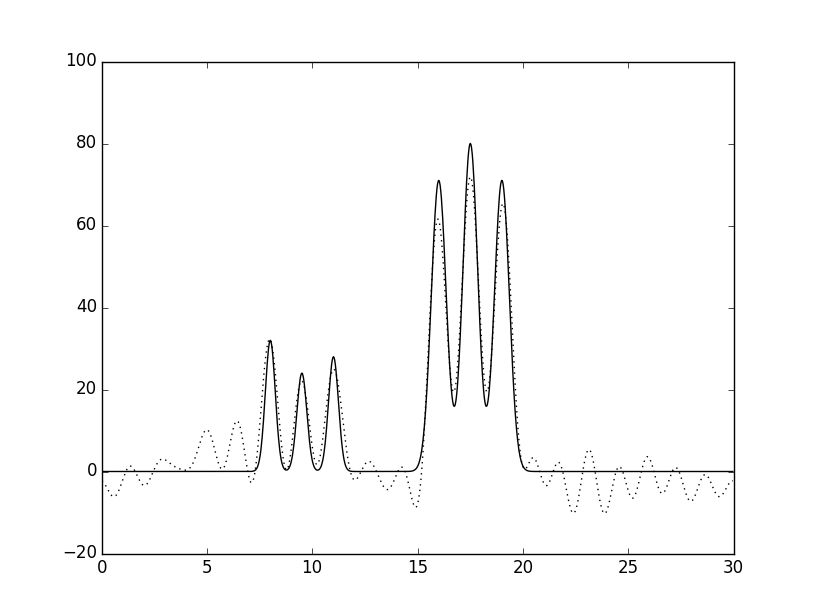
Рис.4 Графики восстановленных функций
Графики изначальной функции электронной плотности (слошная линия) и восстановленной (пунктирная линия) для 22 гармоник A. - с шумом 25% к амплитуде; Б. - 25% к фазе; В - 15% к амплитуде и 5% к фазе. Г - 5% к амплитуде и 15% к фазе
Неполные наборы гармоник
Сделаем неполные наборы гармоник для набора n0: удалим несколько первых гармоник, удалим 9% серединных гармоники, добавим гармонику с номером n0+10 (32).
Первую гармонику я удалять не стала, так как очевидно график никак не ухудшится, а только сдвинется на константу по оси y, так как эта гармоника есть константа, длины волны у нее нет. Если же удалить первые три, то вычитается синусоида с периодом T/3.
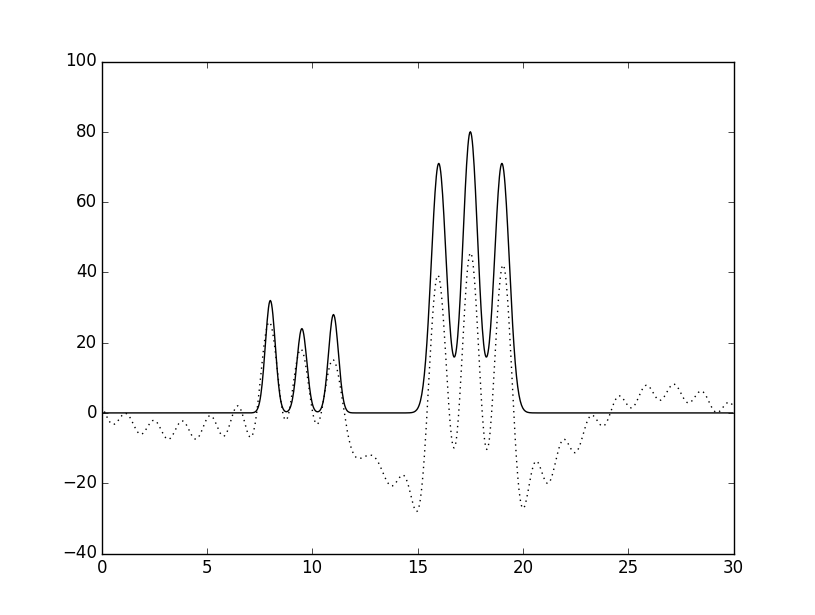
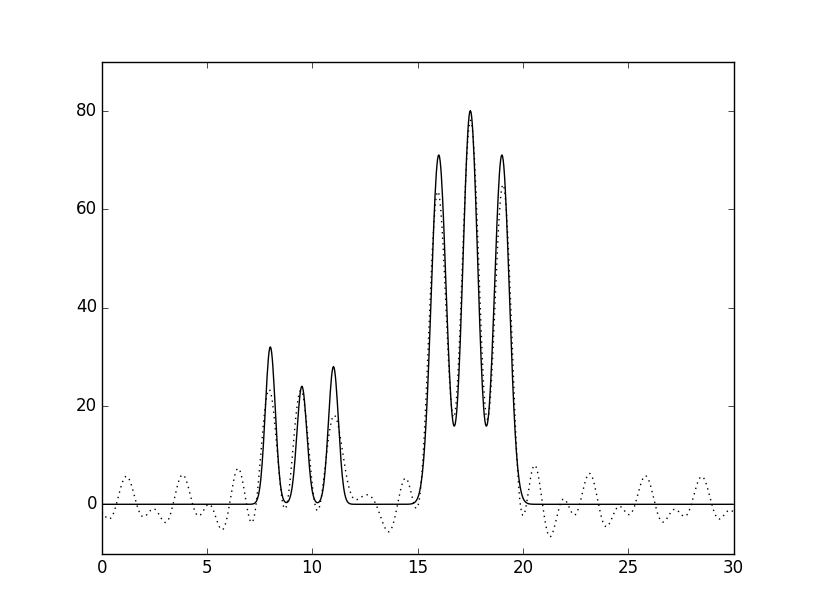
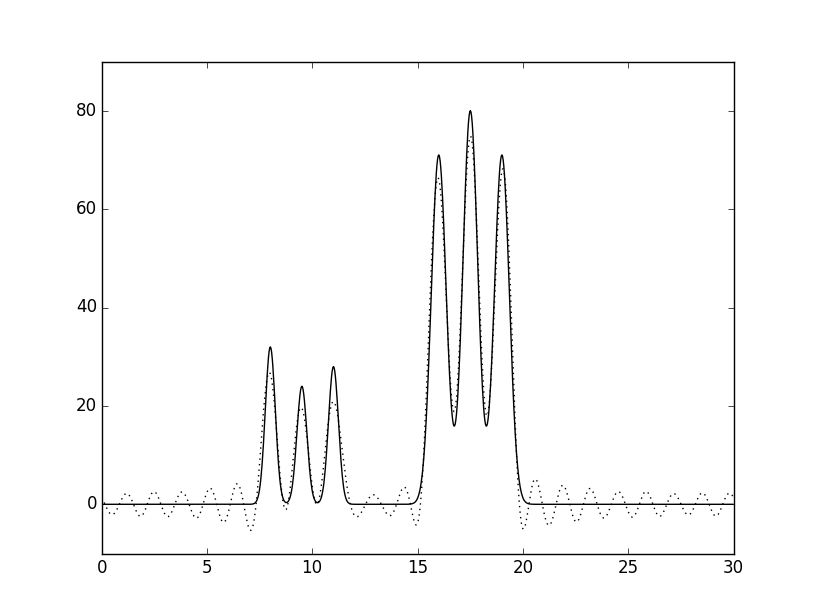
Рис.5 Неполные наборы гармоник
Графики функций, восстановленных по неполному набору гармоник изображены пунктиром, исходная функция - сплошной линией; А - Удаление первых трех гармоник; Б - Удаление 9% гармоник из середины набора; В - Добавление гармоники с номером n0+10.
Удаление первых трех гармоник почти не повлияло на общую картину, что немаловажно для РСА, так как они могут потеряться. Вследствие удаления 10% гармоник в середине набора качество восстановления сильно ухудшилось, максимумы от атомов стали почти не отличимы от шума. Добавление гармоники с номером 32 никак не изменило график, т.к. высокочастотные гармоники имеют низкую амплитуду и не могут сильно изменить график.
Итоги
Для полного набора гармоник разрешение - это период гармоники с наибольшим порядковым номером. В нашем случае, если в наборе 499 гармоник, то разрешение будет d=T/n: 30 / 499 = 0,06.
Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо учитывать полноту данных (процент гармоник с длиной волны большей d от полного набора гармоник с количеством гармоник, равным наибольшей гармонике в данном неполном наборе). Для сравнения структур можно выбрать порог по полноте данных. Тогда значения разрешения будет равно d из предыдущего параграфа, но не меньше d'=T/n', где n' - наибольшая гармоника рассматриваемого набора, при условии, что берутся в расчет не меньше первых k% гармоник (k% - порог на полноту данных).
|
Набор гармоник |
Разрешение (Å) |
Полнота данных (%) |
Шум амплитуды (% от F) |
Шум фазы (% от phi) |
Качество восстановления |
|
Полный набор гармоник |
|||||
|
0-498 |
0.06 |
100 |
0 |
0 |
отличное |
|
0-5 |
6 |
100 |
0 |
0 |
плохое |
|
0-10 |
3 |
100 |
0 |
0 |
среднее |
| 0-20 |
1.5 |
100 |
0 |
0 |
хорошее |
|
0-22 |
1.36 |
100 |
0 |
0 |
отличное |
|
0-22 |
1.36 |
100 |
25 |
0 |
хорошее |
|
0-22 |
1.36 |
100 |
0 |
25 |
среднее |
|
0-22 |
1.36 |
100 |
15 |
5 |
хорошее |
|
0-22 |
1.36 |
100 |
5 |
15 |
хорошее |
|
Неполный набор гармоник |
|||||
|
3-22 |
1.36 |
0.86 |
0 |
0 |
отличное |
|
0-10, 12-22 |
1.36 |
0.91 |
0 |
0 |
хорошее |
|
0-22, 32 |
1.36(0.94) |
100(0.69) |
0 |
0 |
отличное |