Алгоритмы реконструкции деревьев

Вспомним как выглядит правильное дерево.

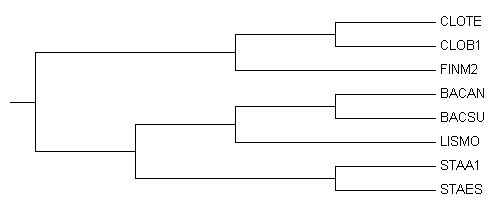Рис. 1. Структура таксономически правильного дерева.

1. Укоренение в среднюю точку

Укореним в среднюю точку дерево, полученное программой Mega из JalView с помощью алгоритма neighbor-joining. Для этого воспользуемся программой retree пакета PHYLIP и программой MEGA (для визуализации изображения). Получаем:

Исходное дерево	Полученное дерево

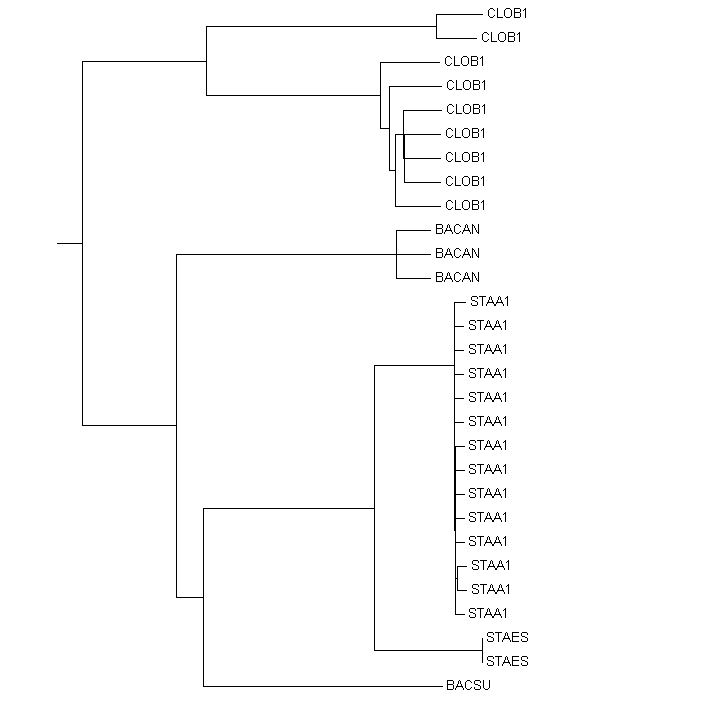Ветвь, в которую произошло укоренение показана на рисунке выше стрелочкой. Полученное укоренинием в среднюю точку дерево можно считать более правильным по сравнению с исходным (см. STAES и STAA1), хотя в нем по-прежнему неверны взаимоотношения между BACSU и BACAN.

2. Использование внешней группы

Методом максимальной экономии ("Maximum parsimony") не реконструируют длины ветвей, поэтому деревья, постоенные с его помощью невозможно укоренить в среднюю точку. Однако можно воспользоваться укоренением с помощью внешней группы. Будем использовать в качестве внешней группы белок того же семейства из кишечной палочки Escherichia coli ((if2_ecoli).

Для этого добавим к последовательностям последовательность белка if2_ecoli, выровнем их вместе (в JalView: Web Service > Alignment > Muscle with Defaults) и импортируем в MEGA. В программе MEGA выберем в меню Subtree раздел Root и указываем ветвь, ведущую к ECOLI. А чтобы получить изображение укоренённого дерева без ECOLI, нужно воспользовавться кнопкой "Show Subtree Separately" (изображение голубой лупы на фоне дерева на левой панели окна MEGA).

Исходное дерево (до укоренения)	Полученное дерево

В полученном дереве укоренние произошло в ветвь {((CLOB1,CLOTE),FINM2), все остальные}. Это укоренение можно считать верным, т.к. оно совпадает с изображением таксономического дерева.

3. Бутстрэп

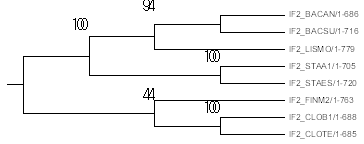
Бутстрэп-анализ можно проводить различными методами. Для этого в окошке, которое открывается после вызова программы MEGA, в меню "Test of Phylogeny" выбераем "Bootstrap method" и указываем число реплик = 100. Программа выдала два дерева - "Original tree" и "Bootstrap consensus tree", которые одинаковые (рис. 2) и они не отличаются от правильного дерева (рис. 1). Так же можно заметить, что хотя ветвь ((CLOB1,CLOTE),FINM2) и имеет не большое подтверждение, она является правильной.

Рис. 2. Структура деревьев (Original tree и Bootstrap consensus tree), полученных в программе MEGA по алгоритму Бутстрэп анализа.

Источники информации:

Сервер kodomo ФББ МГУ им. Ломоносова