В качестве последовательностей для сравнения я взяла последовательности из выравнивания seed для семейства доменов PF00004. В нем находится 207 последовательностей. Выравнивание производилось 3мя программами - MAFFT, T-COFFEE и MUSCLE. Для сравнения выравниваний я использовала программу, написанную Никой Братц.
СкриптПри сравнении выравниваний сделанных MAFFT и T-COFFEE одинаково выровнялись 3 блока:(10,22)=(8,20);(49,50)=(42,43);(147,148)=(162,163). Одиннаковых колонок не вошедших в блоки нет.
Для MAFFT и MUSCLE совпал всего 1 блок (колонки указаны соответственно): (10,22)=(8,19). Одиннаковых колонок, не вошедших в блоки так же нет.
Такое маленькое совпадение скорее всего связано с большим количеством последовательностей. Поскольку все использованные алгоритмы MSA эвристические и не находят оптимального решения, при увеличении числа последовательностей во входе разница между выдачами разных алгоритмов увеличвается
Проект jvpСравнение выравниваний, сделанных разными программами
Для сравнения я выбрала белки из того же семейства PF00004 c pdb_id: 1D2N, 1DO0, 1IQP. Сравнивала выравнивание, полученное MAFFT с "сведенным" к одному выравниванием по совмещению структур (Рис. 1) той же самой программой. Было найдено 16 блоков (для удобства доступны по файлу ниже, колонки указаны соответственно). колонки не вошедшие в блоки: 97=91; 237=232; 354=448; 393=347; 461=418
У выравниваний совпал 23 и 21 процент колонок, что гораздо выше, чем в прошлом пункте (от 3 до 5 процентов для всех выравниваний). Однако этот процент все еще кажется мне маленьким. Связано это скорее всего с тем, что функции (а следовательно и структуры) выбранных белков сильно различаются (1D2N - N-этилмалеимид-чувствительный белок слияния, функция - участие в слиянии мембран; 1DO0 - шаперон; 1IQP - загрузчик скрепки), что сильно ухудшает качество выравнивания таким способом. Так же на результат мог повлиять способ объединения pairwise выравниваний.
Проект jvp совпавшие колонки 3D vs MAFFT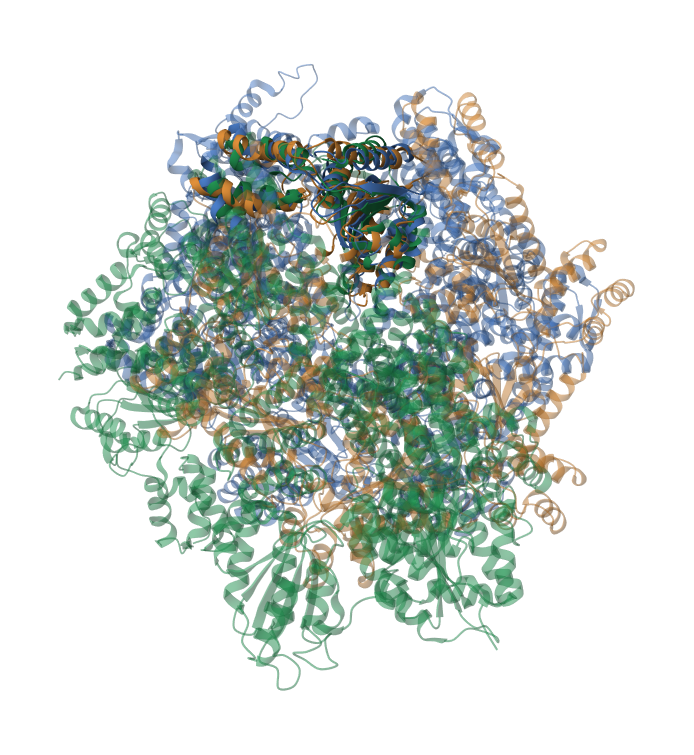
Описание работы программы MAFFT
Алгоритм MAFFT — эвристический метод для нахождения множественного выравнивания, применяющий быстрое преобразование Фурье. Его выполнение включает последовательность этапов. Изначально алгоритм вычисляет парные выравнивания для всех последовательностей, что позволяет построить матрицу дистанций. Эта матрица, рассчитываемая с учётом весов выравниваний, нужна для оценки их различий. Следующим шагом является построение направляющего дерева. Используя прогрессивное выравнивание и двигаясь от листьев к корню, алгоритм объединяет выравнивания в узлах. Итерации продолжаются до достижения корня и получения итогового множественного выравнивания. На заключительном этапе производится несколько итеративных выравниваний, целью которых является исправление позиций гэпов, возникших во время прогрессивного выравнивания.