Фурье

1. Задание функции

Использовался variant5.txt

2 линейные молекулы, четырехатомная молекула и двухатомная молекула. Атомы в каждой молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга.
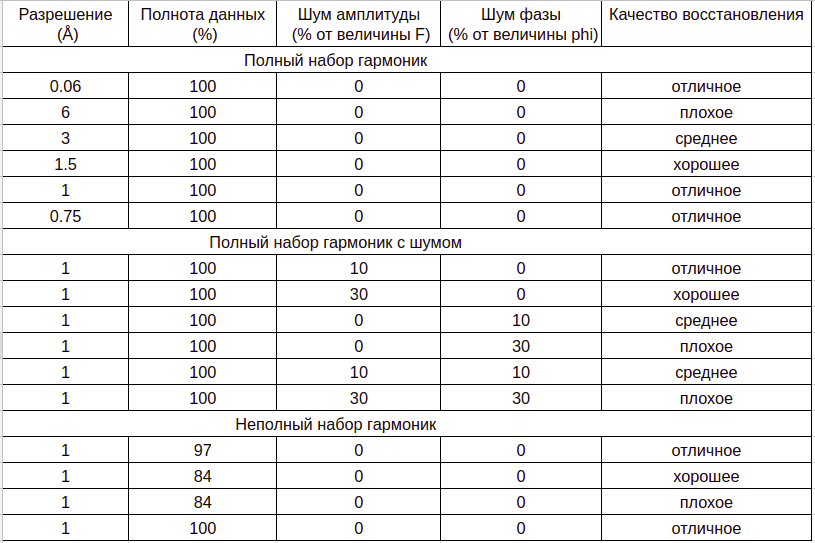
Далее была задана функция, моделирующаяся в 1D график электронной плотности молекулы, на интервале [0, 30] Å

Запустил скрипт compile-func.py. Результат - func.txt и следующее изображение:

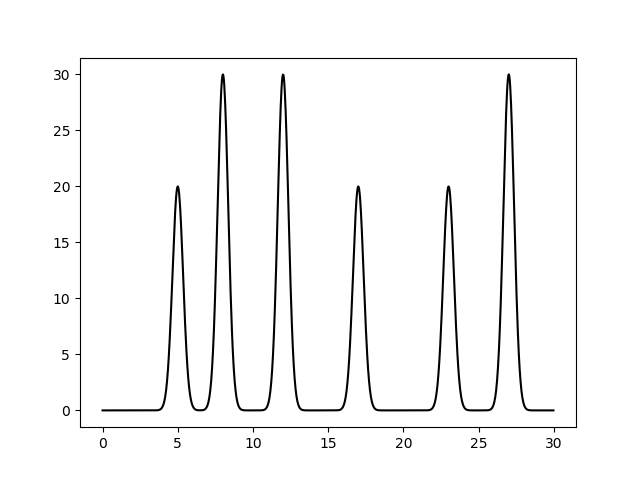
Рис.0. График функции электронной плотности модели атомов

2. Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные

Функция была разложена в ряд Фурье с помощью скрипта func2fourier.py. Результат - func_ft.txt (499 гармоник)

3. Восстановление функции ЭП по амплитудам и фазам части сигналов

Критерии качества восстановления
• Отличное восстановление – легко определить положение максимума всех атомов по графику восстановленной функции.
• Хорошее восстановление – можно предположить положения максимумов, зная число атомов, по восстановленной функции максимумы трудно отличить от шума.
• Среднее восстановление – есть атомы, положение которых определить по восстановленной функции нельзя, а есть те, у которых можно.
• Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер молекулы

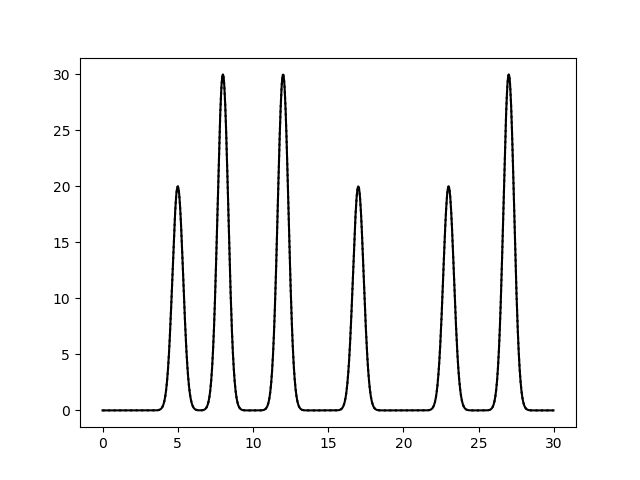
Рис.1. Восстановление функции по полному набору гармоник (0-498). выдача fourier2func. Восстановление отличное.

Отбор гармоник из полного набора произведен с помощью скрипта fourier-filter.py. Далее приведены результаты восстановления по первым 5, 10,..., 35, 40 гармоникам.

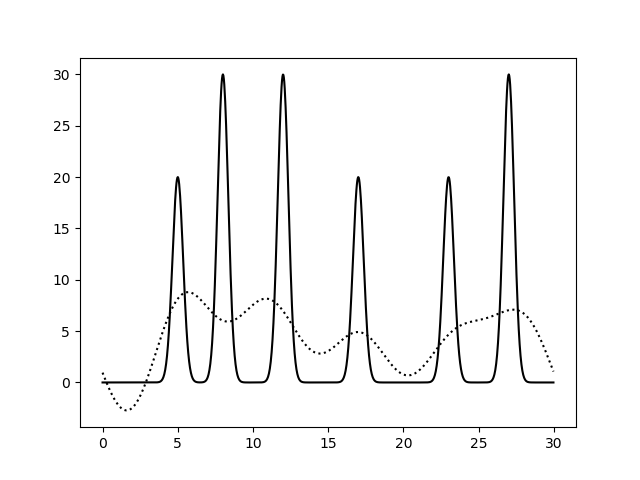
Рис.2. Восстановление функции по неполному набору гармоник (0-5). выдача fourier2func. Восстановление плохое.

Рис.3. Восстановление функции по неполному набору гармоник (0-10). выдача fourier2func. Восстановление среднее.

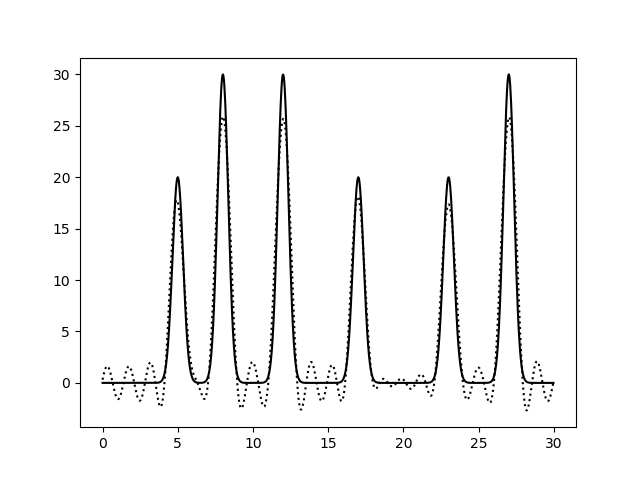
Рис.4. Восстановление функции по неполному набору гармоник (0-20). выдача fourier2func. Восстановление хорошее.

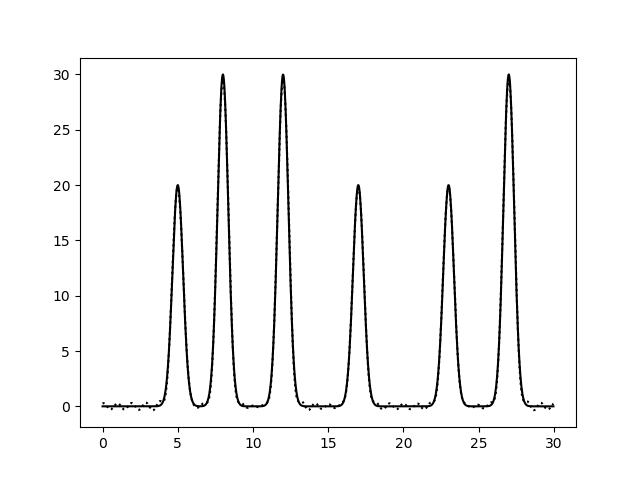
Рис.5. Восстановление функции по неполному набору гармоник (0-30). 0_30.txt. Восстановление отличное.

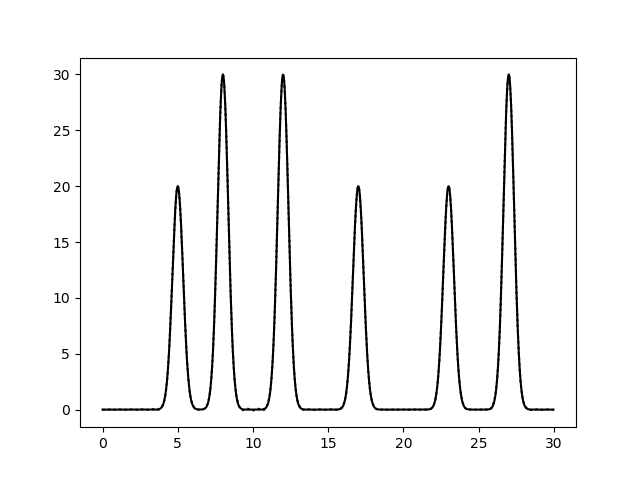
Рис.6. Восстановление функции по неполному набору гармоник (0-40). 0_40.txt. Восстановление отличное.

Добавление шума к амплитуде

Отличное восстановление получилось, например, для первых 31 гармоник. Вот что получается, если добавлять 10, 30% шума к амплитуде:

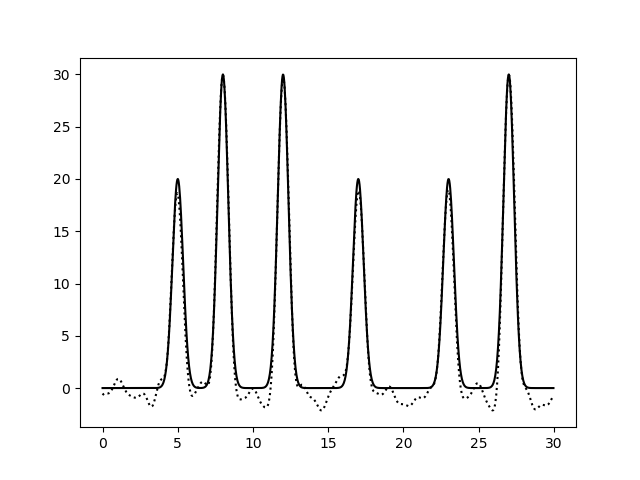
Рис.7. Восстановление функции по первым 31 гармоникам при добавлении 10% шума к амплитуде. выдача fourier-filter, выдача fourier2func . Восстановление отличное

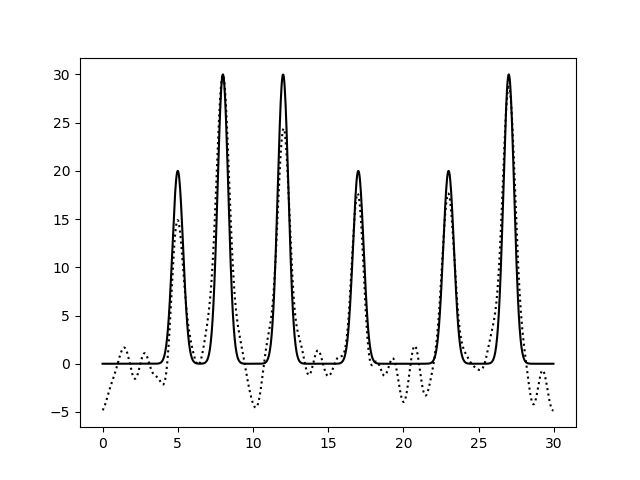
Рис.8. Восстановление функции по первым 31 гармоникам при добавлении 30% шума к амплитуде. выдача fourier-filter, выдача fourier2func . Восстановление хорошее

Добавление шума к фазе

Отличное восстановление получилось, например, для первых 31 гармоник. Вот что получается, если добавлять 10, 30% шума к фазам:

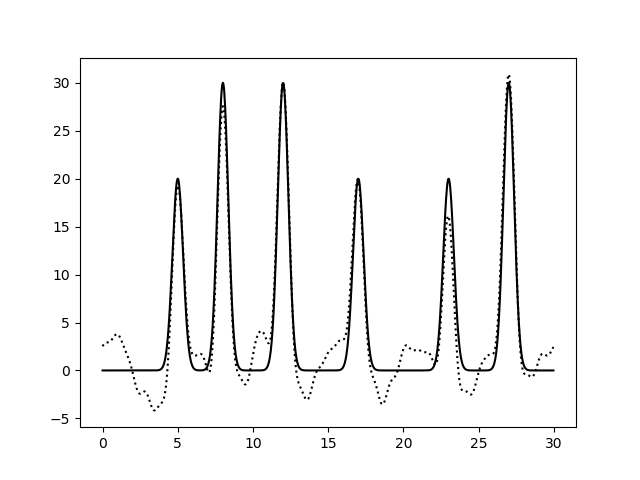
Рис.9. Восстановление функции по первым 31 гармоникам при добавлении 10% шума к фазам. выдача fourier-filter, выдача fourier2func . Восстановление среднее

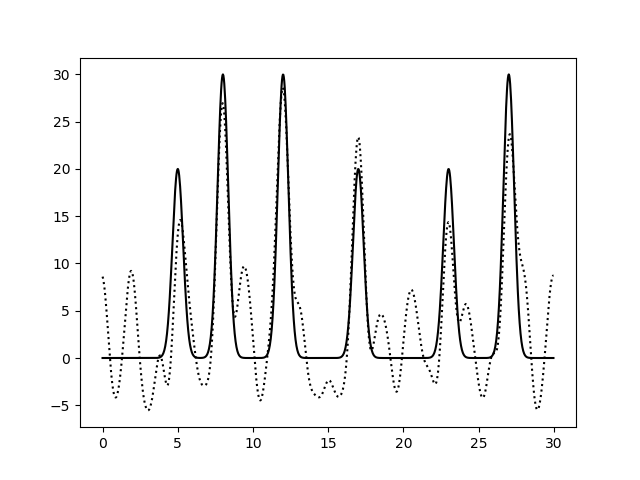
Рис.10. Восстановление функции по первым 31 гармоникам при добавлении 30% шума к фазам. выдача fourier-filter, выдача fourier2func . Восстановление плохое

Видно, что шум в фазах вносит намного больший вклад, чем шум в амплитудах.

Добавление шума и к фазе, и к амплитуде

Отличное восстановление получилось, например, для первых 31 гармоник. Вот что получается, если добавлять 10, 30% шума и к фазам, и к амплитудам:

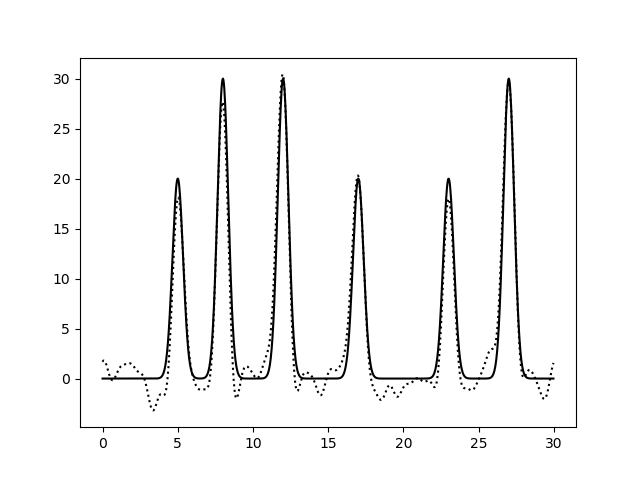
Рис.11. Восстановление функции по первым 31 гармоникам при добавлении 10% шума и к фазам, и к амплитудам. выдача fourier-filter, выдача fourier2func . Восстановление среднее

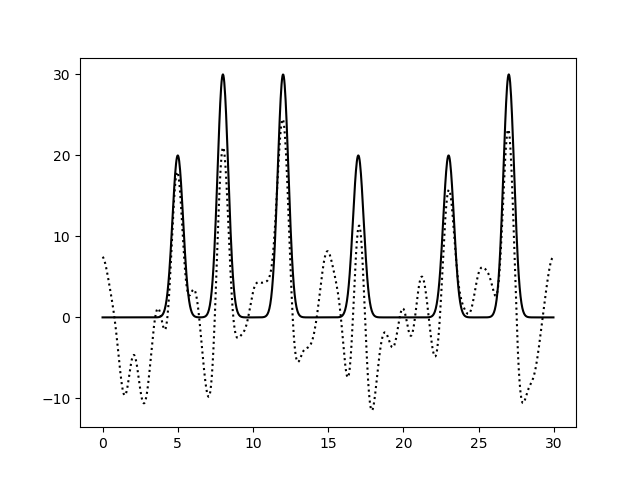
Рис.12. Восстановление функции по первым 31 гармоникам при добавлении 30% шума и к фазам, и к амплитудам. выдача fourier-filter, выдача fourier2func . Восстановление очень плохое

Неполные наборы гармоник

Вот что получается при использовании неполных наборов гармоник с удаленными первыми или средними гармониками или добавленной 40 гармоникой:

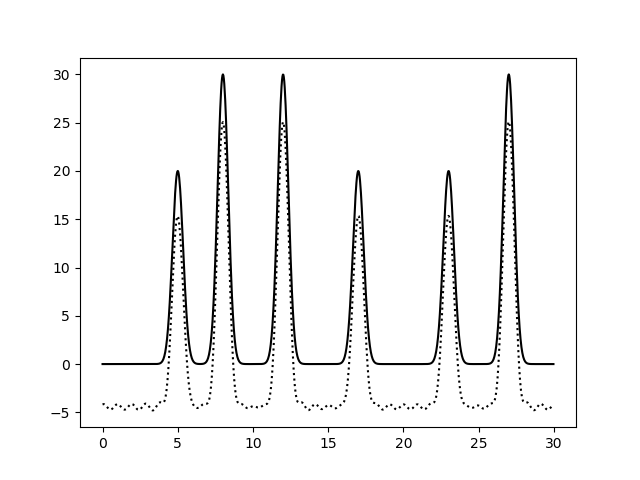
Рис.13. Восстановление функции по неполному набору гармоник (1-30). выдача fourier2func. Восстановление отличное.

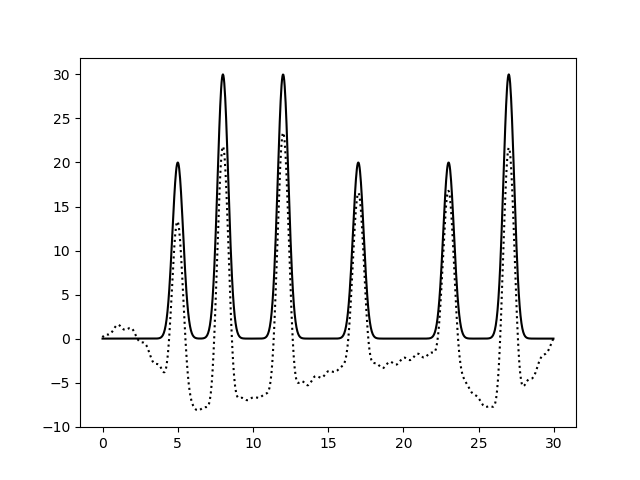
Рис.14. Восстановление функции по неполному набору гармоник (0-5). выдача fourier2func. Восстановление хорошее.

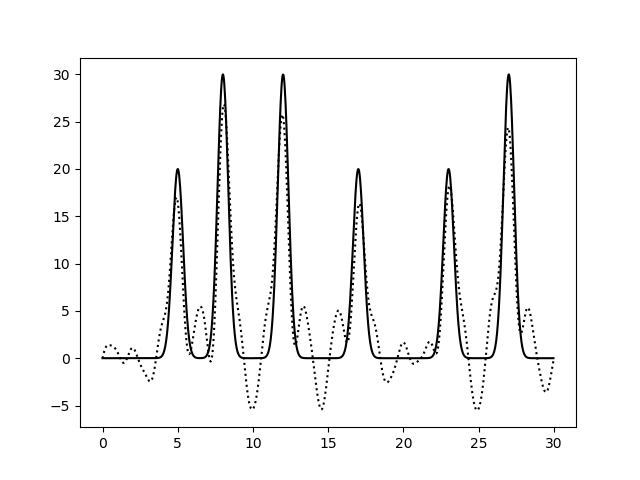
Рис.15. Восстановление функции по неполному набору гармоник (0-10, 16-30). выдача fourier2func. Восстановление плохое.

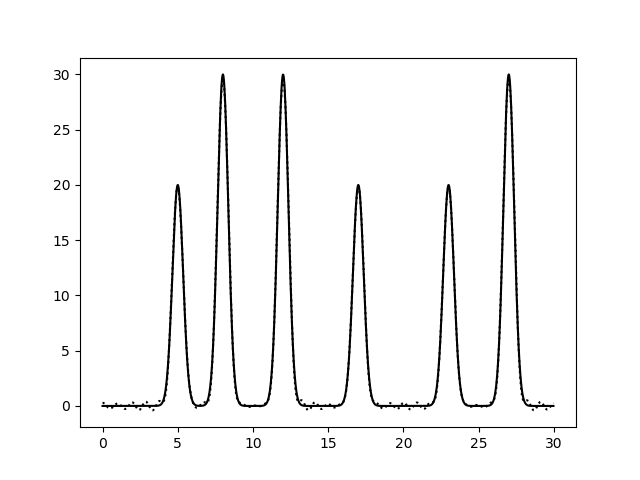
Рис.16. Восстановление функции по набору гармоник (0-30, 40). выдача fourier2func. Восстановление отличное, не отличимое от восстановления 0-30.

Видимо, высокий вклад в качество имеют гармоники в середине набора

4. Итог