| Главная | Семестры | Обо мне | Ссылки |
|---|
Восстановление электронной плотности по данным РСА: одномерная модель
Создание модели и задание функции
Для выполнения задания я выбрала данные, удовлетворяющие всем условиям:
- На отрезке [0,30] (ангстремы) расположены две молекулы.
- Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга.
- Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними).
- Всего 5-7 атомов (2+3 или 2+3+2; возможны другие варианты).
- Электронные плотности (ЭП) атомов описываются гауссовой кривой.
- Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.
Для этих данных была построена одномерная функция электронной плотности с помощью скрипта compile-func.py.
python compile-func.py -g 20,2,5+30,2,8+30.0,2,12+20.0,2,17+20.0,2,23+30,2,27
График электронной плотности модели атомов представлен на рисунке 1. Поточечные координаты приведены в файле func.txt.
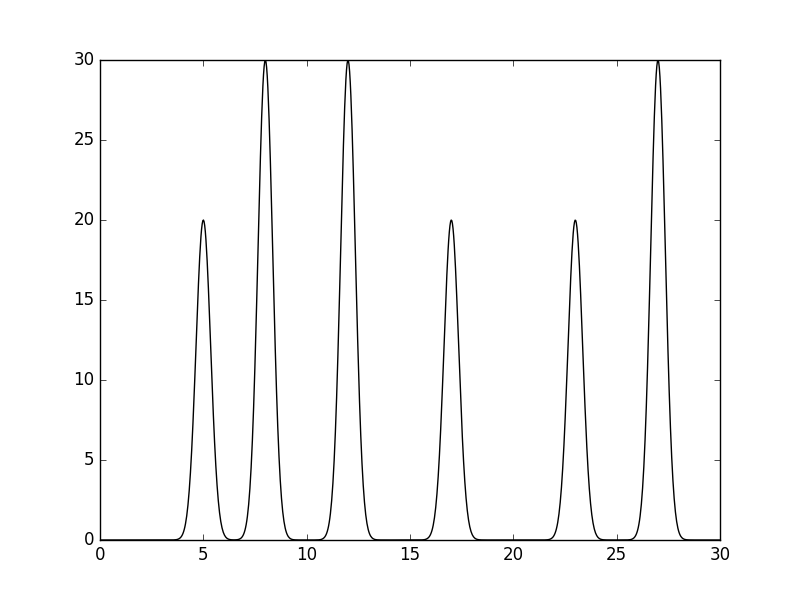
Рис. 1. График электронной плотности линейной модели атомов.
Расчёт коэффициентов Фурье
Коэффициенты Фурье рассчитываются с помощью скрипта func2fourier.py. Скрипт раскладывает полученный ранее файл func.txt на 499 гармоник на отрезке [0 Å, 30 Å], выдает их в файле func_ft.txt.
python func2fourier.py -i func.txt
Восстановление функции ЭП по амплитудам и фазам
Восстановление функции по отобранным гармоникам выполняется скриптом fourier2func.py, который выдает текстовый и графический файлы с исходной и восстановленной функцией.
func.txt - файл с функцией
func_ft.txt - файл с отобранными коэффициентами Фурье
output_name.txt - файл для результата в текстовом формате
python fourier2func.py -f func.txt -i func_ft.txt -o output_name.txt
Полный набор гармоник
При полном наборе из 500 коэффициентов Фурье функция восстанавливается на 100%. Как видно на рис. 2, графики восстановленной и исходной функции идентичны.
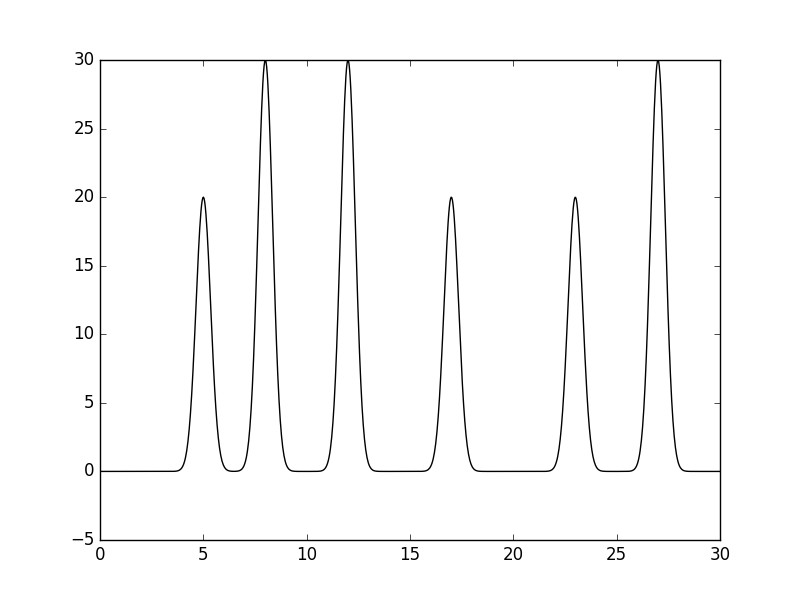
Рис. 2. Восстановленная по полному набору коэффициентов Фурье функция электронной плотности
Далее введем критерии сравнения восстановленной функции с исходной.
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"
Найдем набор гармоник, при котором сохранится отличное восстановление функции ЭП. На рис. 3 приведены примеры ко всем видам восстановления функции, от плохого (рис. 3А) до отличного (рис. 3Г). При первых одиннадцати гармониках (рис. 3Д) формально можно указать отличное восстановление, так как положение максимумов всех атомов различить можно. Но ширина пиков и положение максимумов заметно отличается от исходной функции. Поэтому я решила, что стоит добиться полного совпадения ширины пиков. Таким образом, отличное восстановление функции достигается при числе гармоник, равном 20.
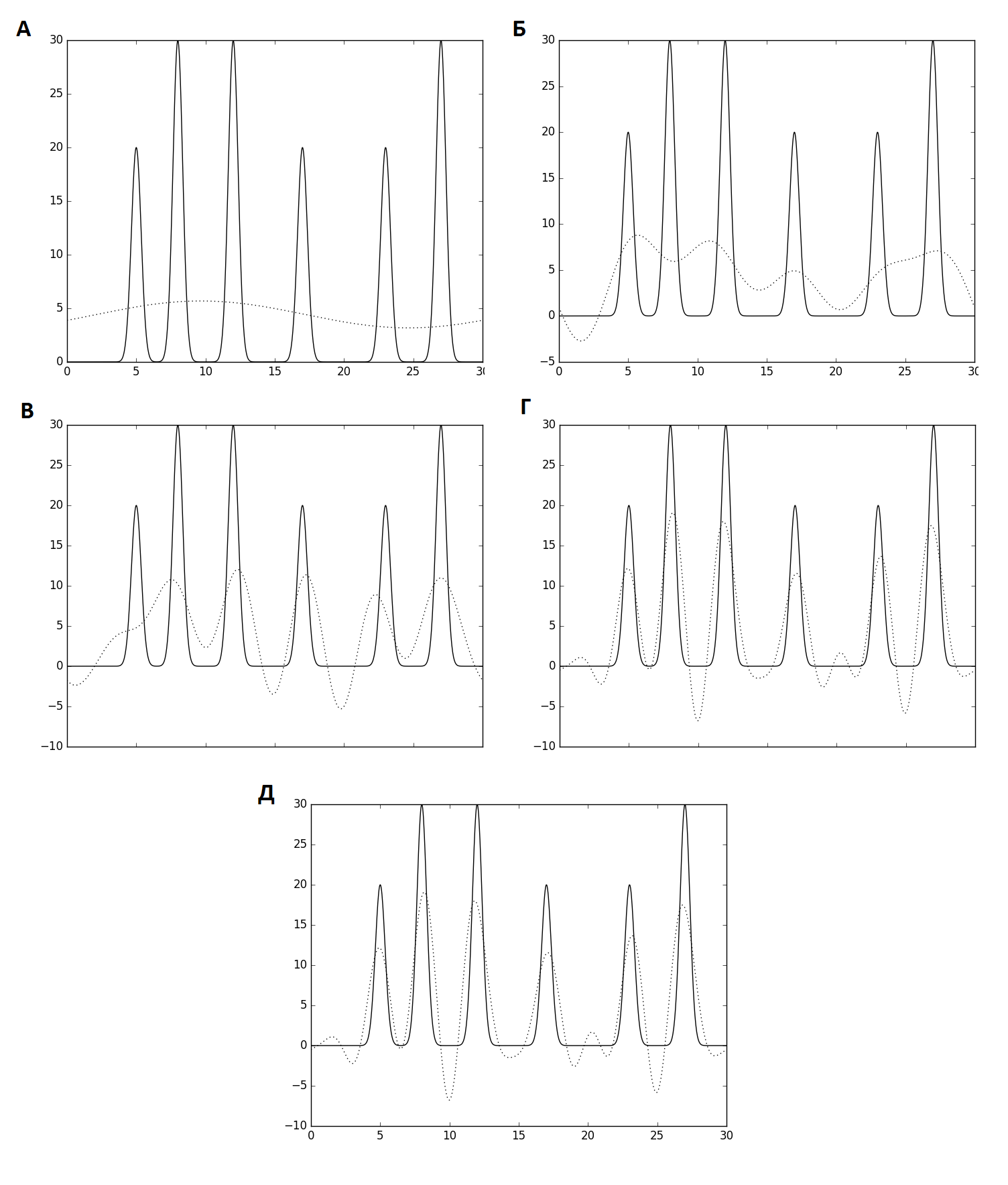
Рис. 3. Восстановление функции ЭП: плохое при первых двух гармониках (А), среднее при первых шести гармониках (Б), хорошее при первых восьми гармониках (В), отличное при первых двадцати гармониках (Г), хорошее при одиннадцати гармониках (Д).
Рассмотрим, какое восстановление будет по первым 20 гармоникам, при добавлении шумов к амплитуде, фазе, или к обоим параметрам (рис. 4). Результаты приведены в таблице 1. Стоит отметить, что шум в фазах вносит гораздо больший вклад в изменения, чем шум в амплитудах.
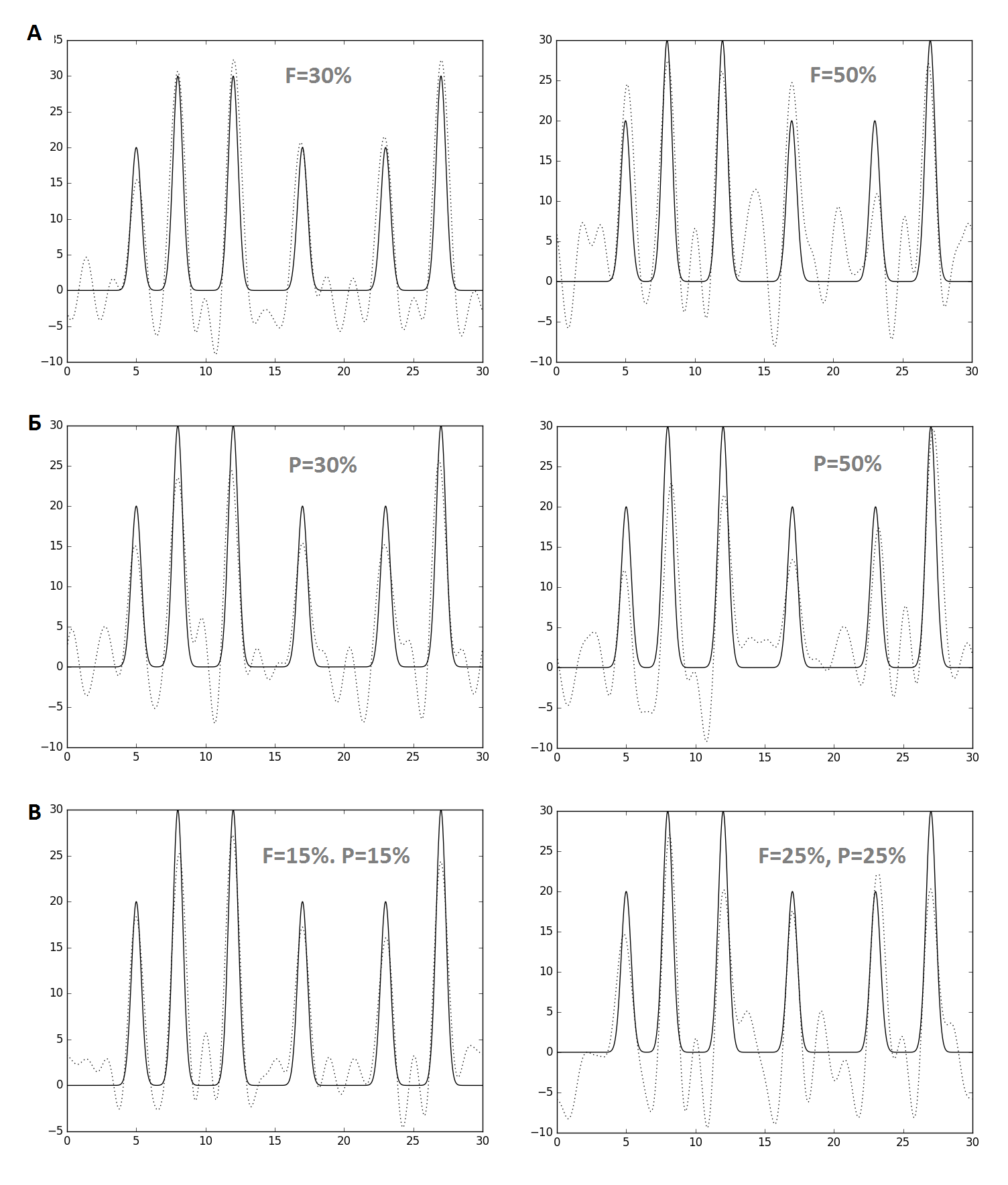
Рис. 4. Восстановление функции ЭП по 20 гармоникам с добавлением шума к амплитуде (А), шуму (Б), к амплитуде и шуму (В).
Неполные наборы гармоник
Набор гармоник ряда Фурье называется полным, если известны все гармоники с номерами 0, 1, 2, ..., n. Посмотрим, что будет с восстановлением функции, если из набора первых 20 удалить часть гармоник (рис. 5).
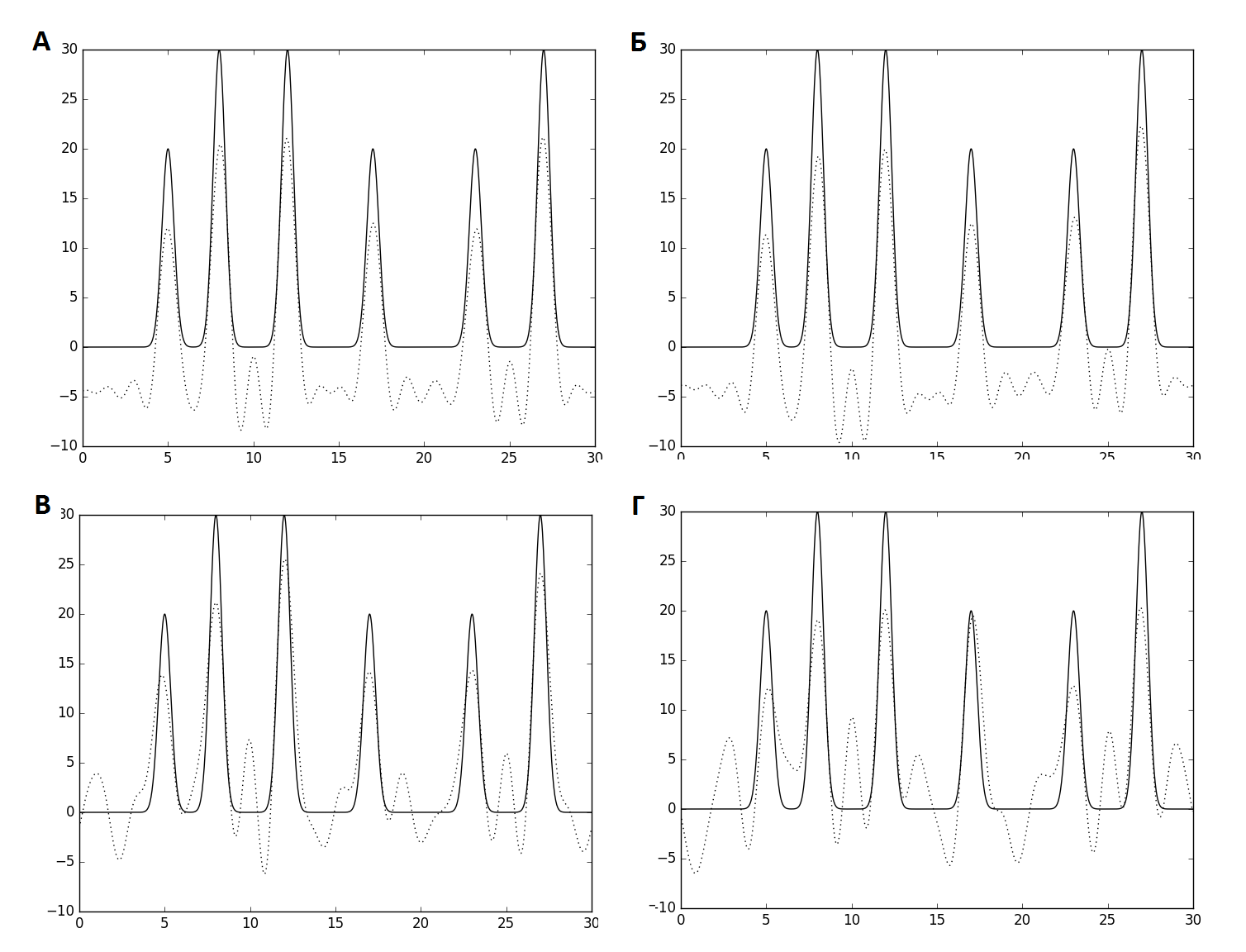
Рис. 5. Восстановление функции ЭП по неполному набору гармоник: без гармоники с номером 0 (А), без первых двух гармоник (Б), без двух гармоник из середины набора (В,Г).
При удалении гармоники с номером 0, очевидно, наблюдаем сдвиг графика на константу. Однако, при этом функция восстанавливается отлично. То же наблюдается при удалении первых двух гармоник: ширина пиков и положение максимумов практически не отличаются от исходной функции. Если удалить 10% гармоник из середины, качество восстановления заметно ухудшилось, причем настолько, что максимумы от «атомов» стали менее отличимы от шума.
Если к набору из 20 гармоник добавить 30-ю гармонику, то заметных изменений мы не увидим (рис. 6). Наблюдается отличное восстановление функции, чего и следовало ожидать.
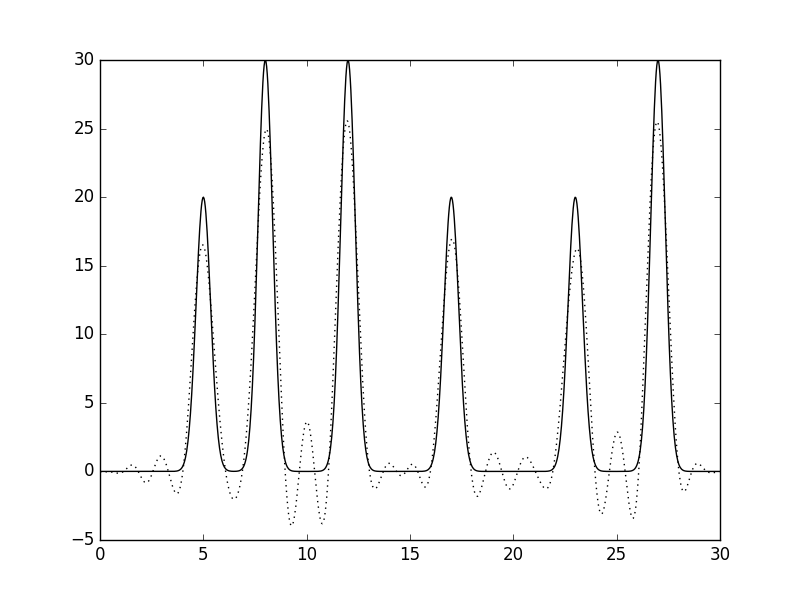
Рис. 6. Восстановление функции ЭП по набору гармоник 0-19,29.
Как определить разрешение набора гармоник?
Для полного набора гармоник разрешение - это период наиболее высокочастотной гармоники. В нашем случае, если в наборе 499 гармоник, то разрешение будет d=T/n: 30 Å / 499 = 0,06 Å. Отличное восстановление функции ЭП в данной работе получается при разрешении 30 Å / 20 = 1,5 Å.
Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо сообщить полноту данных — процент гармоник с длиной волны большей d от максимально возможного, присутствующих в наборе. Для полного набора данных (разрешение d=T/n) полнота равна 100%. Если хочется сравнивать разрешения структур, то можно выбрать порог по полноте данных, определить максимальный набор гармоник с полнотой не меньше пороговой и найти в этом наборе наиболее высокочастотную гармонику. Например, рассмотрим данные на рис. 7. Разрешение этой структуры можно принять таким:
- 1 Å с полнотой данных 18/31*100% = 58%
- 1.5 Å с полнотой 17/21 *100% = 70%
- 2 Å с полнотой 16/19 *100% = 84%
В нашем случае неполных наборов гармоник минимальная полнота набора составила 90% при удалении двух гармоник. Мне кажется, в таком случае не стоит увеличивать величину разрешения, а лишь указать полноту данных. В случае добавления 30-й гармоники можно было бы пересчитать разрешение как период этой самой гармоники, оно составило бы 1 Å, но при полноте данных 70%.

Рис. 7. Иллюстрация неполного набора гармоник. Кружок соответствует гармонике. Каждая гармоника имеет свой номер и период. Кружок отложен на оси в соответствии с периодом, периоды подписаны снизу. Красные кружки соответствуют измеренным структурным факторам, синие - не измеренным.
Результаты
Все результаты, полученные в течение выполнения данной работы, сведены в таблицу 1.
Таблица 1. Восстановление функции ЭП по коэффициентам Фурье
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум амплитуды (% от величины F) | Шум фазы (% от величины phi) | Качество восстановления (отличное, хорошее, среднее, плохое) | Комментарии |
|---|---|---|---|---|---|---|
| Полный набор гармоник | ||||||
| 0-1 | 30 Å | 100% | 0 | 0 | Плохое | |
| 0-5 | 6 Å | 100% | 0 | 0 | Среднее | |
| 0-7 | 4,3 Å | 100% | 0 | 0 | Хорошее | |
| 0-10 | 3 Å | 100% | 0 | 0 | Хорошее | Будем считать такое восстановление хорошим, а не отличным |
| 0-19 | 1,6 Å | 100% | 0 | 0 | Отличное | |
| 0-19 | 1,6 Å | 100% | 30 | 0 | Хорошее | |
| 0-19 | 1,6 Å | 100% | 0 | 30 | Хорошее | |
| 0-19 | 1,6 Å | 100% | 15 | 15 | Хорошее | |
| 0-19 | 1,6 Å | 100% | 50 | 0 | Среднее | Получился «шумовой» пик, который выше одного из реальных пиков |
| 0-19 | 1,6 Å | 100% | 0 | 50 | Среднее | |
| 0-19 | 1,6 Å | 100% | 25 | 25 | Хорошее | |
| Неполный набор гармоник | ||||||
| 1-19 | 1,6 Å | 95% | 0 | 0 | Отличное | |
| 2-19 | 1,6 Å | 90% | 0 | 0 | Отличное | |
| 0-9,12-19 | 1,6 Å | 90% | 0 | 0 | Хорошее | |
| 0-7,10-19 | 1,6 Å | 90% | 0 | 0 | Среднее | |
| 0-19, 30 | 1,6 Å | 100% | 0 | 0 | Отличное | Странно было бы ожидать иного результата |