Восстановление функции электронной плотности преобразованиями Фурье




Ход работы

Целью данной работы является изучение зависимости качества восстановления данных из разложения Фурье от количества и качества (какие именно) используемых гармоник ряда.
Задание включает следующие этапы:

  1. Создание модельной одномерной функции электронной плотности
  2. Разложение Фурье модельной функции: расчет амплитуд и фаз
  3. Фильтрация гармоник
  4. Обратное преобразование Фурье: восстановление ЭП по неполному набору данных
  5. Оценка качества восстановления функции ЭП

Задание функции ЭП

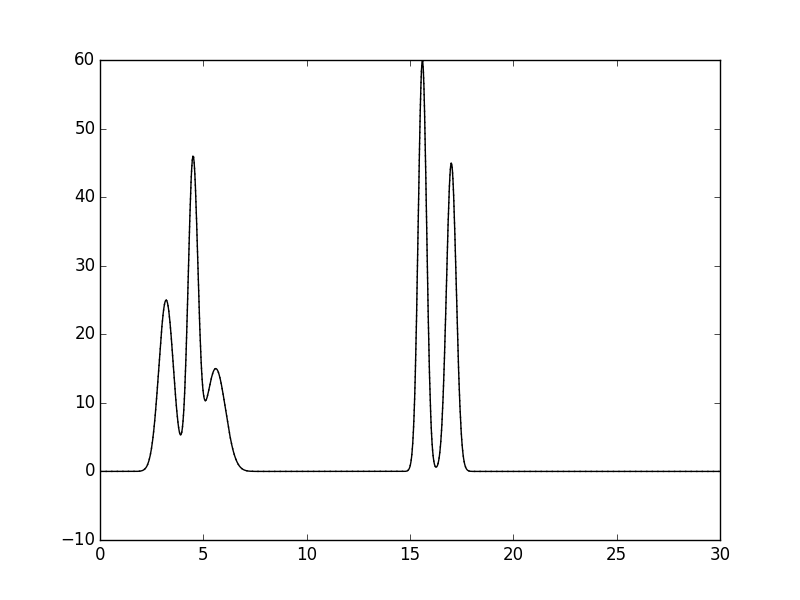
При помощи скрипта compile-func.py была создана гипотетическая одномерная модель, состоящая из трехатомной и двухатомной молекул (Рис. 1).
На вход скрипту подаются тройки параметров (λ, β, γ), каждая тройка характеризует отдельный атом, согласно гауссиане:

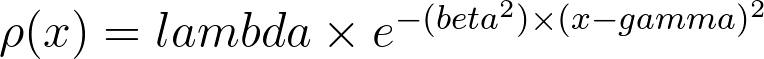
Параметр λ - амплитуда пика, β - ширина пика, γ - координата максимума. Таким образом, скрипт создает сумму заданных гауссиан.

Пример задания ЭП: 

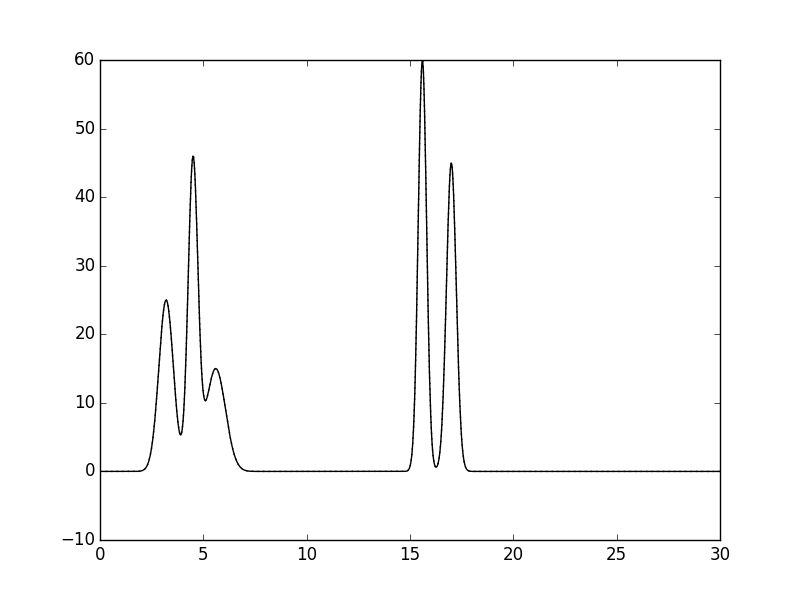
D:\...\python.exe compile-func.py -g 25,2,3.2+45,3,4.5+15,1.5,5.6+60,3.5,15.6+45,3,17 -o e_function.txt
На выходе, скрипт выдает таблицу видa X, Y, где X - координата, а Y - значение ЭП, а также график ЭП (Рис. 1).

Рисунок 1. Электронная плотность двух линейных молекул. По Х - координаты (Å), по Y - амплитуда ЭП (у.е.)

Разложение ЭП в ряд Фурье

Вторым шагом, функцию электронной плотности разложили в ряд Фурье при помощи скрипта func2fourier.py, на вход которому подается таблица ЭП, полученная на шаге 1.

Пример запуска скрипта: 

D:\...\python.exe func2fourier.py -i e_function.txt -o fourier_full.txt
На выходе мы получаем таблицу гармоник вида (№, F, φ), где № - номер гармоники, F - амплитуда, φ - фаза.

Фильтрация гармоник

Для исследования зависимости качества восстановления функции ЭП от количества и качества гармоник разложения Фурье, были проведены следующие манипуляции с данными:

Усеченные ряды создавались вручную, удалением ненужных строк из файла с гармониками. Шум добавляли скриптом func2fourier.py параметрами -F - шум для амплитуд -P - шум для фаз: 
D:\...\python.exe func2fourier.py -i e_function.txt -o fourier_full.txt -F 10 -P 10

Восстановление ЭП

Восстановление ЭП по набору гармоник (обратное преобразование Фурье) проводилось скриптом fourier2func.py. 

D:\...\python.exe fourier2func.py –f e_function.txt –i fourier_set.txt -0 e_func_vs_fourier_set.txt –p e_map_vs_fourier_set.png
На вход скрипту подается оригинальная функция ЭП и набор гармоник, на выходе получаем таблицу с двумя функциями - полной ЭП и восстановленной, а также изображение с соответствующими графиками ЭП.

Результаты. Оценка качества восстановления

Полные наборы гармоник

Как уже было сказано, полный набор содержит 499 гармоник. Восстановление из такого набора идеально (Рис. 2а). Если добавить 10 процентный шум по амплитудам, то возникают незнаительные флуктуации, и можно однозначно указать положение и характер атомов (Рис. 2б). 10 процентный шум по фазам дает чуть большие по амплитуде случайные флуктуации, однако и здесь можно безошибочно восстановить исходную картину (Рис. 2в). Интересно, что совместный 10 процентный шум и по фазам, и по амплитудам, на взгляд, находится по интенсивности в промежутке между только амплитудами и только фазами (Рис. 2г). В последнем случае также можно восстановить исходную картину.


а б в г

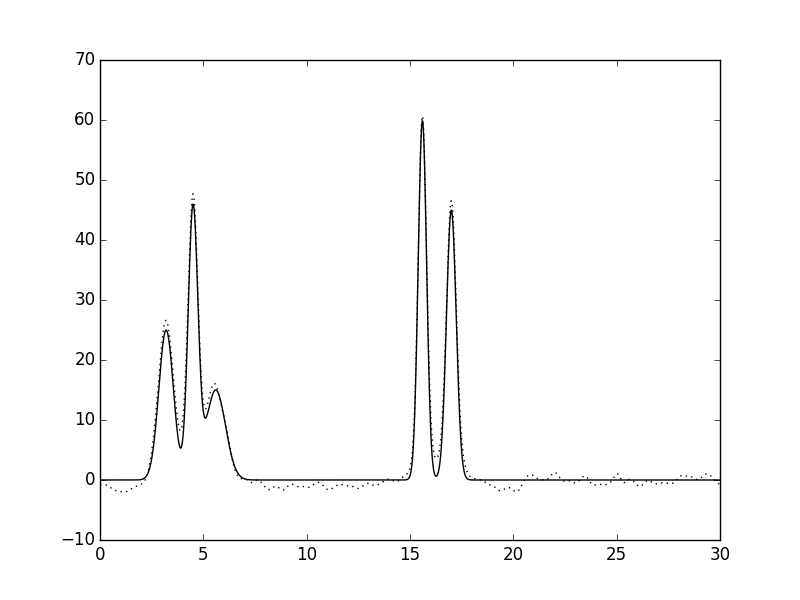
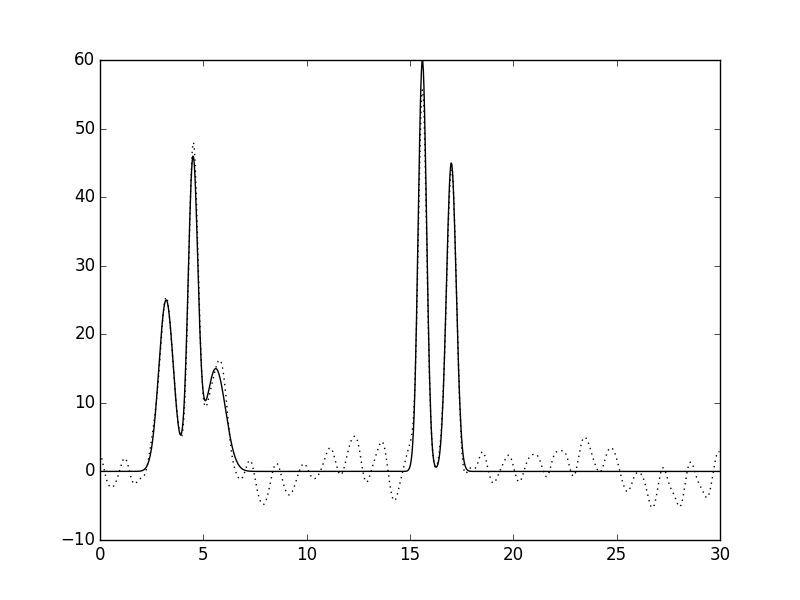
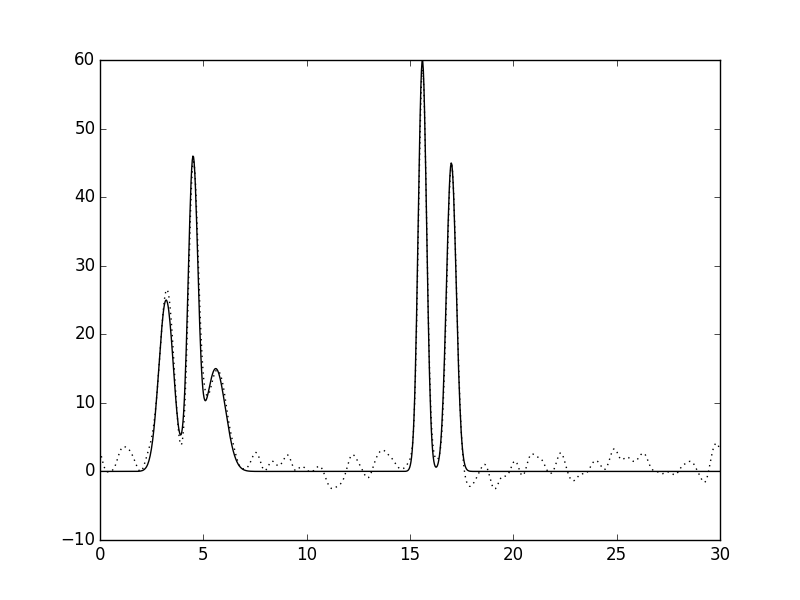
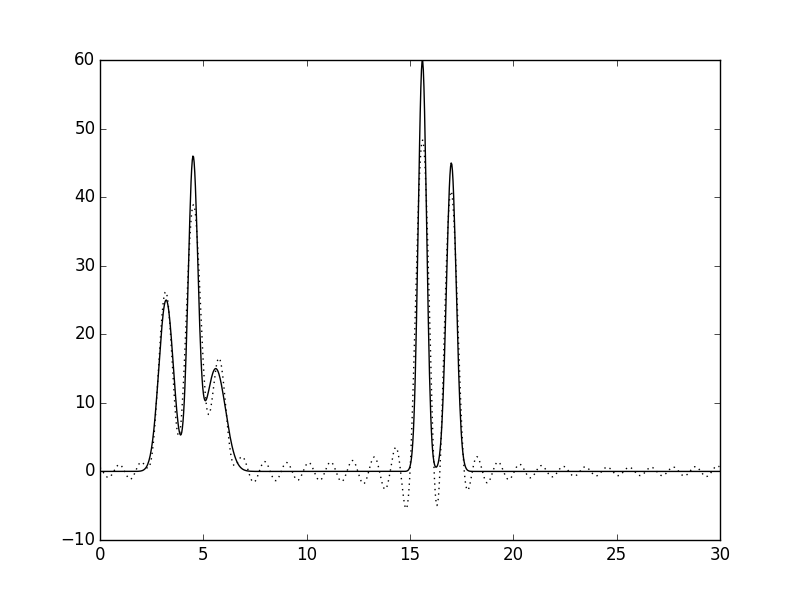
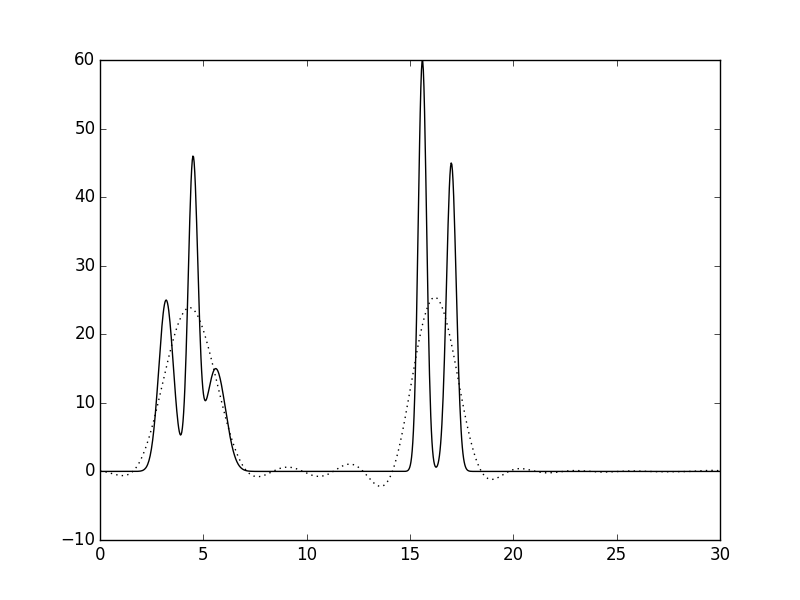
Рисунок 2. Восстановление функции ЭП из полного набора гармоник. а. Полный набор гармоник без шумов. б. Шум по амплитудам 10%. в. Шум по фазам 10%. г. Шум по и по фазам, и по амплитудам 10%

Неполные наборы гармоник

Усечение набора с конца

ЭП, восстановленная из набор 250 первых гармоник разложения Фурье, с виду ничем не отличается от оригинальной (Рис. 3а). Точность восстановления удивительным образом сохряняется и для набора из первых 31 гармоники. Восстановленная функция не такая гладкая, как исходная, но по ней можно однозначно установить положения всех атомов Рис. 3б. Хуже дело обстоит для первых 11 гармоник. В этом случае мы можем указать положение молекул, но их структура для нас не доступна (Рис. 3в). И совсем плохая картина для первых двух гармоник (нулевой и первой) - здесь можно угадать только положение молекулярного кластера и то, недостаточно однозначно (Рис. 3г).


а б в г

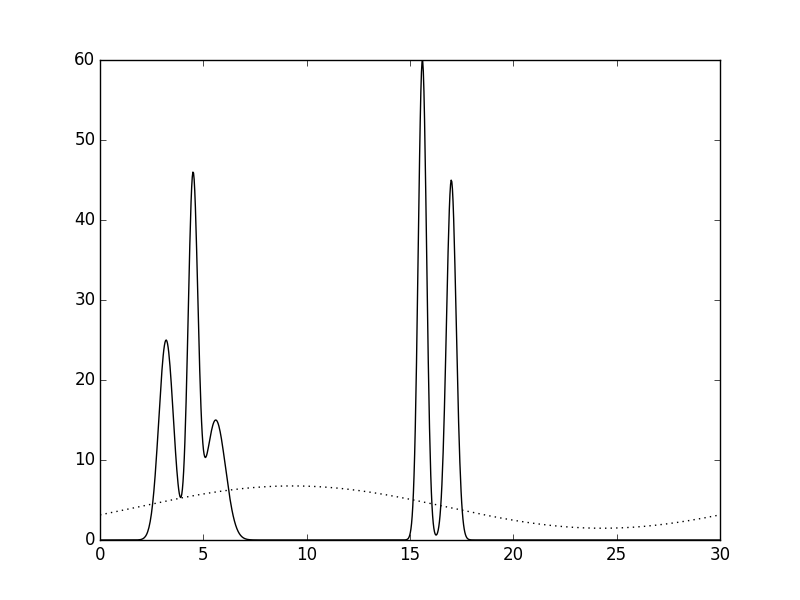
Рисунок 3. Восстановление функции ЭП из неполного набора гармоник. Усечение с конца.а. Первые 250 гармоник. б. Первые 31 гармоника. в. Первые 11 гармоник. г. Первые 2 гармоники

Усечение набора с двух сторон

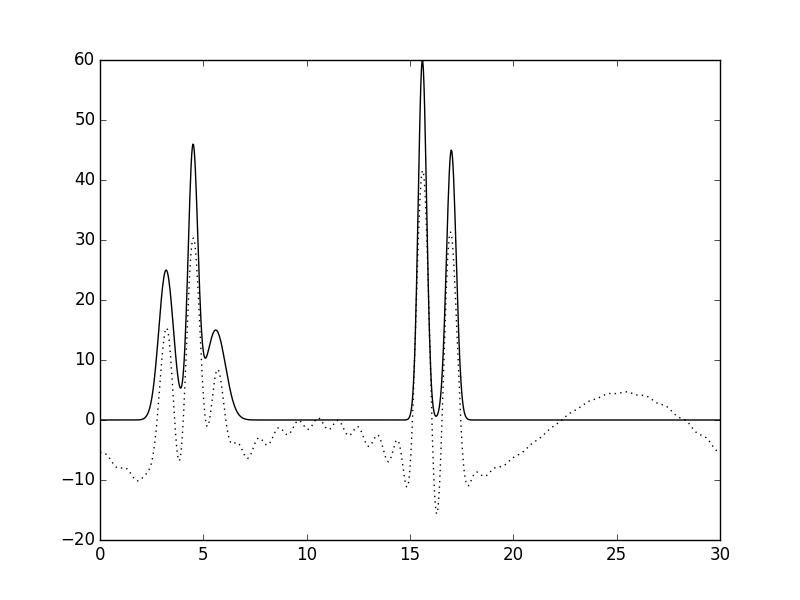
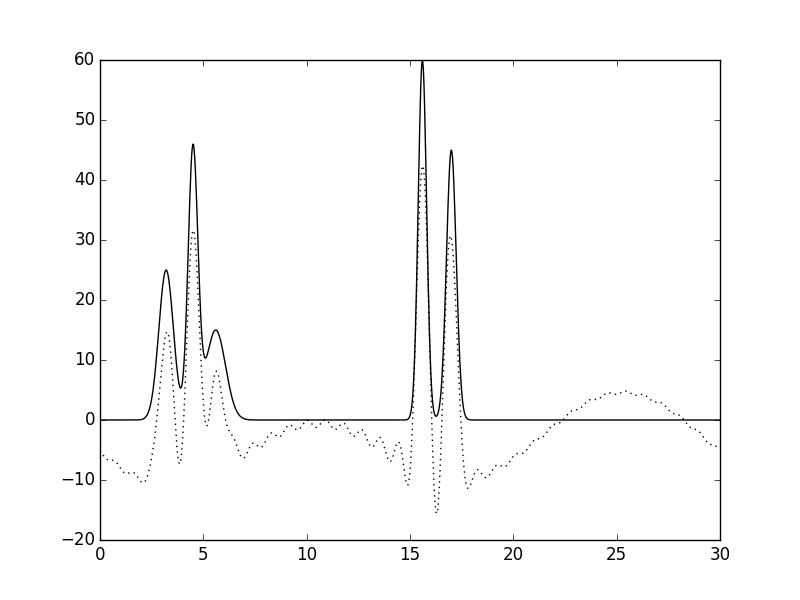
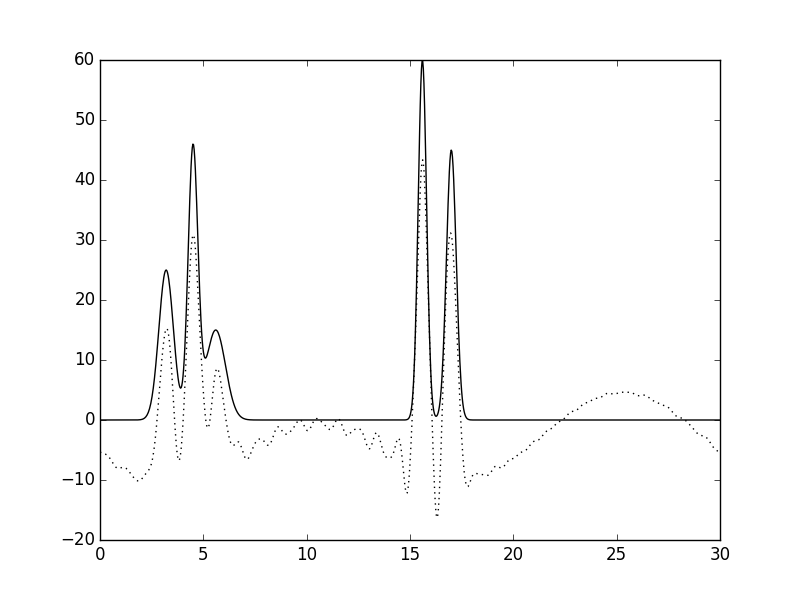
Посчитав точность, получаемую при восстановлении функции ЭП из первых 31 гармоники удовлетворительной (Рис. 4а), было исследовано влияние низких гармоник на качество восстановления. Для этого, были удалены первые 3 гармоники (Рис. 4б). Заметно, что качество значительно пострадало, например, в области 25 Å появился горб, который легко можно спутать с молекулой. При восстановлении длины набора до 31 гармоники (3-33 гармоники) картина меняется незначительно и никак не улучшается (Рис. 4в).Также дело обстоит, если добавить набор более высоких гармоник (3-33 + 50-80) (Рис. 4г). Можно заключить, что низкие гармоники важнее для восстановления общего вида структуры, и высокие гармноники не могут заменить их при потере.


а б в г

Рисунок 4. Восстановление функции ЭП из неполного набора гармоник. Усечение с обоих сторон. а. Первые 31 гармоника. б. Гармоники с 3 по 30. в. Гармоники с 3 по 33. г. Гармоники с 3 по 33 и с 50 по 80

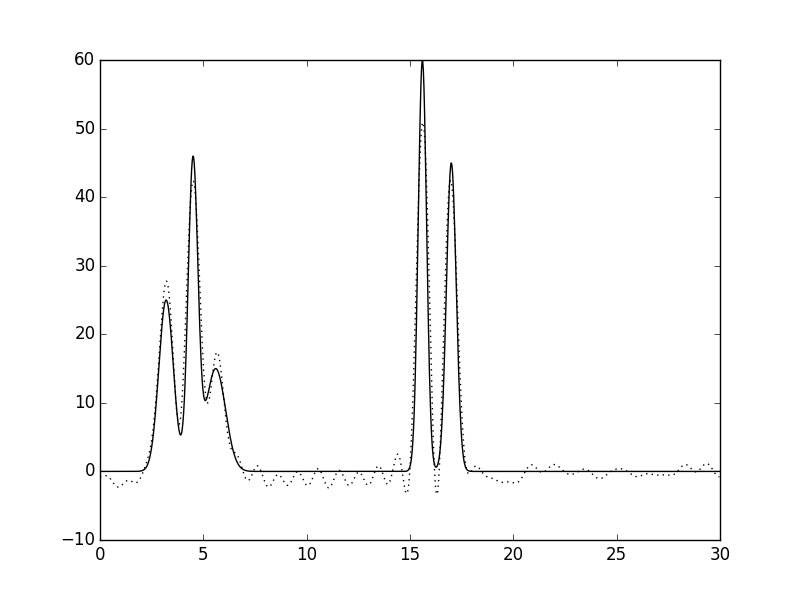
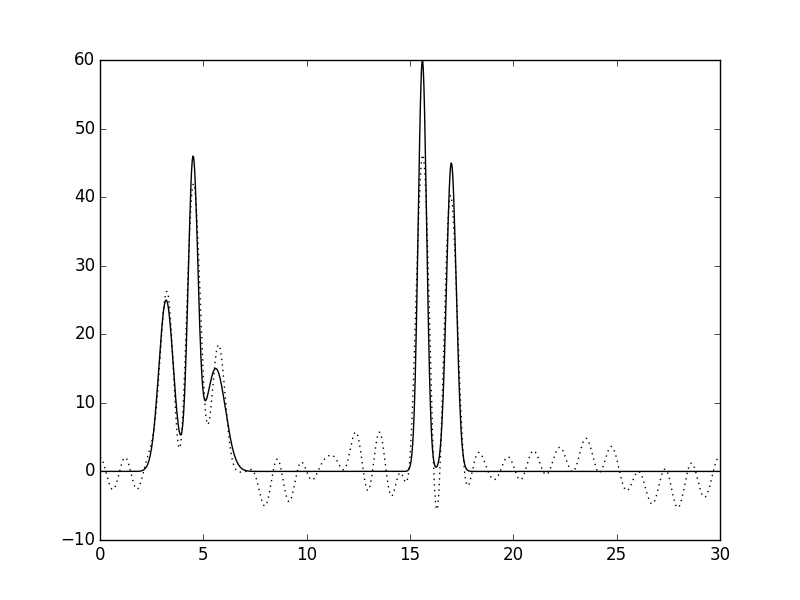
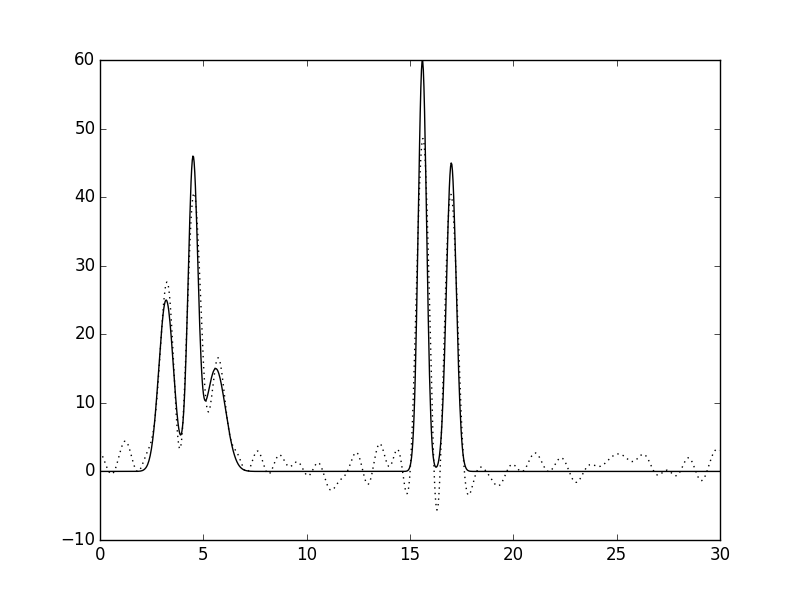
Применение шума к усеченному набору

По уже высказанным соображениям, влияние шума на восстановление ЭП исследовалось для набора из первых 31 гармоники (Рис. 5а). 10 процентный шум по амплитуде практически никак не сказался на качестве восстановления (Рис. 5б). После внесения 10% шума по фазе также можно восстановить исходную структуру, однако отдельные флуктуации уже можно спутать с легкими атомами (Рис. 5в, между 10 и 15 Å). Одновременный шум и по фазе, и по амплитуде, как уже было отмечено для полного набора гармоник, немного погасили друг друга, так что в этом случае структура восстанавливается практически безошбочно (Рис. 5г).


а б в г

Рисунок 5. Восстановление функции ЭП из неполного набора, состоящего из первых 31 гармоники. а. Без шума. б. Шум по амплитуде 10%. в. Шум по фазе 10%. г. Шум 10% и по амплитуде, и по фазе

Полные результаты собраны в Таблице 1.
Набор гармоник Разрешение
(Å)		 Полнота данных
(%)		 Шум амплитуды
(% от величины F)		 Шум фазы
(% от величины phi)		 Качество восстановления
Полный набор гармоник
0-498 (полный) 0.06 100 0 0 Идеальное
0-498 (полный) 0.06 100 10 0 Отличное
0-498 (полный) 0.06 100 0 10 Хорошее
0-498 (полный) 0.06 100 10 10 Отличное
Усеченный с конца набор гармоник
0-250 0.12 100 0 0 Идеальное
0-30 1 100 0 0 Хорошее
0-10 3 100 0 0 Плохое
0-1 30 100 0 0 Отсутствует
Усечение с двух сторон; влияние низких гармоник
3-30 1 90 0 0 Удовлетворительное
3-33 0.91 90 0 0 Удовлетворительное
3-33+50-80 0.38 100 0 0 Удовлетворительное
Влияние шума
0-30 1 100 0 0 Хорошее
0-30 1 100 10 0 Хорошее
0-30 1 100 0 10 Удовлетворительное
0-30 1 100 10 10 Хорошее

Все данные (ряды Фурье и восстановленные функции ЭП) можно скачать в виде архива по ссылке.

Выводы