Восстановление одномерной функции электронной плотности
Задание состояло из нескольких этапов:
- Создание модельной функции ЭП в одномерной элементарной ячейке
- Расчет параметров сигнала, моделирующих экспериментальные данные: амплитуды и фазы
- Восстановление функции ЭП по "экспериментальным" данным
- Оценка качества восстановления
Для работы использовались следующие скрипты. В качестве модели для эксперимента были выбраны две молекулы, образующие водородную связь: HCN и HOH. Всего 6 атомов. Длины ковалентных связей: C-H — 1.068, C-N — 1.156, O-H — 0.991 [1,2]. На рис. 1 показано предполагаемое расположение молекул.
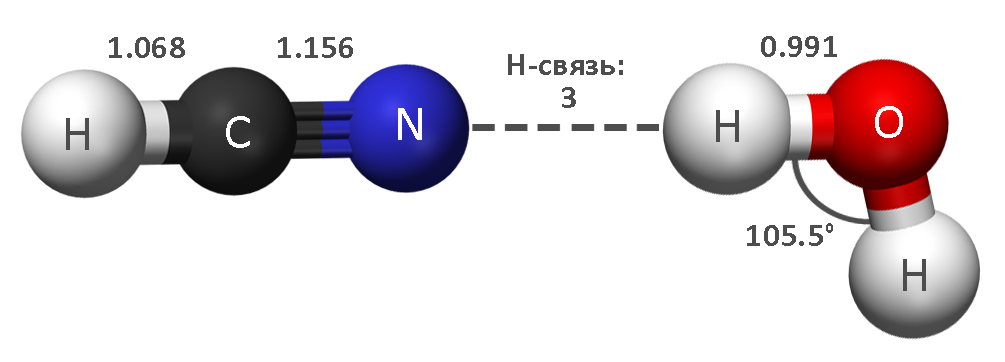
Рисунок 1. Экспериментальная модель двух молекул: HCN и HOH.
[1] Tables of Interatomic Distances and Configuration in Molecules and Ions, L.E. Sutton, ed., London: The Chemical Society, 1958.
[2] P. L. Silvestrelli and M. Parrinello, Structural, electronic, and bonding properties of liquid water from first principles, J. Chem. Phys. 111, 3572-3580, 1999.
Создание модельной функции ЭП
Функция была задана на интервале [0,30] с помощью следующей команды:
python compile-func.py -g 1,3,12+6,3,13.07+7,3,14.23+1,3,17.23+8,3,18.23+1,3,19.23Полученная функция является суммой гауссовых функций, где 12, 13.07, 14.23, 17.23, 18.23, 19.23 — центры атомов, а 1, 7, 1, 8, 1 — высоты пиков (у водородов они наименьшие и равны 1). На рис. 2 представлен вид полученной функции.
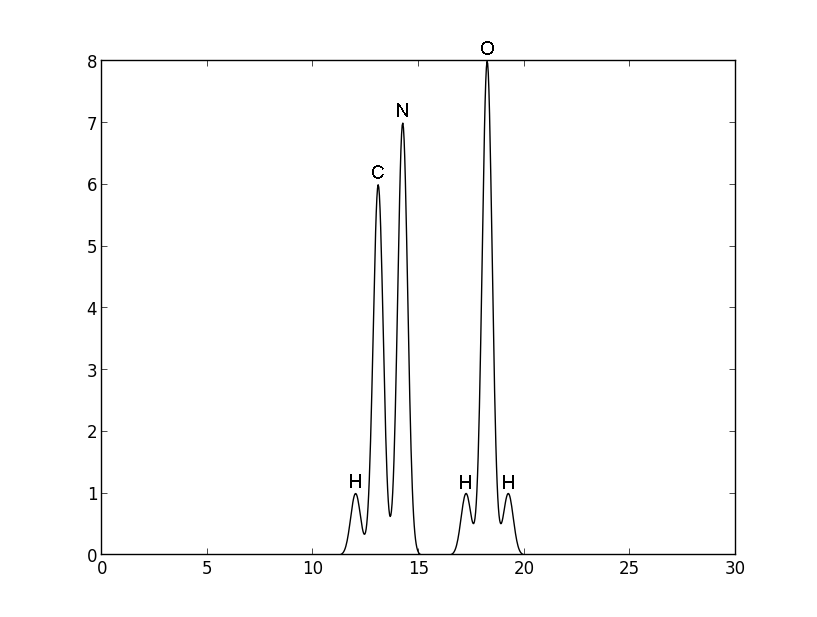
Рисунок 2. График функции электронной плотности для заданной экспериментальной модели.
Описание модельной функции ЭП полным набором гармоник
Восстановление функции ЭП с помощью разложения Фурье проводилось с помощью следующих команд, где Х — число гармоник:
python fourier-filter.py -i func_ft.txt -r 0-X -o ft_0X.txt
python fourier2func.py -f func.txt -i ft_0X.txt -o 2_func_0X.txtСамым оптимальным числом гармоник оказалось 36. Ниже представлены графики для четырёх разных чисел гармоник.
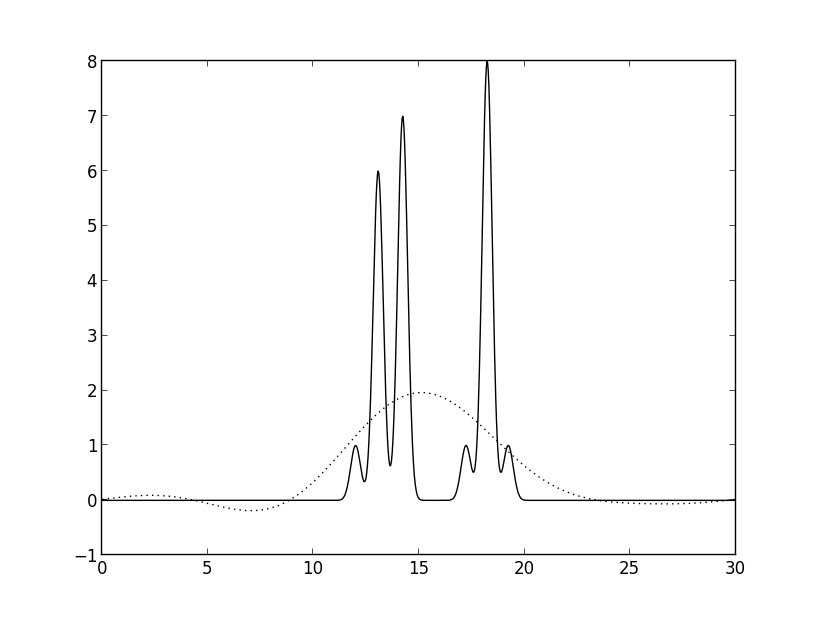 Рис. 3а. Восстановление функции ЭП 3 гармониками.
Рис. 3а. Восстановление функции ЭП 3 гармониками.
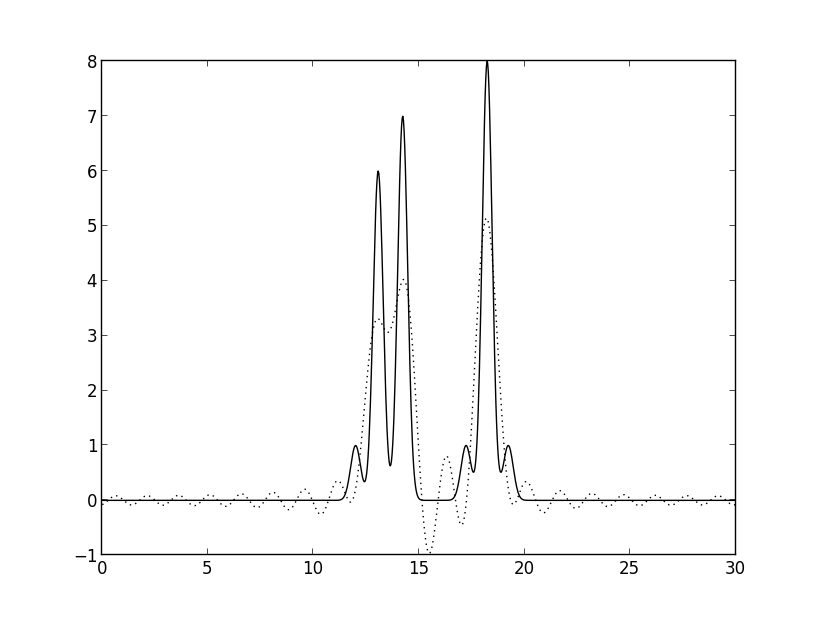 Рис. 3б. Восстановление функции ЭП 20 гармониками.
Рис. 3б. Восстановление функции ЭП 20 гармониками.
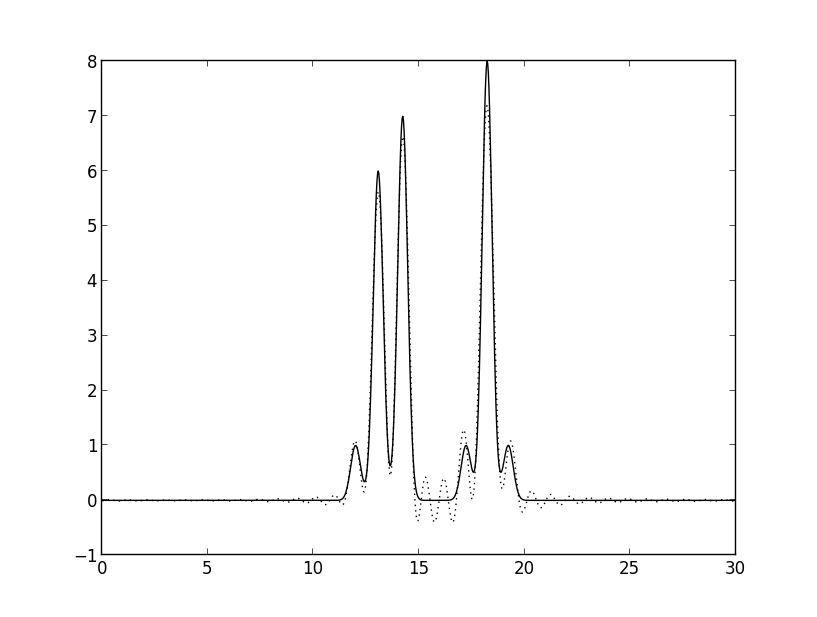 Рис. 3в. Восстановление функции ЭП 32 гармониками.
Рис. 3в. Восстановление функции ЭП 32 гармониками.
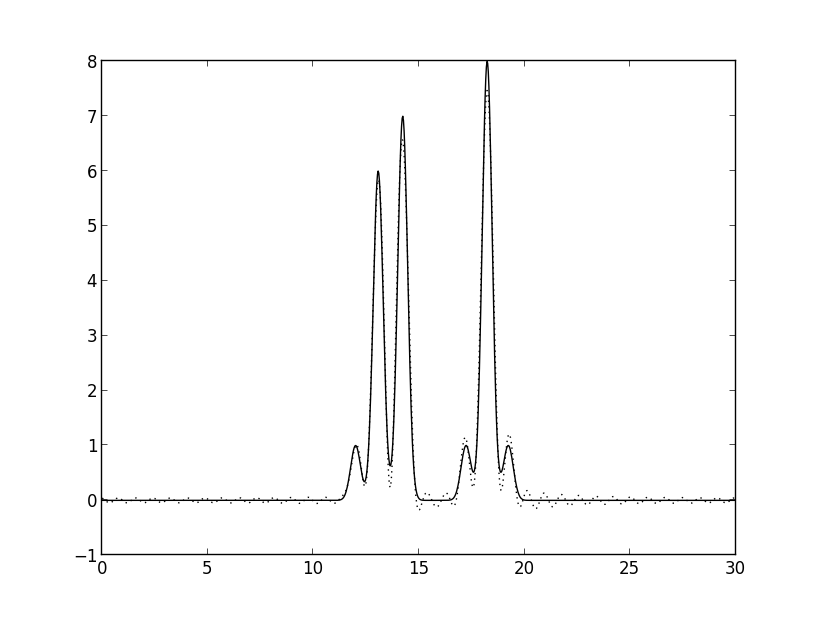 Рис. 3г. Восстановление функции ЭП 36 гармониками.
Рис. 3г. Восстановление функции ЭП 36 гармониками.
Далее к полнуму набору гармоник был добавлен шум к амплитуде или фазам (рис. 4). Ниже приведены использованные команды, где F показывает уровень шума, прибавленного к амплитуде, P — фазам:
python func2fourier.py -F 10 -P 10 -i func.txt -o noise_F10P10.txt
python fourier-filter.py -i noise_F10P10.txt -r 0-36 -o ft_F10P10_036.txt
python fourier2func.py -f func.txt -i ft_F10P10_036.txt -o 2_func_F10P10_036.txt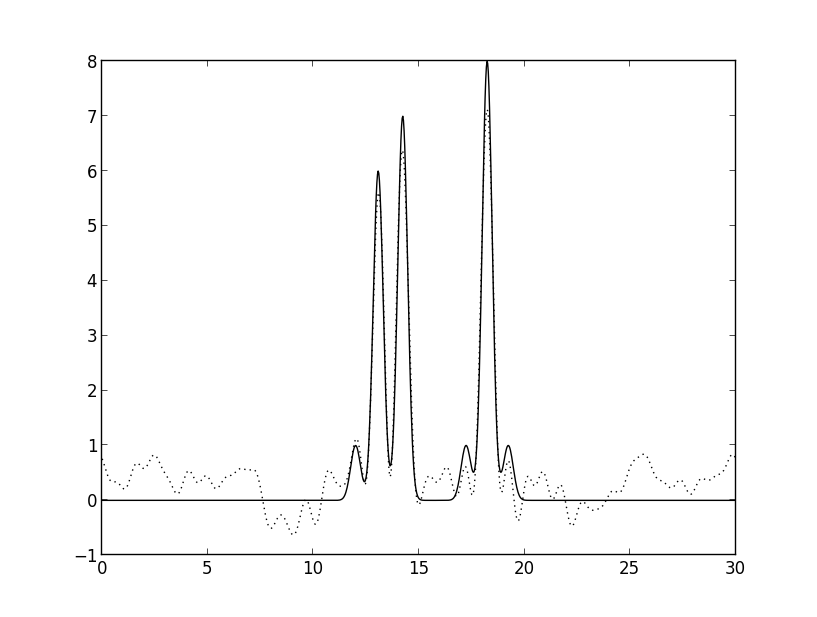 Рис. 4а. Восстановление полным набором гармоник с шумом к амплитуде, равном 30.
Рис. 4а. Восстановление полным набором гармоник с шумом к амплитуде, равном 30.
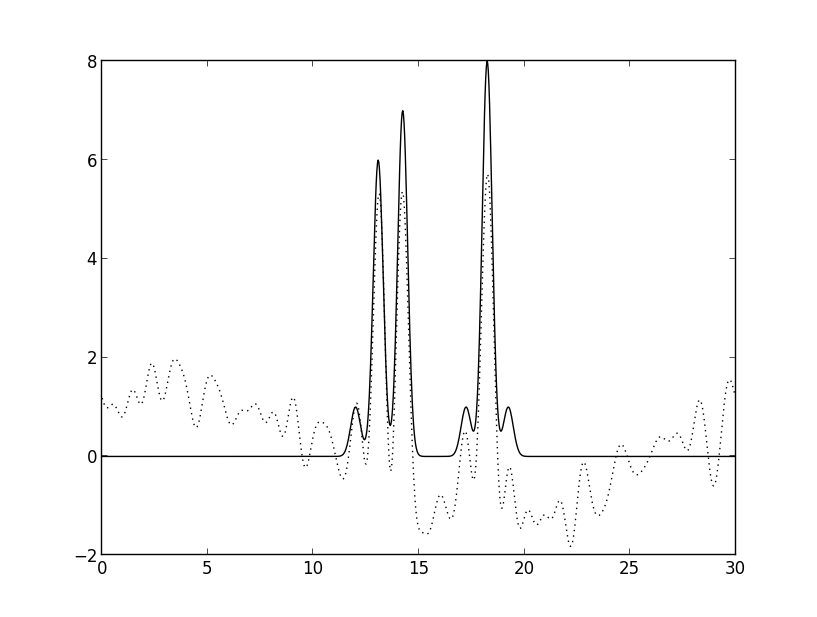 Рис. 4б. Восстановление полным набором гармоник с шумом к фазам, равном 30.
Рис. 4б. Восстановление полным набором гармоник с шумом к фазам, равном 30.
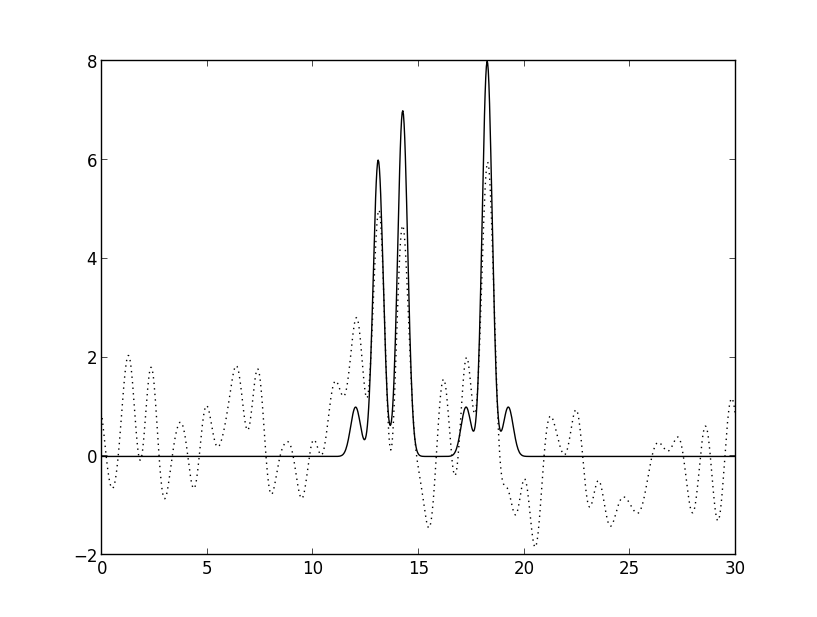 Рис. 4в. Восстановление полным набором гармоник с шумом к фазам, равном 10.
Рис. 4в. Восстановление полным набором гармоник с шумом к фазам, равном 10.
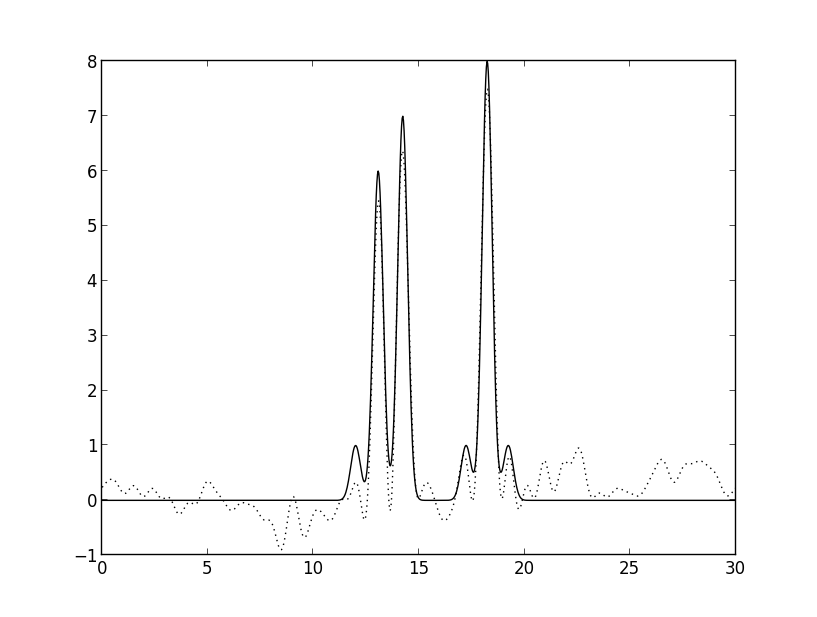 Рис. 4г. Восстановление полным набором гармоник с шумом к амплитуде и фазам, равном 10.
Рис. 4г. Восстановление полным набором гармоник с шумом к амплитуде и фазам, равном 10.
Видно, что восстановление сильно ухудшается при добавлении шума именно к фазам.
Описание модельной функции ЭП неполным набором гармоник
Помимо этого рассматривалось качество восстановления функции, если набор гармоник неполный (рис. 5а-в). Внизу представлены примерные команды:
python fourier-filter.py -i func_ft.txt -r 0-16,20-36 -o ft_036minus17-19.txt
python fourier2func.py -f func.txt -i ft_036minus17-19.txt -o 2_func_036minus17-19.txtТакже было интересно, увидеть, как на восстановление повлияет добавление быстро бьющейся гармоники (рис. 5г). Ниже находятся применённые команды.
python fourier-filter.py -i func_ft.txt -r 0-36,46 -o ft_036plus46.txt
python fourier2func.py -f func.txt -i ft_036plus46.txt -o 2_func_036plus46.txt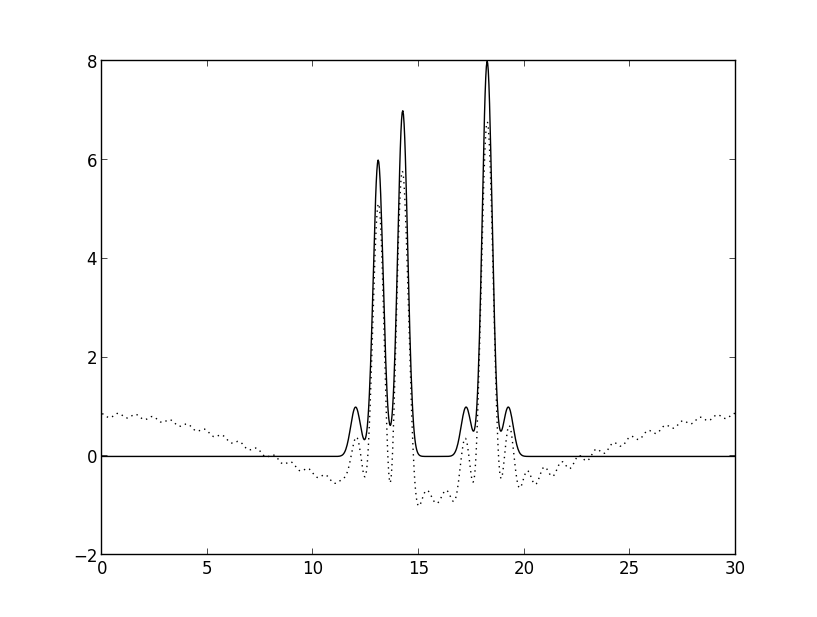 Рис. 5а. Восстановление набором гармоник без первой.
Рис. 5а. Восстановление набором гармоник без первой.
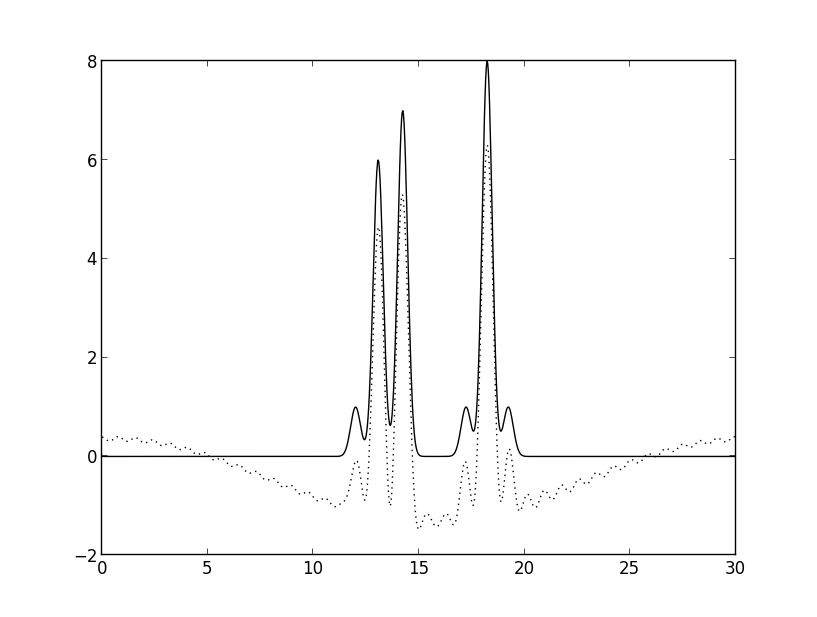 Рис. 5б. Восстановление набором гармоник без первых двух.
Рис. 5б. Восстановление набором гармоник без первых двух.
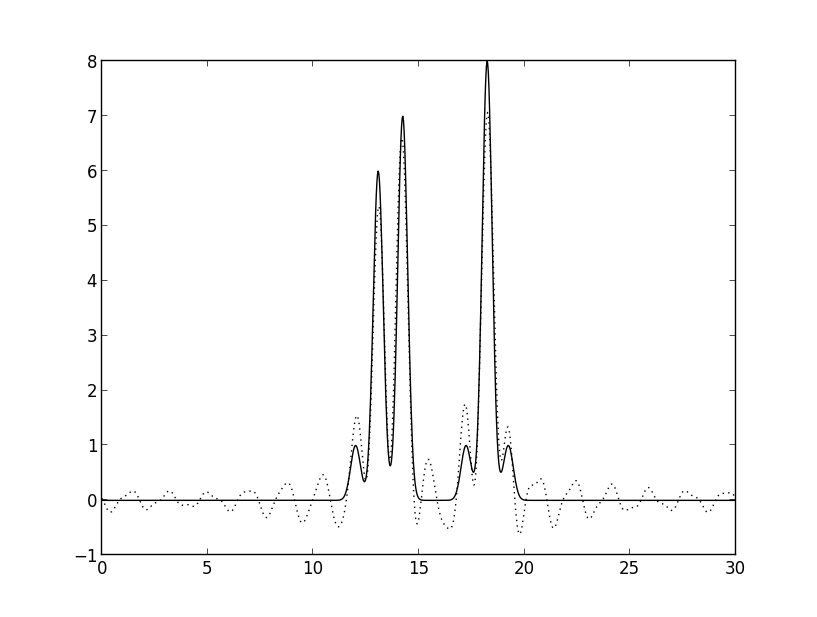 Рис. 5в. Восстановление неполным набором гармоник (нет 3 средних).
Рис. 5в. Восстановление неполным набором гармоник (нет 3 средних).
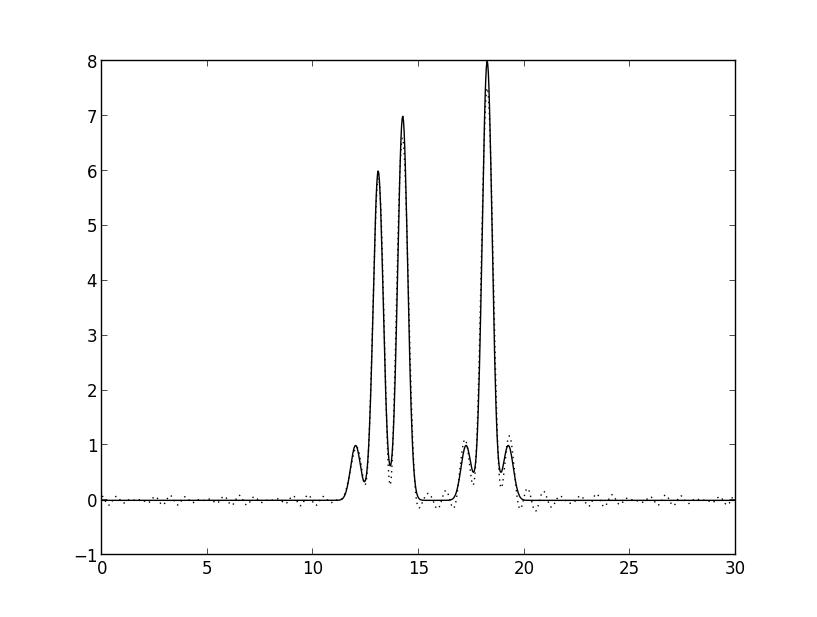 Рис. 5г. Восстановление набором из 36 гармоник с добавленной 46ой.
Рис. 5г. Восстановление набором из 36 гармоник с добавленной 46ой.
Оказалось, что более всего на качество влияло удаление средних гармоник. Добавление большой гармоники особо не повлияло на внешний вид функции.
В таблице 1 сведена полученная информация. Главным отличаем между полным и неполным набором гармоник является характеристика полноты данных. Фактически это отношение померенных гармоник к теоритически возможному числу. Например, при добавлении 46-ой гармоники мы считаем, что могли бы получить 46 гармоник, а в итоге померили только 37 (36 основных и 46-ая). В этом случае будет также отличаться разрешение, которое является периодом гармоники с наибольшем номером (в нашем случае это 30/n, где n — номер наибольшей гармоники, 30 — длина волны гармоники).
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум амплитуды (% от величины F) | Шум фазы (% от величины φ) | Качество восстановления |
| Полный набор гармоник | |||||
| 0-3 | 10 | 100 | 0 | 0 | Плохое |
| 0-20 | 1.5 | 100 | 0 | 0 | Среднее |
| 0-32 | 0.94 | 100 | 0 | 0 | Хорошее |
| 0-36 | 0.83 | 100 | 0 | 0 | Отличное |
| 0-36 | 0.83 | 100 | 30 | 0 | Среднее |
| 0-36 | 0.83 | 100 | 0 | 30 | Плохое |
| 0-36 | 0.83 | 100 | 0 | 10 | Плохое |
| 0-36 | 0.83 | 100 | 10 | 10 | Плохое |
| Неполный набор гармоник | |||||
| 1-36 | 0.83 | 97 | 0 | 0 | Отличное |
| 2-36 | 0.83 | 94 | 0 | 0 | Отличное |
| 0-16, 20-36 | 0.83 | 92 | 0 | 0 | Хорошее |
| 0-36, 46 | 0.65 | 80 | 0 | 0 | Отличное |