Сборка de novo
Объект
Собирался геном бактерии Buchnera aphidicola str. Tuc7 из одноконцевых чтений, полученных секвенированием по технологии Illumina (код доступа SRR4240356).
Подготовка чтений
Сначала были удалены чтения, содержащие адаптеры. Для этого последовательности адаптеров были собраны в один файл командой
seqret "/mnt/scratch/NGS/adapters/*" fasta::all_adapters.fastaи полученный файл был передан команде trimmomatic:
java -jar /usr/share/java/trimmomatic.jar SE -phred33 SRR4240356.fastq.gz SRR4240356_desadaptered.fastq.gz ILLUMINACLIP:all_adapters.fasta:2:7:7 &> trimmomatic_adapters.log
Из изначальных 7511529 ридов адаптерами оказались 153091 (2.04%).
После этого с конца ридов были удалены нуклеотиды качеством ниже 20, и последовательности короче 32 нуклеотидов (т.е. те, которые не дадут потом хотя бы два 31-мера) были удалены:
java -jar /usr/share/java/trimmomatic.jar SE -phred33 SRR4240356_desadaptered.fastq.gz SRR4240356_filtered.fastq.gz TRAILING:20 MINLEN:32 &> trimmomatic_filter.logИз 7358438 последовательностей, оставшихся после предыдущего шага, были удалены 305093 (4.15%)
Размер файла уменьшился с 167M до 155M после двух чисток.
Сборка
Для создания k-меров длины 31 была применена команда
velveth ./velv 31 -fastq.gz -short SRR4240356_filtered.fastq.gz &> ./velv/velveth.log
После сборка на основе этих k-меров производилась сборка:
velvetg ./velv &> velv/velvetg.log
Длины
N50 получившейся сборки равен 65554. Информация о трёх самых длинных контигах приведена в таблице 1.
| ID | lgth | out | in | short1_cov | short1_Ocov |
|---|---|---|---|---|---|
| 8 | 111962 | 0 | 1 | 38,660197 | 38,660197 |
| 6 | 107488 | 0 | 0 | 34,174029 | 34,174029 |
| 10 | 80939 | 2 | 1 | 37,524173 | 37,524173 |
Покрытие
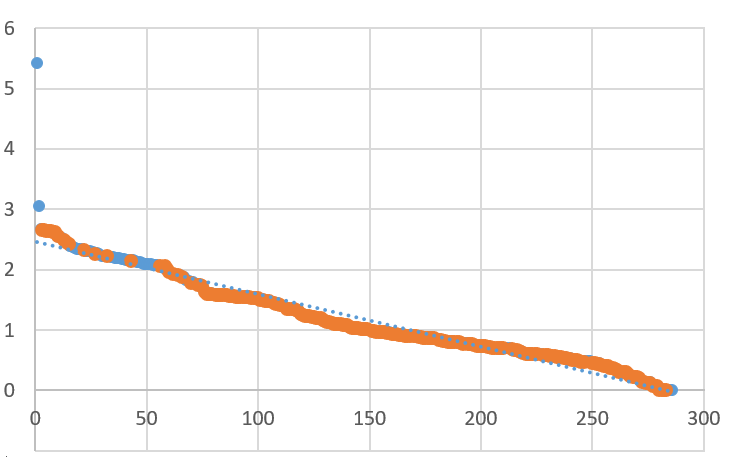
Общее распределение покрытия по контигам показано на рисунке. Видно два сильно выбивающихся значения: это контиги 64 и 127, информация о них приведена в таблице 2.
| ID | lgth | out | in | short1_cov |
|---|---|---|---|---|
| 64 | 1 | 4 | 4 | 266951 |
| 127 | 1 | 2 | 2 | 1134 |
Можно заметить, что оба эти выбивающихся контига имеют длину пути по графу равную единице, т.е. включают всего один k-мер.
Чтобы определить, что можно считать "типичной" длиной контига, я нашла среднее арифметическое и медиану для всех контигов и только для контигов с длиной пути по графу больше единицы (таблица 3). Можно видеть, что "недостоверные" контиги из одного k-мера сильно смещают среднее и практически не влияют на медиану.
| все | lgth > 1 | |
|---|---|---|
| медиана | 10,8 | 8,4 |
| среднее | 991,9 | 37,6 |
Если в качестве типичного покрытия рассматривать 10, то контигов с покрытием, отличающимся от типичного в пять и более раз получается довольно много: из 286 контигов будет 75 (26%) в большую сторону, и 21 (7%) в меньшую.
Анализ
Три самых длинных контига - 6, 8 и 10 - были выровнены с референсным геномом (AC CP009253) при помощи megablast (параметры: word size 16 (минимально возможное, чтобы была меньше вероятность "дырки"), expect threshold 0.01 (при большем слишком много "мусора" - лишних коротких выравниваний)).
Координаты по контигу ниже обозначены как n (node), по референсному геному - r (reference), на всех диаграммах контиг отложен по оси x, а референс по оси y.
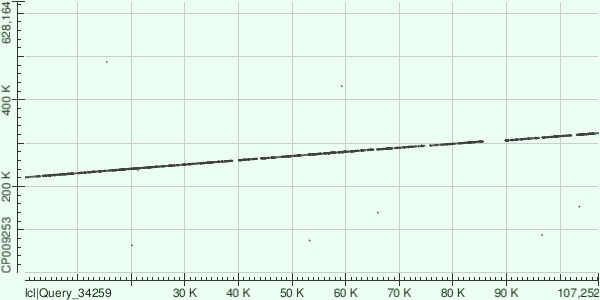
Контиг 6
Шестой контиг соответствует позициям 220869-323043 генома и разделён на 31 выравнивание (таблица 4, а также полная hit-table (примечание: серым в таблице по ссылке выравнивания небольших фрагментов контига вдали от остальных - отдельные точки вне основной линии на диаграмме).
| % identity | gap beginings | start n | end n | start r | end r |
|---|---|---|---|---|---|
| 82.454 | 19 | 146 | 2996 | 220869 | 223720 |
| 76.975 | 133 | 3385 | 7496 | 224057 | 228137 |
| 84.848 | 2 | 5544 | 5609 | 226278 | 226215 |
| 77.241 | 118 | 7580 | 11516 | 228172 | 232057 |
| 75.660 | 101 | 11665 | 16194 | 232358 | 236859 |
| 75.156 | 304 | 16292 | 26990 | 236918 | 247596 |
| 83.333 | 1 | 21193 | 21239 | 237893 | 237940 |
| 73.821 | 38 | 27075 | 28129 | 247591 | 248647 |
| 77.850 | 81 | 28467 | 31669 | 248967 | 252161 |
| 82.101 | 7 | 31898 | 32568 | 252397 | 253070 |
| 73.403 | 141 | 32780 | 37082 | 253244 | 257546 |
| 71.564 | 34 | 37314 | 38873 | 257686 | 259245 |
| 77.140 | 90 | 39869 | 43440 | 260224 | 263784 |
| 75.518 | 42 | 43986 | 45702 | 264190 | 265897 |
| 78.747 | 265 | 45989 | 55468 | 266073 | 275551 |
| 75.941 | 318 | 55527 | 63756 | 275566 | 283706 |
| 76.325 | 37 | 64004 | 65113 | 283963 | 285070 |
| 76.130 | 25 | 65810 | 67144 | 285200 | 286535 |
| 72.363 | 60 | 67352 | 68735 | 286670 | 288062 |
| 77.528 | 72 | 68934 | 72299 | 288181 | 291560 |
| 80.046 | 8 | 72508 | 73375 | 291693 | 292560 |
| 78.990 | 29 | 73534 | 74856 | 292631 | 293992 |
| 80.912 | 12 | 75721 | 77247 | 294227 | 295755 |
| 76.672 | 153 | 77556 | 84909 | 295935 | 303252 |
| 76.000 | 18 | 84991 | 85682 | 303282 | 303968 |
| 75.272 | 30 | 89750 | 90378 | 305907 | 306526 |
| 77.689 | 24 | 90714 | 91708 | 306805 | 307787 |
| 76.895 | 94 | 91741 | 96052 | 307878 | 312179 |
| 77.022 | 82 | 96698 | 100006 | 312679 | 315982 |
| 74.987 | 38 | 100155 | 102105 | 316046 | 317993 |
| 73.885 | 133 | 103039 | 107252 | 318826 | 323043 |
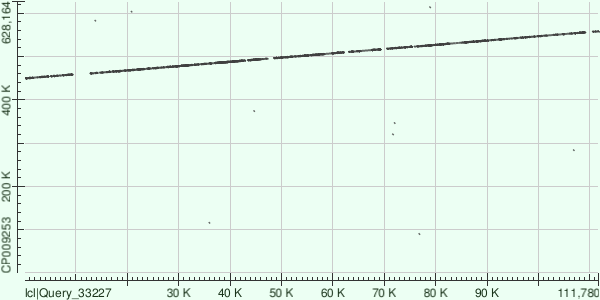
Контиг 8
Позиции 449411-558317 генома, разделён на 26 выравниваний (таблица 5, а также полная hit-table).
| % identity | gap beginings | start n | end n | start r | end r |
|---|---|---|---|---|---|
| 74.684 | 52 | 81 | 2350 | 449411 | 451656 |
| 77.089 | 46 | 2390 | 4733 | 451729 | 454069 |
| 76.697 | 78 | 5080 | 9421 | 454232 | 458568 |
| 76.913 | 14 | 12835 | 13625 | 460825 | 461613 |
| 73.378 | 12 | 13780 | 14372 | 461721 | 462315 |
| 76.989 | 135 | 14624 | 19565 | 462496 | 467421 |
| 77.030 | 170 | 19595 | 26906 | 467412 | 474667 |
| 74.193 | 209 | 27009 | 32884 | 474844 | 480660 |
| 82.216 | 18 | 33090 | 33769 | 480874 | 481545 |
| 78.328 | 4 | 33834 | 34153 | 481639 | 481960 |
| 74.078 | 241 | 34243 | 40300 | 481997 | 488106 |
| 71.905 | 121 | 40418 | 42931 | 488186 | 490673 |
| 72.036 | 101 | 43468 | 45697 | 491201 | 493457 |
| 80.130 | 13 | 45773 | 47149 | 493487 | 494864 |
| 90.000 | 4 | 47283 | 47401 | 495033 | 495148 |
| 75.295 | 120 | 48567 | 52845 | 496111 | 500325 |
| 75.618 | 265 | 52961 | 61406 | 500370 | 508806 |
| 74.261 | 19 | 61513 | 62314 | 508977 | 509769 |
| 78.553 | 140 | 63097 | 69275 | 510438 | 516539 |
| 77.208 | 79 | 70536 | 74265 | 517766 | 521500 |
| 74.954 | 33 | 74374 | 75437 | 521551 | 522614 |
| 85.671 | 1 | 75779 | 76103 | 522693 | 523020 |
| 76.851 | 159 | 76268 | 81855 | 523105 | 528679 |
| 81.465 | 399 | 81925 | 103395 | 528794 | 550219 |
| 80.859 | 102 | 103601 | 109238 | 550361 | 555905 |
| 78.182 | 15 | 110527 | 111780 | 557063 | 558317 |
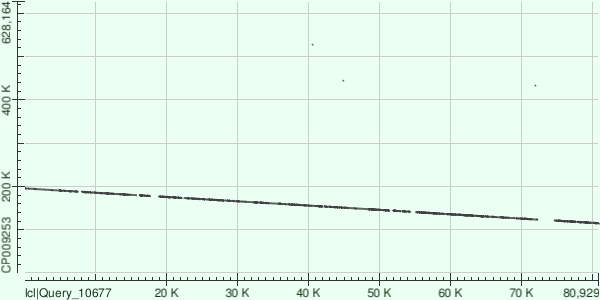
Контиг 10
Позиции 114873-195400 генома (обратная цепь), разделён на 23 выравнивания (таблица 6, а также полная hit-table).
| % identity | gap beginings | start n | end n | start r | end r |
|---|---|---|---|---|---|
| 72.675 | 123 | 77897 | 80929 | 117938 | 114873 |
| 72.700 | 130 | 74669 | 77642 | 121154 | 118219 |
| 77.466 | 16 | 71012 | 72246 | 124570 | 123332 |
| 77.011 | 52 | 69297 | 71013 | 126302 | 124604 |
| 83.736 | 9 | 67840 | 69033 | 127815 | 126623 |
| 74.890 | 430 | 55035 | 67775 | 140555 | 127825 |
| 76.050 | 34 | 53182 | 54349 | 142652 | 141477 |
| 75.280 | 46 | 51896 | 52944 | 143868 | 142826 |
| 77.800 | 178 | 43997 | 51396 | 151796 | 144368 |
| 75.028 | 39 | 42126 | 43867 | 153619 | 151886 |
| 77.684 | 191 | 33933 | 42017 | 161738 | 153752 |
| 79.601 | 89 | 28867 | 33727 | 166752 | 161898 |
| 76.185 | 138 | 22393 | 28836 | 173180 | 166750 |
| 72.500 | 5 | 21860 | 22136 | 173713 | 173436 |
| 73.336 | 95 | 18909 | 21774 | 176619 | 173750 |
| 72.241 | 60 | 16228 | 17645 | 179291 | 177865 |
| 85.005 | 1 | 14869 | 15834 | 180620 | 179654 |
| 73.608 | 38 | 13815 | 14765 | 181603 | 180661 |
| 76.002 | 82 | 10021 | 13675 | 185328 | 181712 |
| 73.782 | 62 | 8067 | 9924 | 187344 | 185497 |
| 80.046 | 73 | 2708 | 7482 | 192665 | 187938 |
| 81.307 | 4 | 1427 | 2632 | 193984 | 192777 |
| 81.944 | 11 | 37 | 1400 | 195400 | 194042 |