Практикум 3. Качество восстановления функции ЭП.
На этой странице выложен отчет по практикуму 3. Качество восстановления функции ЭП.
1. Создание модельной функции ЭП в одномерной элементарной ячейке.
Приведем условия задания.
Модель для компьютерного эксперимента. На отрезке [0,30] (ангстремы) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 ангстрем друг от друга.
Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Всего 5-7 атомов (2+3 или 2+3+2; возможны другие варианты).
Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме. Берем разные атомы.
Функция задается на интервале [0,30]. Моделируется в 1D график электронной плотности молекулы. 30 понимается как 30 ангстрем.
Функция имеет вид нескольких гауссовых кривых с центром в разных точках. Иногда - на расстоянии 1-1.5 ангстрем - модель ковалентно связанных атомов; иногда 3-5 ангстрем.
Формат файла с функцией:
#X Y [строка с # в первой колонке игнорируется]
0.0 1.01
0.01 1.07
... ....
29.97 1.00
Функцию можно создать с помощью скрипта compile-func.py. Гауссова функция определяется числами lambda,beta,gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2). Здесь a^2=a*a.
Пример задания параметров скрипта:
-g 30,3,3+40,3,4.3+2,3.5,6.5+30,3,7.5 (сумма четырех гауссовых функций: их max в точках 3,4.3,6.5,7.5, высота 30,40,2,30 соответственно; ширина "колокола" порядка 1; третий - низкий - пик
моделирует атом водорода);
ширина колокола должна примерно соответствовать диаметру атома - порядка 1 с небольшим ангстрема (электронная плотность резко спадает на таком расстоянии от центра);
высота зависит от числа электронов в атоме, поэтому может различаться.
Выл выбран вариант 3, где заданы высоты широты и координаты максимума пика. Эти данные передаются на вход скрипта compile-func.py.
Команда, заданная на вход:
python compile-func.py -g 41,3.2,24.5+21,3.7,27.5+31.0,3.2,30+10,2,10
В результате был получен файл func.txt. Также был получен графический файл. Он представлен на рисунке 1.
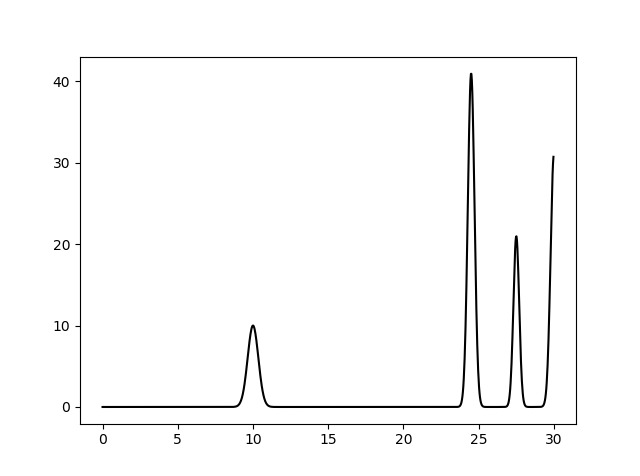
Рис. 1. Функция в графическом виде.
2. Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные.
Далее была запущена команда:
python func2fourier.py -i func.txt
В результате был получен файл func_ft.txt. Получено 498 гармоник.
3. Отбор подходящих гармоник и восстановление исходной функции ЭП по полному набору гармоник.
Для начала был запущен скрипт fourier-filter.py с помощью команды
python fourier-filter.py func_ft.txt -r 0-5
В результате был получен файл func_ft_filtered.txt.
Далее с помощью команды
python fourier2func.py func_ft_filtered.txt
результат фильтрации был визуализирован. В результате мы можем сравнить воссановленную фунцию с исходной по следующим критериям:
Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"
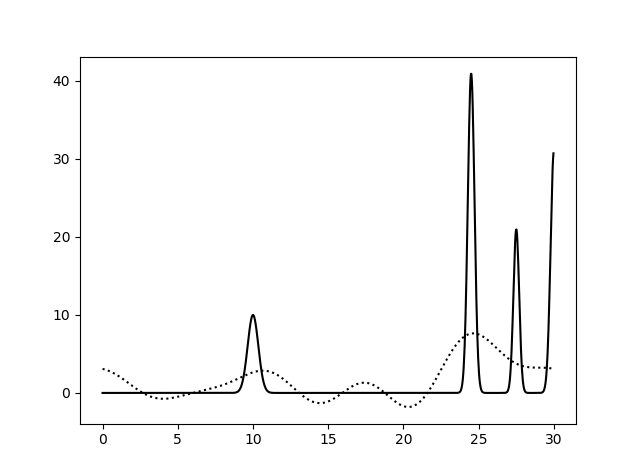
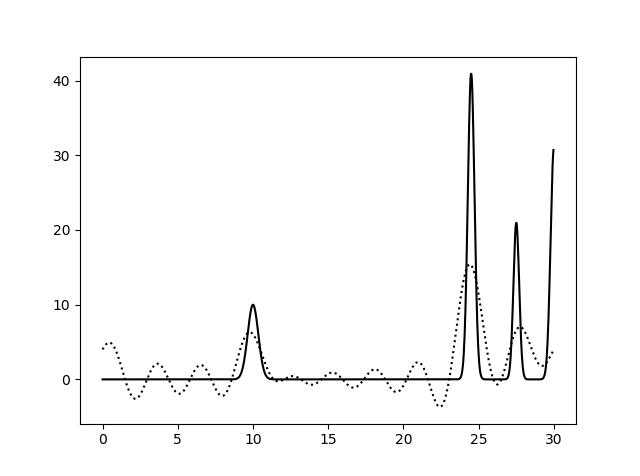
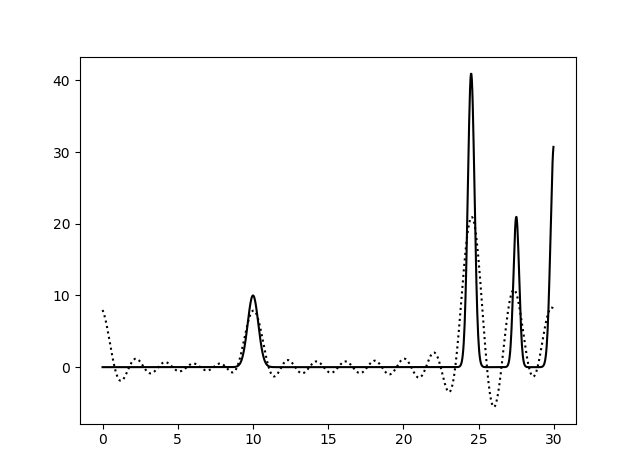
Рис. 2. Гармоники с 0 по 5, с 0 по 10 и с 0 по 15.
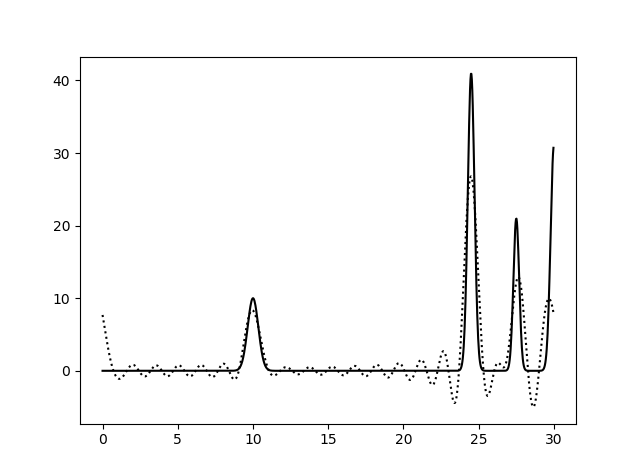
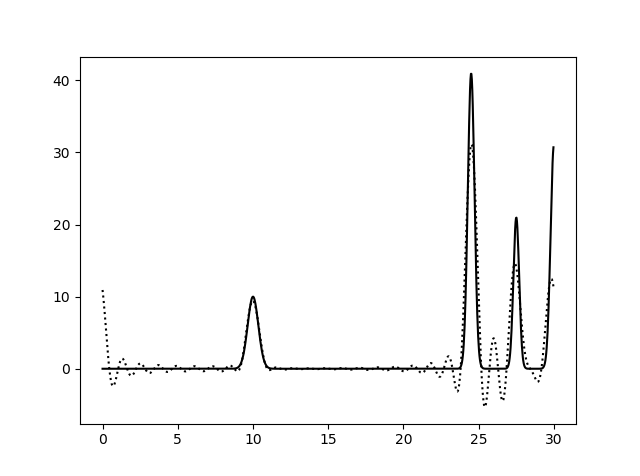
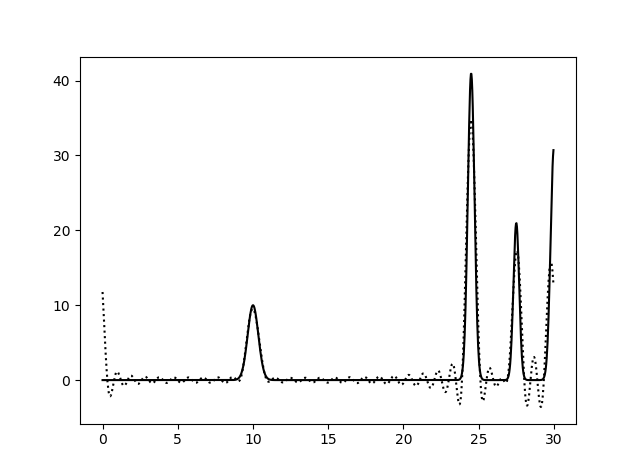
Рис. 3. Гармоники с 0 по 20, с 0 по 25 и с 0 по 30.
Соответственно выше представлены наборы гармоник с 0 по 5, с 0 по 10, с 0 по 15, с 0 по 20, с 0 по 25, с 0 по 30. Сплошная линия - это график исходной функции, пунктирная -
график восстановленной. Можно сделать вывод, что для восстановления функции достаточно гармоник с 0 по 25.
4. Восстановление исходной функции при наличии гауссова шума.
Для того, чтобы модель стала более реальной мы добавляем гауссовский шум. Шум добавляем по амплитуде(-F) и по фазе(-P).
Использована команда:
python func2fourier.py func.txt -F 20 -P 20
python fourier-filter.py func_ft.txt -r 0-25
python fourier2func.py func_ft_filtered.txt
Полученные визуализации, представлены ниже.
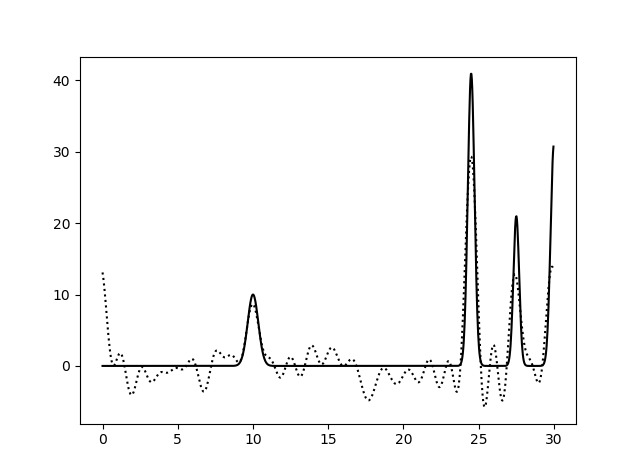
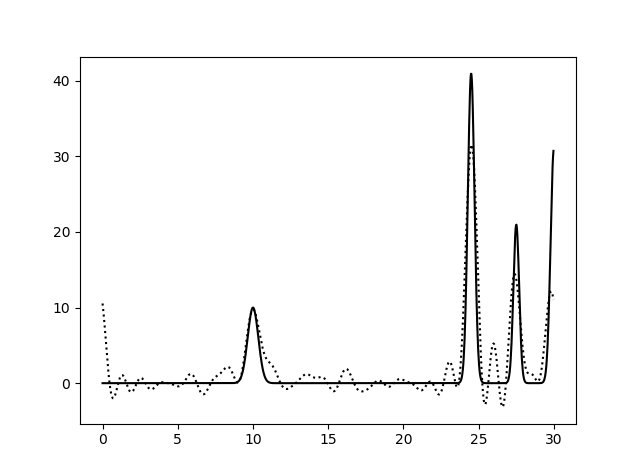
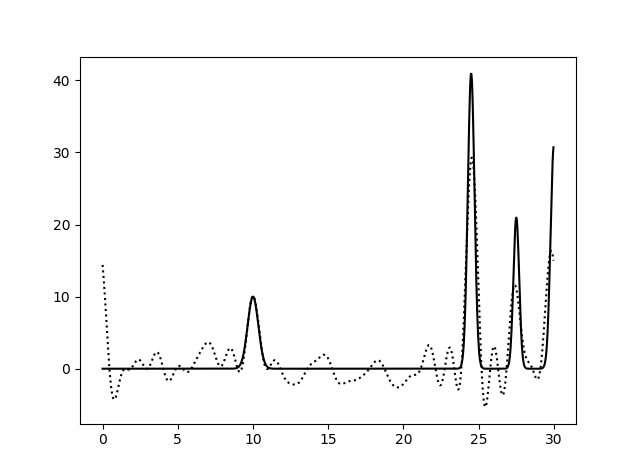
Рис. 4. Гармоника с F = 20, P = 20, гармоника с F = 20, P = 0, гармоника с F = 0, P = 20.
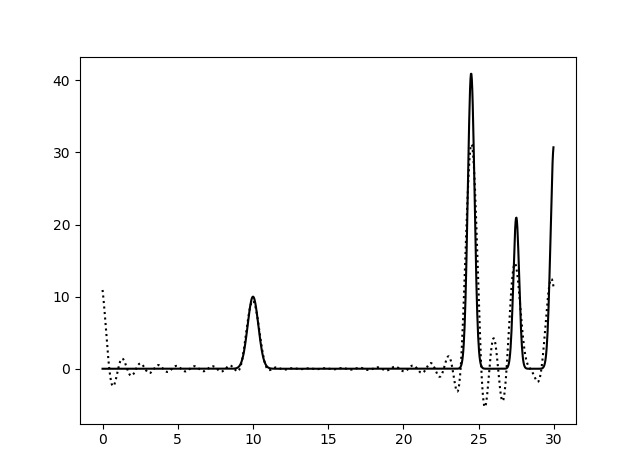
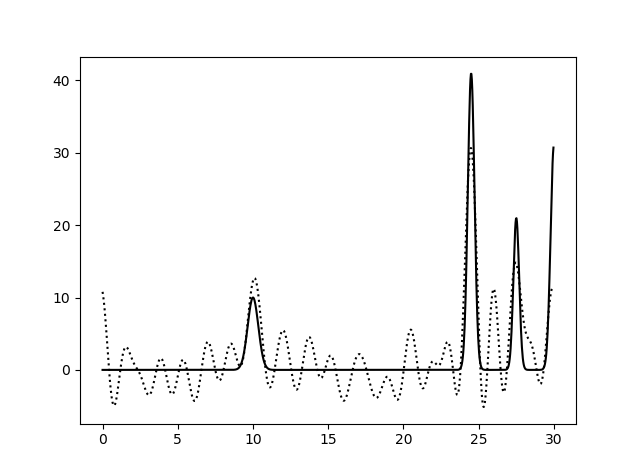

Рис. 5. Гармоника с F = 0, P = 0, гармоника с F = 60, P = 0, гармоника с F = 0, P = 60.
Можно сделать вывод(из второй и третьей картинок), что наличие шумов по фазе больше снижает качество восстановления, чем присутствие шумов по амплитуде.
5. Восстановление исходной функции при неполном наборе гармоник.
Теперь рассмотрим как может быть восстановлена функция при неполном наборе гармоник. Это важно, поскольку не всегда в реальности можно получить полный набор гармоник.
Для этого запустим следующие команды:
python func2fourier.py func.txt
python fourier-filter.py func_ft.txt -r 0-10,15-25
python fourier2func.py func_ft_filtered.txt
С помощью этих команд были поочередно удалены команды с самым маленьким(с 0 по 10), средним(с 10 по 15) и самым большим(с 15 по 25).
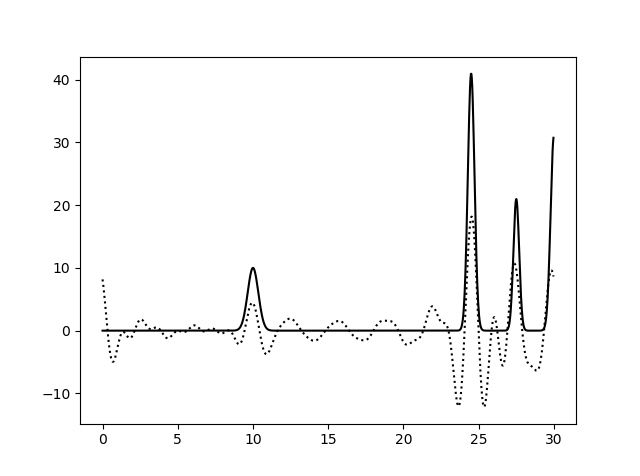
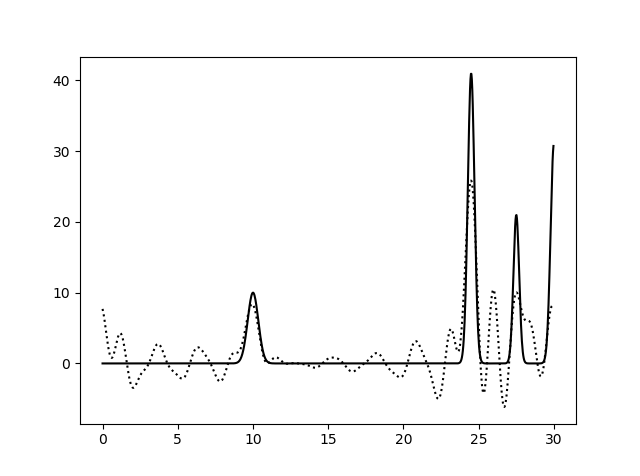
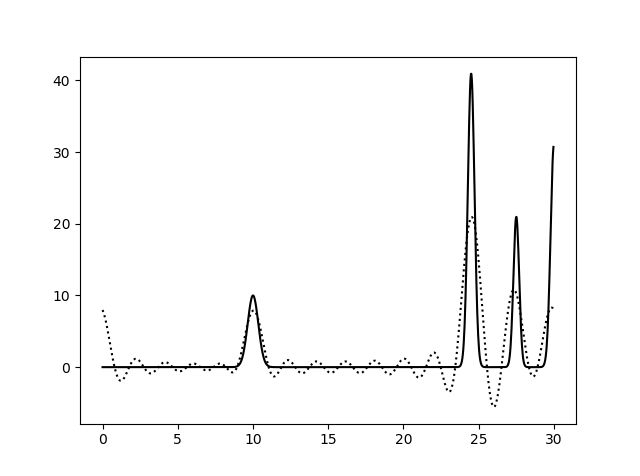
Рис. 6. Гармоника от 10 до 25, гармоника 0-10, 15-25, гармоника от 0 до 15.
Можно увидеть, что хуже всего выглядят картинки, с удаленными центральными гармониками. Лучше всего восстановлена функция от 0 до 15.
Гармоники с маленьким разрешением нужны, чтобы функция была нормально восстановлена.
6. Итог.
| Набор гармоник | Разрешение(А) | Полнота(%) | Шум амплитуд(%) | Шум фаз(%) | Качество разрешения | Дополнение |
| Полный набор гармоник |
| Набор гармоник | Разрешение(А) | Полнота(%) | Шум амплитуд(%) | Шум фаз(%) | Качество разрешения | Дополнение |
| 0-5 | 6 | 100 | 0 | 0 | Плохое | |
| 0-10 | 3 | 100 | 0 | 0 | Хорошее | |
| 0-15 | 2 | 100 | 0 | 0 | Отличное | |
| 0-20 | 1.5 | 100 | 0 | 0 | Отличное | |
| 0-25 | 1.2 | 100 | 0 | 0 | Отличное | Оптимальное количество гармоник |
| 0-30 | 1 | 100 | 0 | 0 | Отличное | Очень хорошее разрешение, почти идеальное |
| Полный набор гармоник при наличии гауссовского шума |
| 0-25 | 1.2 | 100 | 20 | 20 | Хорошее | Есть много шума, но пики определяются довольно четко |
| 0-25 | 1.2 | 100 | 20 | 0 | Отличное | Шум практически не мешает определить максимумы |
| 0-25 | 1.2 | 100 | 0 | 20 | Среднее | Некоторые пики, даваемые шумом неотличимы от максимумов |
| 0-25 | 1.2 | 100 | 0 | 0 | Отличное | Максимумы оппределяются, но восстановленная функция не до конца совпадает с исходной |
| 0-25 | 1.2 | 100 | 60 | 0 | Среднее | Некоторые пики, даваемые шумом неоличимы от максимумов функции |
| 0-25 | 1.2 | 100 | 0 | 60 | Плохое | Шум дает график, практически не имеющий ничего общего с исходной функцией |
| Неполный набор гармоник |
| 10-25 | 2 | 60 | 0 | 0 | Хорошее | Пики в целом угадываются, но есть неправильные пики, можно определить положение некоторых атомов |
| 0-10, 15-25 | 1.5 | 80 | 0 | 0 | Хорошее | Очертания функции верные, положение амов можно определить, зная количество атомов |
| 0-15 | 2 | 60 | 0 | 0 | Отличное | Очертания функции верные, практически точно совпадают с исходной функцией |
Ссылки:
[1] Hodge T. & Cope M.J.T.V. 2000. A myosin family tree. Journal of Cell Science 113:3353-3354.
[2] Briggs G.S., Smits W.K., Soultanas P. (2012). Chromosomal Replication Initiation Machinery of Low-G+C-Content Firmicutes. J Bacteriol. 194, 5162-70.
[3] Semova, I., Carten, J.D., Stombaugh, J., Mackey, L.C., Knight, R., Farber, S.A., and Rawls, J.F. (2012). Microbiota Regulate Intestinal Absorption and Metabolism of Fatty Acids in the Zebrafish. Cell Host Microbe 12, 277-288.
[4] Backhed, F., Ding, H., Wang, T., Hooper, L.V., Koh, G.Y., Nagy, A., Semenkovich, C.F., and Gordon, J.I. (2004). The gut microbiota as an environmental factor that regulates fat storage. Proc. Natl. Acad. Sci. USA 101, 15718–15723.















