Отчет по практическому занятию №12

Эволюционные расстояния между последовательностями

• оценка доли несовпадающих нуклеотидов;
• метод Джукса-Кантора.

Теперь предположим, что этой информации у нас нет, и оценим расстояние между последовательностями с помощью двух обозначенных выше методов. При этом нужно вычислять расстояния между всеми возможными парами последовательностей, так как мы не можем знать, какая из них является предковой.

Уточню соответствия названий последовательностей, которые будут встречаться в таблицах далее, указанным на дереве элементам. Листья сохраняют те же названия, а все узлы, а также корень, получают названия соответственно Seq1, Seq2, Seq3, Seq4 и Seq5.

Подсчет реальных эволюционных расстояний для каждой пары последовательностей был осуществлен с использованием приведенного выше дерева. В результате я получила следующую матрицу:

Истинные расстояния в моей выборке (число замен на 100 нуклеотидов)

Программа distmat предназначена для подсчета расстояний между последовательностями во множественном выравнивании. Поскольку гэпов при точечных заменах нуклеотидов мы получить не могли, можно не использовать программу emma для построения выравнивания, а просто поместить все последовательности в один файл одну под другой. При разных значениях параметра -nucmethod программа distmat позволяет получить как матрицу для среднего числа несовпадающих нуклеотидов (в расчете на 100 нуклеотидов), так и для посчитанных по методу Джукса-Кантора попарных эволюционных расстояний. Параметр -nucmetod 0 используется в первом случае, а параметр -nucmethod 1 — во втором.

Матрица попарных различий (среднее число несовпадающих нуклеотидов на 100 нуклеотидов)	Матрица попарных расстояний (метод Джукса-Кантора)
Seq1 Seq2 Seq3 Seq4 Seq5 A B C D E F Seq1 0 Seq2 22 0 Seq3 26 39 0 Seq4 30 43 7 0 Seq5 41 50 20 25 0 A 47 34 56 58 61 0 B 47 35 57 58 62 54 0 C 47 54 33 29 44 68 63 0 D 46 53 36 30 44 63 61 46 0 E 51 58 35 38 20 66 66 53 53 0 F 51 57 35 39 19 67 67 51 53 33 0	Seq1 Seq2 Seq3 Seq4 Seq5 A B C D E F Seq1 0 Seq2 26 0 Seq3 32 55 0 Seq4 39 65 7 0 Seq5 60 83 23 30 0 A 74 46 102 111 127 0 B 74 47 105 112 133 95 0 C 75 95 44 36 65 174 137 0 D 70 93 48 39 65 140 123 72 0 E 86 112 46 53 23 158 158 91 91 0 F 86 108 47 55 22 163 163 86 91 44 0

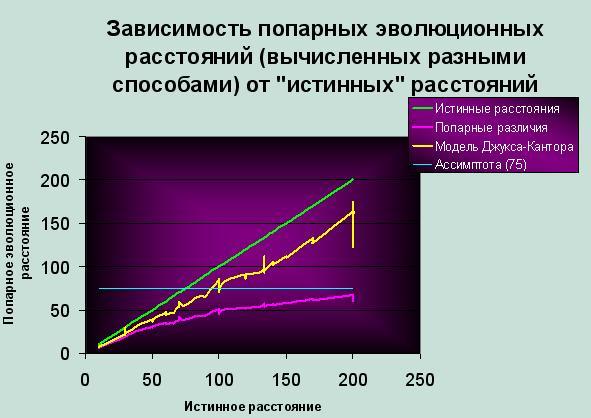
Теперь с помощью Excel можно просто составить из этих трех матриц одну отсортированную по убыванию истинных расстояний таблицу, в которой для каждой из возможных пар последовательностей указано истинное расстояние и два посчитанных программой distmat расстояния. Построенный по этой таблице график приведен ниже.

Как можно видеть по этому графику, модель Джукса-Кантора лучше высчитывает истинное расстояние между последовательностями, нежели простой подсчет несовпадений нуклеотидов. При малых расстояниях между последовательностями обе модели дают хорошо согласующиеся с истинными данными цифры. Границы применимости модели Джукса-Кантора шире, чем при использовании числа попарных различий, и это график отражает особенно ярко. Мы видим, что при большом значении истинного расстояния между последовательностями процент несовпадений стремится к 75% — т.е. к проценту несовпадения двух случайных нуклеотидных последовательностей, поэтому, разумеется, перестает отражать истинную суть процесса дивергенции последовательностей. Обе модели предсказывают меньшее попарное расстояние между последовательностями, чем оно есть на самом деле.