Отчет по практическому занятию №11

Часть I — работа с исходным деревом

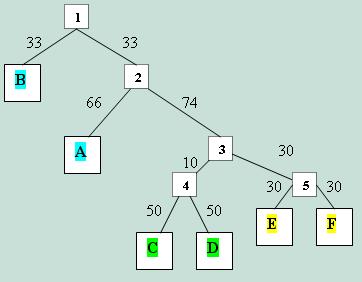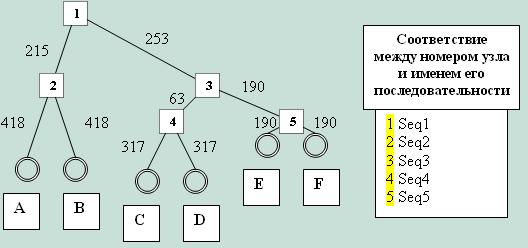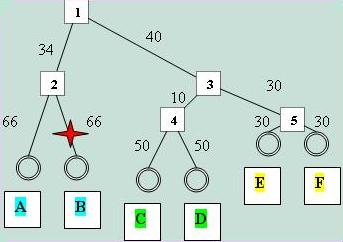
Восстановим изображение дерева по его скобочной формуле (которая была дана): ((А:66,В:66):34,((С:50,D:50):10,(Е:30,F:30):30):40); Полученная картинка с указанием длин ветвей как числа замен на 100 нуклеотидов приведена ниже. Звездочка показывает положение нового корня в дереве "Модель B"; его топография описывается в задании №5. 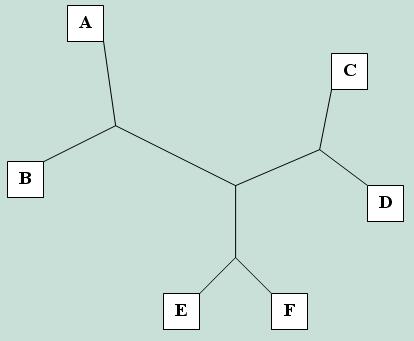В ультраметрическом дереве расстояния от всех листьев до корня должны быть одинаковы, и мое дерево, как легко убедиться, удовлетворяет этому условию: 66+34 = 50+10+40 = 30+30+40 = 100 Если считать это дерево бескорневым, то его ветви как различные разбиения множества листьев на две части можно представить следующим образом: 2-3 {A,B} | {C,D,E,F} 3-4 {C,D} | {A,B,E,F} 3-5 {E,F} | {A,B,C,D}

Другие варианты изображения этого же дерева приведены ниже:

              +----------------A
              |
   +----------|
   |	      +----------------B
   |
---|                    +------C
   |                    |
   |                    |
   |          +---------|
   |          |         |
   |          |         +------D
   |          |
   +----------|
              |         +------E
              |         |
              |         |
              +---------|
                        |
                        |
                        +------F

Переукоренение дерева

Если переместить корень в положение, отмеченное на первом реконструированном изображении моего дерева звездочкой, то полученное дерево можно будет представить в виде, показанном на рисунке слева. Очевидно, что полученное дерево не будет ультраметрическим: расстояние от листа B до корня меньше расстояния от корня до любого другого листа. Описание ветвей дерева как множества разбиений листьев будет таким же, как и для модели A, так как при таком описании мы не смотрим на положение укоренения.

+---B | | ---| +-----C | +------A | | | | | | +-| +---| | | | | +-----D | | +-------| | +---E | | +---| | | +---F

Прямоугольная филограмма для модели B будет иметь следующий вид (одной черточкой отображено число мутаций ~ 10 на 100 нуклеотидов) Скобочная формула нового дерева будет такой: (B:33, (A:66,((C:50,D:50):10,(E:30,F:30):30)):74):33)

Часть II — получение мутантных последовательностей

Длина гена белка CRP_ECOLI — 633 нуклеотидных остатка. Пересчет числа мутаций, которые необходимо провести в последовательности гена белка CRP_ECOLI, позволяет выписать новые длины ветвей дерева, представляющего собой модель эволюции этого гена. В качестве последовательности 1 возьмем последовательность гена белка CRP_ECOLI и далее будем производить случайные мутации в ней с помощью программы msbar. В качестве параметров программы мы используем -point и -auto. Параметр -point 4 задает программе тип точечных мутаций, которые она должна совершать: в данном случае, это замены (changes). Параметр -auto устанавливает остальные параметры мутаций (т.е. мутации блоков и кодонов) по умолчанию без уведомления об этом пользователя. Их значение по умолчанию — 0, т.е. в нашем случае такие мутации запрещены.

Текст скрипта

msbar Seq1.fasta Seq2.fasta -point 4 -count 215 -auto
msbar Seq1.fasta Seq3.fasta -point 4 -count 253 -auto

msbar Seq2.fasta A.fasta -point 4 -count 418 -auto
msbar Seq2.fasta B.fasta -point 4 -count 418 -auto

msbar Seq3.fasta 4.fasta -point 4 -count 63 -auto
msbar Seq3.fasta 5.fasta -point 4 -count 190 -auto

msbar Seq4.fasta C.fasta -point 4 -count 317 -auto
msbar Seq4.fasta D.fasta -point 4 -count 317 -auto

msbar Seq5.fasta E.fasta -point 4 -count 190 -auto
msbar Seq5.fasta F.fasta -point 4 -count 190 -auto