
|
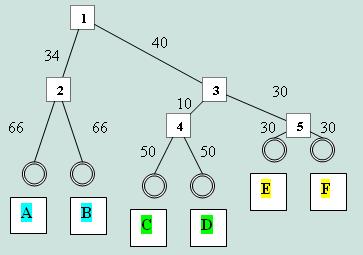
A 0.0000 0.9501 1.7385 1.3966 1.5800 1.6338 B 0.9501 0.0000 1.3667 1.2328 1.5800 1.6338 C 1.7385 1.3667 0.0000 0.7243 0.9065 0.8554 D 1.3966 1.2328 0.7243 0.0000 0.9065 0.9119 E 1.5800 1.5800 0.9065 0.9065 0.0000 0.4437 F 1.6338 1.6338 0.8554 0.9119 0.4437 0.0000 |
Во всех программах параметры устанавливались по умолчанию, за исключением программы ednaml, которая учитывает отношение числа транзиций к числу трансверсий. Оно по объясненным выше причинам равно 1 в рамках нашей модели.
+----------------------------A
+----------------4
! +----------------------------B
!
--5 +---------------------C
! +----2
! ! +---------------------D
+------------------3
! +-------------E
+------------1
+-------------F
|
UGPMAЕдинственное укорененое дерево, и единственное, полностью совпавшее по топологии с исходным. Алгоритм UGPMA является эвристическим, а не переборным, и работает на основании матрицы расстояний, а не множественного выравнивания. Скобочная формула дерева —((A:0.47505,B:0.47505):0.28509,((C:0.36215,D:0.36215):0.08539, (E:0.22185,F:0.22185):0.22569):0.31260); |
+-----------C
!
! +------E
--4--------2
! +------F
!
! +---------------A
! +----------------1
+--3 +-----------B
!
+--------D
|
Neighbor–JoiningЭвристический алгоритм, осуществляемый программой eneighbor, является в каком-то смысле "обратным" к UGPMA; он не строит дерево от листьев к предковым последовательностям, в конечном итоге — корню, а разрешает изначально созданную небинарность. Разумеется, в ходе такого алгоритма дерево не может стать укорененным.Скобочная формула дерева — (C:0.38068,(E:0.22050,F:0.22320):0.27842,((A:0.54200,B:0.40810):0.56380, D:0.27585):0.10042); |
+-------------B ! ! +-------D ! ! --1------------------2 +------F ! ! +---------4 ! +---3 +-------E ! ! ! +----------C ! +---------------A |
Maximum LikelihoodСкобочная формула дерева —(B:0.45513,(D:0.25697,((F:0.20970,E:0.24356):0.31320, C:0.36593):0.14366):0.61341,A:0.52233); |
+--------D
!
+--3 +--F
! ! +--5
! +--4 +--E
+--2 !
! ! +-----C
--1 !
! +-----------B
!
+--------------A
|
Maximum ParsimonyКак легко видеть из скобочной формулы полученного этим переборным алгоритмом дерева, он не измеряет длины ветвей. Является символьно-ориентированным.Скобочная формула дерева — (((D,((F,E),C)),B),A); |
| ABCDEF | Исходное дерево модели | UGPMA | NJ | ML | Parsimony |
| **0000 | + | + | + | + | + |
| 00**00 | + | + | - | - | - |
| 0000** | + | + | + | + | + |
| **0*00 | - | - | + | + | + |
Два других метода являются символьно-ориентированными, и на примере выравнивания было бы сложнее отразить то же, что показывает матрица расстояний. Кроме того, об алгоритме их работы я знаю меньше, поэтому я не смогла предположить возможных причин получения именно таких данных. Однако то, что эти методы воссоздали точно такое же дерево, косвенно указывает на возможную справедливость моей теории.
© Dibrova Dasha aka UdavDasha, 2005 |