Практикум 13
Сравнение выравнивания одних и тех же последовательностей разными программами
Для выполнения данного практикума было выбрано семейство доменов эукариотической аспартиловой протеазы(Eukaryotic aspartyl protease- Asp, PF00026). Это семейство включает пепсины, катепсины и ренины. Я выбрала семейство Asp так как оно содержит всего 24 последовательности, причем они длинные, в среднем 284,2 аминокислоты, то есть будет хороша видна разница в выравниваниях, но при этом сравнивать будет удобно.
Сравнение с использованием VerAlign
В Jalview я загрузила из PFAM домены эукариотической аспартиловой протеазы и выравняла их тремя разными программами - MAFFT, MUSCLE, T-Coffee. Были выбраны именно эти программы, так как они дают лучшие результаты среди доступных в Jalview. Референсным будем считать выравнивание с помощью MAFFT.
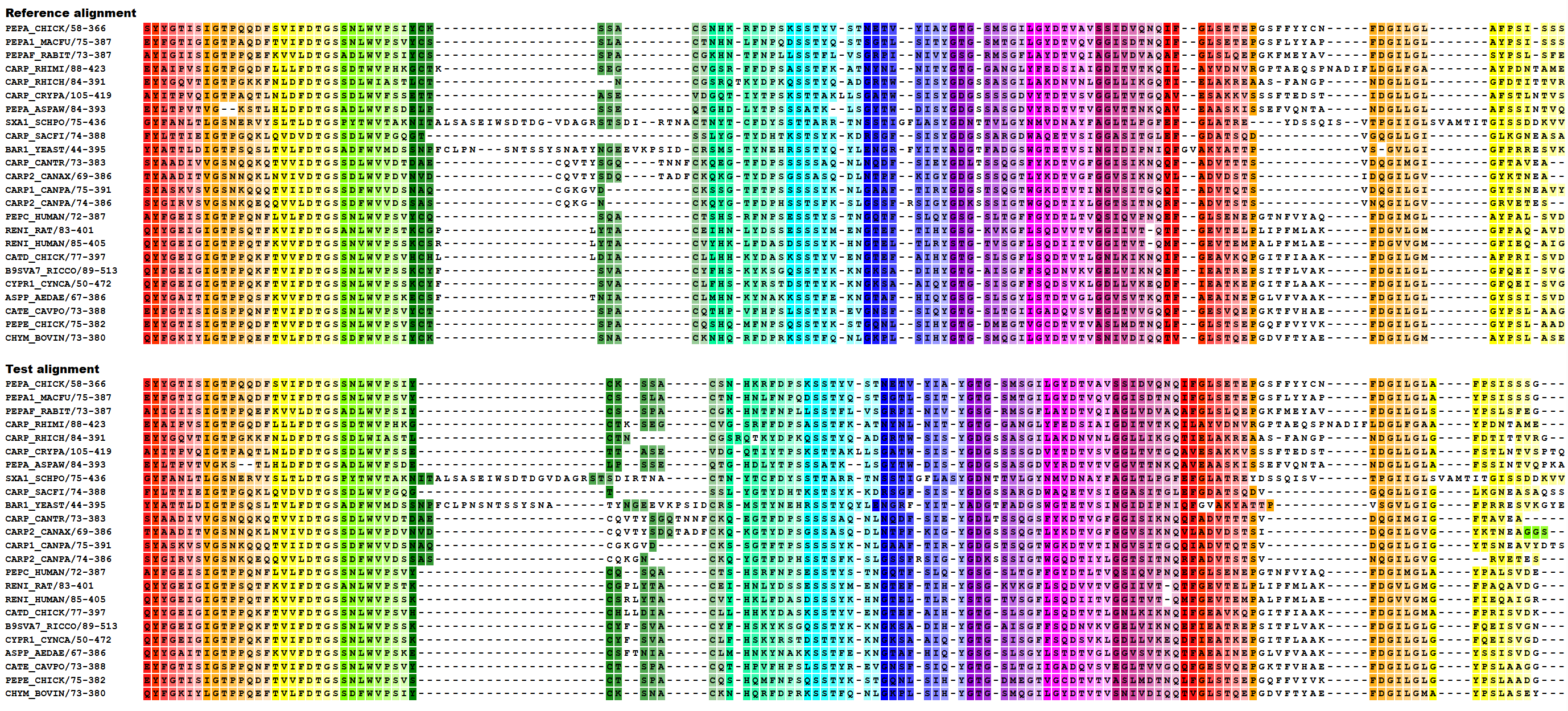
На изображении ниже Reference alignment - выравнивание MAFFT, Test alignment - выравнивание MUSCLE. Примеры одинаково выравненных блоков: (14,32)=(14,32) длины 19; (65,67)=(67,69) длины 3; (71,80)=(73,82) длины 10; (99, 117)=(101,119) длины 19. Примеры неодинаково выравненных блоков: (33,64)-(33,66); (68,70)-(70,72); (122,145)-(124,145).
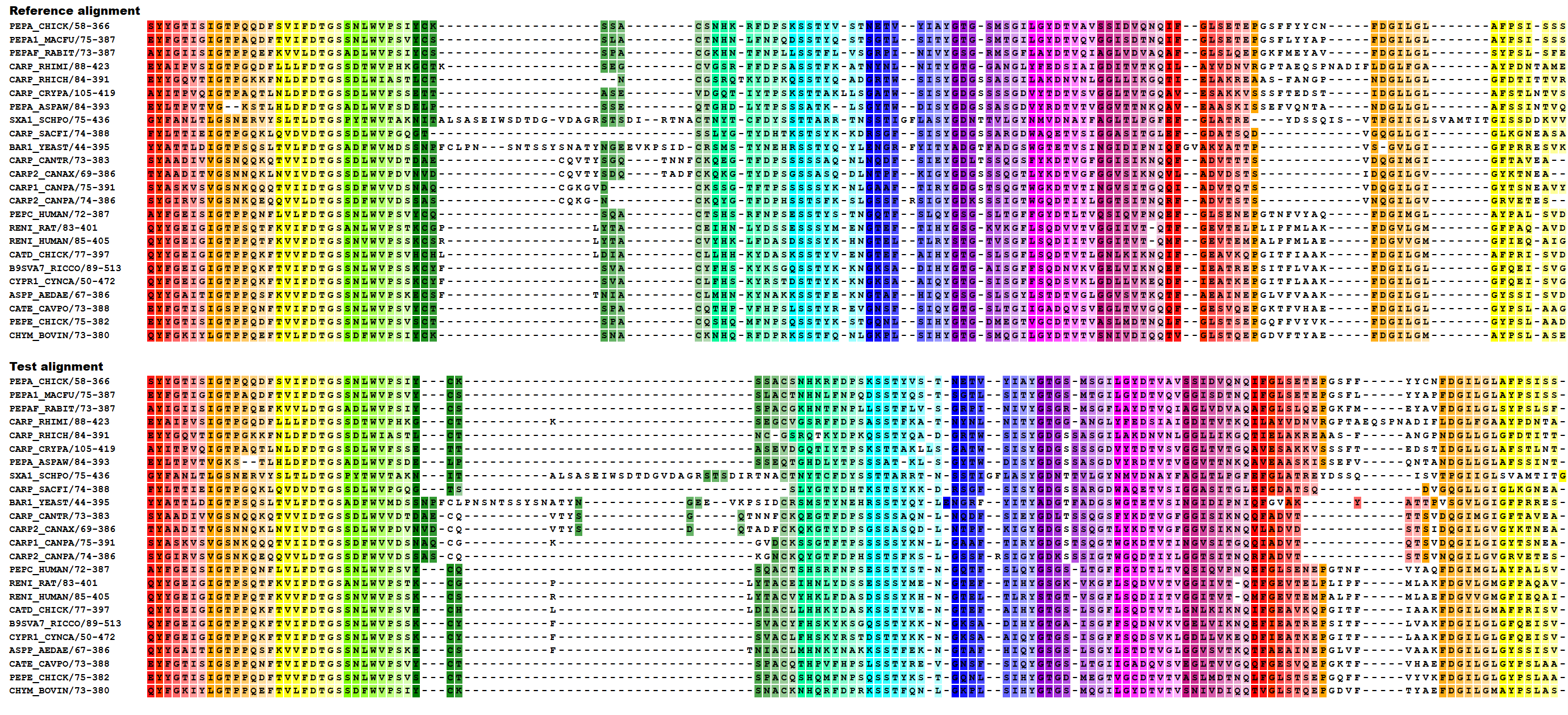
Далее с MAFFT я сравнила выравнивание T-Coffee. Одинаково выравненные блоки:(14,32)=(14,32) длины 19; (71,79)=(80,88) длины 8; (91,97)=(101,107) длины 6. Неодинаково:(33,70)-(33,79); (80,90)-(89,100); (124,145)-(132,153).
Ссылка на выравнивания: Проект в Jalview
Сравнение с использованием программы Мити Липченчука
Программа была вызвана с опциями -b и -o, позволюящими выводить координаты блоков без гэпов.
Первая таблица с одинаковыми блоками в двух выравниваниях
| MAFFT | MUSCLE |
| 1 - 9 | 1 - 9 |
| 14 - 32 | 14 - 32 |
| 65 - 67 | 67 - 69 |
| 71 - 80 | 73 - 82 |
| 94 - 97 | 96 - 99 |
| 99 - 117 | 101 - 119 |
| 119 - 121 | 121 - 123 |
| 146 - 150 | 146 - 150 |
| 190 - 199 | 189 - 198 |
| 211 - 232 | 210 - 231 |
| 248 - 259 | 247 - 258 |
| 284 - 301 | 283 - 300 |
| 426 - 428 | 427 - 429 |
| 452 - 458 | 452 - 458 |
| 475 - 480 | 475 - 480 |
| 496 - 504 | 495 - 503 |
| 521 - 524 | 518 - 521 |
Вторая таблица с одинаковыми блоками в двух выравниваниях
| MAFFT | T-Coffee |
| 1 - 9 | 1 - 9 |
| 14 - 32 | 14 - 32 |
| 71 - 79 | 80 - 88 |
| 91 - 97 | 101 - 107 |
| 100 - 117 | 110 - 127 |
| 119 - 121 | 129 - 131 |
| 146 - 150 | 154 - 158 |
| 190 - 202 | 192 - 204 |
| 211 - 232 | 213 - 234 |
| 250 - 257 | 260 - 267 |
| 279 - 301 | 297 - 319 |
| 426 - 429 | 446 - 449 |
| 452 - 458 | 472 - 478 |
| 475 - 480 | 497 - 502 |
| 496 - 504 | 522 - 530 |
| 516 - 518 | 542 - 544 |
| 521 - 523 | 547 - 549 |
Также при сравнении выравниваний MAFFT и T-Coffee были найдены соотвествующие одинаковые колонки, не вошедшие в блоки: 84 и 93, 184 и 186, 511 и 537.
По результатам сравнения с помощью программы можно заметить, что у MAFFT и T-Coffee больше совпадающих блоков, нежели у MAFFT и MUSCLE. При этом, при использовании программы с опцией -p, позволяющей узнать процент, который составляют идентичные колонки для каждого из выравниваний была получена следующая информация: в сравнении MAFFT и MUSCLE у первого процент идентичных колонок составил 51.62% от всей длины, у второго - 51.92%; при сравнении же MAFFT и T-Coffee значения составили 53.33% и 50.82% соответственно. С опцией -l были получены длины выравниваний: MAFFT-525, T-Coffee-551, MUSCLE-522. Полученные проценты связаны с тем, что у T-Coffee длина выравнивания оказалась чуть-чуть больше двух других.
Еще можно заметить, что в двух сравнениях координаты некоторых блоков совпадают, что может свидетельствовать о том, что они действительно гомологичны. Блоки в ручном и программном сравнении также совпадают.
Для улучшения работы MAFFT и MUSCLE задейтвуют более сложное иттеративное рафинирование, однако T-Coffee использует консистентный подход, что делает его менее быстрым, но более точным. Можно сделать вывод, что T-Coffee лучше для работы с маленьким числом последовательностей, а для большого объема информации подойдет MAFFT как наиболее быстрый алгоритм.
Выравнивание по совмещению структур
Для выполнения задания было выбрано то же семейство PFAM - Asp, так как для него приведены структуры большого количества белков. Для совмещения были выбраны пепсин из Gadus Morhua с AC 1AM5, ризопуспепсин 1UH9 и рекомбинантный человеческий ренин 2REN. Все эти структуры состоят только из цепи A и имеют примерно одинаковую длину последовательности. При наложении 3D структур, можно увидеть, что лучше всего совпадают β-листы, в α-спиралях структуры значительно различаются, что связано с крупными различиями в функционировании данных белков в настолько разных организмах.

Структурное выравнивание было проведено в PDB с помощью функции Pairwise Structure Alignment. Выравнивания 1AM5 с 1UH9 и 1AM5 с 2REN были вручную подогнаны друг под друга. Получившееся выравнивание трех последовательностей я сравнила с помощью той же программы, что и выше, с выравниванием ClustalO. Совпавшие блоки выравниваний имеют одинаковые координаты и там, и там:
1: 4 - 10
2: 15 - 50
3: 53 - 80
4: 85 - 100
5: 103 - 107
6: 116 - 135
7: 139 - 164
8: 168 - 193
9: 196 - 214
10: 218 - 249
11: 252 - 258
12: 262 - 280
13: 291 - 297
14: 306 - 335
Процент идентичных колонок в обоих выравниваниях составил 83.93%. ClustalO хорош тем, что вместо попарных сравнений он использует подход с k-мерами, также его работа улучшается за счет алгоритма HHalign, который очень хорошо выявляет даже эволюционно далекие гомологи. Сравнение 3D структур дополнительно подтверждает гомологичность белков семейства.
Ссылка на 2 сравниваемых выравнивания: Проект в Jalview
ProbCons: Probabilistic consistency-based MSA
В множественном выравнивании последовательностей часто используются одна из популярных статистических моделей, такая как скрытая марковская модель. Скрытая марковская модель(HMM) — статистическая модель, задачей которой ставится разгадывание неизвестных параметров на основе наблюдаемых. HMM состоит из набора различных состояний, набора нормализованных вероятностей перехода из любого одного состояния в любое другое состояние (включая его самого) и набора нормализованных вероятностей того, что наблюдение происходит при заданном состоянии.
Одним из популярных методов с HMM является ProbCons, который использует функцию оценки, основанную на вероятностной согласованности.
Этапы работы алгоритма ProbCons:
1.Попарное вероятностное выравнивание - Для каждой пары последовательностей строится матрица совпадений на основе эволюционных моделей, к примеру BLOSSUM, после чего оценивается вероятность совпадений и несовпадений.
2.Построение матрицы достоверности - Для каждой позиции в выравнивании вычисляется вероятность того, что она корректна, таким образом выделяются наиболее надежные участки.
3.Построение направляющего дерева - Строится иерархическая кластеризация, дерево определяет порядок добавления последовательностей в множественное выравнивание.
4.Прогрессивное выравнивание - Последовательности добавляются по направляющему дереву, начиная с наиболее близких, на каждом шаге используется HMM-выравнивание с учетом вероятностных оценок.
5.Итеративное уточнение - Выравнивание улучшается за счет случайного разбиения на подгруппы и перевыравнивания, это повторяется до сходимости.
ProbCons подходит для анализа удаленных гомологов и обнаружения функциональных сайтов. Однако из-за сложности алгоритма, данная программа очень медленно работает.
Источники:
Chowdhury B, Garai G. A review on multiple sequence alignment from the perspective of genetic algorithm. Genomics. 2017 Oct;109(5-6):419-431. doi: 10.1016/j.ygeno.2017.06.007. Epub 2017 Jun 29. PMID: 28669847.
Do CB, Mahabhashyam MS, Brudno M, Batzoglou S. ProbCons: Probabilistic consistency-based multiple sequence alignment. Genome Res. 2005 Feb;15(2):330-40. doi: 10.1101/gr.2821705. PMID: 15687296; PMCID: PMC546535.