- Даны файлы:
- Координаты пептида, 2xl1.pdb.
- Файл с ячейкой уравновешеных молекул формамида, fam_em.gro
- Файл дополнительной топологии для формамида, fam.itp.
- Файл праметров для минимизации энергии em.mdp.
- Файл праметров для "утряски" воды pr.mdp.
- Файл праметров для молекулярной динамики md.mdp
- Построим файл топологии системы в силовом поле amber99sb и файл с координатами в формате Gromacs.
pdb2gmx -f 2xl1.pdb -o pep -p pep -ff amber99sb -water tip3p
Сделаем небольшой отступ в ячейке от ДНК.
editconf -f pep.gro -o pep_ec -d 1.5
Проведём оптимизацию геометрии системы, что бы удалить "плохие" контакты в молекуле.
grompp -f em -c pep_ec -p pep -o pep_em -maxwarn 1
mdrun -deffnm pep_em -v
Изменение максимальной силы в ходе оптимизации геометрии максимальная сила уменьшается (почти каждый раз на новом атоме), падая в итоге на 1 порядок: в начале
F-max = 4.37039e+03 (atom 146), в конце Maximum force = 3.2095328e+02 (atom 30). Оптимизировать о значения Fmax <1, как видно, не получилось.
- Добавим в ячейку молекулы формамида. Количество добавленных молекул формамида - 902.
genbox -cp pep_em -p pep -cs fam_em.gro -o pep_s
- Теперь надо изменить в текстовом редакторе файл тополгии pep.top. После строчки:
; Include forcefield parameters
добавим
#include "fam.itp"
; Include forcefield parameters
#include "fam.itp"
Добавим количество молекул формамида в запись [ molecules ]
1
стало:
[ molecules ]
; Compound #mols
Protein 1
FAM 902
- Нейтрализуем заряд системы. Это делаем в два шага: строим tpr и запускаем genion. В выводе grompp сказано, что заряд системы -1,
т. е. необходим 1 положительный ион для нейтрализации заряда системы (-np 1).
grompp -f em -p pep -c pep_s -maxwarn 1 -o pep_s
genion -s pep_s -o pep_si -p pep -np 1
- Проведём "утряску" формамида:
grompp -f pr -c pep_si -p pep -o pep_pr -maxwarn 1
mdrun -deffnm pep_pr -v
Переформатируем pep_pr.gro и pep_si.gro в pdb формат.
editconf -f pep_pr.gro -o
editconf -f pep_si.gro -o
Полученные файлы pep_pr.pdb и pep_si.pdb
Сравним визуально в PyMol изменеия в системах
 |
 |
| Молекулы растворителя упорядочены. |
После утряски. |
- Скопируем файлы на суперкомпьтер.
Запускаем тестовое моделирование на суперкомпьтере.
grompp -f md -c pep_pr -p pep -o pep_md -maxwarn 1
mpirun -np 16 -maxtime 5 -q test /home/golovin/progs/bin/mdrun_mpi -deffnm pep_md -v
Можно записать номер задачи и проверить ход счета в файле mdrun_mpi.out-....
При отсутствии ошибок переходим к основному моделированию.
Запускаем основное моделирование на суперкомпьтере.
mpirun -np 16 -maxtime 1200 /home/golovin/progs/bin/mdrun_mpi -deffnm pep_md -v
Анализ результатов.
Параметры моделирования
- Силовое поле используемое при построении топологии: amber99sb.
- Заряд системы: -1.
- Размер и форма ячейки: параллелепипед со сторонами (нм) 5.06500, 4.67000, 4.22100.
- Минимизация энергии:
- Алогритм минимизации энергии: l-bfgs
- Алгоритм расчёта электростатики и Ван-дер-Ваальсовых взаимодействий:
Coulomb cut-off; LJ or Bcukingham cut-off
- Модель, которой описывался растворитель: No
- Утряска растворителя:
- Параметр который обуславливает неподвижность биополимера: define = -DPOSRES
- Число шагов: 104.
- Длина шага: 1 фс.
- Алгоритм расчёта электростатики - pme, Ван-дер-Ваальсовых взаимодействий - Cut-off.
- Алгоритм термостата Berendsen, баростата - нет.
- Основной расчёт МД:
- Время моделирования: 7 часов 12 минут 42 секунды
количество процессоров: 16
эффективность масштабирования: 100%.
- Длина траектории: 20 нс.
- Число шагов: 10^7.
- Длина шага: 2 фс.
- Алгоритм интегратора: md
(Leap-frog).
- Алгоритм расчёта электростатики - pme, Ван-дер-Ваальсовых взаимодействий - Cut-off.
- Алгоритмы термостата v-rescale, баростата - Berendsen.
Визуальный анализ движений молекул
Использовалась команда:
trjconv -f pep_md.xtc -s pep_md.tpr -o pep_pbc_1.pdb -skip 20 -pbc mol
Полученный файл pep_pbc_1.pdb
К сожалению, молекула на экране передвигается по экрану, и анализировать что-то в таких
условиях трудно, поэтому применяем:
trjconv -f pep_md.xtc -s pep_md.tpr -o pep_fit_1.pdb -skip 20 -fit rot+trans
И получаем файл pep_fit_1.pdb
| Модель и время |
Изображение |
| Модель 0; t=0 |
 |
| Модель 3; t= 600 (Пептид начинает раскручиваться с С и N концов) |
 |
| Модель 5; t=1000 (Пептид изогнулся и с обоих концов раскрутился) |
 |
| Модель 6-12; t=1200-2400 (Пептид сворачивается обратно в альфа-спираль, но С-конец остается раскреченным) |
 |
| Модель 100 (конец); t=20000 (C-конец так и остался раскрученным) |
 |
Cредне-квадратичное отколнение
Так как у нас происходит конформационный переход, сначала рассчитаем отклонение
в ходе всей симуляции относительно стартовой структуры.
g_rms -f pep_md.xtc -s pep_md.tpr -o rms_1
Полученный файл rms_1.xvg
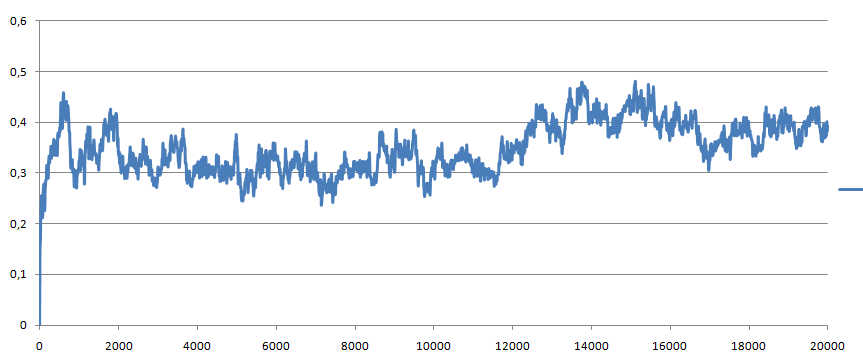- отклонение постепенно увеличивается примерно до 0.5, затем снова уменьшается до 0.45.
И относительно каждой предидущей структуры на растоянии 400 кадров.
Если ближе к концу закончился конформационный переход, то отколнение должно уменьшаться.
g_rms -f pep_md.xtc -s pep_md.tpr -o rms_2 -prev 400
Полученный файл rms_2.xvg
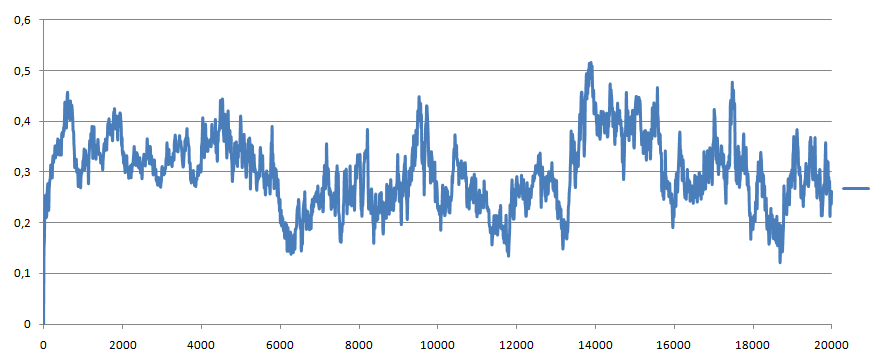- отклонение постепенно увеличивается и превышвет 0.5, затем уменьшается и колеблется 0.2-0.4.
Определите изменение гидрофобной и гидрофильной поверхности в ходе конформационного перехода.
g_sas -f pep_md.xtc -s pep_md.tpr -o sas_pep.xvg
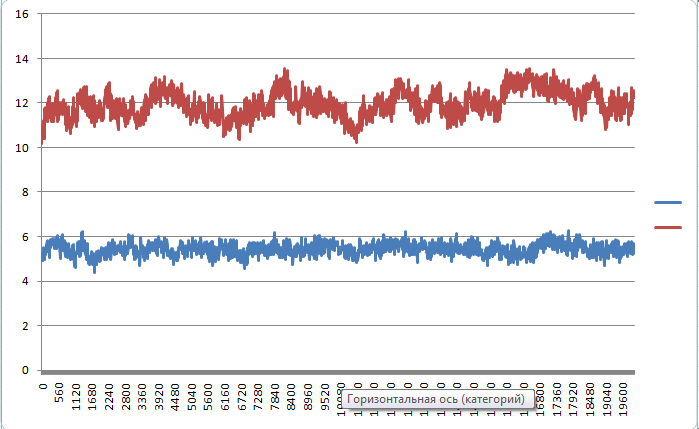
Красная-гидрофобная, синяя - гидрофильная.