Задание 3. Восстановление функции электронной плотности (ЭП)

Задание функции ЭП

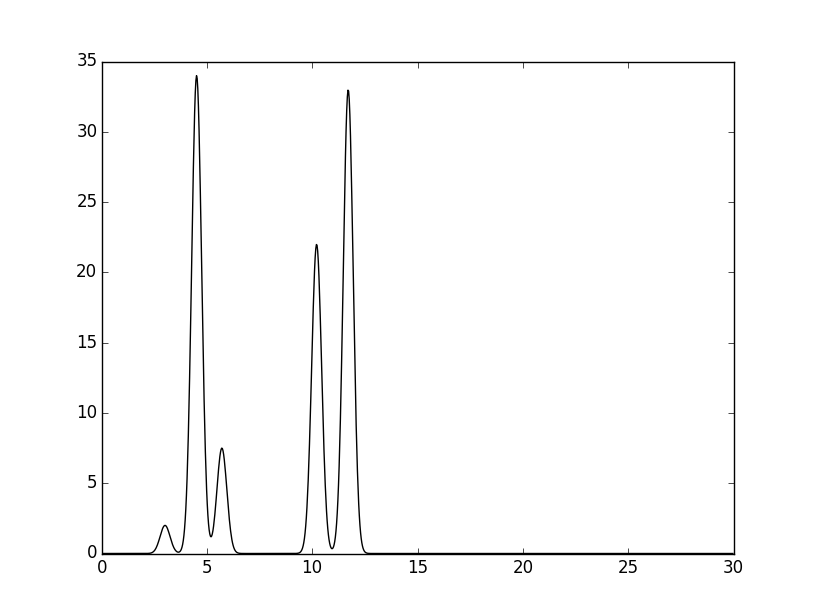
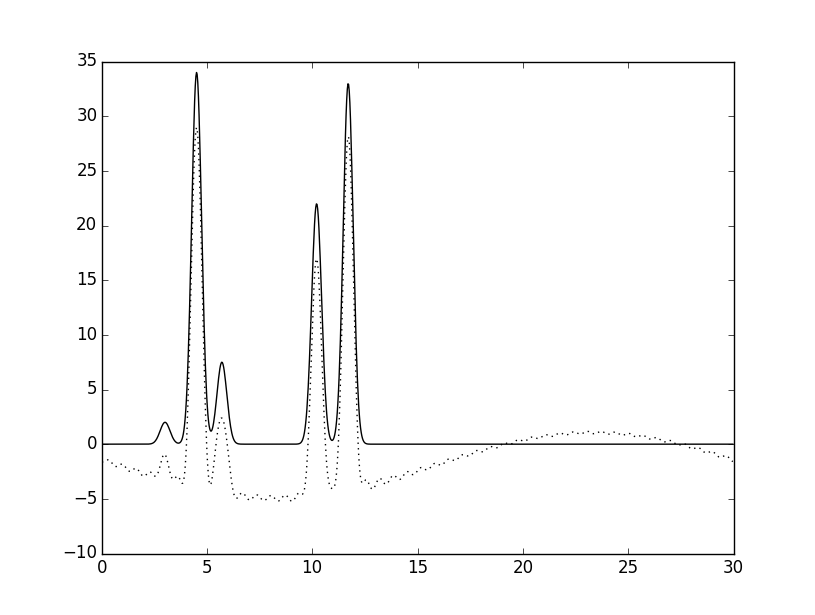
Модель для компьютерного эксперимента. На отрезке [0,30] (ангстремы) расположены две молекулы (3 + 2 атома). Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 A друг от друга. Молекулы расположены на расстоянии 4.5 A. Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме. Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py:

python compile-func.py -g 2,3,3+34,3,4.5+7.5,3,5.7+22,3,10.2+33,3,11.7

На выходе скрипта получаем текстовый файл func.txt, в котором заданы пары (Х,Y) функции. Так же скрипт выдает график функции ЭП, который приведен ниже.

Расчет амплитуд и фаз сигналов, моделирующих экспериаментальные данные был осуществлен с помощью скрипта func2fourier.py. Выходной формат скрипта имеет следующий вид:

 <номер гармоники>  <амплитуда>  <фаза>
 

Полный набор гармоник

Отбор гармоник

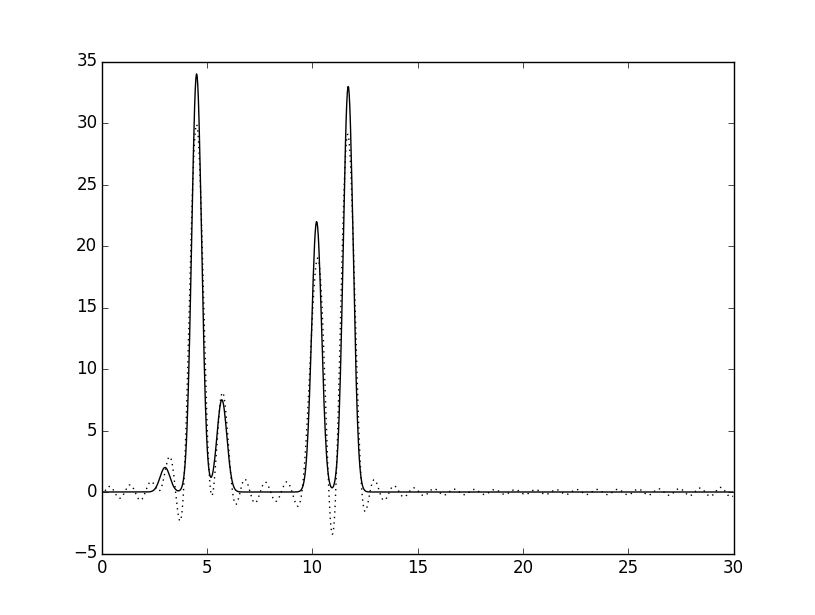
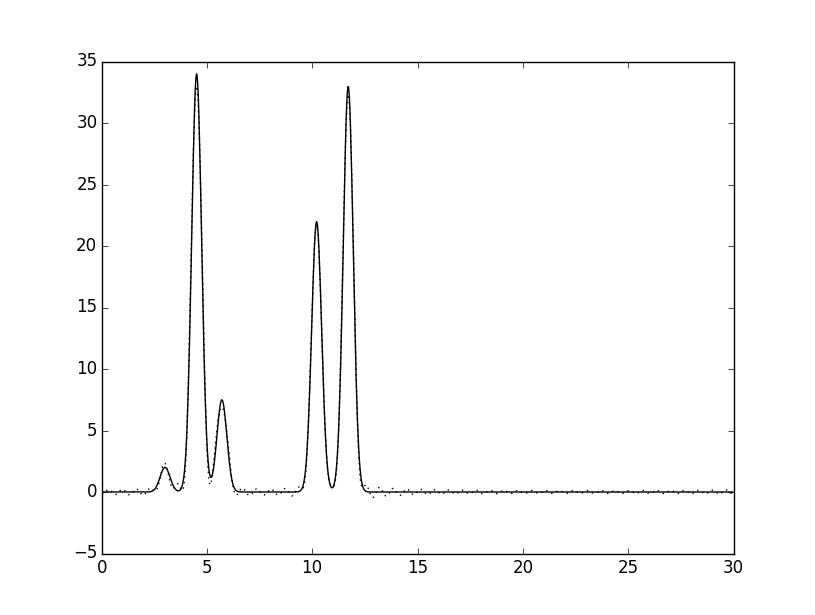
В первую очередь требовалось найти для 499 гармоник, полученных в предыдущем пункте, n0 - число гармоник, при котором восстановление отличное. Проверялись n0 =20, 30, 45. Ниже представлены графики, показывающие восстановленные функции электронной плотности. n0 было определенно равным 46.

n0=20	n0=20, без исходной функции плотности
n0=30	n0=30, без исходной функции плотности
n0=46	n0=46, без исходной функции плотности

Добавление шума

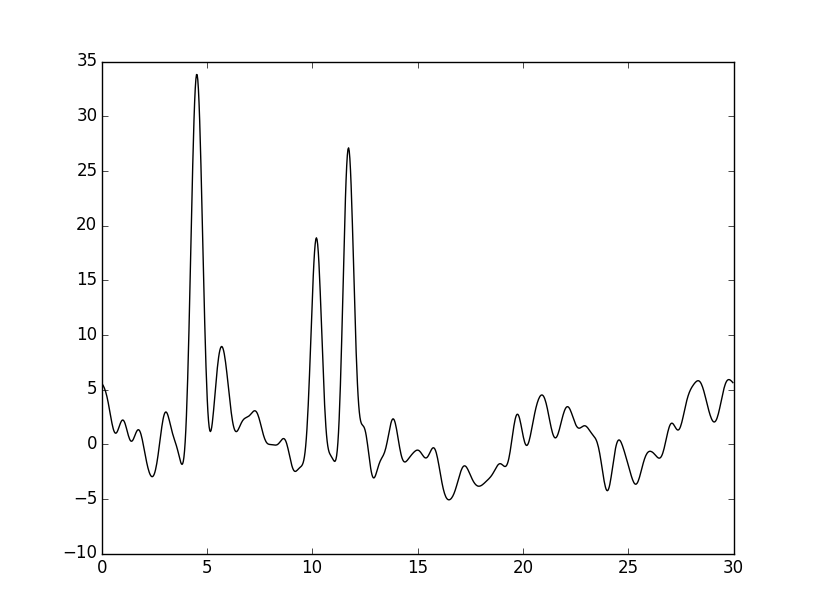
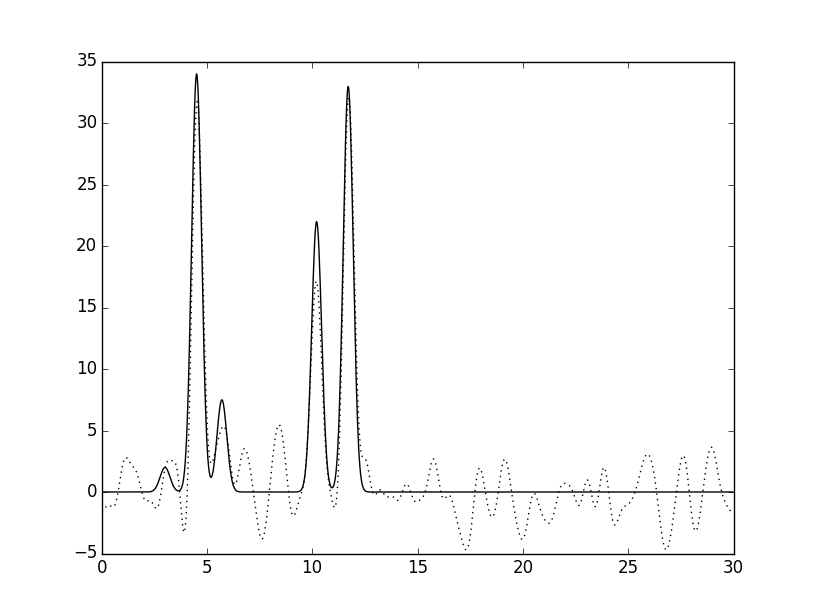
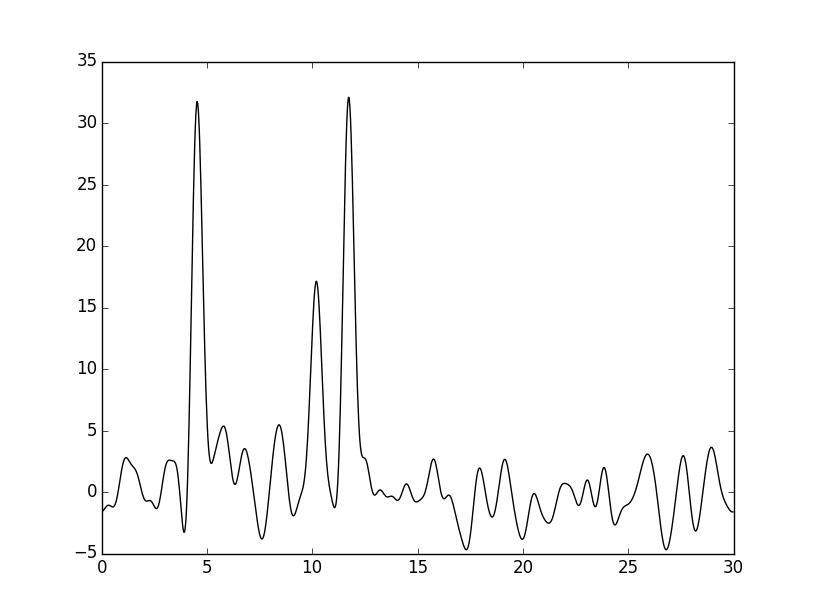
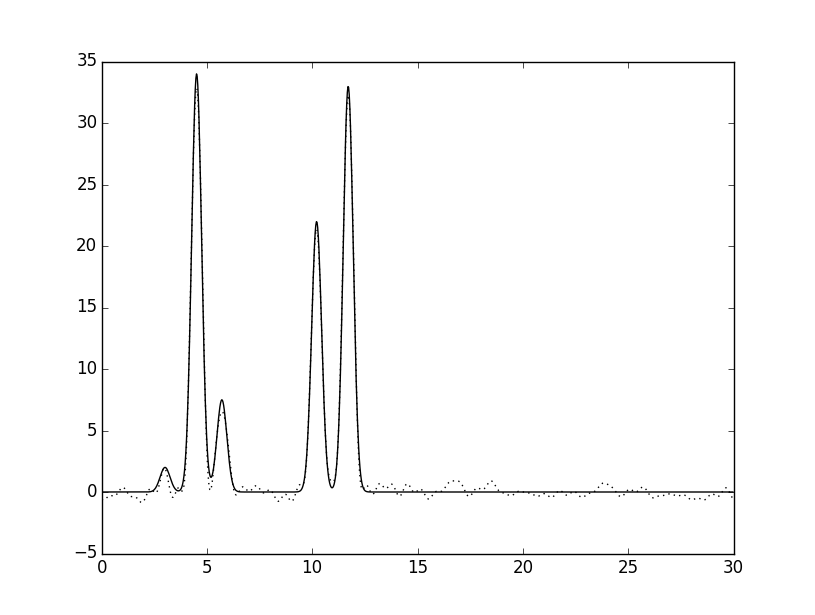
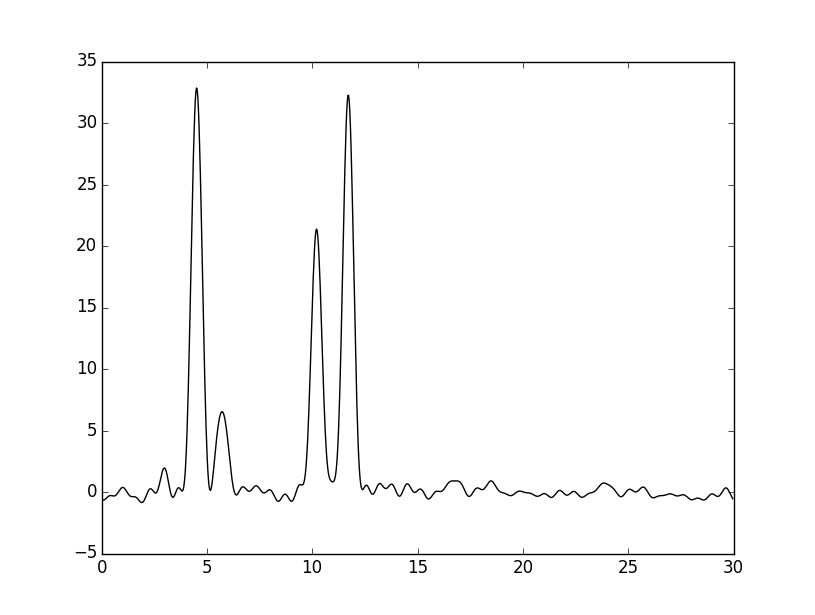
К амплитудам и фазам был добавлен шум (параметры -F и P скрипта func2fourier.py соответственно). Графики электронных плотностей, восстановленных по полному набору гармоник (n0=46) с шумом представлены ниже:

-P 20	-P 20, без исходной функции плотности
-F 20	-F20, без исходной функции плотности
-P 15, -F 15	-P 15, -F 15, без исходной функции плотности
-P 3, -F 3	-P 3, -F 3, без исходной функции плотности

Качество восстановления после добавления шума снизилось до среднего. При низких значениях шума (3% по фазе и амплитуде) восстановление отличное.

Неполный набор гармоник

Удаление начальных гармоник

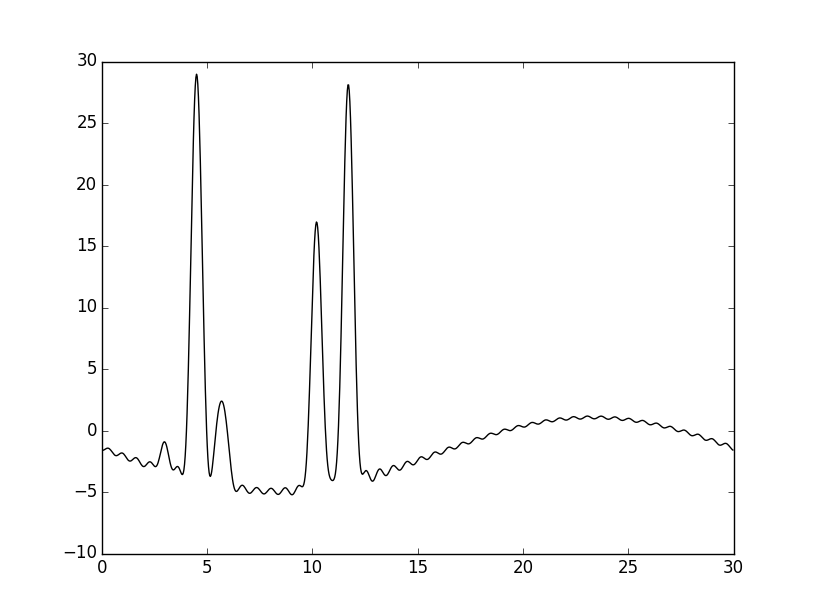
Для получения неполного набора гармоник удалили одну и две начальные гармоники.

Гармоники 1-45	Гармоники 1-45, без исходной функции плотности

Гармоники 2-45	Гармоники 2-45, без исходной функции плотности

В обоих случаях восстановление отличное, но при удалении двух гармоник функция заметно искажается.

Удаление гармоник из середины набора

Из набора удалили гармоники с номерами 24-26(5%) и 23-27(10%). Результат восстановления такого неполного набора гармоник представлен ниже.

Гармоники 0-23,27-45	Гармоники 0-23,27-45, без исходной функции плотности
Гармоники 0-24,28-45	Гармоники 0-24,28-45, без исходной функции плотности

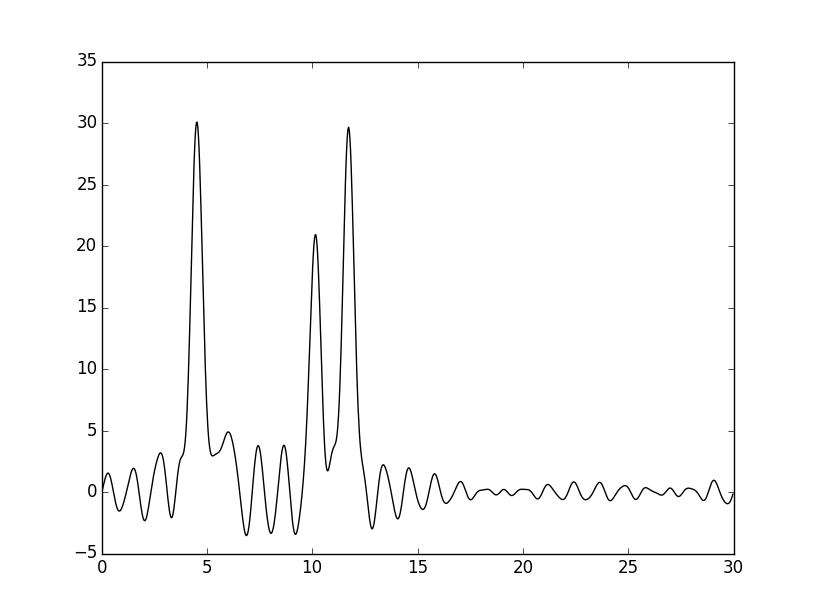В обоих случаях качество восстановления среднее.

Добавление гармоники с номером n0+10

К набору добавили гармонику с номером 55. Ниже представлен результат восстановления.

Гармоники 0-45,55	Гармоники 0-45,55, без исходной функции плотности

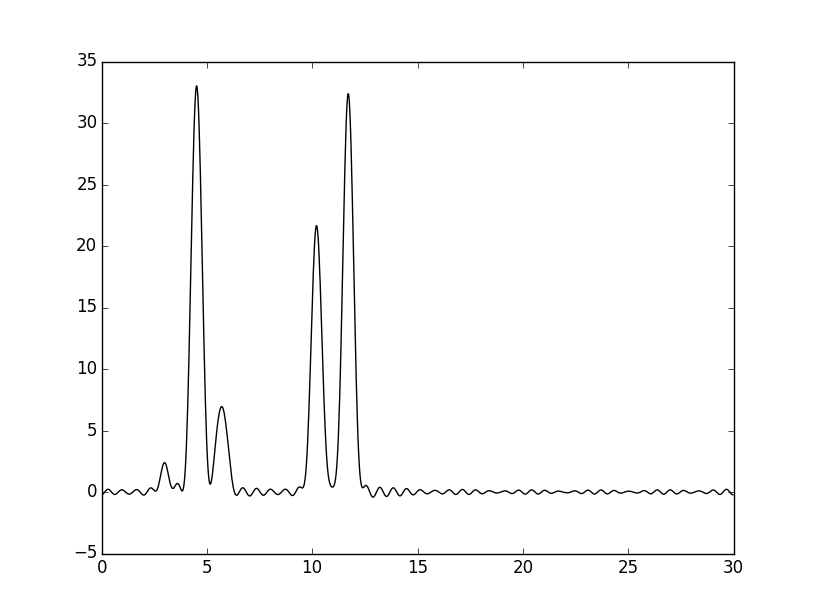Качество восстановления отличное, результат практически не отличается от того, что получается при восстановлении по полному набору гармоник.

По результатам анализа восстановления от исходных данных была заполнена таблица:

Набор гармоник	Разрешение, Å	Полнота данных, %	Шум амплитуды (% от величины F)	Шум фазы (% от величины P)	Качество восстановления
Полные наборы
0-20	1.5	100	0	0	Среднее
0-30	1	100	0	0	Хорошее
0-45	0.66	100	0	0	Отличное
0-45	0.66	100	0	20	Среднее
0-45	0.66	100	20	0	Среднее
0-45	0.66	100	15	15	Среднее
0-45	0.66	100	3	3	Отличное
Неполные наборы
1-45	0.66	97.8	0	0	Отличное
2-45	0.66	95.6	0	0	Отличное
0-23,27-45	0.66	93.5	0	0	Среднее
0-22,28-45	0.66	91.3	0	0	Среднее
0-45,55	0.54	100	0	0	Отличное