Восстановление функции электронной плотности

Задание функции ЭП

Для работы была выбрана модель из 2 молекул (5 атомов), показанная на рис.1. Молекулы имеют линейную форму и лежат на одной прямой. Молекулы находятся на расстоянии в 3 ангстрема, что соответствует длине возможной водродной связи можду двумя молекулами.

Рис.1. Модель взаимодействия двух молекул, используемая для построения функции электронной плотности. Под атомами подписана их координата по оси Х в ангстремах.

На основе данной модели была создана функция, описывающая электронную плотность гауссовыми кривыми, при помощи скрипта compile-func.py со следующими параметрами запуска:

Результат работы скрипта - файл func.txt c функцией ЭП данной модели на интервале [0,30] ангстрем. На рис.2 приведен график данной функции.

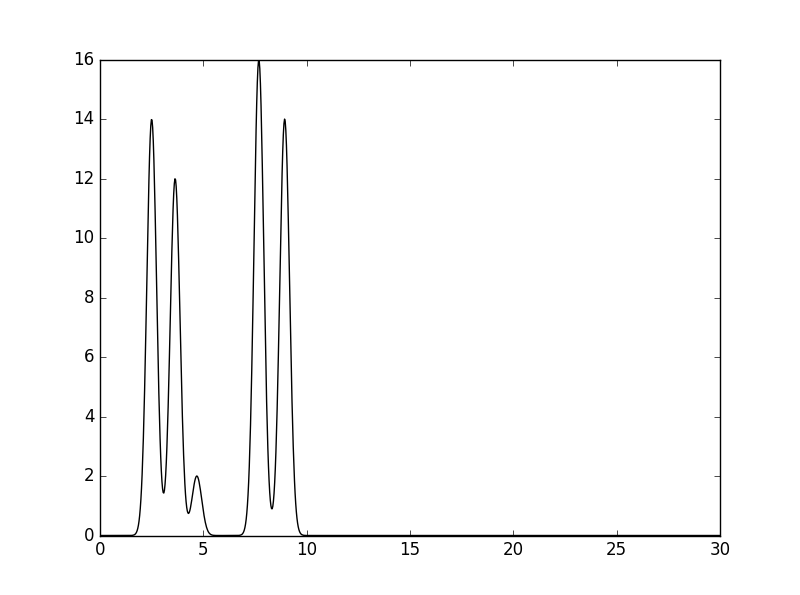
Рис.2. График электронной плотности.

Разложение ЭП в ряд Фурье

Полученное описание функции было использовано для её разложения на 499 гармоник на отрезке [0,30] при помощи скрипта func2fourier.py. Был получен файл calc_fourier.txt с коэффициентами Фурье, в котором для каждой гармоники записаны ее номер, амплитуда и фаза.

Восстановление функции электронной плотности по набору гармоник

По полному набору гармоник (все 499) с помощью скрипта fourier2func.py была восстановлена изначальная функция. Полученный график, показанный на рис.3А полностью совпадает с исходным.

Затем с помощью скрипта fourier-filter.py был определён порог числа гармоник, при котором функция восстанавливается отлично (по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции). Использовались наборы гармоник 0-5, 0-10, 0-15, 0-20, 0-25, 0-30, 0-33, 0-34, 0-35. Полученные графики показаны на рис.3Б-3К.

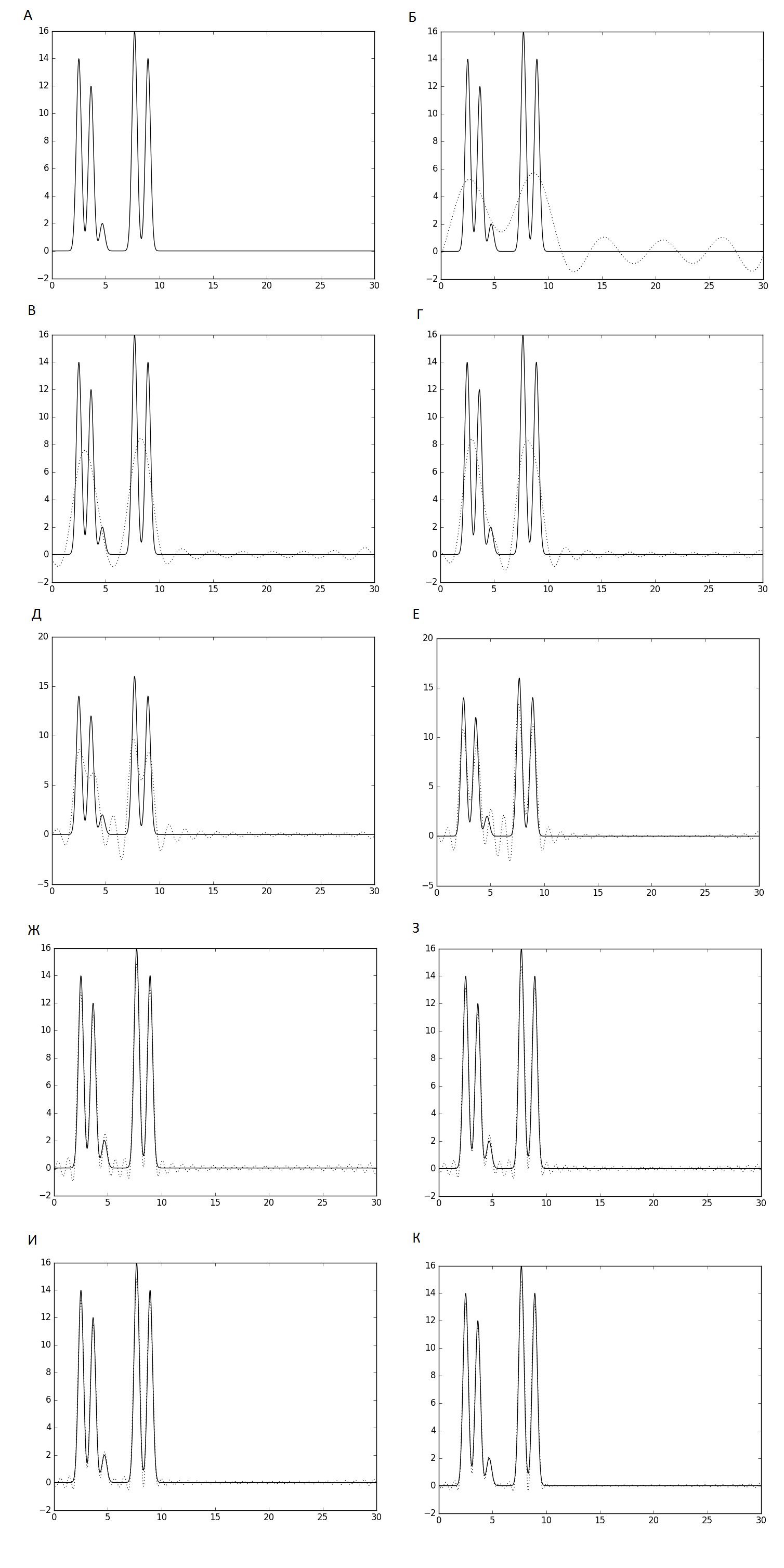
Рис.3. Восстановленные по различным наборам гармоник графики электронной плотности (пунктир), наложенные на исходный график. А - полный набор гармоник. Б - 0-5. В - 0-10. Г - 0-15. Д - 0-20. Е - 0-25. Ж - 0-30. З - 0-33. И - 0-34. К - 0-35.

Графики функций, восстановленных по гармоникам 0-5, 0-10 и 0-15 дают представление о расположении молекул, но отдельные атомы различить нельзя. Восстановление функции по гармоникам 0-20 все позволяет различить отдельные атомы в обеих молекулах. Восстановление функции по гармоникам 0-25 имеет пик для атома водорода, слабо отличимый от шума. Восстановление функции по гармоникам 0-30 позволяет различить все атомы в молекулах модели, но пик для атома водорода немного смещен. Восстановление функции по гармоникам 0-33 также имеет незначительное смещение пика атома водорода. При восстановлении по гармоникам 0-34 и 0-35 смещения нет, восстановление отличное. Следовательно, считаем, что n_0 в данном случае равно 34. Итак, для приближения моделирования к эксперименту число используемых гармоник уменьшено до 34.

Влияние шума на восстановление функции электронной плотности

Для добавления шума к амплитудам и/или фазам гармоник использовались опции -F и -P скипта func2fourier.py. Добавление шума приводит к тому, что к каждой амплитуде(F) или фазе (P) прибавляется случайное число, распределенное нормально с а = 0, σ = 0.2*F(или P). Использовались параметры F=10, F=50, P=10, P=50, F=10+P=10, F=50+P=50.

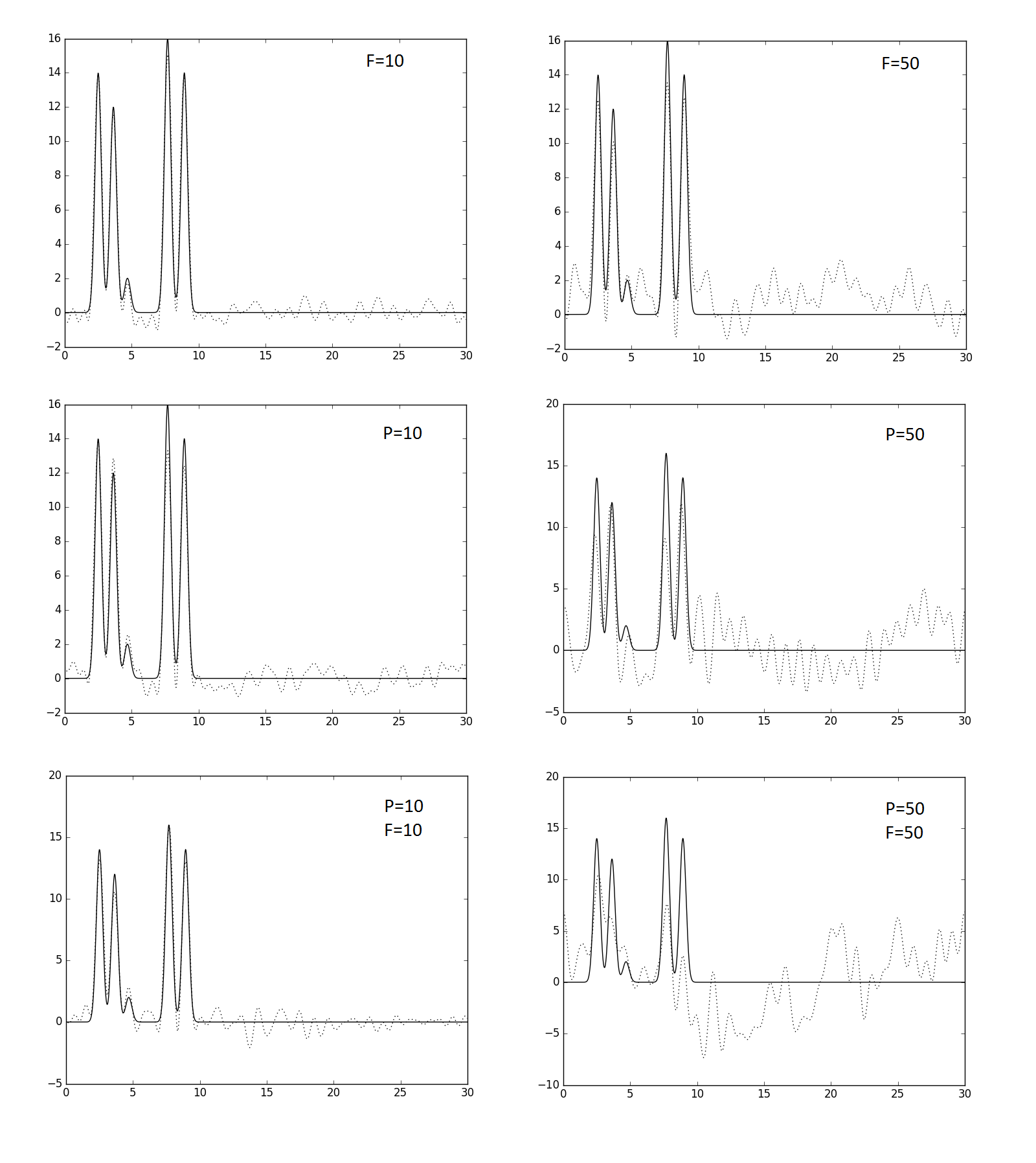
Рис.4. Графики восстановленных функций с разными уровнями шума (пунктир), наложенные на график исходной функции. Параметры наложенного шума указаны на графиках. Использовался набор гармоник 0-34.

При 10% уровне шума, наложенном на амплитуду, фазу или и то, и другое, сохраняется практически неизменным положение пиков атомов, все атомы различимы, кроме случая наложения шума на амплитуду - там отличить атом водорода от фона сложнее. При 50% уровне шума атом водорода теряется в фоне окончательно. Более тяжелые атомы сохраняются лучше, но 50% шум по фазе немного смещает их пики. 50% шум по фазе и амплитуде одновременно не позволяет в явном виде выделить даже положение молекул.

Неполные наборы гармоник

В реальности не всегда удаётся определить все гармоники, такой набор будет называться неполным. Чтобы сымитировать эту ситуацию в нашей модели мы будем удалять и добавлять гармоники в различных "частях" набора.

На рис.5 приведен результат удаления только первой и первой и второй гармоник из набора 0-34. Удаление гармоники номер 0 не изменяет форму функции значительно, только опускает график ниже оси ох. Удаление гармоник 0-1 приводит к появлению косинусоидной формы графика и приближению амплитуды пика атома водорода к фоновому шуму.

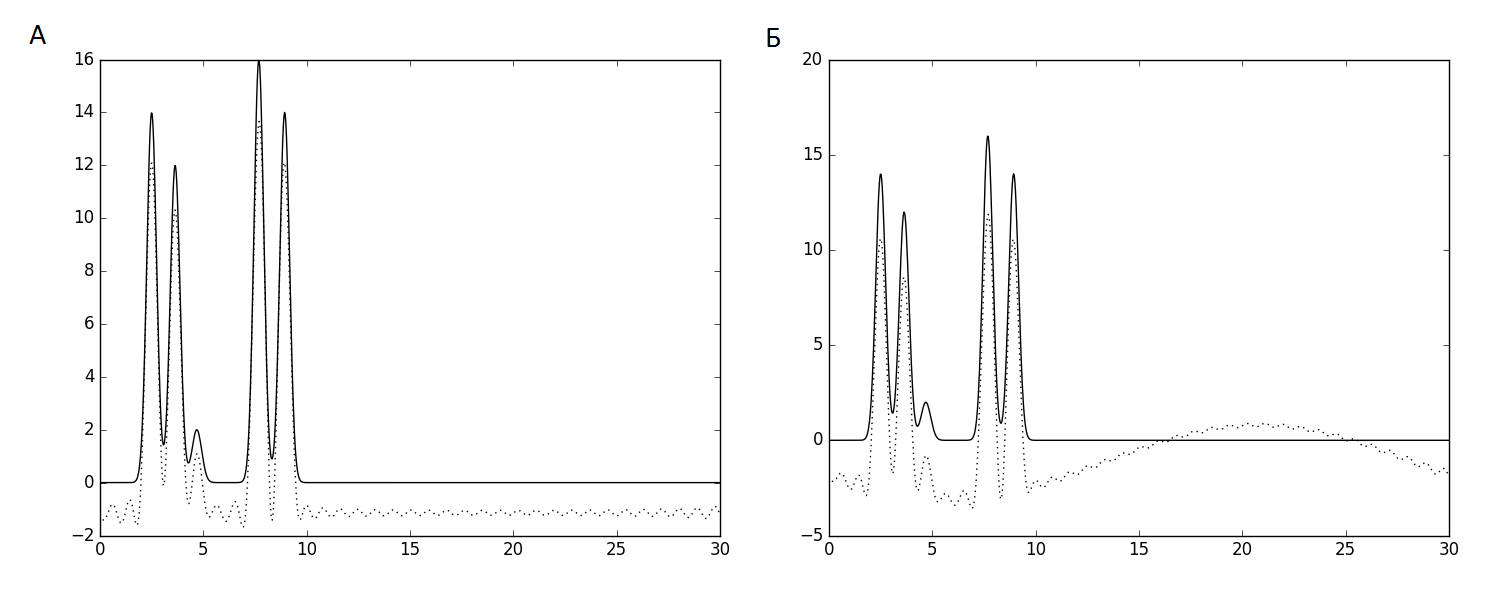
Рис.5. Восстановление функции ЭП из неполного набора гармоник (пунктир), наложенное на иходную функцию. А - набор гармоник 1-34. Б - набор гармоник 2-34.

Удалим теперь 3 гармоники из середины набора, возьмем набор гармоник 0-15,19-34. Результат восстановения функции по такому набору показан на рис.6. Как видно из рисунка, при удалении гармоник из середины набора становится сложнее различить атом водорода от фоновых пиков. Положение тяжелых атомов при этом иденифицируется точно.

Рис.6. Восстановление функции ЭП из неполного набора гармоник (пунктир), наложенное на иходную функцию. Набор гармоник 0-15,19-34.

Добавим к полному набору гармоник 0-34 гармонику 44. Результат восстановения функции по такому набору показан на рис.7. Как видно из рисунка, добавление гармоники с номером больше n_0 только уточняет восстановленную функцию.

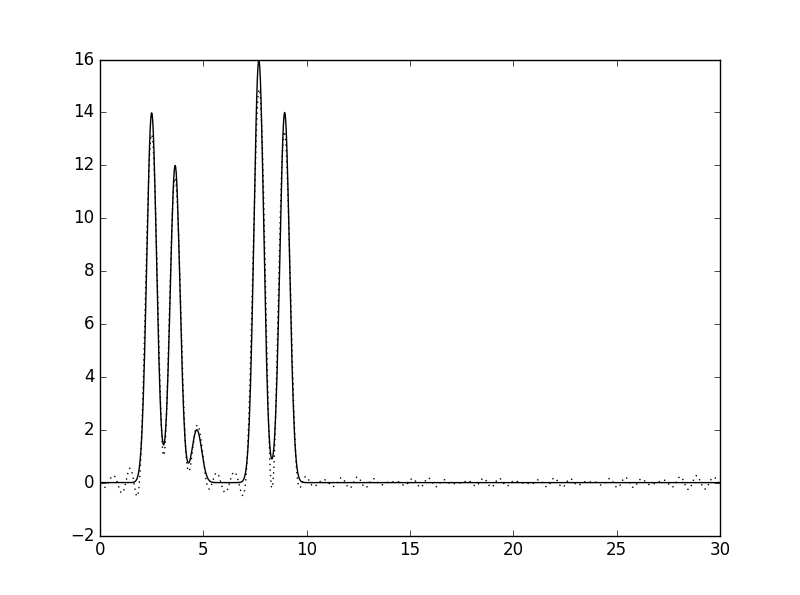
Рис.7. Восстановление функции ЭП из полного набора гармоник с добалением гармоники с высоким номером (пунктир), наложенное на иходную функцию. Набор гармоник 0-34,44.

Теперь смоделируем более-менее приближенную к реальности ситуацию: к неполному набору гармоник добавим 10% шум и к амплитудам, и к фазам. Были рассмотрены наборы гармоник 0-15,19-34 и 0-3,5-15,17,19-34. Результаты показаны на рис.8. В обоих случаях установить положение атома водорода затруднительно.

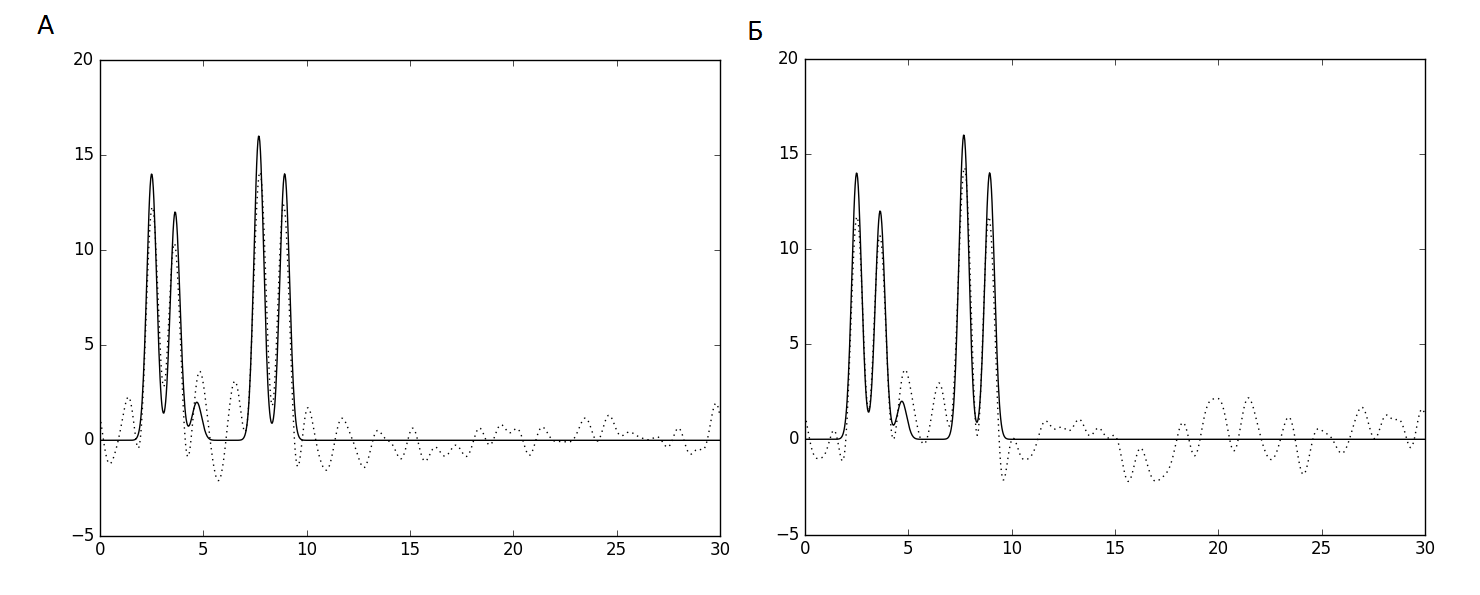
Рис.8. Восстановление функции ЭП из неполного набора гармоник с применением шума 10% по фазе и амплитуде (пунктир), наложенное на иходную функцию. А - набор гармоник 0-15,19-34, Б - 0-3,5-15,17,19-34.

Разрешение полученных графиков функции электронной плотности

Разрешением полного набора гармоник называется период гармоники с номером n, т.е. с наибольшим номером. Период гармоники равен расстоянию между соседними максимумами синусоиды. Период гармоники с номером n определяется как T/n, где T - длина рассматриваемого отрезка (в нашем случае - 30). Таким образом, разрешение полного набора гармоник рассчитывается как d0 = T/n.

Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо сообщить полноту данных — процент гармоник с длиной волны большей d от максимально возможного, присутствующих в наборе. Для полного набора данных (разрешение d=T/n) полнота равна 100%. Таким образом для неполного набора гармоник можно ввести поправку на полноту набора: d = d0/m, где m - полнота набора.

Выводы

Таким образом, факторами, влияющими на качество восстановления фукции по гармоникам являются полнота данных и наличие шума. Влияние небольших уровней шума меньше, чем влияние отсутствующих гармоник. Наибольшее влияние шума и неполноты данных оказывается на легкие атомы (атом водорода). Положение более тяжелых атомов определить проще.

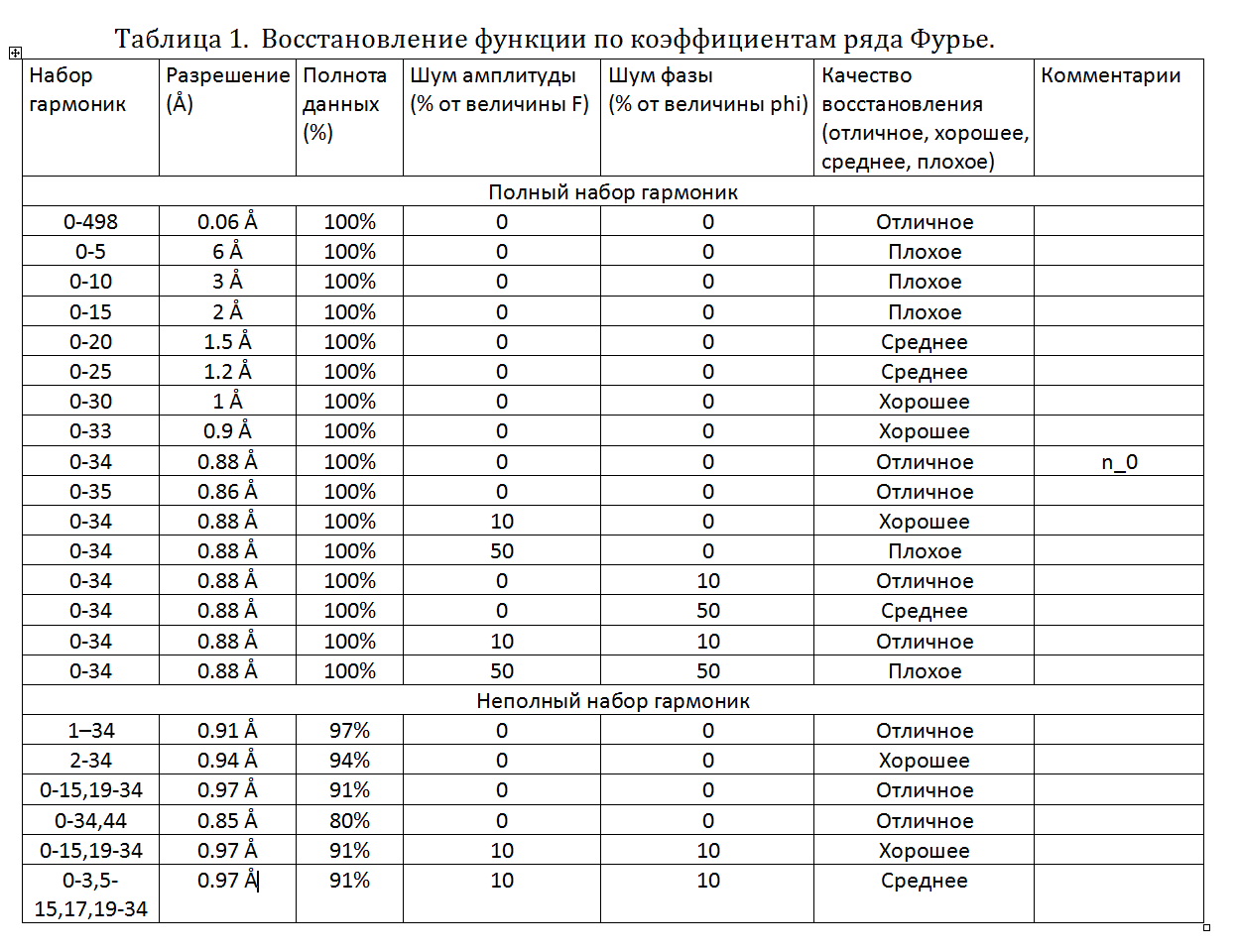
В таблице 1 приведены полные результаты восстановления функции по различным наборам гармоник.